【C++习题】17.二分查找算法_二分查找

---

二分查找算法简介

1. 特点：

   二分查找算法，是最恶心，细节最多，最容易写出死循环的算法。（而且非常难调试）

   不过如果真的掌握了二分算法后，会觉得这个是最简单的算法。

2. 学习中的侧重点：

• 算法原理：

  一开始会觉得只有数组有序的情况才能使用二分算法

  但是学到后面，会发现就算无序，只要有规律也可以使用二分算法

• 模板：

  不要死记硬背，需要理解背后的原理，做到理解后再记忆。

• 会讲3个模板

  1. 朴素的二分模板
  2. 查找左边界的二分模板
  3. 查找右边界的二分模板

  3个模板加起来不超过20行，可以解决 99.99%的二分题，但不能只背模板。

下面的一题会讲到第一个模板，后一题会讲第二第三个模板。

朴素的二分模板，朴素意味着简单，只有一些非常简单的二分题才用到。

查找左边界的二分模板和查找右边界的二分模板是万能的，也就是朴素模板可以解决的也可以用另外两个解决，不过细节很多。

---

题目链接：

leetcode 704.二分查找

---

题目描述：

---

解法

暴力解法：

遍历一遍，时间复杂度O(n)

例如：[1，2，3，4，5，6，7，8]，t=5

比如4，4比t小，那么它前面的比4还小，那么全比t小，可以把4和4之前的数全干掉。

同理，6和6后面的数也一样可以干掉。

总的来说就是，随便找个端点，只要不是目标值，那么它的一侧可以全部干掉。

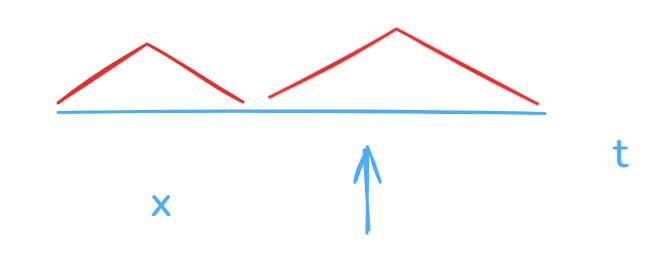
总结来说就是：二段性

就是当我们发现一个规律，然后根据这个规律选取某一个点能把这个数组分成两部分，然后根据规律可以有选择的舍去一部分，进而在另一部分里面继续查找的时候，就可以使用二分查找算法。

注意上面的描述，不管有序无序，只要有二段性都可以使用二分算法。

对于端点的选择，我们可以选择1/2处，1/3处，1/4处等等。我们的目的是找到二段性。

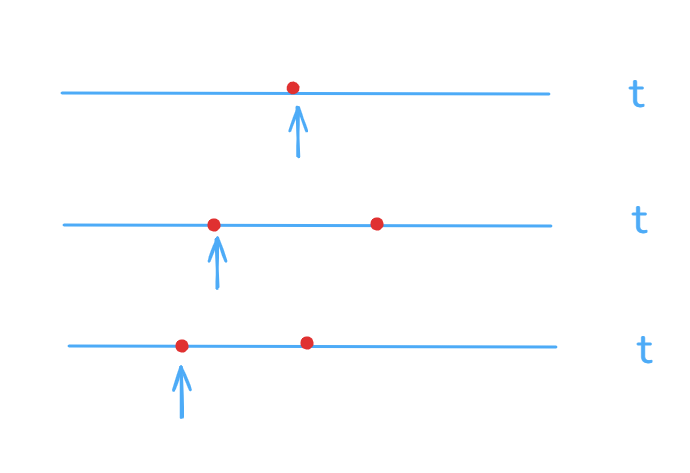
所以端点的选择比较多，但是我们一般选1/2的点。在概率学里面是求数学期望。

就像1/3处的点，虽然可能直接把2/3的部分抹除，但是也可能只抹除了1/3。

在这么多的端点的划分里面，选择中间这个点的时间复杂度是最好的。

我们可以定义一个left指针，right指针和mid指针

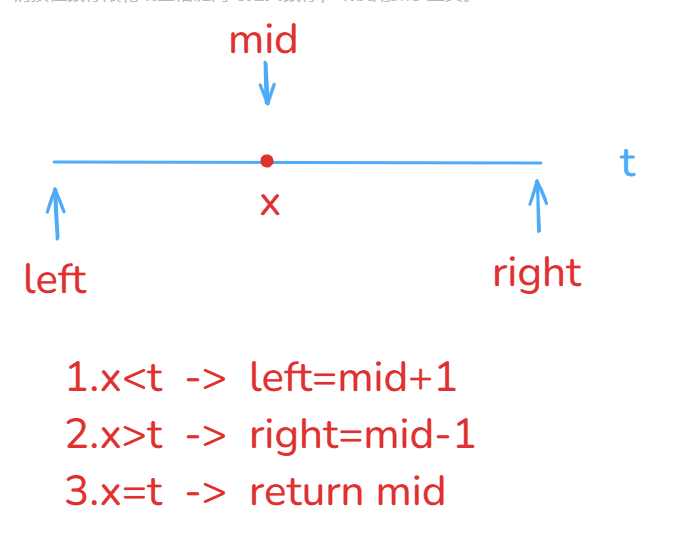
这3步就是朴素二分算法的核心了。

细节问题：

1. 循环结束的条件是什么？

   left>right的时候结束循环

   left<=right的时候一直循环

2. 为什么是正确的？

   通过二段性达到和暴力解法一样的排除作用

3. 为什么时间复杂度快？

   log₂n

---

C 算法代码：

int search(int* nums, int numsSize, int target)
{// 初始化 left 与 right 指针int left = 0, right = numsSize - 1;// 由于两个指针相交时，当前元素还未判断，因此需要取等号while (left <= right){// 先找到区间的中间元素int mid = left + (right - left) / 2;// 分三种情况讨论if (nums[mid] == target) return mid;else if (nums[mid] > target) right = mid - 1;else left = mid + 1;}// 如果程序走到这里，说明没有找到目标值，返回 -1return -1;
}

---

图解

例如：[1，2，3，4，5，6，7，8]，t=5

1. left = 0, right =7

   left <= right进入循环

   mid=0+(7-0)/2=3

   

   nums[mid]=4<t

   满足else条件，执行left = mid + 1=4

2. left = 4, right =7

   left <= right进入循环

   mid=4+(7-4)/2=5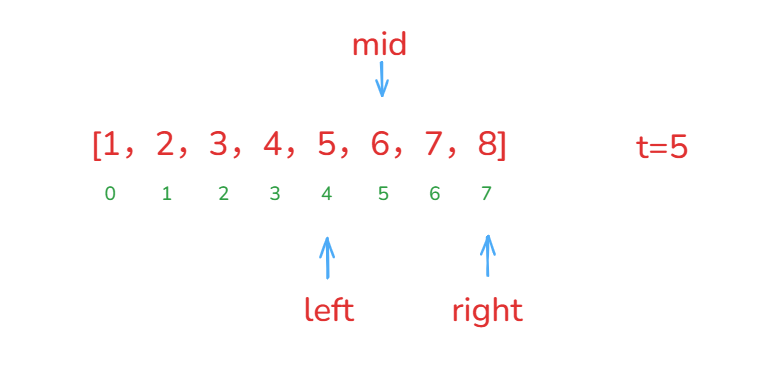

   

   nums[mid]=6>t

   满足nums[mid] > target条件，执行right = mid - 1=4

3. left = 4, right =4

   left <= right进入循环

   mid=4+(4-4)/2=4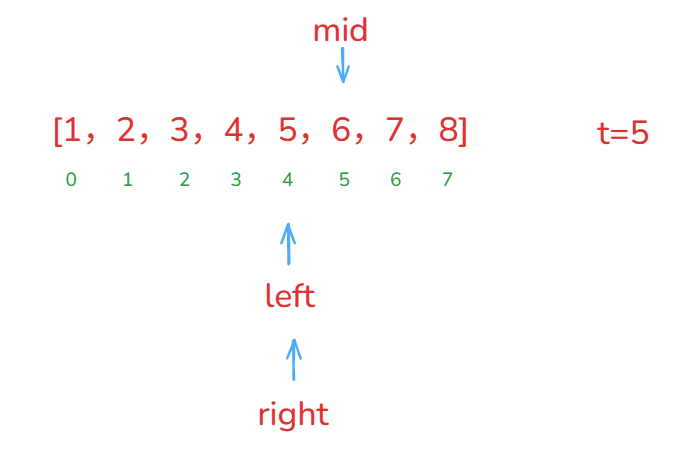

   

   满足nums[mid] == target)条件，执行return mid;

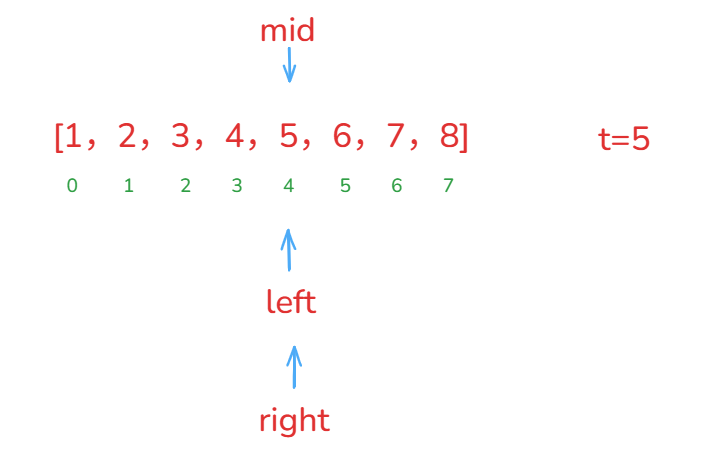
4. 程序结束。

---

总结朴素二分模板

while(left <= right){int mid = left + (right - left) / 2;//int mid = left + (right - left + 1) / 2;//这两个在朴素版本作用一样if(......)left = mid + 1;else if(......)right = mid - 1;elsereturn ......;
}