当前位置： 首页 > news >正文

微信小程序 本地调试和vconsole可以 但在体验上页面不请求数据

news 2026/2/9 15:14:19

微信小程序页面不请求数据

本地调试和vconsole可以 但在体验版页面不请求数据，如遇到这类问题基本都是一样的解决办法

1、如何调试找到问题

首先要把小程序本地设置的不校验合法域名关掉，不然本地一直都是好的
在这里插入图片描述

然后通过本地真机调试打断点找到问题位置

我的问题是wx.downloadfile这个方法请求失败，失败代码如下

在这里插入图片描述

2. 问题找到了就好解决了，需要在小程序开发管理中配置域名

登录小程序公众平台 -> 开发管理 -> 开发设置（往下滑）-> 服务器域名 配置一下域名（注意区分https/http） 例如：https://mp.weixin.qq.com
配置完等一会，重启一下微信开发者工具就好了
在这里插入图片描述
在这里插入图片描述

在这里插入图片描述

关注博主更多文章 https://blog.csdn.net/qq_39882537

相关文章：

微信小程序 本地调试和vconsole可以 但在体验上页面不请求数据

微信小程序页面不请求数据 本地调试和vconsole可以 但在体验版页面不请求数据，如遇到这类问题基本都是一样的解决办法 1、如何调试找到问题 首先要把小程序本地设置的不校验合法域名关掉，不然本地一直都是好的 然后通过本地真机调试打断点找到问题位…...

编程日记 2024/12/3 9:53:43

QT：将QTableWidget内容写入txt文件中

文章详请：最近在做手在眼上的标定，首先要采集机械臂数据和图像数据，我使用tablewidget进行机械臂数据的显示，最后的计算需要将机械臂位姿数据存储在txt文件中。 引用：Qt如何保存tableWidget数据？_qt table…...

编程日记 2024/12/3 9:52:42

前端面试题(六)

1.let,var,const区别 1.作用域： 　var：var声明的变量存在函数作用域或全局作用域，这意味着它们在声明它们的函数内部可见，而不在块级作用域内可见。 let和const：let和const声明的变量存在块级作用域，这…...

编程日记 2024/12/3 9:51:40

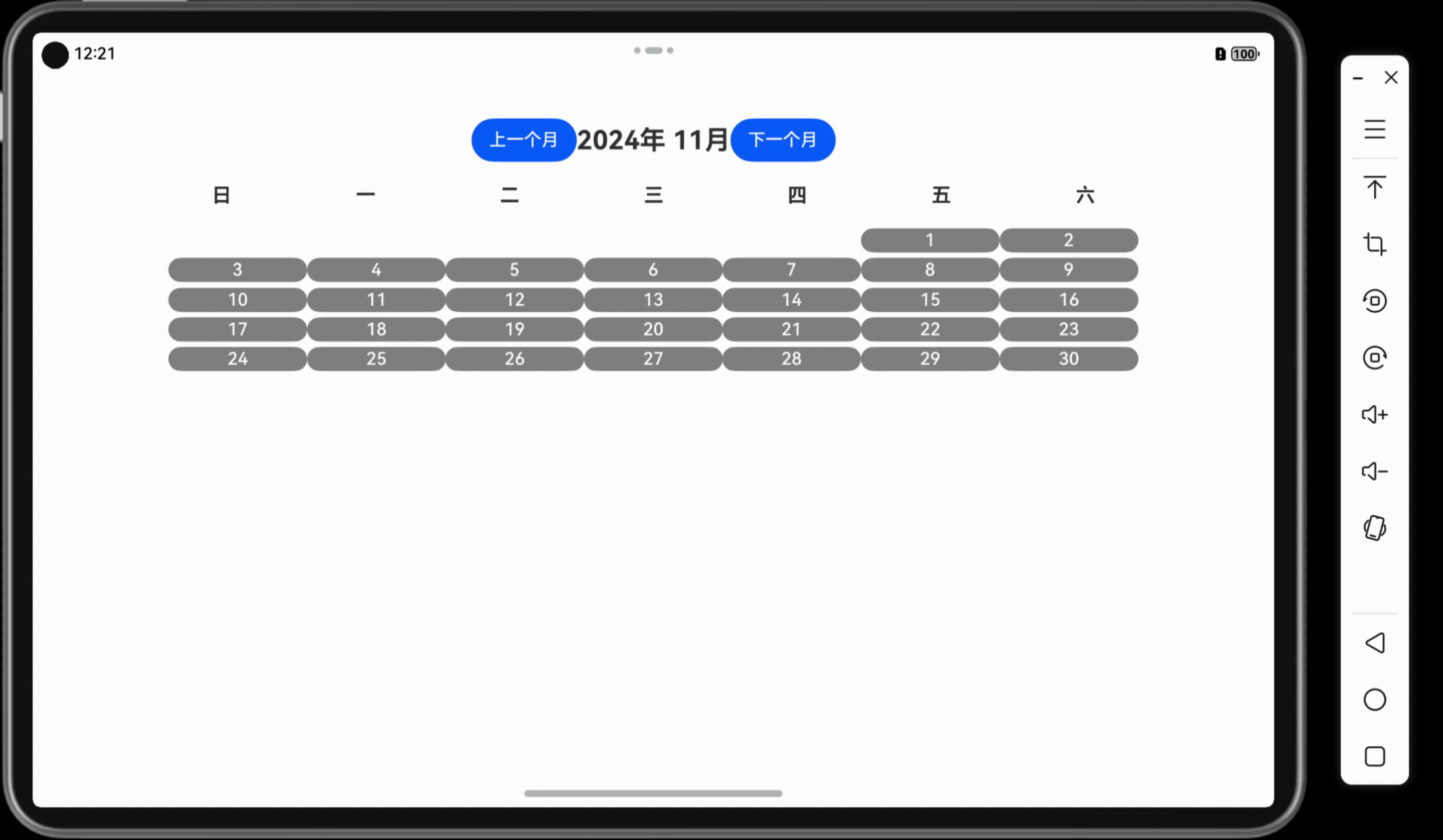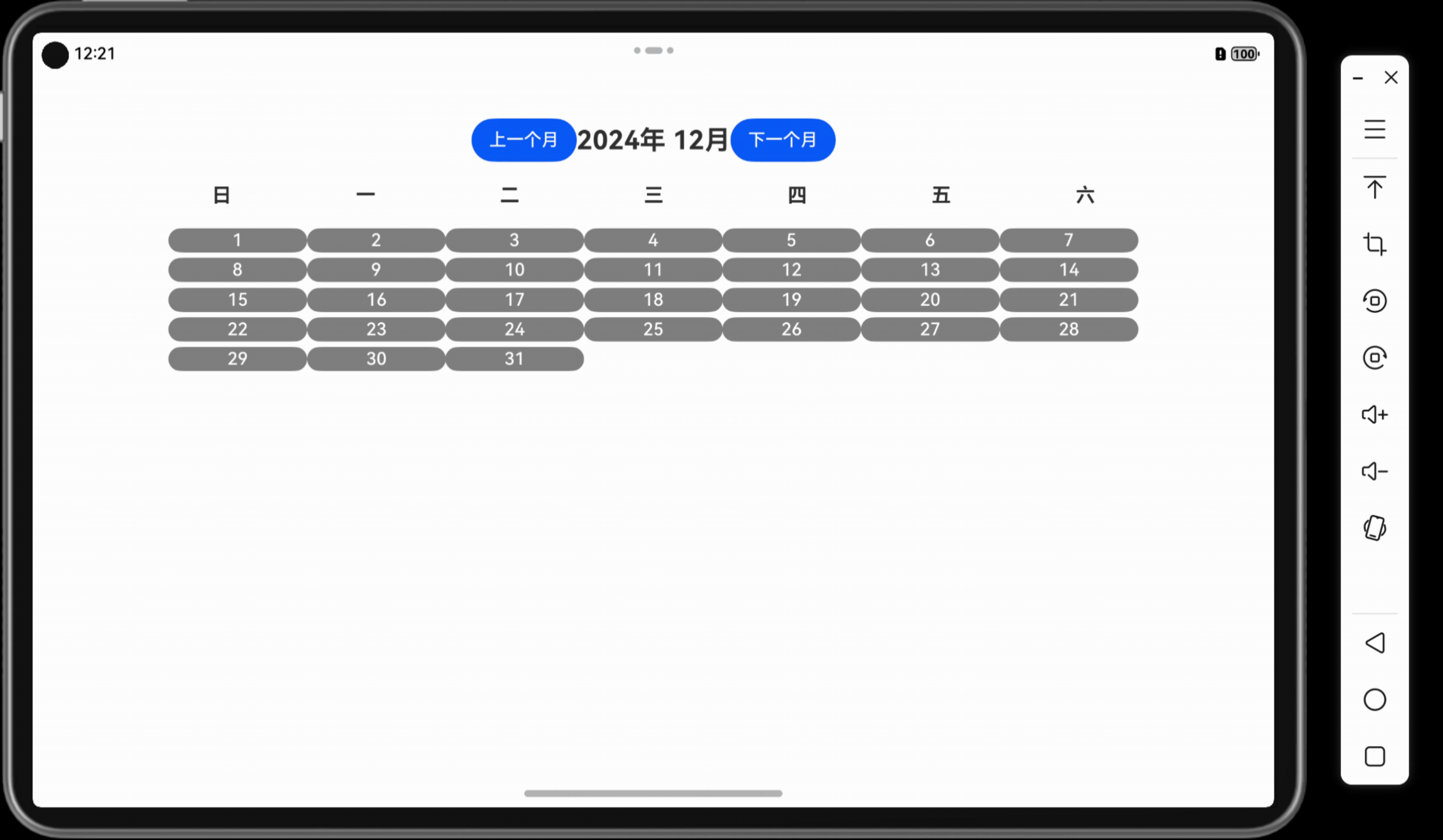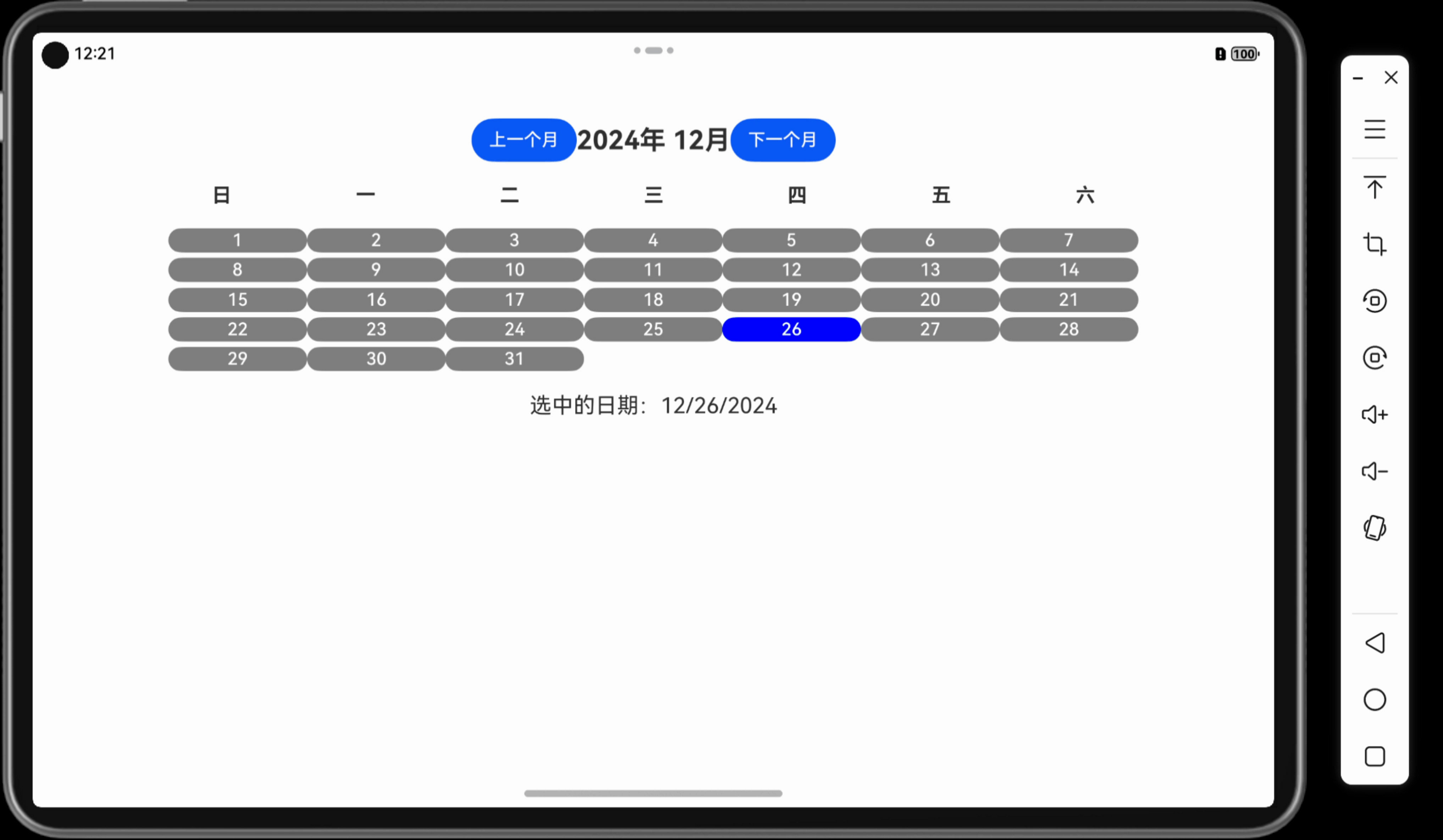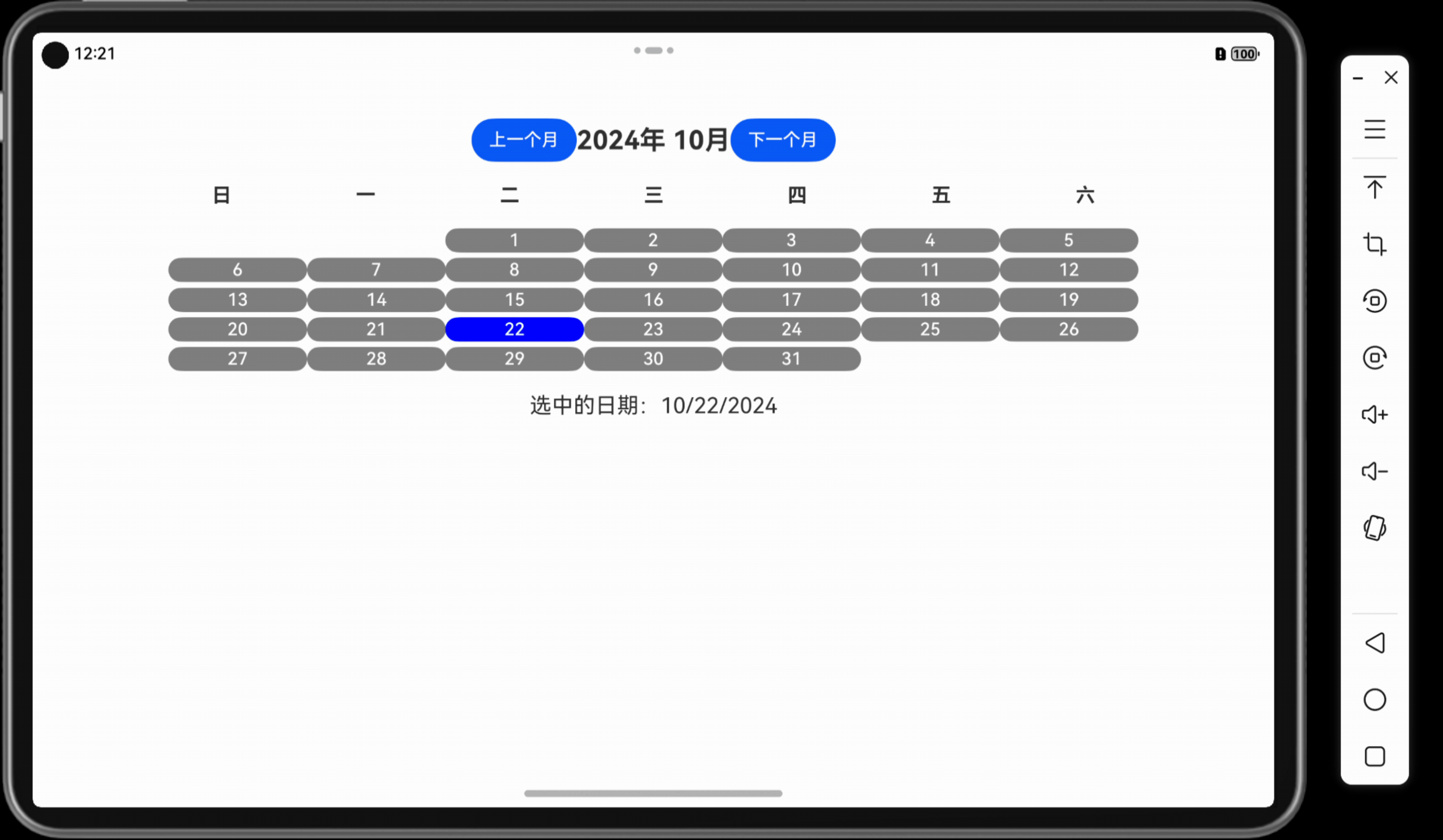
「Mac畅玩鸿蒙与硬件35」UI互动应用篇12 - 简易日历

本篇将带你实现一个简易日历应用，显示当前月份的日期，并支持选择特定日期的功能。用户可以通过点击日期高亮选中，还可以切换上下月份，体验动态界面的交互效果。 关键词 UI互动应用简易日历动态界面状态管理用户交互 一、功能说明…...

编程日记 2024/12/3 9:50:39

Leetcode581. 最短无序连续子数组(HOT100)

链接 我的代码&#xff1a; class Solution { public:int findUnsortedSubarray(vector<int>& nums) {vector<int> res nums;sort(res.begin(),res.end());int l 0,r nums.size()-1;while(nums[l]res[l]){l;if(lnums.size()){return 0;}}while(nums[r]res…...

编程日记 2024/12/3 9:49:37

HTML前端开发-- Flex布局详解及实战

引言 Flex布局&#xff0c;全称为Flexible Box Layout&#xff0c;是一种现代CSS布局技术&#xff0c;它提供了一种更有效的方式来设计响应式布局和复杂页面布局。本文将详细介绍Flex布局的基本概念、属性以及实战应用。 一、基本概念 Flex布局的核心是Flex容器&#xff08;…...

编程日记 2024/12/3 9:47:35

基于JWT跨语言开发分布式业务系统的挑战与实践：多语言协作的最佳方案

在现代分布式架构下&#xff0c;开发团队往往由来自不同技术栈和开发语言的工程师组成。如何有效地管理这些开发人员的协作&#xff0c;尤其是在实现跨语言的认证与授权机制时&#xff0c;成为了开发者面临的一个重大挑战。JSON Web Token&#xff08;JWT&#xff09;作为一种轻…...

编程日记 2024/12/3 9:44:31

二分法篇——于上下边界的扭转压缩间，窥见正解辉映之光（2）

前言 上篇介绍了二分法的相关原理并结合具体题目进行讲解运用&#xff0c;本篇将加大难度&#xff0c;进一步强化对二分法的掌握。 一. 寻找峰值 1.1 题目链接&#xff1a;https://leetcode.cn/problems/find-peak-element/description/ 1.2 题目分析: 题目要求返回数组内…...

编程日记 2024/12/3 9:42:28

什么是 Kata Containers？

什么是 Kata Containers&#xff1f; Kata Containers 是一种结合了容器技术和虚拟机技术的轻量级运行时&#xff0c;旨在提供容器的速度和虚拟机的安全性。它将容器运行在一个隔离的虚拟机中&#xff0c;从而大幅提升安全性&#xff0c;同时保持容器的高效性。 Kata Contain…...

编程日记 2024/12/3 9:40:25

SpringMvc项目配置RabbitMq

前言&#xff1a;只有消费者部分&#xff0c;没有记录生产者部分 结构图 配置类 可以xml配置&#xff0c;也可以配置类&#xff0c;二者可以相互转化。两种bean注入的方式。 import org.springframework.amqp.rabbit.connection.CachingConnectionFactory; import org.spring…...

编程日记 2024/12/3 9:36:20

shell编程（4）脚本与用户交互以及if条件判断

shell编程&#xff08;4&#xff09;脚本与用户交互以及if条件判断 声明&#xff01; 学习视频来自B站up主 ​泷羽sec​​ 有兴趣的师傅可以关注一下&#xff0c;如涉及侵权马上删除文章 笔记只是方便各位师傅的学习和探讨&#xff0c;文章所提到的网站以及内容&#xff0c;…...

编程日记 2024/12/3 9:34:17

vue2组件跨层级数据共享provide 和 inject

在 Vue 2 中&#xff0c;provide 和 inject 的功能也是可以使用的&#xff0c;虽然在 Vue 3 中它们成为了组合式 API 的一部分。在 Vue 2 中&#xff0c;provide 和 inject 主要是用于祖先组件和后代组件之间的数据共享&#xff0c;而不是通过 props 和 emit 逐层传递。 Vue 2…...

编程日记 2024/12/3 9:33:16

springboot/ssm校园闲置物品交易系统ava大学生二手闲置交易平台web二手源码

springboot/ssm校园闲置物品交易系统ava大学生二手闲置交易平台web二手源码 基于springboot(可改ssm)htmlvue项目 开发语言&#xff1a;Java 框架&#xff1a;springboot/可改ssm vue JDK版本&#xff1a;JDK1.8&#xff08;或11&#xff09; 服务器&#xff1a;tomcat 数…...

编程日记 2024/12/3 9:32:15

Redis实现限量优惠券的秒杀

核心&#xff1a;避免超卖问题&#xff0c;保证一人一单 业务逻辑 代码步骤分析 全部代码 Service public class VoucherOrderServiceImpl extends ServiceImpl<VoucherOrderMapper, VoucherOrder> implements IVoucherOrderService {Resourceprivate ISeckillVoucher…...

编程日记 2024/12/3 9:26:07

Linux centOS 7 安装 rabbitMQ

1.安装前需要了解&#xff0c;rabbitmq安装需要先安装erlang&#xff0c;特别注意的是erlang与rabbitmq的版本之间需要匹配。 el/7/rabbitmq-server-3.10.0-1.el7.noarch.rpm - rabbitmq/rabbitmq-server packagecloud 3.10版本的rabbitmq 对于erlang的版本要求可以看此连接…...

编程日记 2024/12/3 9:24:04

活着就好20241202

亲爱的朋友们&#xff0c;大家早上好&#xff01;今天是2024年12月2日&#xff0c;第49周的第一天&#xff0c;也是十二月的第二天&#xff0c;农历甲辰[龙]年十月三十。在这个全新月份的开始、阳光初升的清晨&#xff0c;愿第一缕阳光悄悄探进你的房间&#xff0c;带给你满满的…...

编程日记 2024/12/3 9:23:02

自由学习记录（28）

C# 中的流&#xff08;Stream&#xff09; 流&#xff08;Stream&#xff09;是用于读取和写入数据的抽象基类。 流表示从数据源读取或向数据源写入数据的矢量过程。 C# 中的流类是从 System.IO.Stream 基类派生的&#xff0c;提供了多种具体实现&#xff0c;每种实现都针对…...

编程日记 2024/12/3 9:15:54

操作系统、虚拟化技术与云原生01

操作系统基础 操作系统定义 OS声明了软件怎么调用硬件&#xff0c;同时支持人机交互 人机交互的过程&#xff1a; shell是人机交互转换的虚拟环境&#xff0c;内核只能识别0、1组成的数据流&#xff0c;底层资源只能识别电流的变化 操作系统的组成 1. 进程管理 进程定义&#x…...

编程日记 2024/12/3 9:13:49

linux的挂卸载

挂卸载操作 在 Linux 系统中&#xff0c;挂载&#xff08;mount&#xff09;和卸载&#xff08;umount&#xff09;是管理文件系统和存储设备的核心操作。通过这两个操作&#xff0c;我们可以将设备&#xff08;如硬盘、光盘、U盘等&#xff09;或网络文件系统的内容集成到系统…...

编程日记 2024/12/3 9:11:47

【和春笋一起学C++】OpenCV中数组和指针运用实例

前言&#xff1a;前面学习了数组和指针在C中的处理原理&#xff0c;本文通过自己编写一个图像处理的函数实例来加深对数组和指针的理解。为什么是图像处理呢&#xff0c;因为图像数据是一个二维矩阵&#xff0c;相当于一个二维数组&#xff0c;前面学习了一维数组&#xff0c;现…...

编程日记 2024/12/3 9:08:44

练习（含atoi的模拟实现,自定义类型等练习）

一、结构体大小的计算及位段 &#xff08;结构体大小计算及位段 详解请看&#xff1a;自定义类型&#xff1a;结构体进阶-CSDN博客&#xff09; 1.在32位系统环境&#xff0c;编译选项为4字节对齐&#xff0c;那么sizeof(A)和sizeof(B)是多少&#xff1f; #pragma pack(4)st…...

编程新知 2026/1/30 15:16:30

多场景 OkHttpClient 管理器 - Android 网络通信解决方案

下面是一个完整的 Android 实现&#xff0c;展示如何创建和管理多个 OkHttpClient 实例&#xff0c;分别用于长连接、普通 HTTP 请求和文件下载场景。 <?xml version"1.0" encoding"utf-8"?> <LinearLayout xmlns:android"http://schemas…...

编程新知 2025/12/15 1:34:37

Cesium1.95中高性能加载1500个点

一、基本方式&#xff1a; 图标使用.png比.svg性能要好 <template><div id"cesiumContainer"></div><div class"toolbar"><button id"resetButton">重新生成点</button><span id"countDisplay&qu…...

编程新知 2025/12/17 2:10:10

2024年赣州旅游投资集团社会招聘笔试真

2024年赣州旅游投资集团社会招聘笔试真 题 ( 满 分 1 0 0 分 时 间 1 2 0 分 钟 ) 一、单选题(每题只有一个正确答案，答错、不答或多答均不得分) 1.纪要的特点不包括()。 A.概括重点 B.指导传达 C. 客观纪实 D.有言必录 【答案】: D 2.1864年，()预言了电磁波的存在，并指出…...

编程新知 2025/12/10 4:08:53

论文解读：交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架（一）

宇树机器人多姿态起立控制强化学习框架论文解析 论文解读&#xff1a;交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架&#xff08;一&#xff09; 论文解读&#xff1a;交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化…...

编程新知 2025/8/27 0:58:09

GitHub 趋势日报 (2025年06月08日)

&#x1f4ca; 由 TrendForge 系统生成 | &#x1f310; https://trendforge.devlive.org/ &#x1f310; 本日报中的项目描述已自动翻译为中文 &#x1f4c8; 今日获星趋势图 今日获星趋势图 884 cognee 566 dify 414 HumanSystemOptimization 414 omni-tools 321 note-gen …...

编程新知 2025/12/13 1:32:15

Hive 存储格式深度解析：从 TextFile 到 ORC，如何选对数据存储方案？

在大数据处理领域&#xff0c;Hive 作为 Hadoop 生态中重要的数据仓库工具&#xff0c;其存储格式的选择直接影响数据存储成本、查询效率和计算资源消耗。面对 TextFile、SequenceFile、Parquet、RCFile、ORC 等多种存储格式&#xff0c;很多开发者常常陷入选择困境。本文将从底…...

编程新知 2025/12/6 10:54:35

django blank 与 null的区别

1.blank blank控制表单验证时是否允许字段为空 2.null null控制数据库层面是否为空 但是&#xff0c;要注意以下几点&#xff1a; Django的表单验证与null无关&#xff1a;null参数控制的是数据库层面字段是否可以为NULL&#xff0c;而blank参数控制的是Django表单验证时字…...

编程新知 2025/7/7 3:34:13

数据库正常，但后端收不到数据原因及解决

从代码和日志来看&#xff0c;后端SQL查询确实返回了数据&#xff0c;但最终user对象却为null。这表明查询结果没有正确映射到User对象上。 在前后端分离&#xff0c;并且ai辅助开发的时候&#xff0c;很容易出现前后端变量名不一致情况&#xff0c;还不报错&#xff0c;只是单…...

编程新知 2026/1/1 2:56:38

数据结构：泰勒展开式：霍纳法则（Horner‘s Rule）

目录 &#x1f50d; 若用递归计算每一项&#xff0c;会发生什么&#xff1f; Horners Rule&#xff08;霍纳法则&#xff09; 第一步&#xff1a;我们从最原始的泰勒公式出发 第二步&#xff1a;从形式上重新观察展开式 &#x1f31f; 第三步&#xff1a;引出霍纳法则&…...

编程新知 2026/2/4 23:58:11