2021数学分析【南昌大学】
2021 数学分析
-
求极限
lim n → ∞ 1 n ( n + 1 ) ( n + 2 ) ⋯ ( n + n ) n \lim_{n \to \infty} \frac{1}{n} \sqrt [n]{(n+1)(n+2) \cdots (n+n)} n→∞limn1n(n+1)(n+2)⋯(n+n)
lim n → ∞ 1 n ( n + 1 ) ( n + 2 ) ⋯ ( n + n ) n = lim n → ∞ ( n + 1 ) ( n + 2 ) ⋯ ( n + n ) n m n = lim n → ∞ e 1 n ∑ k = 1 n ln ( 1 + k n ) = e ∫ 0 1 ln ( 1 + x ) d x = e 2 l n 2 − 1 \begin{align*} \mathop {\lim }\limits_{n \to \infty } \frac{1}{n} \sqrt [n]{{(n + 1)(n + 2) \cdots (n + n)}} &= \mathop {\lim }\limits_{n \to \infty } \sqrt [n]{{\frac{{(n + 1)(n + 2) \cdots (n + n)}}{{n^m}}}} \\ &= \mathop {\lim }\limits_{n \to \infty } e^{\frac{1}{n} \sum\limits_{k = 1}^n \ln\left( 1 + \frac{k}{n} \right)} \\ &= e^{\int_0^1 \ln\left( 1 + x \right) dx} \\ &= e^{2ln2-1} \\ \end{align*} n→∞limn1n(n+1)(n+2)⋯(n+n)=n→∞limnnm(n+1)(n+2)⋯(n+n)=n→∞limen1k=1∑nln(1+nk)=e∫01ln(1+x)dx=e2ln2−1
-
求 a , b a, b a,b 的值,使得
lim x → 0 1 b x − sin x ∫ 0 x t 2 a + t 2 d t = 1. \lim_{x \to 0} \frac{1}{bx - \sin x} \int_0^x \frac{t^2}{\sqrt{a + t^2}} \, dt = 1. x→0limbx−sinx1∫0xa+t2t2dt=1.
lim x → 0 ∫ 0 x t 2 a + t 2 d t b x − sin x = lim x → 0 x 2 ( b − cos x ) a + x 2 = lim x → 0 x 2 ( b − 1 + 1 2 x 2 + o ( x 2 ) ) ( a + 1 2 a x 2 + o ( x 2 ) ) = lim x → 0 x 2 ( ( b − 1 ) a + 1 2 ( a + b − 1 a ) x 2 + o ( x 2 ) ) = 1 \begin{aligned} \mathop{\lim}\limits_{x \to 0} \frac{\int_0^x \frac{t^2}{\sqrt{a + t^2}} \, dt}{bx - \sin x} &= \mathop{\lim}\limits_{x \to 0} \frac{x^2}{\left( b - \cos x \right) \sqrt{a + x^2}} \\ &= \mathop{\lim}\limits_{x \to 0} \frac{x^2}{\left( b - 1 + \frac{1}{2}x^2 + o(x^2) \right)\left( \sqrt{a} + \frac{1}{2\sqrt{a}}x^2 + o(x^2) \right)} \\ &= \mathop{\lim}\limits_{x \to 0} \frac{x^2}{\left( \left( b - 1 \right)\sqrt{a} + \frac{1}{2}\left( \sqrt{a} + \frac{b - 1}{\sqrt{a}} \right)x^2 + o(x^2) \right)} \\ &= 1 \end{aligned} x→0limbx−sinx∫0xa+t2t2dt=x→0lim(b−cosx)a+x2x2=x→0lim(b−1+21x2+o(x2))(a+2a1x2+o(x2))x2=x→0lim((b−1)a+21(a+ab−1)x2+o(x2))x2=1
当 a ≠ 0 a\ne0 a=0
解得 ( b − 1 ) a = 0 (b-1)\sqrt{a}=0 (b−1)a=0 ,且 1 2 ( a + b − 1 a ) = 1 \frac{1}{2}\left( \sqrt{a} + \frac{b - 1}{\sqrt{a}} \right)=1 21(a+ab−1)=1
故 b = 1 b=1 b=1, a = 4 a=4 a=4
当 a = 0 a=0 a=0,极限不成立

- 用定义法证明 y = x 2 y = x^2 y=x2 在 ( − 1 , 2 ) (-1, 2) (−1,2) 上一致连续,在 ( 0 , + ∞ ) (0, +\infty) (0,+∞) 上不一致连续。
任取 x 1 , x 2 ∈ ( − 1 , 2 ) x_1,x_2 \in(-1,2) x1,x2∈(−1,2),要使不等式
∣ x 2 2 − x 1 2 ∣ = ∣ x 2 − x 1 ∣ ∣ x 2 + x 1 ∣ ≤ 4 ∣ x 2 − x 1 ∣ < ε \left| x_2^2 - x_1^2 \right| = \left| x_2 - x_1 \right| \left| x_2 + x_1 \right| \leq 4\left| x_2 - x_1 \right| < \varepsilon x22−x12 =∣x2−x1∣∣x2+x1∣≤4∣x2−x1∣<ε
成立,解得 ∣ x 2 − x 1 ∣ < ε 4 \left| x_2 - x_1 \right| < \frac{\varepsilon}{4} ∣x2−x1∣<4ε,取 δ 1 = ε 4 \delta_1= \frac{\varepsilon}{4} δ1=4ε
则 ∀ x 1 , x 2 ∈ ( − 1 , 2 ) \forall x_1,x_2 \in(-1,2) ∀x1,x2∈(−1,2),当 ∣ x 2 − x 1 ∣ < δ 1 \left| x_2 - x_1 \right| <\delta_1 ∣x2−x1∣<δ1,有 ∣ x 2 2 − x 1 2 ∣ < ε \left| x_2^2 - x_1^2 \right| < \varepsilon x22−x12 <ε,故在 ( − 1 , 2 ) (-1, 2) (−1,2) 上一致连续
取 x n = n x_n=\sqrt n xn=n, y n = n + 1 y_n=\sqrt {n+1} yn=n+1
lim n → ∞ ( y n − x n ) = lim n → ∞ ( n + 1 − n ) = lim n → ∞ 1 n + 1 + n = 0 \begin{aligned} \mathop{\lim}\limits_{n \to \infty} (y_n - x_n) &= \mathop{\lim}\limits_{n \to \infty} \left( \sqrt{n+1} - \sqrt{n} \right) \\ &= \mathop{\lim}\limits_{n \to \infty} \frac{1}{\sqrt{n+1} + \sqrt{n}} \\ &= 0 \end{aligned} n→∞lim(y
相关文章:

2021数学分析【南昌大学】
2021 数学分析 求极限 lim n → ∞ 1 n ( n + 1 ) ( n + 2 ) ⋯ ( n + n ) n \lim_{n \to \infty} \frac{1}{n} \sqrt [n]{(n+1)(n+2) \cdots (n+n)} n→∞limn1n(n+1)(n+2)⋯(n+n) lim n → ∞ 1 n ( n + 1 ) ( n + 2 ) ⋯ ( n + n ) n = lim n → ∞ ( n + …...

单端和差分信号的接线法
内容来源:【单端信号 差分信号与数据采集卡的【RSE】【 NRES】【 DIFF】 模式的连接】 此篇文章仅作笔记分享。 单端输入 单端信号指的是输入信号由一个参考端和一个信号端构成,参考端一般是地端,信号就是通过计算信号端口和地端的差值所得…...

力扣-图论-2【算法学习day.52】
前言 ###我做这类文章一个重要的目的还是给正在学习的大家提供方向和记录学习过程(例如想要掌握基础用法,该刷哪些题?)我的解析也不会做的非常详细,只会提供思路和一些关键点,力扣上的大佬们的题解质量是非…...

MySQL如何区分幻读和不可重复读
在MySQL中,幻读和不可重复读都是并发事务中可能出现的问题,但它们的表现和原因略有不同。 不可重复读 (Non-Repeatable Read) 不可重复读是指在同一个事务内,多次读取同一行数据时,可能会得到不同的结果。这种情况发生在一个事务…...

界面控件Syncfusion Essential Studio®现在已完全支持 .NET 9
Syncfusion Essential Studio现在完全支持 .NET 9,可最新版本2024 Volume 3 版本中使用!通过此更新,Blazor、.NET MAUI、WPF、WinForms、WinUI和ASP.NET Core 平台中的 Syncfusion 组件以及文档处理库已准备好让您利用 .NET 9 中的最新功能。…...

openEuler安装lsb_release
lsb_release是linux下查看发行版信息用的工具 lsb_release只是一个小程序,它的包名并不是lsb_release lsb_release其实是红帽的一个项目,其名为redhat-lsb 我们的lsb_release就是其中的一部分,更准确的说是redhat-lsb-core 从网站࿱…...

统计数字字符个数
统计数字字符个数 C语言实现C实现Java实现Python实现 💐The Begin💐点点关注,收藏不迷路💐 输入一行字符,统计出其中数字字符的个数。 输入 一行字符串,总长度不超过255。 输出 出为1行,输出…...

44页PDF | 信息化战略规划标准框架方法论与实施方法(限免下载)
一、前言 这份报告详细介绍了企业信息化战略规划的标准框架、方法论以及实施方法,强调了信息化规划应以业务战略和IT战略为驱动力,通过构筑企业架构(EA)来连接长期战略和信息化建设。报告提出了信息化规划原则,探讨了…...

计算机网络期末复习-part1-概述
1、互联网的组成 互联网由两大块组成。 1、边沿部分:由所有连接在互联网上的主机组成,是用户直接使用的部分。 2、核心部分,由大量网络和路由器组成,为边缘部分提供服务。 2、数据传送阶段的三种交换方式的主要特点 1、电路交…...

A1228 php+Mysql旅游供需平台的设计与实现 导游接单 旅游订单 旅游分享网站 thinkphp框架 源码 配置 文档 全套资料
旅游供需平台 1.项目描述2. 开发背景与意义3.项目功能4.界面展示5.源码获取 1.项目描述 随着社会经济的快速发展,生活水平的提高,人们对旅游的需求日益增强,因此,为给用户提供一个便利的查看导游信息,进行导游招募的平…...

RabbitMQ消息可靠性保证机制5--消息幂等性处理
RabbitMQ层面有实现“去重机制”来保证“恰好一次”吗?答案是没并没有,而且现在主流的消息中间件都没有实现。 一般解决重复消息的办法是:在消费端让我们消费消息操作具有幂等性。 幂等性问题并不是消息系统独有,而是࿰…...

Claude3.5如何使用?
Claude 3.5 Sonnet,性能直接吊打了 GPT-4o,甚至价格还更便宜。网友们纷纷展开实测,有人表示自己一半的工作已经可以由它替代了!而最让人惊喜的新功能,莫过于 Artifacts 了。 就在昨天,Anthropic 深夜发布了…...

力扣刷题TOP101:14.BM16 删除有序链表中重复的元素-II
目录: 目的 思路 复杂度 记忆秘诀 python代码 目的 1→1→2→3→3 删除重复后变成2。 思路 这个任务是删除链表里重复的节点包含本身。可以看成是一个抽奖活动的系统升级。某人通过多种方式报名(节点不同),后台数据检测到这些…...

解决github网络慢的问题
前言 本文采用替换host的方式来加速github的git请求,主要我自己用来备份的懒人方式,不然每次都要手动修改hosts文件,skrskrskr… 一、获取到可用的ip 先到这个网站查询到低延迟的ip 站长工具:https://ping.chinaz.com/ 第2步&…...

docker及docker exec命令学习笔记
docker exec 是一个常用的 Docker 命令,允许你在已经运行的容器中执行命令或启动新的进程。以下是详细介绍和常见用法: 基本语法 docker exec [OPTIONS] CONTAINER COMMAND [ARG...]参数详解 1. CONTAINER指定目标容器的名字或容器 ID。可以通过以下命…...

linux环境宝塔服务部署安装及介绍
一、简介 宝塔面板是一款服务器管理软件,支持windows和linux系统,可以通过Web端轻松管理服务器,提升运维效率。例如:创建管理网站、FTP、数据库,拥有可视化文件管理器,可视化软件管理器,可视化C…...
概念与应用: 中英双语)
充分统计量(Sufficient Statistic)概念与应用: 中英双语
充分统计量:概念与应用 在统计学中,充分统计量(Sufficient Statistic) 是一个核心概念。它是从样本中计算得出的函数,能够完整且无损地表征样本中与分布参数相关的信息。在参数估计中,充分统计量能够帮助我…...
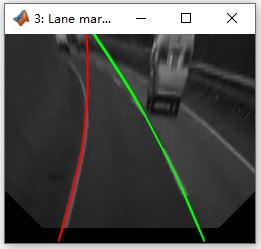
基于Matlab计算机视觉的车道线识别与前车检测系统研究
随着自动驾驶技术的发展,车道线识别和前车检测成为智能驾驶系统中的核心技术之一。本实训报告围绕基于计算机视觉的车道线识别与前车检测系统展开,旨在通过处理交通视频数据,实时检测车辆所在车道及其与前车的相对位置,从而为车道…...

模糊测试中常见的10种变异mutation策略
1. 引入 基于变异策略的模糊测试,有两个重点: (1)seed:种子,初始的合法输入序列。 (2)mutation:对已经存在的输入序列,进行微调。 所以,mutatio…...
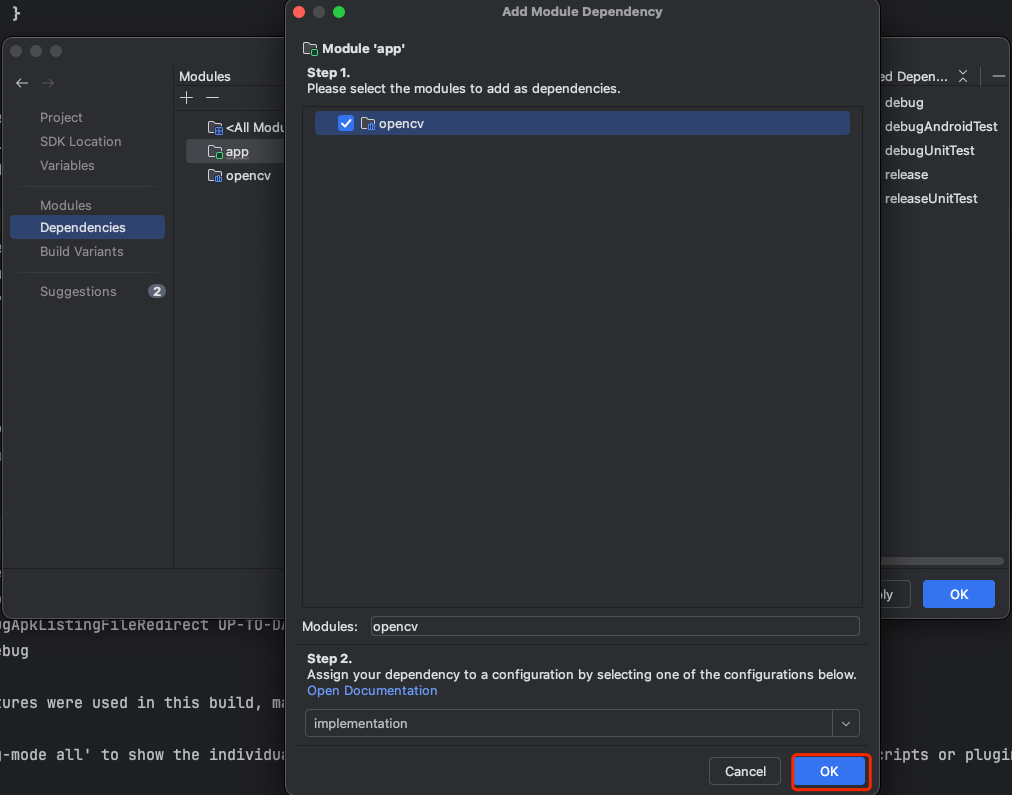
opencv-android编译遇到的相关问题处理
1、opencv-android sdk下载 下载地址:https://opencv.org/releases/ 下载安卓SDK即可 2、解压下载好的SDK 3、导入opencv的SDK到安卓项目中 导入步骤在/OpenCV-android-sdk/sdk/build.gradle文件的注释中写的非常详细,大家可安装官方给出的步骤导入。…...

日语AI面试高效通关秘籍:专业解读与青柚面试智能助攻
在如今就业市场竞争日益激烈的背景下,越来越多的求职者将目光投向了日本及中日双语岗位。但是,一场日语面试往往让许多人感到步履维艰。你是否也曾因为面试官抛出的“刁钻问题”而心生畏惧?面对生疏的日语交流环境,即便提前恶补了…...

C++实现分布式网络通信框架RPC(3)--rpc调用端
目录 一、前言 二、UserServiceRpc_Stub 三、 CallMethod方法的重写 头文件 实现 四、rpc调用端的调用 实现 五、 google::protobuf::RpcController *controller 头文件 实现 六、总结 一、前言 在前边的文章中,我们已经大致实现了rpc服务端的各项功能代…...

【android bluetooth 框架分析 04】【bt-framework 层详解 1】【BluetoothProperties介绍】
1. BluetoothProperties介绍 libsysprop/srcs/android/sysprop/BluetoothProperties.sysprop BluetoothProperties.sysprop 是 Android AOSP 中的一种 系统属性定义文件(System Property Definition File),用于声明和管理 Bluetooth 模块相…...

HarmonyOS运动开发:如何用mpchart绘制运动配速图表
##鸿蒙核心技术##运动开发##Sensor Service Kit(传感器服务)# 前言 在运动类应用中,运动数据的可视化是提升用户体验的重要环节。通过直观的图表展示运动过程中的关键数据,如配速、距离、卡路里消耗等,用户可以更清晰…...
提供了哪些便利?)
现有的 Redis 分布式锁库(如 Redisson)提供了哪些便利?
现有的 Redis 分布式锁库(如 Redisson)相比于开发者自己基于 Redis 命令(如 SETNX, EXPIRE, DEL)手动实现分布式锁,提供了巨大的便利性和健壮性。主要体现在以下几个方面: 原子性保证 (Atomicity)ÿ…...

Kubernetes 网络模型深度解析:Pod IP 与 Service 的负载均衡机制,Service到底是什么?
Pod IP 的本质与特性 Pod IP 的定位 纯端点地址:Pod IP 是分配给 Pod 网络命名空间的真实 IP 地址(如 10.244.1.2)无特殊名称:在 Kubernetes 中,它通常被称为 “Pod IP” 或 “容器 IP”生命周期:与 Pod …...

算法打卡第18天
从中序与后序遍历序列构造二叉树 (力扣106题) 给定两个整数数组 inorder 和 postorder ,其中 inorder 是二叉树的中序遍历, postorder 是同一棵树的后序遍历,请你构造并返回这颗 二叉树 。 示例 1: 输入:inorder [9,3,15,20,7…...

Vue 3 + WebSocket 实战:公司通知实时推送功能详解
📢 Vue 3 WebSocket 实战:公司通知实时推送功能详解 📌 收藏 点赞 关注,项目中要用到推送功能时就不怕找不到了! 实时通知是企业系统中常见的功能,比如:管理员发布通知后,所有用户…...

【版本控制】GitHub Desktop 入门教程与开源协作全流程解析
目录 0 引言1 GitHub Desktop 入门教程1.1 安装与基础配置1.2 核心功能使用指南仓库管理日常开发流程分支管理 2 GitHub 开源协作流程详解2.1 Fork & Pull Request 模型2.2 完整协作流程步骤步骤 1: Fork(创建个人副本)步骤 2: Clone(克隆…...
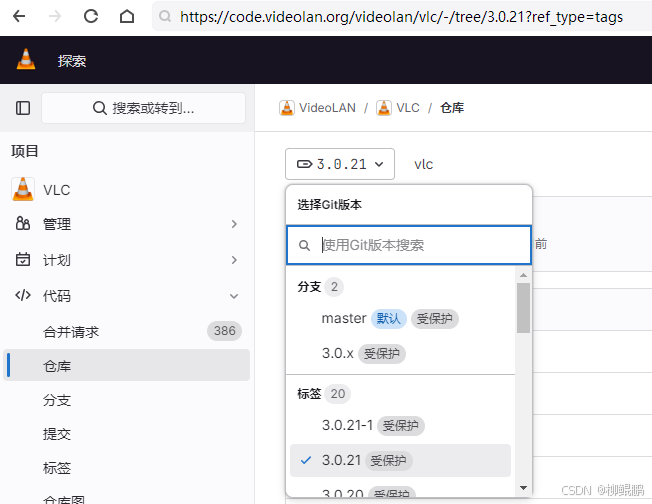
LINUX编译vlc
下载 VideoLAN / VLC GitLab 选择最新的发布版本 准备 sudo apt install -y xcb bison sudo apt install -y autopoint sudo apt install -y autoconf automake libtool编译ffmpeg LINUX FFMPEG编译汇总(最简化)_底部的附件列表中】: ffmpeg - lzip…...
