【实分析】【二】2.2 (c)自然数的序
文章目录
- 前言
- 一、自然数的序的定义
- 二、自然数的序的基本性质
- 三、序的三歧性
- 四、强归纳法原理
- 总结
前言
在2.2 (b)的末尾,我们定义了自然数的正性,现在,我们来定义自然数的序,它是一种自然数的二元关系,通过加法进行定义。
一、自然数的序的定义
自然数的序定义如下:设n和m是自然数,我们称n大于等于m,记为 n ≥ m , m ≤ n n\geq m, m\leq n n≥m,m≤n,当且仅当存在自然数a,使得 n = m + a n=m+a n=m+a;我们称n严格大于m,记为 n > m , m < n n> m,m< n n>m,m<n,当且仅当 n ≥ m , n ≠ m n\geq m, n\neq m n≥m,n=m。
这个定义理解起来还是非常直观易懂的,没有需要过多赘述的地方。由于任意一个自然数 x x x都可以找到自然数x,使得 x = 0 + x x=0+x x=0+x,所以有 0 ≤ x 0\le x 0≤x。而对任意正自然数也就有 0 < x 0<x 0<x。
二、自然数的序的基本性质
下面我们来看序的基本性质:
a. (序是自反的) a ≥ a a\geq a a≥a
b. (序是传递的) a ≥ b , b ≥ c a\geq b, b\geq c a≥b,b≥c, 则 a ≥ c a\geq c a≥c
c. (序是反对称的) a ≥ b , b ≥ a a\geq b, b\geq a a≥b,b≥a,则 a = b a=b a=b
d. (加法保序) a ≥ b a\geq b a≥b,当且仅当 a + c ≥ b + c a+c\geq b+c a+c≥b+c
e. a < b a<b a<b,当且仅当 a + + ≤ b a++\le b a++≤b
f. a < b a<b a<b,当且仅当存在某个正数 d d d 满足 b = a + d b=a+d b=a+d
这些基本性质都很符合直观理解,证明也都比较简单,我们来依次证明一下:
a. 证明: ∃ \exist ∃ 自然数0,使得 a + 0 = a a+0=a a+0=a, ∴ a ≥ a \therefore a\geq a ∴a≥a
b. 证明: ∵ a ≥ b , b ≥ c \because a\ge b, b\ge c ∵a≥b,b≥c,
∴ ∃ \therefore \exist ∴∃ 自然数 x , y x, y x,y 满足 a = b + x , b = c + y a=b+x, b=c+y a=b+x,b=c+y
∴ a = c + y + x \therefore a=c+y+x ∴a=c+y+x
∴ a ≥ c \therefore a\geq c ∴a≥c
c. 证明:$\exist $ 自然数 x , y x,y x,y 满足 a = b + x , b = a + y a=b+x, b=a+y a=b+x,b=a+y
∴ a = a + y + x \therefore a=a+y+x ∴a=a+y+x,由消去律有: 0 = x + y 0=x+y 0=x+y
∴ x = y = 0 , a = b \therefore x=y=0, a=b ∴x=y=0,a=b
d. 证明:i). “=>” ∵ a ≥ b \because a\geq b ∵a≥b
∴ a = b + x , a + c = b + c + x \therefore a=b+x, a+c=b+c+x ∴a=b+x,a+c=b+c+x
∴ a + c ≥ b + c \therefore a+c\geq b+c ∴a+c≥b+c
ii). “<=” ∵ a + c ≥ b + c \because a+c\geq b+c ∵a+c≥b+c
∴ a + c = b + c + x \therefore a+c=b+c+x ∴a+c=b+c+x,由消去律有: a = b + x a=b+x a=b+x
∴ a ≥ b \therefore a\geq b ∴a≥b
e. 证明:i). “=>” ∵ a < b \because a< b ∵a<b,
∴ b = a + x \therefore b=a+x ∴b=a+x
假设 x = 0 x=0 x=0,则有 a = b a=b a=b,矛盾!因此 x x x为正。
∴ ∃ \therefore \exist ∴∃ 自然数 y y y 满足 x = y + + x=y++ x=y++
∴ b = a + y + + = ( a + + ) + y \therefore b=a+y++=(a++)+y ∴b=a+y++=(a++)+y
∴ a + + ≤ b \therefore a++\le b ∴a++≤b
ii). “<=” ∵ a + + ≤ b \because a++\le b ∵a++≤b
∴ b = ( a + + ) + x = a + x + + \therefore b=(a++)+x=a+x++ ∴b=(a++)+x=a+x++
∴ a ≤ b \therefore a\le b ∴a≤b
假设 a = b a=b a=b,则 a = a + x + + a=a+x++ a=a+x++,由消去律有 0 = x + + 0=x++ 0=x++
由Peano公理可知,0不是任何自然数的后继,矛盾!因此 a ≠ b a\neq b a=b
∴ a < b \therefore a<b ∴a<b
f. 证明:i). “=>” ∵ a < b \because a<b ∵a<b
∴ b = a + d \therefore b=a+d ∴b=a+d. 由e中可知 d d d为正。
ii). “<=” ∵ b = a + d \because b=a+d ∵b=a+d
∴ a ≤ b \therefore a\le b ∴a≤b
假设 a = b ,则有 a = a + d , 0 = d 假设a=b,则有a=a+d,0=d 假设a=b,则有a=a+d,0=d,矛盾!因此, a ≠ b a\neq b a=b
∴ a < b \therefore a<b ∴a<b
这些性质的证明都不难,把之前已经掌握的推论命题都利用一下就能轻松得证。
三、序的三歧性
所谓序的三歧性是指对于任意两个自然数 a , b a,b a,b,下列三个命题恰有一个为真: a < b , a = b , a > b a<b,a=b,a>b a<b,a=b,a>b。
这个性质也就决定了自然数之间的序的关系只能是这三种情况中的一种。这个性质证明也不难,**证明思路如下:**由序的定义,容易知道第一个和第三个命题均与第二个命题是互斥的,则他们无法同时为真。然后再说明第一第三也无法同时为真,则说明了只能有一个命题为真。后面再证至少一个命题为真即可。
证明:i) ∵ a < b = > a ≠ b , a > b = > a ≠ b \because a<b =>a\neq b, a>b => a\neq b ∵a<b=>a=b,a>b=>a=b
∴ a = b \therefore a=b ∴a=b 与 a < b a<b a<b 或者 a > b a>b a>b 不同时为真。
假设 a < b , a > b a<b, a>b a<b,a>b同时为真
∵ a < b = > a ≤ b , a > b = > a ≥ b \because a<b => a\leq b, a>b => a\ge b ∵a<b=>a≤b,a>b=>a≥b
∴ a = b \therefore a=b ∴a=b 矛盾!因此任意两个命题不同时为真。
ii) 固定b,对a使用归纳法证明三个命题中至少一个为真:
验证 P ( 0 ) P(0) P(0) 为真:若b为0,则 a = b = 0 a=b=0 a=b=0为真。若b为正数,则 b > a = 0 b>a=0 b>a=0为真。
设 P ( a ) P(a) P(a) 为真,则有三个命题中至少一个为真。
下证 P ( a + + ) P(a++) P(a++)为真:
- 若 a = b a=b a=b 为真,则有 a + + = b + + = b + 1 a++=b++=b+1 a++=b++=b+1, ∵ 1 \because 1 ∵1 为正
∴ a + + > b \therefore a++>b ∴a++>b 为真- 若 a > b a>b a>b 为真,则 ∃ \exist ∃ 正数 x x x 满足 a = b + x a=b+x a=b+x
∴ a + + = ( b + x ) + + = b + x + + \therefore a++ = (b+x)++=b+x++ ∴a++=(b+x)++=b+x++,
由Peano公理可知 ∵ x + + \because x++ ∵x++ 为正,则 a + + > b a++>b a++>b 为真- 若 a < b a<b a<b 为真,由序的基本性质 e 可知 a + + ≤ b a++\le b a++≤b
∴ ∃ \therefore \exist ∴∃ 自然数 x x x 满足 b = x + a + + b=x+a++ b=x+a++
若 x 为0,则有 b = a + + b=a++ b=a++为真;若 x 为正,由序的基本性质 f 有 b > a + + b>a++ b>a++为真。
由消去律易知这样的 x 是唯一的,而自然数 x 只能为0或者不是0(即为正)。
∴ b > a + + , b = a + + \therefore b>a++, b=a++ ∴b>a++,b=a++ 至少有一个为真。
因此, a + + > b , a + + = b , a + + < b a++>b,a++=b,a++<b a++>b,a++=b,a++<b至少有一个为真 。
从而,如上三个命题有且只有一个为真。
有了这个三歧性,以后对于自然数之间的序关系就可以使用排除法来分析,即若已知其中两个命题为假,第三个命题必为真。同样若一个命题为真,则另外两个必为假。
四、强归纳法原理
由序的性质,可以得到归纳法原理的更强形式——强归纳原理:
设 m 0 m_0 m0 是一个自然数,而 P ( m ) P(m) P(m) 是依赖于自然数 m 的一个性质。 设对于每个 m ≤ m 0 m\le m_0 m≤m0 都有 若 ∀ m 0 ≤ m ′ < m , P ( m ′ ) \forall m_0\le m'< m, P(m') ∀m0≤m′<m,P(m′) 为真,则 P ( m ) P(m) P(m) 也为真 的关系,(特别的,当 m = m 0 m=m_0 m=m0 时,条件为空,因此 P ( m 0 ) P(m_0) P(m0) 为真)则可以断定 P ( m ) P(m) P(m) 对 ∀ m ≥ m 0 \forall m\ge m_0 ∀m≥m0成立。
对比强归纳原理与2.1 Peano公理中的弱归纳原理,可以看到在起始条件上,不再是从0开始归纳,而是可以从任意使得性质 P ( m 0 ) P(m_0) P(m0) 为真的自然数 m 0 m_0 m0 开始。其次,在归纳性上,也放宽了要求:
弱归纳法的归纳性要求:必须仅仅依靠 P ( n ) P(n) P(n) 为真,就推出 P ( n + + ) P(n++) P(n++) 为真。
强归纳法的归纳性要求:可以借助 P ( m ′ ) P(m') P(m′) 为真,推出 P ( m ) P(m) P(m) 为真。
这两个归纳法的强弱的理解可能稍微有点绕,我们简单梳理一下:弱归纳法的归纳性要求中给定的条件更少(只有 P ( n ) P(n) P(n) 为真),需要能够推出的结论确实相同(即P对下一个自然数为真),所以该归纳法对性质P具有更严苛的要求,所以该归纳法能适用的情况更少,也就是更弱。
其实,当性质P满足若归纳法的归纳性要求时,则必然满足强归纳法的归纳性要求。如果只需要 P ( n ) P(n) P(n) 为真就能推出 P ( n + + ) P(n++) P(n++) 为真,则加上前面的多余条件也一样可以推出 P ( n + + ) P(n++) P(n++) 为真。
啰嗦了这么久,理清了强弱归纳法的关系,下面我们来证明一下强归纳原理。首先整理一下证需要证明的内容:若一个性质对自然数满足强归纳性要求,且存在某个起始自然数 m 0 m_0 m0 为真,那么借由这种强归纳性需要能够推出该性质对任意大于起始自然数的自然数为真。
要证明强归纳原理,势必要往弱归纳原理上靠,所以需要把强归纳性中要求的对一群自然数成立的条件变成对单个自然数成立,且这个单个自然数还必须是我们的归纳对象,从而可以使用弱归纳法进行归纳推理。因此将 P ( m ′ ) P(m') P(m′) 对一切 m 0 ≤ m ′ < m m_0\le m'<m m0≤m′<m 打包成一个性质 Q ( m ) Q(m) Q(m)。只要证明 Q ( m ) Q(m) Q(m) 对任意自然数为真即可。
证明:定义性质 Q ( m ) Q(m) Q(m) 表示: P ( m ) P(m) P(m) 对一切 m 0 ≤ m ′ < m m_0\le m'<m m0≤m′<m 成立。当 m < m 0 m<m_0 m<m0时, m ′ m' m′ 为空集, P ( m ′ ) P(m') P(m′) 为真, Q ( m ) Q(m) Q(m) 也为真。(可以这么考虑,空集中找不出任意元素使得P为假。)
对 m m m 进行归纳。
∴ Q ( 0 ) 为真 \therefore Q(0) 为真 ∴Q(0)为真
设 Q ( m ) Q(m) Q(m) 为真,则有 P ( m ′ ) P(m') P(m′) 对一切 m 0 ≤ m ′ < m m_0\le m'<m m0≤m′<m 为真
下证 Q ( m + + ) Q(m++) Q(m++) 为真:
由强归纳法的归纳性可知,若 P ( m ′ ) P(m') P(m′) 对一切 m 0 ≤ m ′ < m m_0\le m'<m m0≤m′<m 为真,则有 P ( m ) P(m) P(m) 为真。
∴ P ( m ′ ) \therefore P(m') ∴P(m′) 对一切 m 0 ≤ m ′ < m + + m_0\le m'< m++ m0≤m′<m++ 为真。即 Q ( m + + ) Q(m++) Q(m++) 为真。
由Peano公理中的归纳法原理可知, Q ( m ) Q(m) Q(m) 对一切自然数都为真。
即 P ( m ′ ) P(m') P(m′) 对一切 m 0 ≤ m ′ < m m_0\le m'<m m0≤m′<m 对 ∀ m \forall m ∀m 都为真。
∵ ∀ m ′ \because \forall m' ∵∀m′,我们总能找到自然数 m,使得 m ′ < m m'<m m′<m成立
∴ \therefore ∴ 上述命题对 ∀ m ′ ≥ m 0 \forall m'\ge m_0 ∀m′≥m0 均为真。
不知道是否有人会有这样的疑惑:强归纳法只要能够通过对一堆自然数成立,推导下一个自然数成立,然后再重复,不就可以推导对所有自然数成立了吗,为什么还需要证明?
个人思考:这种多米诺骨牌式的归纳推理确实是直观上容易接受的,但是弱归纳原理是一个公理,它给出了归纳法的基本框架,让我们只需要证明性质具有弱归纳性就可以推导出对全部自然数成立。因为公理中规定了自然数需要具有这种被递推归纳的性质。而强归纳原理的归纳性要求并不等同于归纳原理中的内容,也就无法直接借助公理得出对全部自然数成立的结论(这里的讨论我们暂时忽略起始自然数的问题)。一点浅薄的理解,望批评指正。
总结
本文把加法的最后一点小尾巴,自然数的序收尾了,并且介绍了强归纳法原理。
相关文章:
自然数的序)
【实分析】【二】2.2 (c)自然数的序
文章目录 前言一、自然数的序的定义二、自然数的序的基本性质三、序的三歧性四、强归纳法原理总结 前言 在2.2 (b)的末尾,我们定义了自然数的正性,现在,我们来定义自然数的序,它是一种自然数的二元关系,通过加法进行定…...
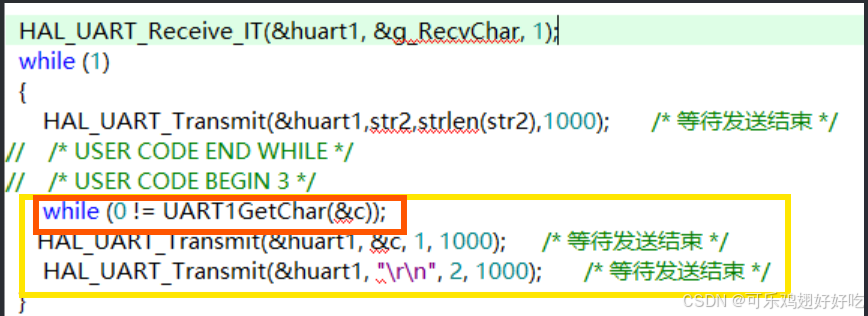
STM32串口接收与发送(关于为什么接收不需要中断而发生需要以及HAL_UART_Transmit和HAL_UART_Transmit_IT的区别)
一、HAL_UART_Transmit和HAL_UART_Transmit_IT的区别 1. HAL_UART_Transmit_IT(非阻塞模式): HAL_UART_Transmit_IT 是非阻塞的传输函数,也就是说,当你调用 HAL_UART_Transmit_IT 时,它不会等到数据完全发…...

k8s 之storageclass使用nfs动态申请PV
文章目录 配置角色权限部署nfs-client-provisioner创建 NFS StorageClass创建 PVC 来动态申请 PV在 Pod 中使用 PVC验证存储是否正确挂载使用 kubectl 和 jq 筛选 PVCwaiting for a volume to be created, either by external provisioner "nfs-diy" or manually cre…...
功能)
vue移动端实现下载(截图)功能
前言 通过html2canvas实现截图功能然后保存 简介 html2canvas库允许我们直接在浏览器上拍摄网页或部分网页的“截图”,即浏览器实现截图的功能。 原理 屏幕截图是基于DO的。其基本原理就是读取已经渲染好的DOM元素的结构和样式信息,然后基于这些信息…...

【Golang】Golang基础语法之面向对象:结构体和方法
面向对象——结构 Go 仅支持封装,不支持继承和多态;继承和多态要做的事情交给接口来完成,即——面向接口编程。Go 只有 struct,没有 class。 定义一个最简单的树节点(treeNode)结构,方法如下&…...
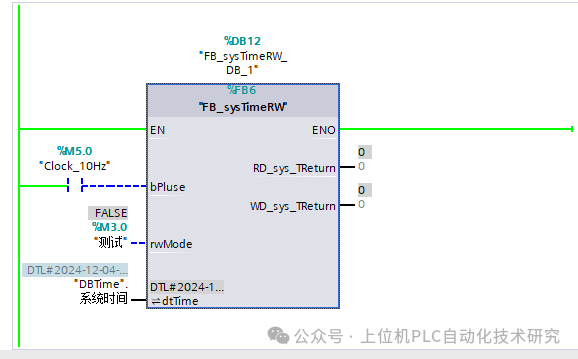
【西门子PLC.博途】——在S71200里写时间设置和读取功能块
之前我们在这篇文章中介绍过如何读取PLC的系统时间。我们来看看在西门子1200里面有什么区别。同时也欢迎关注gzh。 我们在S71200的帮助文档中搜索时间后找到这个数据类型 在博途中他是一个结构体,具体为 然后我们再看看它带的读取和写入时间块 读取时间࿱…...

位运算(一)位运算简单总结
191. 位1的个数 给定一个正整数 n,编写一个函数,获取一个正整数的二进制形式并返回其二进制表达式中 设置位 的个数(也被称为 汉明重量)。 示例 1: 输入:n 11 输出:3 解释:输入的二…...

工厂方法模式的理解和实践
在软件开发中,设计模式是一种经过验证的解决特定问题的通用方案。工厂方法模式(Factory Method Pattern)是创建型设计模式之一,它提供了一种创建对象的接口,但由子类决定要实例化的类是哪一个。工厂方法让类的实例化推…...
)
C# 设计模式--观察者模式 (Observer Pattern)
定义 观察者模式是一种行为设计模式,它定义了对象之间的一对多依赖关系,当一个对象的状态发生改变时,所有依赖于它的对象都会得到通知并自动更新。观察者模式的核心在于解耦主题(被观察者)和观察者之间的依赖关系。 …...
介绍)
【开发语言】层次状态机(HSM)介绍
层次状态机(Hierarchical State Machine, HSM),从基本原理、结构设计、实现方法以及如何结合 Qt 进行具体实现等方面进行分析。 1. 层次状态机的基本原理 层次状态机是一种用于管理复杂系统行为的状态机模型,它通过将状态组织成…...

03-13、SpringCloud Alibaba第十三章,升级篇,服务降级、熔断和限流Sentinel
SpringCloud Alibaba第十三章,升级篇,服务降级、熔断和限流Sentinel 一、Sentinel概述 1、Sentinel是什么 随着微服务的流行,服务和服务之间的稳定性变得越来越重要。Sentinel 以流量为切入点,从流量控制、熔断降级、系统负载保…...

【k8s 深入学习之 event 聚合】event count累记聚合(采用 Patch),Message 聚合形成聚合 event(采用Create)
参考 15.深入k8s:Event事件处理及其源码分析 - luozhiyun - 博客园event 模块总览 EventRecorder:是事件生成者,k8s组件通过调用它的方法来生成事件;EventBroadcaster:事件广播器,负责消费EventRecorder产生的事件,然后分发给broadcasterWatcher;broadcasterWatcher:用…...

leetcode104.二叉树的最大深度
给定一个二叉树 root ,返回其最大深度。 二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数。 示例 1: 输入:root [3,9,20,null,null,15,7] 输出:3示例 2: 输入:root [1,null,2] 输出…...
)
蓝桥杯2117砍竹子(简单易懂 包看包会版)
问题描述 这天, 小明在砍竹子, 他面前有 n 棵竹子排成一排, 一开始第 i 棵竹子的 高度为 hi. 他觉得一棵一棵砍太慢了, 决定使用魔法来砍竹子。魔法可以对连续的一 段相同高度的竹子使用, 假设这一段竹子的高度为 H, 那么 用一次魔法可以 把这一段竹子的高度都变为 ⌊H2⌋…...

LCD与lvgl
LCD与lvgl 目录 LCD与lvgl 回顾 LCD 的驱动层讲解 1、LCD 的常见接口 2、我们的 LCD 的参数 3、LCD 的设备树说明 4、LCD 的设备树说明 5、如何移植 LCD 的驱动(重点) LCD 的应用层开发 1:LCD 应用开发->界面开发的方法 2:LVGL 模拟器安装 3:LVGL 工程创建和…...

SpringBoot 赋能:精铸超稳会员制医疗预约系统,夯实就医数据根基
1绪论 1.1开发背景 传统的管理方式都在使用手工记录的方式进行记录,这种方式耗时,而且对于信息量比较大的情况想要快速查找某一信息非常慢,对于会员制医疗预约服务信息的统计获取比较繁琐,随着网络技术的发展,采用电脑…...
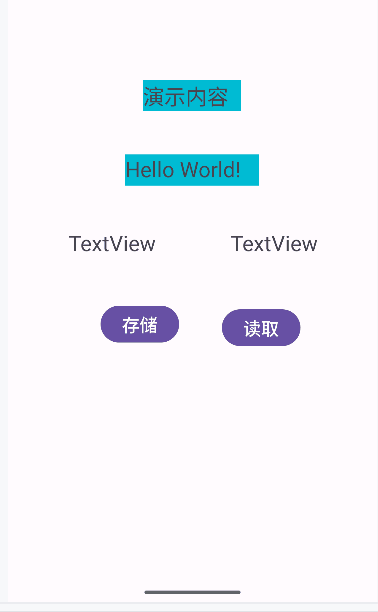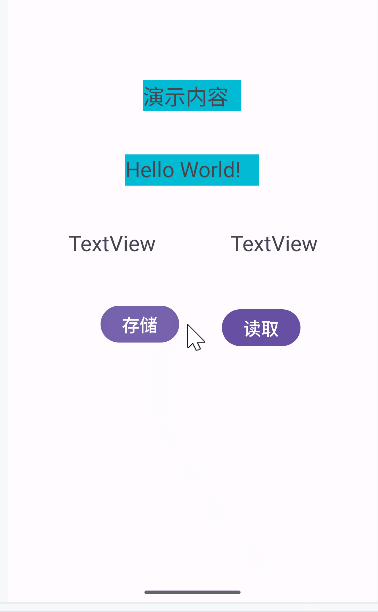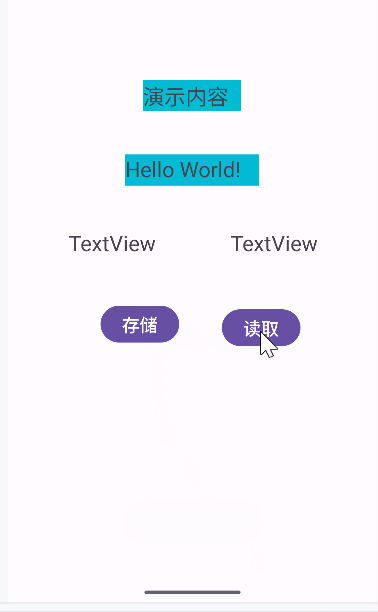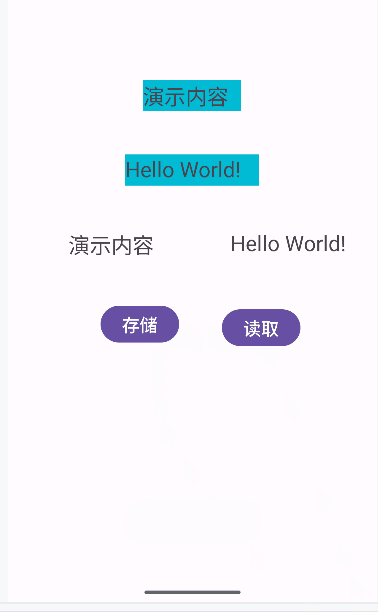
android studio 读写文件操作(应用场景二)
android studio版本:2023.3.1 patch2 例程:readtextviewIDsaveandread 本例程是个过渡例程,如果单是实现下图的目的有更简单的方法,但这个方法是下一步工作的基础,所以一定要做。 例程功能:将两个textvi…...

小尺寸低功耗蓝牙模块在光伏清扫机器人上的应用
一、引言 随着可再生能源的迅速发展,光伏发电系统的清洁与维护变得越来越重要。光伏清扫机器人通过自动化技术提高了清洁效率,而蓝牙模组的集成为这些设备提供了更为智能的管理和控制方案。 二、蓝牙模组的功能与实现: 蓝牙模组ANS-BT103M…...

防火墙有什么作用
防火墙的作用:1. 提供网络安全防护;2. 实施访问控制和流量过滤;3. 检测和阻止恶意攻击;4. 保护内部网络免受未经授权的访问;5. 监控网络流量和安全事件;6. 支持虚拟专用网络(VPN)。防…...

MongoDB-BSON 协议与类型
前言: MongoDB 是一个高性能、无模式的 NoSQL 数据库,广泛应用于大数据处理和实时数据存储。作为一个数据库系统,MongoDB 的核心之一就是其使用的 BSON(Binary JSON)格式,它用于存储数据以及在客户端和数据…...

调用支付宝接口响应40004 SYSTEM_ERROR问题排查
在对接支付宝API的时候,遇到了一些问题,记录一下排查过程。 Body:{"datadigital_fincloud_generalsaas_face_certify_initialize_response":{"msg":"Business Failed","code":"40004","sub_msg…...
)
React Native 导航系统实战(React Navigation)
导航系统实战(React Navigation) React Navigation 是 React Native 应用中最常用的导航库之一,它提供了多种导航模式,如堆栈导航(Stack Navigator)、标签导航(Tab Navigator)和抽屉…...

Java如何权衡是使用无序的数组还是有序的数组
在 Java 中,选择有序数组还是无序数组取决于具体场景的性能需求与操作特点。以下是关键权衡因素及决策指南: ⚖️ 核心权衡维度 维度有序数组无序数组查询性能二分查找 O(log n) ✅线性扫描 O(n) ❌插入/删除需移位维护顺序 O(n) ❌直接操作尾部 O(1) ✅内存开销与无序数组相…...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...

Keil 中设置 STM32 Flash 和 RAM 地址详解
文章目录 Keil 中设置 STM32 Flash 和 RAM 地址详解一、Flash 和 RAM 配置界面(Target 选项卡)1. IROM1(用于配置 Flash)2. IRAM1(用于配置 RAM)二、链接器设置界面(Linker 选项卡)1. 勾选“Use Memory Layout from Target Dialog”2. 查看链接器参数(如果没有勾选上面…...

Java-41 深入浅出 Spring - 声明式事务的支持 事务配置 XML模式 XML+注解模式
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

[Java恶补day16] 238.除自身以外数组的乘积
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O(n) 时间复杂度…...

Map相关知识
数据结构 二叉树 二叉树,顾名思义,每个节点最多有两个“叉”,也就是两个子节点,分别是左子 节点和右子节点。不过,二叉树并不要求每个节点都有两个子节点,有的节点只 有左子节点,有的节点只有…...

智能分布式爬虫的数据处理流水线优化:基于深度强化学习的数据质量控制
在数字化浪潮席卷全球的今天,数据已成为企业和研究机构的核心资产。智能分布式爬虫作为高效的数据采集工具,在大规模数据获取中发挥着关键作用。然而,传统的数据处理流水线在面对复杂多变的网络环境和海量异构数据时,常出现数据质…...

docker 部署发现spring.profiles.active 问题
报错: org.springframework.boot.context.config.InvalidConfigDataPropertyException: Property spring.profiles.active imported from location class path resource [application-test.yml] is invalid in a profile specific resource [origin: class path re…...
