TDesign:Picker 选择器
Picker 选择器 API文档地址

单列选择器用法
/// view
onTap:(){TDPicker.showMultiPicker(context,data: [controller.coinList],title: '',rightTextStyle: TextStyle(color: AppColors.ColorMain),onConfirm: (selected) {controller.onTapCoin(selected);Navigator.of(context).pop();},);
},/// controller
List<String> coinList = ['BNB', 'BSC', 'ETH', 'USDT'];
// 切换coin
void onTapCoin(selected){var i = selected[0];print('选择的是${coinList[i]}');
}
相关文章:

TDesign:Picker 选择器
Picker 选择器 API文档地址 单列选择器用法 /// view onTap:(){TDPicker.showMultiPicker(context,data: [controller.coinList],title: ,rightTextStyle: TextStyle(color: AppColors.ColorMain),onConfirm: (selected) {controller.onTapCoin(selected);Navigator.of(contex…...

【AI赋能心理学论文创作策略】第十二章 AI辅助临床启示撰写指南
AI赋能心理学论文创作策略-系列文章目录 第十二章 AI辅助临床启示撰写指南 文章目录 AI赋能心理学论文创作策略-系列文章目录第十二章 AI辅助临床启示撰写指南 前言基础分析框架第一阶段:核心要素分析第二阶段:应用场景展开 关键环节提示第三阶段&#x…...

Pynsist 打包应用 和 PyWebIO 构建Web 应用
Pynsist:一键打包Python 应用代码为Windows 安装程序。 项目地址: https://github.com/takluyver/pynsist PyWebIO:为Python 开发者提供了一种快速、简洁的方式来创建Web 应用,无需学习前端技术 项目地址:https://g…...
git 使用配置
新拿到机器想配置git 获取代码权限,需要的配置方法 1. git 配置用户名和邮箱 git config --global user.name xxxgit config --global user.email xxemail.com 2. 生成ssh key ssh-keygen -t rsa -C "xxemail.com" 3. 获取ssh key cat ~/.ssh/id_rsa.…...
)
记一次Mysql的SELECT command denied to user...报错(非权限问题)
java.sql.SQLSyntaxErrorException: SELECT command denied to user ‘user_name’‘1.1.1.1’ for table ‘table_name’。错误信息的字面意思是:表“table_name”拒绝用户“user_name”“1.1.1.1”的SELECT命令 。 比较多的情况是:用户没有查看user表…...

element-plus的el-tree的双向绑定
el-tree改造了下 可选可取消 有默认值 不包含父级id 默认展开 点击节点也可触发选择 节点内容自定义 <template>{{ childKeys }}<!--default-checked-keys:默认展开值(正常来说需要包含父级id的 但是我们后端不要后端id )show-checkbox&#x…...
)
代码随想录-算法训练营day41(动态规划04:01背包,01背包滚动数组,分割等和子集)
第九章 动态规划part04● 01背包问题,你该了解这些! ● 01背包问题,你该了解这些! 滚动数组 ● 416. 分割等和子集 正式开始背包问题,背包问题还是挺难的,虽然大家可能看了很多背包问题模板代码…...
方法)
c#中context.SaveChanges()方法
跟踪实体的状态: Entity Framework 使用 Change Tracker 来跟踪上下文中所有实体的状态。实体的状态可以是: Added:新添加的实体(即将插入到数据库中)。Modified:已修改的实体(即将更新数据库中…...

李飞飞首个“空间智能”模型发布:一张图,生成一个3D世界 | LeetTalk Daily
“LeetTalk Daily”,每日科技前沿,由LeetTools AI精心筛选,为您带来最新鲜、最具洞察力的科技新闻。 在人工智能技术迅速发展的背景下,李飞飞创立的世界实验室于近期发布了首个“空间智能”模型,这一创新成果引发了3D生…...

Node.js简单接口实现教程
Node.js简单接口实现教程 1. 准备工作 确保您的计算机已安装: Node.js (建议版本16.x以上)npm (Node包管理器) 2. 项目初始化 # 创建项目目录 mkdir nodejs-api-tutorial cd nodejs-api-tutorial# 初始化npm项目 npm init -y# 安装必要依赖 npm install expres…...

AIGC 012-Video LDM-更进一步,SD作者将LDM扩展到视频生成任务!
AIGC 012-Video LDM-Stable Video diffusion前身,将LDM扩展到视频生成任务! 文章目录 0 论文工作1论文方法实验结果 0 论文工作 Video LDM作者也是Stable diffusion的作者,作者在SD的架构上进行扩展,实现了视频的生成。后续在Vid…...

windows文件下换行, linux上不换行 解决CR换行符替换为LF notepad++
html文件是用回车换行的,在windows电脑上,显示正常。 文件上传到linux服务器后,文件不换行了。只有一行。而且相关js插件也没法正常运行。 用notepad查看,显示尾部换行符,是CR,这就是原因。CR是不被识别的。…...
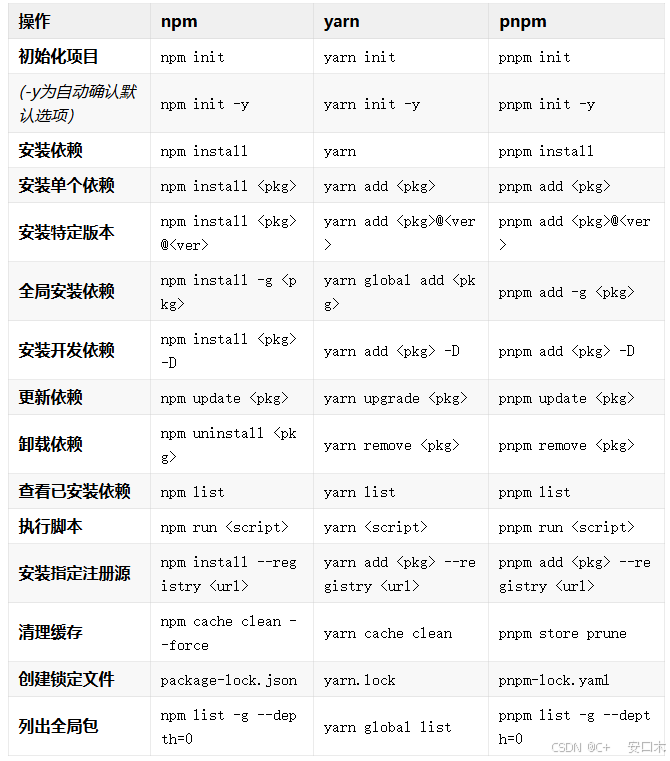
npm, yarn, pnpm之间的区别
前言 在现代化的开发中,一个人可能同时开发多个项目,安装的项目越来越多,所随之安装的依赖包也越来越臃肿,而且有时候所安装的速度也很慢,甚至会安装失败。 因此我们就需要去了解一下,我们的包管理器&#…...

静态链接和动态链接的特点
静态链接 链接方式:在编译时,所有依赖的库代码被直接打包到生成的可执行文件中。这意味着在程序运行时,不需要再加载任何外部库文件。 优点: 独立性强:生成的可执行文件可以在没有依赖库的系统上直接运行&am…...
Mac曲线救国实现Bandizip右键一级菜单
一、前言 个人认为:Bandizip是Mac上最好用的压缩软件,没有之一。 在Mac系统上,学习版的Bandizip由于签名检验问题无法在访达右键的一级菜单显示 解压相关菜单。 有能力的,希望还是支持正版,找找优惠渠道应该100左右。…...

进度与预算
一个项目,如果进度上可以按时完成,一般来说预算不会超标,或者超标幅度有限。 一个项目,如果进度上严重超期,预算基本上会超标,而且超标很大。 现在很多项目,人力成本占比都比较大,…...
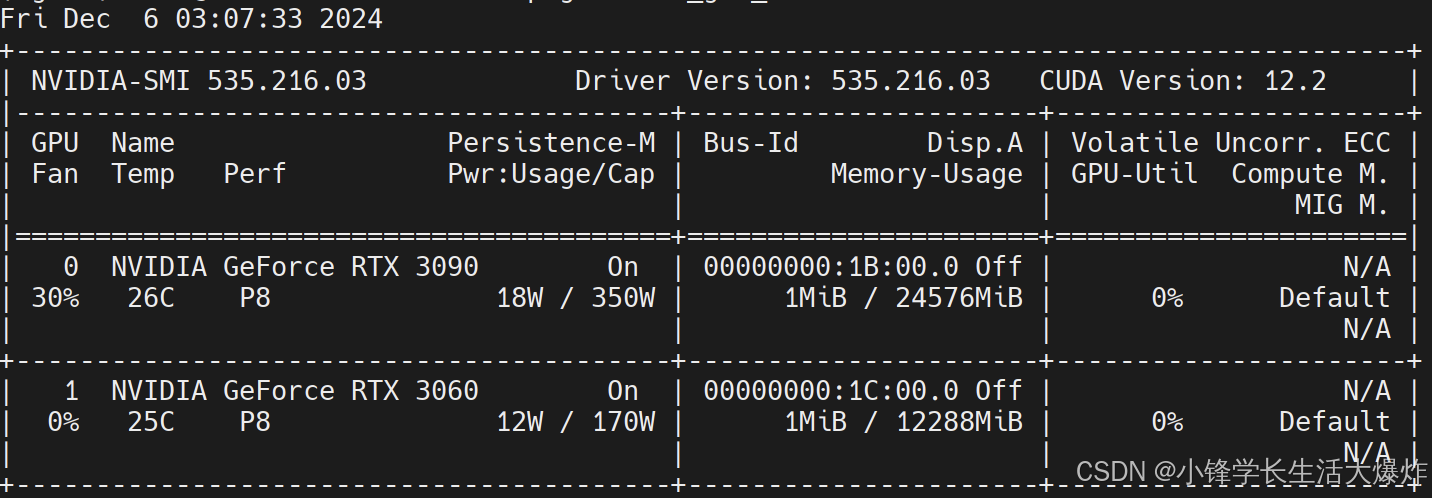
【教程】创建NVIDIA Docker共享使用主机的GPU
转载请注明出处:小锋学长生活大爆炸[xfxuezhagn.cn] 如果本文帮助到了你,欢迎[点赞、收藏、关注]哦~ 这套是我跑完整理的。直接上干货,复制粘贴即可! # 先安装toolkit sudo apt-get update sudo apt-get install -y ca-certifica…...
CEEMDAN-CPO-VMD二次分解(CEEMDAN+冠豪猪优化算法CPO优化VMD)
CEEMDAN-CPO-VMD二次分解(CEEMDAN冠豪猪优化算法CPO优化VMD) 目录 CEEMDAN-CPO-VMD二次分解(CEEMDAN冠豪猪优化算法CPO优化VMD)效果一览基本介绍程序设计参考资料 效果一览 基本介绍 首先运用CEEMDAN对数据进行一次分解ÿ…...

图论理论基础和存储方式的实现
图论1 图论 (Graph theory) 是数学的一个分支,图是图论的主要研究对象。图 (Graph) 是由若干给定的顶点及连接两顶点的边所构成的图形,这种图形通常用来描述某些事物之间的某种特定关系。顶点用于代表事物,连接两顶点的边则用于表示两个事物…...
自然数的序)
【实分析】【二】2.2 (c)自然数的序
文章目录 前言一、自然数的序的定义二、自然数的序的基本性质三、序的三歧性四、强归纳法原理总结 前言 在2.2 (b)的末尾,我们定义了自然数的正性,现在,我们来定义自然数的序,它是一种自然数的二元关系,通过加法进行定…...

【网络】每天掌握一个Linux命令 - iftop
在Linux系统中,iftop是网络管理的得力助手,能实时监控网络流量、连接情况等,帮助排查网络异常。接下来从多方面详细介绍它。 目录 【网络】每天掌握一个Linux命令 - iftop工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景…...

利用ngx_stream_return_module构建简易 TCP/UDP 响应网关
一、模块概述 ngx_stream_return_module 提供了一个极简的指令: return <value>;在收到客户端连接后,立即将 <value> 写回并关闭连接。<value> 支持内嵌文本和内置变量(如 $time_iso8601、$remote_addr 等)&a…...

大话软工笔记—需求分析概述
需求分析,就是要对需求调研收集到的资料信息逐个地进行拆分、研究,从大量的不确定“需求”中确定出哪些需求最终要转换为确定的“功能需求”。 需求分析的作用非常重要,后续设计的依据主要来自于需求分析的成果,包括: 项目的目的…...

RNN避坑指南:从数学推导到LSTM/GRU工业级部署实战流程
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文全面剖析RNN核心原理,深入讲解梯度消失/爆炸问题,并通过LSTM/GRU结构实现解决方案,提供时间序列预测和文本生成…...

网站指纹识别
网站指纹识别 网站的最基本组成:服务器(操作系统)、中间件(web容器)、脚本语言、数据厍 为什么要了解这些?举个例子:发现了一个文件读取漏洞,我们需要读/etc/passwd,如…...

浪潮交换机配置track检测实现高速公路收费网络主备切换NQA
浪潮交换机track配置 项目背景高速网络拓扑网络情况分析通信线路收费网络路由 收费汇聚交换机相应配置收费汇聚track配置 项目背景 在实施省内一条高速公路时遇到的需求,本次涉及的主要是收费汇聚交换机的配置,浪潮网络设备在高速项目很少,通…...

基于 TAPD 进行项目管理
起因 自己写了个小工具,仓库用的Github。之前在用markdown进行需求管理,现在随着功能的增加,感觉有点难以管理了,所以用TAPD这个工具进行需求、Bug管理。 操作流程 注册 TAPD,需要提供一个企业名新建一个项目&#…...

python爬虫——气象数据爬取
一、导入库与全局配置 python 运行 import json import datetime import time import requests from sqlalchemy import create_engine import csv import pandas as pd作用: 引入数据解析、网络请求、时间处理、数据库操作等所需库。requests:发送 …...

在 Spring Boot 中使用 JSP
jsp? 好多年没用了。重新整一下 还费了点时间,记录一下。 项目结构: pom: <?xml version"1.0" encoding"UTF-8"?> <project xmlns"http://maven.apache.org/POM/4.0.0" xmlns:xsi"http://ww…...

在树莓派上添加音频输入设备的几种方法
在树莓派上添加音频输入设备可以通过以下步骤完成,具体方法取决于设备类型(如USB麦克风、3.5mm接口麦克风或HDMI音频输入)。以下是详细指南: 1. 连接音频输入设备 USB麦克风/声卡:直接插入树莓派的USB接口。3.5mm麦克…...
