图论理论基础和存储方式的实现
图论1
图论 (Graph theory) 是数学的一个分支,图是图论的主要研究对象。图 (Graph) 是由若干给定的顶点及连接两顶点的边所构成的图形,这种图形通常用来描述某些事物之间的某种特定关系。顶点用于代表事物,连接两顶点的边则用于表示两个事物间具有这种关系。
1、图的理论基础
图(Graph)
用大写字母(如 G G G)表示图,通常记为 G = ( V , E ) G=(V,E) G=(V,E),其中 V V V 表示顶点集, E E E 表示边集。例如:设 G = ( V , E ) G=(V,E) G=(V,E) 是一个无向图, V V V 包含多个顶点, E E E 包含连接这些顶点的边。
相邻(Adjacent)
若顶点 u u u 和 v v v 相邻,可表示为: u ∼ v u \sim v u∼v。例如:在图 G G G 中,若顶点 u u u 和 v v v 之间有边相连,则有 u ∼ v u \sim v u∼v。
简单图(Simple Graph)
设 G = ( V , E ) G=(V,E) G=(V,E) 为简单图,特点是不存在自环(即不存在边 e = ( u , u ) e=(u,u) e=(u,u), u ∈ V u\in V u∈V)和多重边(任意两顶点间不存在多条相同边),可描述为: G = ( V , E ) G=(V,E) G=(V,E) 是简单图,满足无自环与多重边条件。
度数(Degree)
-
无向图中顶点度数:无向图里顶点 v v v 的度数用 deg ( v ) \deg(v) deg(v) 表示,比如:在无向图 G G G 中,顶点 v v v 的度数记为 deg ( v ) \deg(v) deg(v),其值等于与 v v v 相连的边的数量。
-
有向图中顶点度数:有向图中顶点 v v v 的入度表示为 indeg ( v ) \text{indeg}(v) indeg(v),出度表示为 outdeg ( v ) \text{outdeg}(v) outdeg(v)。例如:在有向图 G G G 中,顶点 v v v 的入度为 indeg ( v ) \text{indeg}(v) indeg(v),出度为 outdeg ( v ) \text{outdeg}(v) outdeg(v),度数可结合二者考量。
路径(Path)
用 P = ( v 0 , v 1 , ⋯ , v n ) P=(v_0,v_1,\cdots,v_n) P=(v0,v1,⋯,vn) 表示从顶点 v 0 v_0 v0 出发,依次经过 v 1 , ⋯ , v n v_1,\cdots,v_n v1,⋯,vn 这些顶点的路径。例如:在图 G G G 中,存在路径 P = ( v 1 , v 2 , v 3 ) P=(v_1,v_2,v_3) P=(v1,v2,v3),即从顶点 v 1 v_1 v1 出发,依次经过 v 2 v_2 v2 和 v 3 v_3 v3 的路线。
子图(Subgraph)
设 $G=(V,E)$ 是原图,$G'=(V',E')$ 是它的子图,关系表示为:$V'\subseteq V$ 且 $E'\subseteq E$,同时 $E'$ 中边的端点都在 $V'$ 中,则 $G'=(V',E')$ 为 $G$ 的子图。
比如:已知图 G = ( V , E ) G=(V,E) G=(V,E),取 V ′ V' V′ 为 V V V 的部分顶点集, E ′ E' E′ 为相应连接这些顶点的部分边集,满足条件后, G ′ = ( V ′ , E ′ ) G'=(V',E') G′=(V′,E′) 就是 G G G 的子图。
连通(Connected)
-
无向图连通:设 G = ( V , E ) G=(V,E) G=(V,E) 为无向图,若对任意 u , v ∈ V u,v\in V u,v∈V,都存在一条路径连接 u u u 和 v v v,则称 G G G 是连通的,可写成: ∀ u , v ∈ V \forall u,v\in V ∀u,v∈V,存在路径连接 u u u 与 v v v,则 G G G 连通。
-
有向图连通相关(强连通和弱连通):
-
强连通:对于有向图 G = ( V , E ) G=(V,E) G=(V,E),若对任意 u , v ∈ V u,v\in V u,v∈V,都存在从 u u u 到 v v v 的有向路径以及从 v v v 到 u u u 的有向路径,则 G G G 是强连通的,即: ∀ u , v ∈ V \forall u,v\in V ∀u,v∈V,存在从 u u u 到 v v v 及从 v v v 到 u u u 的有向路径,则 G G G 强连通。
-
弱连通:若把有向图 G = ( V , E ) G=(V,E) G=(V,E) 的边看作无向边时图是连通的,则 G G G 是弱连通的,表示为:将有向图 G = ( V , E ) G=(V,E) G=(V,E) 的边视为无向边时图连通,则 G G G 弱连通。
-
无向图(Undirected Graph)
直接用 $G=(V,E)$ 表示无向图,并说明其边无方向特点。
如: G = ( V , E ) G=(V,E) G=(V,E) 为无向图,其边没有方向,即对边 e = ( u , v ) ∈ E e=(u,v)\in E e=(u,v)∈E, u u u 与 v v v 的关系是对称的。
有向图(Directed Graph)
用 G = ( V , E ) G=(V,E) G=(V,E) 表示有向图,强调边有方向。
例如: G = ( V , E ) G=(V,E) G=(V,E) 为有向图,边 e = ( u , v ) ∈ E e=(u,v)\in E e=(u,v)∈E 有方向,从 u u u 指向 v v v,表示一种单向关系。
割(Cut)
-
边割(针对无向图):设 G = ( V , E ) G=(V,E) G=(V,E) 是连通无向图,若存在边子集 E ′ ⊆ E E'\subseteq E E′⊆E,去掉 E ′ E' E′ 后使得图不再连通,则 E ′ E' E′ 是 G G G 的一个边割,可表示为: G = ( V , E ) G=(V,E) G=(V,E) 连通无向图, ∃ E ′ ⊆ E \exists E'\subseteq E ∃E′⊆E,去掉 E ′ E' E′ 后 G G G 不连通,则 E ′ E' E′ 为 G G G 的边割。
-
点割(针对无向图):对于连通无向图 G = ( V , E ) G=(V,E) G=(V,E),若存在顶点子集 V ′ ⊆ V V'\subseteq V V′⊆V,去掉 V ′ V' V′ 以及和这些顶点相关联的边后使得图不再连通,则 V ′ V' V′ 是 G G G 的一个点割,写成: G = ( V , E ) G=(V,E) G=(V,E) 连通无向图, ∃ V ′ ⊆ V \exists V'\subseteq V ∃V′⊆V,去掉 V ′ V' V′ 及相关边后 G G G 不连通,则 V ′ V' V′ 为 G G G 的点割。
稀疏图/稠密图(Sparse Graph / Dense Graph)
-
稀疏图:对于图 G = ( V , E ) G=(V,E) G=(V,E),若 ∣ E ∣ ≪ ∣ V ∣ 2 |E| \ll |V|^2 ∣E∣≪∣V∣2(这里 ≪ \ll ≪ 示意边数量远小于顶点数量平方的大概关系),则 G G G 为稀疏图,如: G = ( V , E ) G=(V,E) G=(V,E),当 ∣ E ∣ ≪ ∣ V ∣ 2 |E| \ll |V|^2 ∣E∣≪∣V∣2 时, G G G 为稀疏图。
-
稠密图:与稀疏图对应,若 ∣ E ∣ |E| ∣E∣ 接近 ∣ V ∣ 2 |V|^2 ∣V∣2 量级,可写成: G = ( V , E ) G=(V,E) G=(V,E),当 ∣ E ∣ |E| ∣E∣ 接近 ∣ V ∣ 2 |V|^2 ∣V∣2 时, G G G 为稠密图。
补图(Complement Graph)
设 G = ( V , E ) G=(V,E) G=(V,E) 是无向简单图,其补图 G ‾ = ( V , E ‾ ) \overline{G}=(V,\overline{E}) G=(V,E),其中 E ‾ \overline{E} E 包含了所有不在 E E E 中但两端点在 V V V 中的边,可表示为: G = ( V , E ) G=(V,E) G=(V,E) 为无向简单图,其补图 G ‾ = ( V , E ‾ ) \overline{G}=(V,\overline{E}) G=(V,E), E ‾ = { ( u , v ) ∣ u , v ∈ V , ( u , v ) ∉ E } \overline{E}=\{(u,v)\mid u,v\in V,(u,v)\notin E\} E={(u,v)∣u,v∈V,(u,v)∈/E}。
反图(Inverse Graph)
对于有向图 G = ( V , E ) G=(V,E) G=(V,E),其反图 G − 1 = ( V , E − 1 ) G^{-1}=(V,E^{-1}) G−1=(V,E−1),这里 E − 1 E^{-1} E−1 是把 E E E 中每条边的方向都反转所得到的边集,写成: G = ( V , E ) G=(V,E) G=(V,E) 为有向图,其反图 G − 1 = ( V , E − 1 ) G^{-1}=(V,E^{-1}) G−1=(V,E−1), E − 1 = { ( v , u ) ∣ ( u , v ) ∈ E } E^{-1}=\{(v,u)\mid (u,v)\in E\} E−1={(v,u)∣(u,v)∈E}。
特殊的图
完全图(Complete Graph):
- 无向完全图:用 K n K_n Kn 表示 n n n 个顶点的无向完全图,其边数为 n ( n − 1 ) 2 \frac{n(n - 1)}{2} 2n(n−1)。例如: K 5 K_5 K5 是有 5 5 5 个顶点的无向完全图,边数为 5 × ( 5 − 1 ) 2 = 10 \frac{5\times(5 - 1)}{2}=10 25×(5−1)=10。
- 有向完全图:用 D n D_n Dn 表示 n n n 个顶点的有向完全图,其边数为 n ( n − 1 ) n(n - 1) n(n−1)。
- 树(Tree):树可描述为无向连通且无环的图,记为: T = ( V , E ) T=(V,E) T=(V,E) 为树,即 T T T 是无向连通且无环的图。
- 二分图(Bipartite Graph):设顶点集 V V V 可分成两个互不相交的子集 V 1 V_1 V1 和 V 2 V_2 V2,使图中每条边的两个端点分别属于 V 1 V_1 V1 和 V 2 V_2 V2,可写成: G = ( V , E ) G=(V,E) G=(V,E) 为二分图, ∃ V 1 , V 2 ⊆ V \exists V_1,V_2\subseteq V ∃V1,V2⊆V, V 1 ∩ V 2 = ∅ V_1\cap V_2=\varnothing V1∩V2=∅,且 ∀ e = ( u , v ) ∈ E \forall e=(u,v)\in E ∀e=(u,v)∈E, u ∈ V 1 u\in V_1 u∈V1 且 v ∈ V 2 v\in V_2 v∈V2 或 u ∈ V 2 u\in V_2 u∈V2 且 v ∈ V 1 v\in V_1 v∈V1。
同构(Isomorphism)
设 G = ( V , E ) G=(V,E) G=(V,E) 和 G ′ = ( V ′ , E ′ ) G'=(V',E') G′=(V′,E′) 是两个图,若存在双射函数 f : V → V ′ f: V \to V' f:V→V′,使得对于任意的 u , v ∈ V u,v \in V u,v∈V, ( u , v ) ∈ E (u,v) \in E (u,v)∈E 当且仅当 ( f ( u ) , f ( v ) ) ∈ E ′ (f(u),f(v)) \in E' (f(u),f(v))∈E′,则称 G G G 和 G ′ G' G′ 是同构的,表示为: G = ( V , E ) G=(V,E) G=(V,E), G ′ = ( V ′ , E ′ ) G'=(V',E') G′=(V′,E′),若 ∃ f : V → V ′ \exists f: V \to V' ∃f:V→V′ 双射,满足 ∀ u , v ∈ V \forall u,v\in V ∀u,v∈V, ( u , v ) ∈ E ⇔ ( f ( u ) , f ( v ) ) ∈ E ′ (u,v)\in E \Leftrightarrow (f(u),f(v))\in E' (u,v)∈E⇔(f(u),f(v))∈E′,则 G G G 与 G ′ G' G′ 同构。
无向简单图的二元运算
并运算(Union):设 G 1 = ( V 1 , E 1 ) G_1=(V_1,E_1) G1=(V1,E1) 和 G 2 = ( V 2 , E 2 ) G_2=(V_2,E_2) G2=(V2,E2) 是两个无向简单图,它们的并 G 1 ∪ G 2 = ( V 1 ∪ V 2 , E 1 ∪ E 2 ) G_1\cup G_2=(V_1\cup V_2, E_1\cup E_2) G1∪G2=(V1∪V2,E1∪E2),可写成: G 1 = ( V 1 , E 1 ) G_1=(V_1,E_1) G1=(V1,E1), G 2 = ( V 2 , E 2 ) G_2=(V_2,E_2) G2=(V2,E2),则 G 1 ∪ G 2 = ( V 1 ∪ V 2 , E 1 ∪ E 2 ) G_1\cup G_2=(V_1\cup V_2, E_1\cup E_2) G1∪G2=(V1∪V2,E1∪E2)。例如:已知 G 1 G_1 G1 和 G 2 G_2 G2 两个无向简单图,计算它们的并图 G 1 ∪ G 2 G_1\cup G_2 G1∪G2。
交运算(Intersection): G 1 ∩ G 2 = ( V 1 ∩ V 2 , E 1 ∩ E 2 ) G_1\cap G_2=(V_1\cap V_2, E_1\cap E_2) G1∩G2=(V1∩V2,E1∩E2),表示为: G 1 = ( V 1 , E 1 ) G_1=(V_1,E_1) G1=(V1,E1), G 2 = ( V 2 , E 2 ) G_2=(V_2,E_2) G2=(V2,E2),则 G 1 ∩ G 2 = ( V 1 ∩ V 2 , E 1 ∩ E 2 ) G_1\cap G_2=(V_1\cap V_2, E_1\cap E_2) G1∩G2=(V1∩V2,E1∩E2)。
差运算(Difference): G 1 − G 2 = ( V 1 , E 1 − E 2 ) G_1 - G_2=(V_1, E_1 - E_2) G1−G2=(V1,E1−E2),写成: G 1 = ( V 1 , E 1 ) G_1=(V_1,E_1) G1=(V1,E1), G 2 = ( V 2 , E 2 ) G_2=(V_2,E_2) G2=(V2,E2),则 G 1 − G 2 = ( V 1 , E 1 − E 2 ) G_1 - G_2=(V_1, E_1 - E_2) G1−G2=(V1,E1−E2)。
特殊的点集/边集
支配集(Dominating Set)
在无向图 G = ( V , E ) G=(V,E) G=(V,E) 中,顶点子集 D ⊆ V D\subseteq V D⊆V 称为支配集,若对任意顶点 v ∈ V − D v\in V - D v∈V−D,都存在顶点 u ∈ D u\in D u∈D 使得 u u u 和 v v v 相邻,可表示为: G = ( V , E ) G=(V,E) G=(V,E) 无向图, ∃ D ⊆ V \exists D\subseteq V ∃D⊆V, ∀ v ∈ V − D \forall v\in V - D ∀v∈V−D, ∃ u ∈ D \exists u\in D ∃u∈D, u ∼ v u \sim v u∼v,则 D D D 为支配集。
边支配集(Edge Dominating Set)
在无向图 G = ( V , E ) G=(V,E) G=(V,E) 中,边子集 F ⊆ E F\subseteq E F⊆E 称为边支配集,若对任意边 e ∈ E − F e\in E - F e∈E−F,都存在边 f ∈ F f\in F f∈F 与 e e e 相邻(共享端点),写成: G = ( V , E ) G=(V,E) G=(V,E) 无向图, ∃ F ⊆ E \exists F\subseteq E ∃F⊆E, ∀ e ∈ E − F \forall e\in E - F ∀e∈E−F, ∃ f ∈ F \exists f\in F ∃f∈F, e e e 与 f f f 共享端点,则 F F F 为边支配集。
独立集(Independent Set)
在无向图 G = ( V , E ) G=(V,E) G=(V,E) 中,顶点子集 I ⊆ V I\subseteq V I⊆V 称为独立集,若 I I I 中任意两个顶点都不相邻,即: G = ( V , E ) G=(V,E) G=(V,E) 无向图, ∃ I ⊆ V \exists I\subseteq V ∃I⊆V, ∀ u , v ∈ I \forall u,v\in I ∀u,v∈I, u u u 与 v v v 不相邻,则 I I I 为独立集。
匹配(Matching)
在无向图 G = ( V , E ) G=(V,E) G=(V,E) 中,边子集 M ⊆ E M\subseteq E M⊆E 称为匹配,若 M M M 中的边两两之间没有公共端点,可表示为: G = ( V , E ) G=(V,E) G=(V,E) 无向图, ∃ M ⊆ E \exists M\subseteq E ∃M⊆E, ∀ e 1 , e 2 ∈ M \forall e_1,e_2\in M ∀e1,e2∈M, e 1 e_1 e1 与 e 2 e_2 e2 无公共端点,则 M M M 为匹配。
点覆盖(Vertex Cover)
在无向图 G = ( V , E ) G=(V,E) G=(V,E) 中,顶点子集 C ⊆ V C\subseteq V C⊆V 称为点覆盖,若图 G G G 中的每条边至少有一个端点在 C C C 中,写成: G = ( V , E ) G=(V,E) G=(V,E) 无向图, ∃ C ⊆ V \exists C\subseteq V ∃C⊆V, ∀ e ∈ E \forall e\in E ∀e∈E, ∃ v ∈ C \exists v\in C ∃v∈C, v v v 为 e e e 的端点,则 C C C 为点覆盖。
边覆盖(Edge Cover)
在无向图 G = ( V , E ) G=(V,E) G=(V,E) 中,边子集 L ⊆ E L\subseteq E L⊆E 称为边覆盖,若对于任意顶点 v ∈ V v\in V v∈V,都存在边 e ∈ L e\in L e∈L 使得 v v v 是 e e e 的端点,可表示为: G = ( V , E ) G=(V,E) G=(V,E) 无向图, ∃ L ⊆ E \exists L\subseteq E ∃L⊆E, ∀ v ∈ V \forall v\in V ∀v∈V, ∃ e ∈ L \exists e\in L ∃e∈L, v v v 为 e e e 的端点,则 L L L 为边覆盖。
团(Clique)
在无向图 G = ( V , E ) G=(V,E) G=(V,E) 中,顶点子集 K ⊆ V K\subseteq V K⊆V 称为团,若 K K K 中任意两个顶点都相邻,即 K K K 所诱导出的子图是完全图,可表示为: G = ( V , E ) G=(V,E) G=(V,E) 无向图, ∃ K ⊆ V \exists K\subseteq V ∃K⊆V, ∀ u , v ∈ K \forall u,v\in K ∀u,v∈K, u ∼ v u \sim v u∼v,则 K K K 为团。
图的矩阵表示(存储方式)
邻接矩阵(Adjacency Matrix)
对于一个无向图 G = ( V , E ) G=(V,E) G=(V,E) ,设顶点集 V = { v 1 , v 2 , ⋯ , v n } V = \{v_1, v_2, \cdots, v_n\} V={v1,v2,⋯,vn},其邻接矩阵 A A A 是一个 n × n n\times n n×n 的矩阵,其中元素 a i j a_{ij} aij 定义为:若顶点 v i v_i vi 和 v j v_j vj 相邻,则 a i j = 1 a_{ij} = 1 aij=1(对于无向简单图);若不相邻,则 a i j = 0 a_{ij} = 0 aij=0。
用公式表示为: a i j = { 1 , v i ∼ v j 相邻 0 , v i ∼ v j 不相邻 a_{ij} = \begin{cases}1, & v_i \sim v_j\text{相邻} \\ 0, & v_i \sim v_j\text{不相邻}\end{cases} aij={1,0,vi∼vj相邻vi∼vj不相邻
例如,对于一个简单的三角形形状的无向图,其邻接矩阵为: ( 0 1 1 1 0 1 1 1 0 ) \begin{pmatrix}0 & 1 & 1 \\ 1 & 0 & 1 \\ 1 & 1 & 0\end{pmatrix} 011101110 。
对于有向图,若存在从顶点 v i v_i vi 指向 v j v_j vj 的边,则 a i j = 1 a_{ij} = 1 aij=1,否则 a i j = 0 a_{ij} = 0 aij=0。其邻接矩阵能反映出有向图中顶点之间的有向连接关系。
关联矩阵(Incidence Matrix)
设无向图 G = ( V , E ) G=(V,E) G=(V,E) ,顶点集 V = { v 1 , v 2 , ⋯ , v n } V = \{v_1, v_2, \cdots, v_n\} V={v1,v2,⋯,vn},边集 E = { e 1 , e 2 , ⋯ , e m } E = \{e_1, e_2, \cdots, e_m\} E={e1,e2,⋯,em},其关联矩阵 M M M 是一个 n × m n\times m n×m 的矩阵,元素 m i j m_{ij} mij 定义如下:若顶点 v i v_i vi 与边 e j e_j ej 关联(即 v i v_i vi 是 e j e_j ej 的一个端点),则 m i j = 1 m_{ij} = 1 mij=1;若不关联,则 m i j = 0 m_{ij} = 0 mij=0。
用公式表示为: m i j = { 1 , 如果 v i 关联 e j 0 , 如果 v i 不关联 e j m_{ij} = \begin{cases}1, & \text{如果} v_i \text{关联} e_j \\ 0, & \text{如果} v_i \text{不关联} e_j\end{cases} mij={1,0,如果vi关联ej如果vi不关联ej
例如,对于一个简单的有四条边、三个顶点的无向图,其关联矩阵可能为: ( 1 1 0 0 1 0 1 1 0 1 1 0 ) \begin{pmatrix}1 & 1 & 0 & 0 \\ 1 & 0 & 1 & 1 \\ 0 & 1 & 1 & 0\end{pmatrix} 110101011010 。 有向图的关联矩阵定义稍有不同,对于有向边 e j e_j ej ,若顶点 v i v_i vi 是边 e j e_j ej 的起点,则 m i j = 1 m_{ij} = 1 mij=1;若 v i v_i vi 是边 e j e_j ej 的终点,则 m i j = − 1 m_{ij} = -1 mij=−1;若 v i v_i vi 与 e j e_j ej 不关联,则 m i j = 0 m_{ij} = 0 mij=0。
2、图的存储
n为图的顶点数,m为图的边数, d + ( u ) d^+(u) d+(u)为点u的出度, d − ( u ) d^-(u) d−(u)为点u的入度
2.1、直接存边
实现:
使用多个数组来存储变得起点终点和权值。
复杂度:
查询是否存在某条边: O ( m ) O(m) O(m)
遍历一个点的所有出边: O ( m ) O(m) O(m)
遍历整张图: O ( n m ) O(nm) O(nm)
空间复杂度: O ( m ) O(m) O(m)
注:在Kruskal算法中,需要把边按权值排序,需要直接存储边。
2.2、邻接矩阵
实现:
使用二维数组 a d j [ u ] [ v ] adj[u][v] adj[u][v] 来存储, a d j [ u ] [ v ] adj[u][v] adj[u][v]的值表示 u u u 到 v v v 是否有边。
用公式表示为: a d j [ u ] [ v ] = { 1 , 存在 u 到 v 的边 0 , 不存在 u 到 v 的边 adj[u][v]= \left\{\begin{matrix} 1 &,存在u到v的边\\ 0 &,不存在u到v的边 \end{matrix}\right. adj[u][v]={10,存在u到v的边,不存在u到v的边
代码
复杂度:
查询是否存在某条边: O ( 1 ) O(1) O(1)
遍历一个点的所有出边: O ( n ) O(n) O(n)
遍历整张图: O ( n 2 ) O(n^2) O(n2)
空间复杂度: O ( n 2 ) O(n^2) O(n2)
邻接矩阵只适用于没有重边的图
由于邻接矩阵在稀疏图上效率很低(尤其是在点数较多的图上,空间无法承受),所以一般只会在稠密图上使用邻接矩阵。
2.3、邻接表
2.4、链式前向星
相关文章:

图论理论基础和存储方式的实现
图论1 图论 (Graph theory) 是数学的一个分支,图是图论的主要研究对象。图 (Graph) 是由若干给定的顶点及连接两顶点的边所构成的图形,这种图形通常用来描述某些事物之间的某种特定关系。顶点用于代表事物,连接两顶点的边则用于表示两个事物…...
自然数的序)
【实分析】【二】2.2 (c)自然数的序
文章目录 前言一、自然数的序的定义二、自然数的序的基本性质三、序的三歧性四、强归纳法原理总结 前言 在2.2 (b)的末尾,我们定义了自然数的正性,现在,我们来定义自然数的序,它是一种自然数的二元关系,通过加法进行定…...
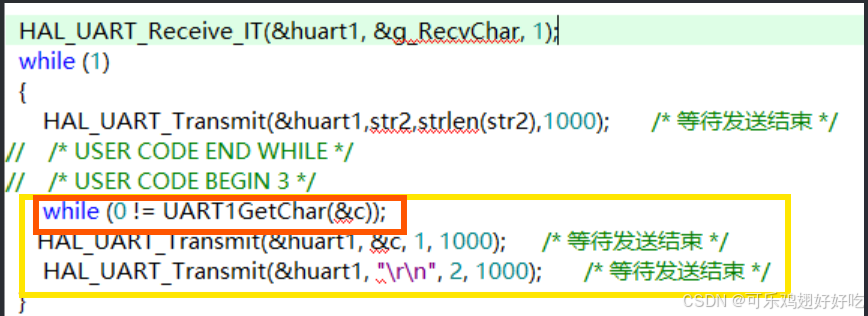
STM32串口接收与发送(关于为什么接收不需要中断而发生需要以及HAL_UART_Transmit和HAL_UART_Transmit_IT的区别)
一、HAL_UART_Transmit和HAL_UART_Transmit_IT的区别 1. HAL_UART_Transmit_IT(非阻塞模式): HAL_UART_Transmit_IT 是非阻塞的传输函数,也就是说,当你调用 HAL_UART_Transmit_IT 时,它不会等到数据完全发…...

k8s 之storageclass使用nfs动态申请PV
文章目录 配置角色权限部署nfs-client-provisioner创建 NFS StorageClass创建 PVC 来动态申请 PV在 Pod 中使用 PVC验证存储是否正确挂载使用 kubectl 和 jq 筛选 PVCwaiting for a volume to be created, either by external provisioner "nfs-diy" or manually cre…...
功能)
vue移动端实现下载(截图)功能
前言 通过html2canvas实现截图功能然后保存 简介 html2canvas库允许我们直接在浏览器上拍摄网页或部分网页的“截图”,即浏览器实现截图的功能。 原理 屏幕截图是基于DO的。其基本原理就是读取已经渲染好的DOM元素的结构和样式信息,然后基于这些信息…...

【Golang】Golang基础语法之面向对象:结构体和方法
面向对象——结构 Go 仅支持封装,不支持继承和多态;继承和多态要做的事情交给接口来完成,即——面向接口编程。Go 只有 struct,没有 class。 定义一个最简单的树节点(treeNode)结构,方法如下&…...
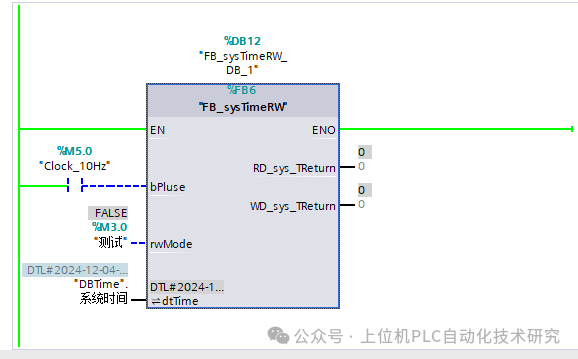
【西门子PLC.博途】——在S71200里写时间设置和读取功能块
之前我们在这篇文章中介绍过如何读取PLC的系统时间。我们来看看在西门子1200里面有什么区别。同时也欢迎关注gzh。 我们在S71200的帮助文档中搜索时间后找到这个数据类型 在博途中他是一个结构体,具体为 然后我们再看看它带的读取和写入时间块 读取时间࿱…...

位运算(一)位运算简单总结
191. 位1的个数 给定一个正整数 n,编写一个函数,获取一个正整数的二进制形式并返回其二进制表达式中 设置位 的个数(也被称为 汉明重量)。 示例 1: 输入:n 11 输出:3 解释:输入的二…...

工厂方法模式的理解和实践
在软件开发中,设计模式是一种经过验证的解决特定问题的通用方案。工厂方法模式(Factory Method Pattern)是创建型设计模式之一,它提供了一种创建对象的接口,但由子类决定要实例化的类是哪一个。工厂方法让类的实例化推…...
)
C# 设计模式--观察者模式 (Observer Pattern)
定义 观察者模式是一种行为设计模式,它定义了对象之间的一对多依赖关系,当一个对象的状态发生改变时,所有依赖于它的对象都会得到通知并自动更新。观察者模式的核心在于解耦主题(被观察者)和观察者之间的依赖关系。 …...
介绍)
【开发语言】层次状态机(HSM)介绍
层次状态机(Hierarchical State Machine, HSM),从基本原理、结构设计、实现方法以及如何结合 Qt 进行具体实现等方面进行分析。 1. 层次状态机的基本原理 层次状态机是一种用于管理复杂系统行为的状态机模型,它通过将状态组织成…...

03-13、SpringCloud Alibaba第十三章,升级篇,服务降级、熔断和限流Sentinel
SpringCloud Alibaba第十三章,升级篇,服务降级、熔断和限流Sentinel 一、Sentinel概述 1、Sentinel是什么 随着微服务的流行,服务和服务之间的稳定性变得越来越重要。Sentinel 以流量为切入点,从流量控制、熔断降级、系统负载保…...

【k8s 深入学习之 event 聚合】event count累记聚合(采用 Patch),Message 聚合形成聚合 event(采用Create)
参考 15.深入k8s:Event事件处理及其源码分析 - luozhiyun - 博客园event 模块总览 EventRecorder:是事件生成者,k8s组件通过调用它的方法来生成事件;EventBroadcaster:事件广播器,负责消费EventRecorder产生的事件,然后分发给broadcasterWatcher;broadcasterWatcher:用…...

leetcode104.二叉树的最大深度
给定一个二叉树 root ,返回其最大深度。 二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数。 示例 1: 输入:root [3,9,20,null,null,15,7] 输出:3示例 2: 输入:root [1,null,2] 输出…...
)
蓝桥杯2117砍竹子(简单易懂 包看包会版)
问题描述 这天, 小明在砍竹子, 他面前有 n 棵竹子排成一排, 一开始第 i 棵竹子的 高度为 hi. 他觉得一棵一棵砍太慢了, 决定使用魔法来砍竹子。魔法可以对连续的一 段相同高度的竹子使用, 假设这一段竹子的高度为 H, 那么 用一次魔法可以 把这一段竹子的高度都变为 ⌊H2⌋…...

LCD与lvgl
LCD与lvgl 目录 LCD与lvgl 回顾 LCD 的驱动层讲解 1、LCD 的常见接口 2、我们的 LCD 的参数 3、LCD 的设备树说明 4、LCD 的设备树说明 5、如何移植 LCD 的驱动(重点) LCD 的应用层开发 1:LCD 应用开发->界面开发的方法 2:LVGL 模拟器安装 3:LVGL 工程创建和…...

SpringBoot 赋能:精铸超稳会员制医疗预约系统,夯实就医数据根基
1绪论 1.1开发背景 传统的管理方式都在使用手工记录的方式进行记录,这种方式耗时,而且对于信息量比较大的情况想要快速查找某一信息非常慢,对于会员制医疗预约服务信息的统计获取比较繁琐,随着网络技术的发展,采用电脑…...
android studio 读写文件操作(应用场景二)
android studio版本:2023.3.1 patch2 例程:readtextviewIDsaveandread 本例程是个过渡例程,如果单是实现下图的目的有更简单的方法,但这个方法是下一步工作的基础,所以一定要做。 例程功能:将两个textvi…...

小尺寸低功耗蓝牙模块在光伏清扫机器人上的应用
一、引言 随着可再生能源的迅速发展,光伏发电系统的清洁与维护变得越来越重要。光伏清扫机器人通过自动化技术提高了清洁效率,而蓝牙模组的集成为这些设备提供了更为智能的管理和控制方案。 二、蓝牙模组的功能与实现: 蓝牙模组ANS-BT103M…...

防火墙有什么作用
防火墙的作用:1. 提供网络安全防护;2. 实施访问控制和流量过滤;3. 检测和阻止恶意攻击;4. 保护内部网络免受未经授权的访问;5. 监控网络流量和安全事件;6. 支持虚拟专用网络(VPN)。防…...

Linux相关概念和易错知识点(42)(TCP的连接管理、可靠性、面临复杂网络的处理)
目录 1.TCP的连接管理机制(1)三次握手①握手过程②对握手过程的理解 (2)四次挥手(3)握手和挥手的触发(4)状态切换①挥手过程中状态的切换②握手过程中状态的切换 2.TCP的可靠性&…...

P3 QT项目----记事本(3.8)
3.8 记事本项目总结 项目源码 1.main.cpp #include "widget.h" #include <QApplication> int main(int argc, char *argv[]) {QApplication a(argc, argv);Widget w;w.show();return a.exec(); } 2.widget.cpp #include "widget.h" #include &q…...

spring:实例工厂方法获取bean
spring处理使用静态工厂方法获取bean实例,也可以通过实例工厂方法获取bean实例。 实例工厂方法步骤如下: 定义实例工厂类(Java代码),定义实例工厂(xml),定义调用实例工厂ÿ…...
)
相机Camera日志分析之三十一:高通Camx HAL十种流程基础分析关键字汇总(后续持续更新中)
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了:有对最普通的场景进行各个日志注释讲解,但相机场景太多,日志差异也巨大。后面将展示各种场景下的日志。 通过notepad++打开场景下的日志,通过下列分类关键字搜索,即可清晰的分析不同场景的相机运行流程差异…...
集成 Mybatis-Plus 和 Mybatis-Plus-Join)
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join 1、依赖1.1、依赖版本1.2、pom.xml 2、代码2.1、SqlSession 构造器2.2、MybatisPlus代码生成器2.3、获取 config.yml 配置2.3.1、config.yml2.3.2、项目配置类 2.4、ftl 模板2.4.1、…...

AI+无人机如何守护濒危物种?YOLOv8实现95%精准识别
【导读】 野生动物监测在理解和保护生态系统中发挥着至关重要的作用。然而,传统的野生动物观察方法往往耗时耗力、成本高昂且范围有限。无人机的出现为野生动物监测提供了有前景的替代方案,能够实现大范围覆盖并远程采集数据。尽管具备这些优势…...

接口自动化测试:HttpRunner基础
相关文档 HttpRunner V3.x中文文档 HttpRunner 用户指南 使用HttpRunner 3.x实现接口自动化测试 HttpRunner介绍 HttpRunner 是一个开源的 API 测试工具,支持 HTTP(S)/HTTP2/WebSocket/RPC 等网络协议,涵盖接口测试、性能测试、数字体验监测等测试类型…...

python爬虫——气象数据爬取
一、导入库与全局配置 python 运行 import json import datetime import time import requests from sqlalchemy import create_engine import csv import pandas as pd作用: 引入数据解析、网络请求、时间处理、数据库操作等所需库。requests:发送 …...

elementUI点击浏览table所选行数据查看文档
项目场景: table按照要求特定的数据变成按钮可以点击 解决方案: <el-table-columnprop"mlname"label"名称"align"center"width"180"><template slot-scope"scope"><el-buttonv-if&qu…...

DBLP数据库是什么?
DBLP(Digital Bibliography & Library Project)Computer Science Bibliography是全球著名的计算机科学出版物的开放书目数据库。DBLP所收录的期刊和会议论文质量较高,数据库文献更新速度很快,很好地反映了国际计算机科学学术研…...
