当前位置： 首页 > news >正文

Android 第三方框架：RxJava：源码分析：责任链模式

news 2026/2/11 0:02:43

文章目录

    • 责任链模式
    • RxJava中的责任链
    • 总结

责任链模式

RxJava中的责任链

链式调用的使用过程中形成了两个单向链表

第一个单向链表是Observable链表

它的形成过程：

1.首先调用Observable的静态方法创建第一个Observable对象，作为Observable链表的表尾

2.调用当前的Observable对象的实例方法，创建新的Observable对象，新的Observable对象持有当前Observable对象，向Observable链表添加表头，

3.最后调用Observable对象的subscribe方法，Observable链表创建完成

Observable链表用于传递Observer对象，创建Observer链表

第二个单向链表是Observer链表

它的形成过程：

1.最后调用Observable对象的subscribe方法，传入Observer对象，创建新的Observer对象、将传入的Observer对象封装在其中，并交给Observable链表中的上一个Observable对象

2.直到传给Observable链表中的第一个Observable，Observer链表创建完成

Observer链表用于处理数据，它的处理过程：

1.第一个Observable对象将数据交给Observer链表处理，Observer链表中的Observer对象处理数据，将处理后的结果传递给下一个Observer对象，直到最后一个Observer对象

总结

相关文章：

Android 第三方框架：RxJava：源码分析：责任链模式

文章目录 责任链模式RxJava中的责任链总结 责任链模式 RxJava中的责任链 链式调用的使用过程中形成了两个单向链表 第一个单向链表是Observable链表 它的形成过程： 1.首先调用Observable的静态方法创建第一个Observable对象，作为Observable链表的表…...

编程日记 2024/12/13 5:41:02

网络安全 与 加密算法

计算机中的网络安全 在本篇中介绍了以下几个方面: 机密性 密码学 对称加密算法(DES, 3DES, AES) 公开秘钥算法 RSA大素数的获取 完整性 散列函数(MD5, SHA-1, 并没有提及算法实现) 报文鉴别(MAC) 数字签名 端点鉴别 应用 SSL(TCP网络安全) 运行时安全 防火墙的基本知识 …...

编程日记 2024/12/13 5:40:01

UE4_贴花_贴花基础知识二

五、多表面投射 在本示例中，你将了解贴花如何在多个表面上进行投射。请注意，如果表面朝向与投射方向较为平行，贴花投射时必然会产生一些拉伸。另外，请记住，贴花可以在包括骨骼网格体在内的静态和动态网格体上进行投射。…...

编程日记 2024/12/13 5:39:00

ElasticSearch 搜索、排序、分页功能

一、DSL 查询文档 ElasticSearch 的查询依然是基于 json 风格的 DSL 来实现的。 官方文档：https://www.elastic.co/guide/en/elasticsearch/reference/8.15/query-dsl.html 1.1 DSL 查询分类 常见的查询类型包括： 查询所有：查询出所有数…...

编程日记 2024/12/13 5:37:59

MySQL-9.1.0 实现最基础的主从复制

目录 1 实验介绍 2 实验准备 2.1 创建目录为MySQL挂载使用 2.2 编写 docker-compose.yml 文件 2.3 启动容器 3 主从复制操作 3.1 MASTER 操作指令 3.2 SLAVE1 操作指令 3.3 SLAVE2 操作指令 4 验证是否实现主从 4.1 导入sql脚本查看是否正常主从复制 4.2 检验从库是否看见复制…...

编程日记 2024/12/13 5:33:55

Java中的“泛型“

泛型（Generics）是Java中的一种重要特性，它允许在定义类、接口和方法时使用类型参数（type parameters）。泛型的主要目的是提高代码的类型安全性和重用性。下面我将详细讲解Java中的泛型。 1. 泛型的基本概念 泛型允许我…...

编程日记 2024/12/13 5:32:54

前端（五）css属性

css属性 文章目录 css属性一、字体属性二、文本属性三、背景属性四、盒子模型 一、字体属性 font-weight：文字粗细，在100到900之间，normal(400),bord(700),inherit(继承父类) font-style：文字风格，normal表示正常(默认…...

编程日记 2024/12/13 5:30:52

总结拓展十七：SAP 采购订单行项目“交货“页签解析

《 SAP采购订单行项目“交货”页签字段解析》 在 SAP 系统的采购流程中，采购订单行项目的“交货”页签承载着关键的信息，其中的字段更是对整个交货环节的精准描述和把控的重要元素。理解和正确解析这些字段，对于确保采购流程的顺利进行、优化…...

编程日记 2024/12/13 5:25:41

分布式日志系统设计

一、分布式日志系统定义 分布式日志系统是一种用于收集、存储和分析大规模分布式系统日志的系统。它可以帮助开发人员和系统管理员实时监控和调试系统，提高系统可靠性和可用性，同时也可以用于日志分析和故障排查。 二、简单设计思路 日志收集&#xff…...

编程日记 2024/12/13 5:24:38

DApp开发如何平衡性能与去中心化？

DApp的核心价值在于信任、透明和去中心化，但这些特点往往伴随着性能的瓶颈和高成本。在DApp开发中，如何在保证去中心化的前提下提升性能，成为开发者面临的重要挑战。如何实现性能与去中心化的平衡是一个重要课题。 一、为什么去中心化影响性…...

编程日记 2024/12/13 5:20:34

RK3588开发笔记-Buildroot编译Qt5WebEngine-5.15.10

目录 前言 一、Qt5WebEngine简介 二、Qt5WebEngine编译 总结 前言 Rockchip RK3588是一款强大的多核处理器，广泛应用于边缘计算、人工智能、嵌入式系统等领域。为了在RK3588上运行自定义的Linux系统，并使用Qt5WebEngine进行Web内容渲染，Buildroot是一个非常合适的工具。本…...

编程日记 2024/12/13 5:19:32

2024年12月GESPC++三级真题解析

一、单选题（每题2分，共30分） 题目123456789101112131415答案 B D A A D B C A A D D C D C A 1.下列二进制表示的十进制数值分别是（ ）[10000011]原（ ） [10000011]补&#xff…...

编程日记 2024/12/13 5:18:31

vue-router路由传参的两种方式（params 和 query ）

一、vue-router路由传参问题 1、概念： A、vue 路由传参的使用场景一般应用在父路由跳转到子路由时，携带参数跳转。 B、传参方式可划分为 params 传参和 query 传参； C、而 params 传参又可分为在 url 中显示参数和不显示参数两种方式&#x…...

编程日记 2024/12/13 5:17:30

Asp.net 做登录验证码（MVC）

public class ValidateCode{/// <summary>/// 创建随机数/// </summary>/// <param name"num"></param>/// <returns></returns>public string CreateRandom(int num){string str "ABCDEFGHJKMNPQRSTUVWXYZabcdefghjkmnpq…...

编程日记 2024/12/13 5:15:27

在 Chrome中直接调用大型语言模型的API

AI 时代的高速发展&#xff0c;我们都习惯了使用 ChatGPT、Claude、Gemini 和其他 AI 工具来询问各种问题&#xff0c;目前大部分的 AI 应用都是通过服务端 API 来实现的。 如果想要在 Web 上使用 AI 功能往往需要靠服务器来处理一些非常大的模型。这在制作一些生成内容的 AI …...

编程日记 2024/12/13 5:14:25

微信小程序调用腾讯地图-并解读API文档 JavaScript SDK和 WebService API

搜索&#xff1a;腾讯位置服务 找到API文档&#xff1a; 入门中第一步&#xff1a;申请开发者密钥key 前往控制台&#xff1a; 创建应用并获取key: 设置key的时候&#xff0c;还需要小程序的APPID。所以要前往微信公众平台中获取小程序的APPID&#xff1a; 限制要求&#xff1a…...

编程日记 2024/12/13 5:13:23

WPF 控件

<div id"content_views" class"htmledit_views"><p id"main-toc"><strong>目录</strong></p> WPF基础控件 按钮控件&#xff1a; Button:按钮 RepeatButton:长按按钮 RadioButton:单选按钮 数据显示控件 Te…...

编程日记 2024/12/13 5:11:17

VScode执行任务

背景 在vscode 中 如果执行命令需要传递进来参数&#xff0c;那么直接通过命令行终端的方式不太方便。通过task 任务的方式来进行启动执行&#xff0c;降低反复输入参数等繁琐工作。 首先可以查看vscode 官方文档 task 启动 crtl shift p .vscode/task.json 示例 执行cp…...

编程日记 2024/12/13 5:10:14

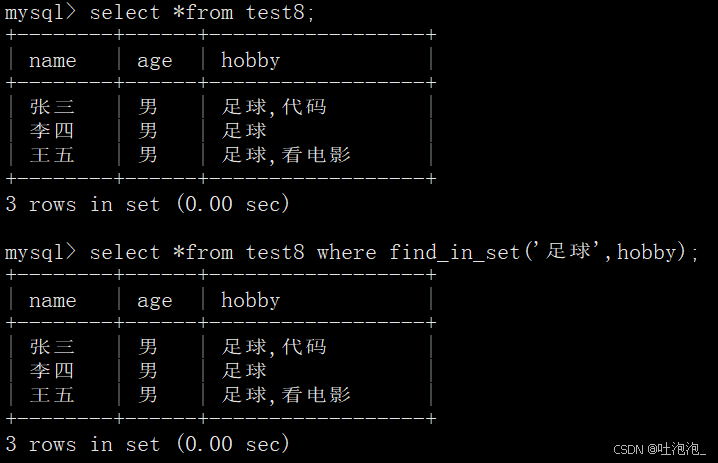
MySQL(数据类型)

目录 1. 数值类型 2. bit类型 3.小数类型 3. 字符串类型 4 日期和时间类型 5. enum和set 1. 数值类型 对标C语言&#xff1a; tinyint->char(1字节)&#xff1a; 有符号&#xff1a;127 ~ 255 无符号&#xff1a;0 ~ -128。 smalli…...

编程日记 2024/12/13 5:06:09

pytorch中的tqdm库

tqdm 是一个 Python 的进度条库&#xff0c;名字来源于阿拉伯语 "taqaddum"&#xff08;意思是“进步”&#xff09;。它以简单易用、高效著称&#xff0c;常用于循环操作中显示进度信息。 基本用法 1. 普通循环 tqdm 可以轻松为 for 循环添加进度条&#xff1a; …...

编程日记 2024/12/13 5:00:03

k8s从入门到放弃之Ingress七层负载

k8s从入门到放弃之Ingress七层负载 在Kubernetes&#xff08;简称K8s&#xff09;中&#xff0c;Ingress是一个API对象&#xff0c;它允许你定义如何从集群外部访问集群内部的服务。Ingress可以提供负载均衡、SSL终结和基于名称的虚拟主机等功能。通过Ingress&#xff0c;你可…...

编程新知 2025/9/7 0:12:53

【力扣数据库知识手册笔记】索引

索引 索引的优缺点 优点1. 通过创建唯一性索引&#xff0c;可以保证数据库表中每一行数据的唯一性。2. 可以加快数据的检索速度&#xff08;创建索引的主要原因&#xff09;。3. 可以加速表和表之间的连接&#xff0c;实现数据的参考完整性。4. 可以在查询过程中&#xff0c;…...

编程新知 2026/1/25 4:36:37

《从零掌握MIPI CSI-2: 协议精解与FPGA摄像头开发实战》-- CSI-2 协议详细解析 (一）

CSI-2 协议详细解析 (一&#xff09; 1. CSI-2层定义&#xff08;CSI-2 Layer Definitions&#xff09; 分层结构 &#xff1a;CSI-2协议分为6层&#xff1a; 物理层&#xff08;PHY Layer&#xff09; &#xff1a; 定义电气特性、时钟机制和传输介质&#xff08;导线&#…...

编程新知 2026/2/10 13:50:25

Python爬虫（二）：爬虫完整流程

爬虫完整流程详解&#xff08;7大核心步骤实战技巧&#xff09; 一、爬虫完整工作流程 以下是爬虫开发的完整流程&#xff0c;我将结合具体技术点和实战经验展开说明&#xff1a; 1. 目标分析与前期准备 网站技术分析&#xff1a; 使用浏览器开发者工具&#xff08;F12&…...

编程新知 2025/10/19 5:48:51

多种风格导航菜单 HTML 实现（附源码）

下面我将为您展示 6 种不同风格的导航菜单实现&#xff0c;每种都包含完整 HTML、CSS 和 JavaScript 代码。 1. 简约水平导航栏 <!DOCTYPE html> <html lang"zh-CN"> <head><meta charset"UTF-8"><meta name"viewport&qu…...

编程新知 2026/2/2 2:49:11

均衡后的SNRSINR

本文主要摘自参考文献中的前两篇&#xff0c;相关文献中经常会出现MIMO检测后的SINR不过一直没有找到相关数学推到过程&#xff0c;其中文献[1]中给出了相关原理在此仅做记录。 1. 系统模型 复信道模型 n t n_t nt​ 根发送天线&#xff0c; n r n_r nr​ 根接收天线的 MIMO 系…...

编程新知 2026/1/30 4:47:24

Selenium常用函数介绍

目录 一&#xff0c;元素定位 1.1 cssSeector 1.2 xpath 二&#xff0c;操作测试对象 三&#xff0c;窗口 3.1 案例 3.2 窗口切换 3.3 窗口大小 3.4 屏幕截图 3.5 关闭窗口 四&#xff0c;弹窗 五&#xff0c;等待 六&#xff0c;导航 七&#xff0c;文件上传 …...

编程新知 2026/1/29 3:55:23

uniapp 实现腾讯云IM群文件上传下载功能

UniApp 集成腾讯云IM实现群文件上传下载功能全攻略 一、功能背景与技术选型 在团队协作场景中&#xff0c;群文件共享是核心需求之一。本文将介绍如何基于腾讯云IMCOS&#xff0c;在uniapp中实现&#xff1a; 群内文件上传/下载文件元数据管理下载进度追踪跨平台文件预览 二…...

编程新知 2025/9/14 20:44:53

Xela矩阵三轴触觉传感器的工作原理解析与应用场景

Xela矩阵三轴触觉传感器通过先进技术模拟人类触觉感知&#xff0c;帮助设备实现精确的力测量与位移监测。其核心功能基于磁性三维力测量与空间位移测量&#xff0c;能够捕捉多维触觉信息。该传感器的设计不仅提升了触觉感知的精度&#xff0c;还为机器人、医疗设备和制造业的智…...

编程新知 2026/2/6 12:27:51

DeepSeek源码深度解析 × 华为仓颉语言编程精粹——从MoE架构到全场景开发生态

前言 在人工智能技术飞速发展的今天&#xff0c;深度学习与大模型技术已成为推动行业变革的核心驱动力&#xff0c;而高效、灵活的开发工具与编程语言则为技术创新提供了重要支撑。本书以两大前沿技术领域为核心&#xff0c;系统性地呈现了两部深度技术著作的精华&#xff1a;…...

编程新知 2026/2/5 4:33:51