论文学习——多种变化环境下基于多种群进化的动态约束多目标优化
论文题目:Multipopulation Evolution-Based Dynamic Constrained Multiobjective Optimization Under Diverse Changing Environments
多种变化环境下基于多种群进化的动态约束多目标优化(Qingda Chen , Member, IEEE, Jinliang Ding , Senior Member, IEEE, Gary G. Yen , Fellow, IEEE, Shengxiang Yang , Senior Member, IEEE, and Tianyou Chai , Life Fellow, IEEE)IEEE TRANSACTIONS ON EVOLUTIONARY COMPUTATION, VOL. 28, NO. 3, JUNE 2024
刚开始学习多目标优化算法,不作商业用途,如果有不正确的地方请指正!
个人总结:
2022年出的一篇文章和上次看的swarm的那边协同进化的分类有点像,
将种群划分为可行,不可行分为非支配不可行和支配不可行。
摘要
- 动态约束多目标优化涉及真实Pareto最优前沿分布的不规则变化,约束引起的可行域的剧烈变化,以及由于不同变化环境导致的最优距离变量的移动方向和大小。
- 提出了一种基于多种群进化的动态约束多目标优化算法。在该算法中,我们设计了一个部落分类算子,根据可行性检验和目标值将种群划分为不同的部落,这有利于驱动种群向可行域和帕累托最优前沿移动。
- 同时,提出一种种群选择策略,从部落中识别出有希望的解决方案,并利用它们来更新种群。距离变量的最优值随着动态环境的不同而变化,因此,我们为不同部落中的解设计了动态响应策略,以估计它们的距离以接近Pareto最优前沿,并重新生成有希望的解。
- 此外,设计了一个可扩展的生成器来模拟动态环境下真实世界问题中最优距离变量的不同运动方向和大小,得到一组改进的测试问题。
引言
距离变量的定义:帕累托最优解中的一个决策变量被认为是一个距离变量,如果改变x中的xi只能得到一个等于x、支配x或被x支配的决策向量(就是扰动以后只存在支配关系,收敛性决策变量)
动态约束多目标优化问题特征
1.时间变化下无约束PF和可行区域和真实PF都会发生变化
2.不可行解的数量随可行域波动,动态可行域的不规则边界使不可行解的评价值多样化。例如,图1 ( a )中的解E的约束违反度( CV )值大于图1 ( b )中的解E的CV值,但图1 ( a )中的解E更容易成为非支配解.
3.在动态环境下,DPOSs中距离变量的最优值在不同的方向和量级上移动,有的表现出剧烈的变化,有的则可能在较小的量级上移动,使得最优距离变量的移动方向和量级复杂化。

本文提出的想法
1。为了充分利用不同性能的解,特别是接近DPOF的解,本文提出了一种部落分类算子,将解按照其可行性和目标值划分到不同的部落中,驱使种群向真正的DPOF靠近。
2。本文设计了一种种群选择算子,根据支配算子从不可行部落中识别出的可行解和有希望的不可行解来更新种群,提高了种群的多样性和算法的寻优效率。
3。为了应对不同的变化环境,我们提出了一种动态响应策略来估计不同部落中向新的DPOF移动的距离变量的方向和大小,并根据评估值更新所有的解决方案,从而快速地更新靠近DPOF的初始化种群。
4。为了保证DCMOPs测试问题中的最优距离变量具有与现实问题一致的变化特性,我们设计了一个可扩展的生成器,在动态环境变化时,距离变量的最优值具有不同的移动方向和大小,测试了算法对DPOSs的跟踪能力。
背景及相关工作
A.DCMOP基础
B.约束处理技术
1.惩罚函数策略
2.分离目标和约束的方法
3.多目标制定
4.转化CMOPs的方法
5.混合方法
6.改变繁殖算子的方法
C.动态响应策略
提出框架与实施
A.mEDCMOA算法框架

B.初始化
算法初始化时,至少需要有一个可行解,否则就重新生成初始化种群。
C.部落分类算子
一些不可行解[如图1 ( a )中的解A , E和F]可能帮助目标值较大的可行解[例如,图1 ( a )中的解I]跟踪DPOFs,将其他不可行解[例如,图1 ( a )中的解J]推入可行域或靠近DPOFs。


提出了一种部落分类算子,根据可行性检验和目标值将种群划分为不同的部落。
首先根据可行性将种群划分为可行和不可行的(分别为FT和IT)部落,并利用非支配解选择算子从FT中更新AS
本文提出根据不可行解是否被非支配解支配将其划分到不同的部落中。,如果不可行解x的目标值不劣于非支配解的目标值,则称x为非支配不可行解;否则,x被认为是一个占优的不可行解。基于上述定义,将不可行解划分为支配和非支配不可行部落( DIT和NIT)。
D交配和种群选择算子
采用SBX和PM算子。
为了平衡算法的收敛速度和种群的多样性,本文提出了一种种群选择算子,在可行解数量不足的情况下,可以使用一些非支配和支配的不可行解来更新种群。
首先,清除若干部落(即FT、IT、DIT和NIT),并采用部落分类算子将P和Q中的解分类为FT、DIT和NIT。所有可行解都复制到一个空集NP上。
其次,如果非支配不可行解NIT 的数量大于N - | FT |,则将部分非支配不可行解NIT 推入NP,而不考虑支配不可行解。考虑到在靠近DPOFs [如图1 ( a )中的解F]的不可行解中的微小调整可能有助于它们成为可行解甚至非支配解,我们提出了一个支配算子来从NIT中选择N - | FT |非支配不可行解。具体来说,在具有最小目标函数的DCMOP中,NIT中具有大目标值的解更接近真实的DPOF。

E。动态响应策略
当环境发生变化时,通过修改不同部落中的先前解和随机解来重新生成初始种群。
首先,mEDCMOA通过初始化方法在变化的环境中随机产生N个解的一半,并重新计算之前解的目标值和CV值。所有解(即,随机的和先前的解决方案)由部落分类算子推送到不同的部落中。
其次,计算每个解的适应度值,确定每个部落中适应度值为0的解的 每个距离变量的调整方向和大小。
对于FT中适应度值为零的解,在该解的一个维度上增加一个正值δ。如果这个决策变量仍然在[ Lj , Uj],并且这个解的目标值中至少有一个被改进,那么δ被不断地添加到相应的维度中,直到这个个体不再被改进;否则,一维搜索策略按δ的值向该维度递减,δ在相应的维度上不断减小,直到该个体不再被改进。
计算出方向

修正
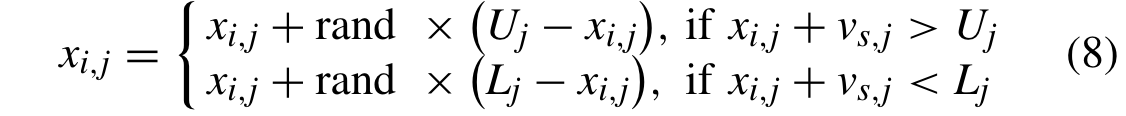
相关文章:
论文学习——多种变化环境下基于多种群进化的动态约束多目标优化
论文题目:Multipopulation Evolution-Based Dynamic Constrained Multiobjective Optimization Under Diverse Changing Environments 多种变化环境下基于多种群进化的动态约束多目标优化(Qingda Chen , Member, IEEE, Jinliang Ding , Senior Member, …...
Jenkins参数化构建详解(This project is parameterized)
本文详细介绍了Jenkins中不同类型的参数化构建方法,包括字符串、选项、多行文本、布尔值和git分支参数的配置,以及如何使用ActiveChoiceParameter实现动态获取参数选项。通过示例展示了传统方法和声明式pipeline的语法 文章目录 1. Jenkins的参数化构建1…...
Cerebras 推出 CePO,填补推理与规划能力的关键空白
每周跟踪AI热点新闻动向和震撼发展 想要探索生成式人工智能的前沿进展吗?订阅我们的简报,深入解析最新的技术突破、实际应用案例和未来的趋势。与全球数同行一同,从行业内部的深度分析和实用指南中受益。不要错过这个机会,成为AI领…...

广东省食品销售中高级题库及答案
1.有关食品安全标准的说法正确的是(C)。 A.鼓励性标准 B.推荐性标准 C.强制性标准 D.引导性标准 2.食品经营许可证载明的许可事项发生变化的,食品经营者应当在变化后(D)个工作日内向原发证的食品药品监督管理部门申请变更经营许可。 A.3 B.5 C.7 D.10 3.食品销售经营者对食品…...
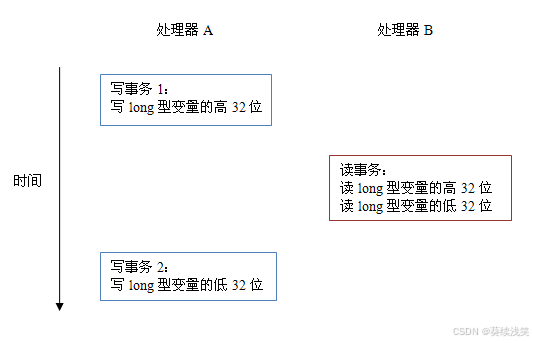
JAVA基础-深入理解Java内存模型(一)-- 重排序与先行发生原则(happens-before)
深入理解Java内存模型(一)-- 重排序 很棒的一个关于Java内存模型系列文章,首先感谢作者,转载自深入理解java内存模型系列文章 ,为了方便阅读,做了一些内容整合和重排版。 提纲 Java线程之间的通信对程序…...

【Lambda】java之lambda表达式stream流式编程操作集合
java之lambda表达式&stream流式编程操作集合 1 stream流概念1.1 中间操作1.1.1 无状态操作1.1.2 有状态操作 1.2 终端操作1.2.1 非短路操作1.2.2 短路操作 2 steam流的生成2.1 方式一:数组转为stream流2.2 方式二:集合转为steam流2.3 方式三…...
家具购物小程序+php
基于微信小程序的家具购物小程序的设计与实现 摘要 随着信息技术在管理上越来越深入而广泛的应用,管理信息系统的实施在技术上已逐步成熟。本文介绍了基于微信小程序的家具购物小程序的设计与实现的开发全过程。通过分析基于微信小程序的家具购物小程序的设计与实…...

【GIS教程】使用GDAL-Python将tif转为COG并在ArcGIS Js前端加载-附完整代码
目录 一、数据格式 二、COG特点 三、使用GDAL生成COG格式的数据 四、使用ArcGIS Maps SDK for JavaScript加载COG格式数据 一、数据格式 COG(Cloud optimized GeoTIFF)是一种GeoTiff格式的数据。托管在 HTTP 文件服务器上,可以代替geose…...
与cad交互)
VB.net进行CAD二次开发(二)与cad交互
开发过程遇到了一个问题:自制窗口与控件与CAD的交互。 启动类,调用非模式窗口 Imports Autodesk.AutoCAD.Runtime Public Class Class1 //CAD启动界面 <CommandMethod("US")> Public Sub UiStart() Dim myfrom As Form1 New…...

【NLP 11、Adam优化器】
祝你先于春天, 翻过此间铮铮山峦 —— 24.12.8 一、Adam优化器的基本概念 定义 Adam(Adaptive Moment Estimation)是一种基于梯度的优化算法,用于更新神经网络等机器学习模型中的参数。它结合了动量法(Momentum&…...
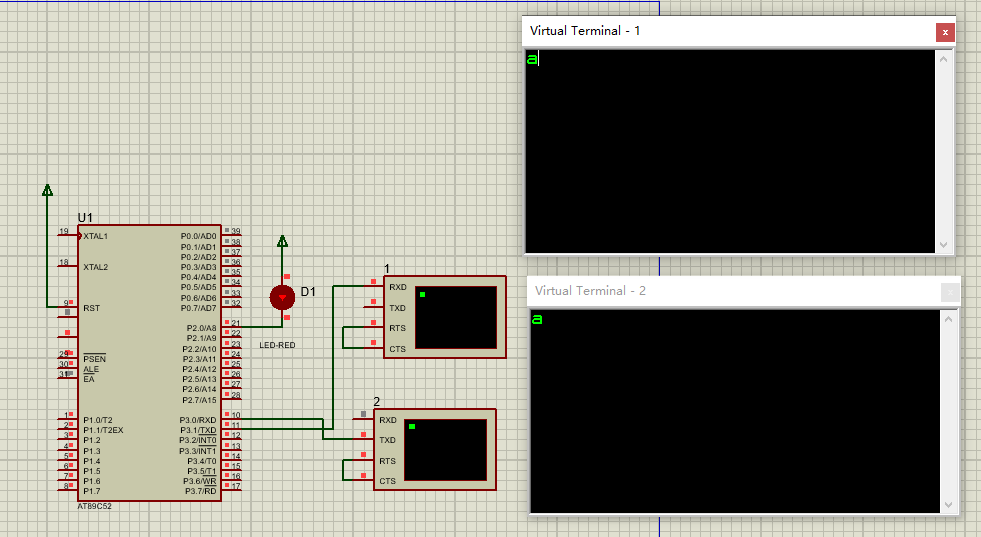
51单片机应用开发(进阶)---串口接收字符命令
实现目标 1、巩固UART知识; 2、掌握串口接收字符数据; 3、具体实现目标:(1)上位机串口助手发送多字符命令,单片机接收命令作相应的处理(如:openled1 即打开LED1;closeled1 即关…...

redis 怎么样删除list
在 Redis 中,可以使用以下方法删除列表或列表中的元素: 1. 删除整个列表 使用 DEL 命令删除一个列表键: DEL mylist这个命令会删除键 mylist 及其值(无论 mylist 是一个列表还是其他类型的键)。 2. 删除列表中的部分…...

【数据结构——内排序】快速排序(头歌实践教学平台习题)【合集】
目录😋 任务描述 测试说明 我的通关代码: 测试结果: 任务描述 本关任务:实现快速排序算法。 测试说明 平台会对你编写的代码进行测试: 测试输入示例: 10 6 8 7 9 0 1 3 2 4 5 (说明:第一行是元素个数&a…...
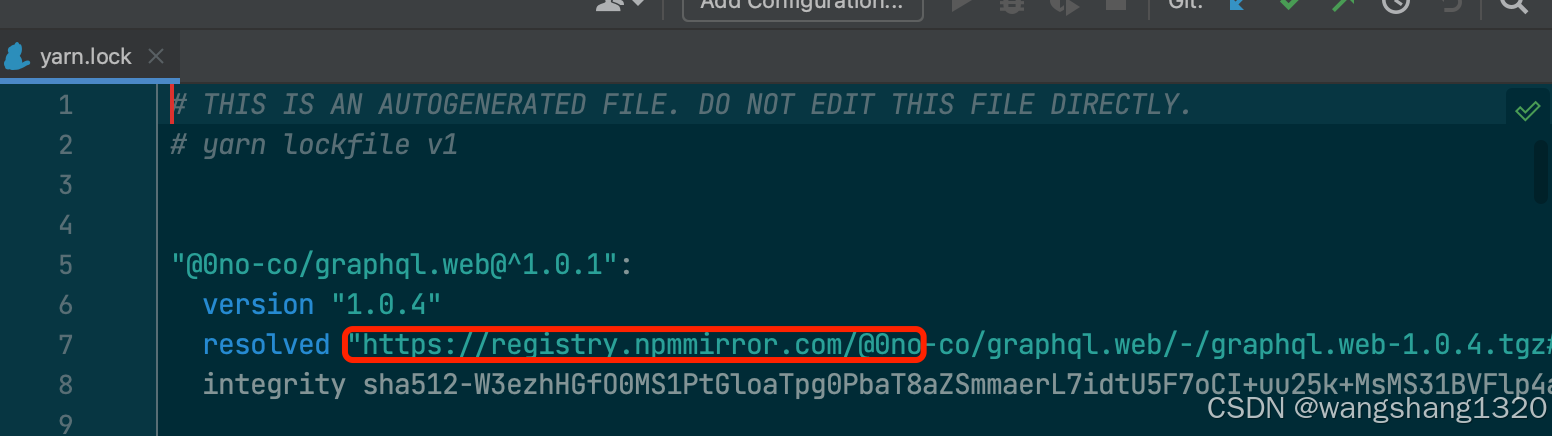
npm或yarn包配置地址源
三种方法 1.配置.npmrc 文件 在更目录新增.npmrc文件 然后写入需要访问的包的地址 2.直接yarn.lock文件里面修改地址 简单粗暴 3.yarn install 的时候添加参数 设置包的仓库地址 yarn config set registry https://registry.yarnpkg.com 安装:yarn install 注意…...

STUN服务器用于内网NAT的方案
在内网中部署 STUN 服务器的场景通常用于处理多层 NAT 或内网客户端之间的通信需求,尤其是在大企业或学校等复杂网络环境下。通过 STUN 服务器,可以帮助客户端设备检测和适配 NAT 转换规则,进而支持 WebRTC 或其他实时通信技术的正常运行。 …...
Linux 简单命令总结
1. 简单命令 1.1. ls 列出该目录下的所有子目录与文件,后面还可以跟上一些选项 常用选项: ・-a 列出目录下的所有文件,包括以。开头的隐含文件。 ・-d 将目录象文件一样显示,而不是显示其下的文件。如:ls -d 指定目…...

Vue.js组件开发:提升你的前端工程能力
Vue.js 是一个用于构建用户界面的渐进式框架,它允许开发者通过组件化的方式创建可复用且易于管理的代码。在 Vue.js 中开发组件是一个直观且高效的过程,下面我将概述如何创建和使用 Vue 组件,并提供一些最佳实践。 1. 创建基本组件 首先&am…...

使用 Pandas 读取 JSON 数据的五种常见结构解析
文章目录 引言JSON 数据的五种常见结构1. split 结构2. records 结构3. index 结构4. columns 结构5. values 结构 引言 在日常生活中,我们经常与各种数据打交道,无论是从网上购物的订单信息到社交媒体上的动态更新。JSON(JavaScript Object…...

C++鼠标轨迹算法(鼠标轨迹模拟真人移动)
一.简介 鼠标轨迹算法是一种模拟人类鼠标操作的程序,它能够模拟出自然而真实的鼠标移动路径。 鼠标轨迹算法的底层实现采用C/C语言,原因在于C/C提供了高性能的执行能力和直接访问操作系统底层资源的能力。 鼠标轨迹算法具有以下优势: 模拟…...
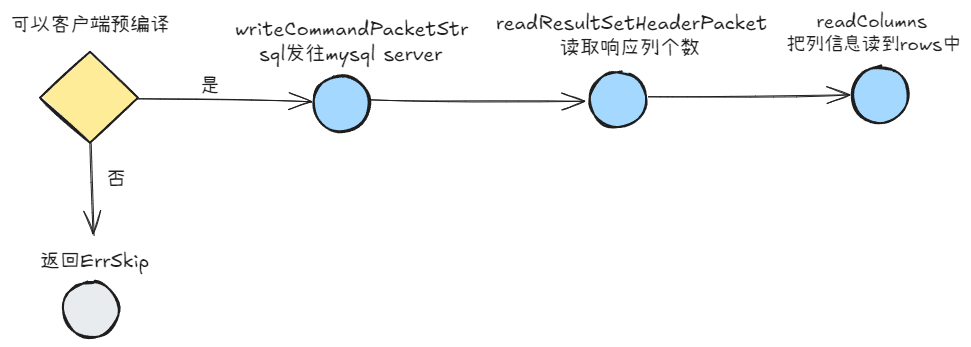
Go mysql驱动源码分析
文章目录 前言注册驱动连接器创建连接交互协议读写数据读数据写数据 mysqlConncontext超时控制 查询发送查询请求读取查询响应 Exec发送exec请求读取响应 预编译客户端预编译服务端预编译生成prepareStmt执行查询操作执行Exec操作 事务读取响应query响应exec响应 总结 前言 go…...

KubeSphere 容器平台高可用:环境搭建与可视化操作指南
Linux_k8s篇 欢迎来到Linux的世界,看笔记好好学多敲多打,每个人都是大神! 题目:KubeSphere 容器平台高可用:环境搭建与可视化操作指南 版本号: 1.0,0 作者: 老王要学习 日期: 2025.06.05 适用环境: Ubuntu22 文档说…...

设计模式和设计原则回顾
设计模式和设计原则回顾 23种设计模式是设计原则的完美体现,设计原则设计原则是设计模式的理论基石, 设计模式 在经典的设计模式分类中(如《设计模式:可复用面向对象软件的基础》一书中),总共有23种设计模式,分为三大类: 一、创建型模式(5种) 1. 单例模式(Sing…...

【Oracle APEX开发小技巧12】
有如下需求: 有一个问题反馈页面,要实现在apex页面展示能直观看到反馈时间超过7天未处理的数据,方便管理员及时处理反馈。 我的方法:直接将逻辑写在SQL中,这样可以直接在页面展示 完整代码: SELECTSF.FE…...

Vue3 + Element Plus + TypeScript中el-transfer穿梭框组件使用详解及示例
使用详解 Element Plus 的 el-transfer 组件是一个强大的穿梭框组件,常用于在两个集合之间进行数据转移,如权限分配、数据选择等场景。下面我将详细介绍其用法并提供一个完整示例。 核心特性与用法 基本属性 v-model:绑定右侧列表的值&…...

Spring是如何解决Bean的循环依赖:三级缓存机制
1、什么是 Bean 的循环依赖 在 Spring框架中,Bean 的循环依赖是指多个 Bean 之间互相持有对方引用,形成闭环依赖关系的现象。 多个 Bean 的依赖关系构成环形链路,例如: 双向依赖:Bean A 依赖 Bean B,同时 Bean B 也依赖 Bean A(A↔B)。链条循环: Bean A → Bean…...

《C++ 模板》
目录 函数模板 类模板 非类型模板参数 模板特化 函数模板特化 类模板的特化 模板,就像一个模具,里面可以将不同类型的材料做成一个形状,其分为函数模板和类模板。 函数模板 函数模板可以简化函数重载的代码。格式:templa…...

MFC 抛体运动模拟:常见问题解决与界面美化
在 MFC 中开发抛体运动模拟程序时,我们常遇到 轨迹残留、无效刷新、视觉单调、物理逻辑瑕疵 等问题。本文将针对这些痛点,详细解析原因并提供解决方案,同时兼顾界面美化,让模拟效果更专业、更高效。 问题一:历史轨迹与小球残影残留 现象 小球运动后,历史位置的 “残影”…...

R 语言科研绘图第 55 期 --- 网络图-聚类
在发表科研论文的过程中,科研绘图是必不可少的,一张好看的图形会是文章很大的加分项。 为了便于使用,本系列文章介绍的所有绘图都已收录到了 sciRplot 项目中,获取方式: R 语言科研绘图模板 --- sciRplothttps://mp.…...

深度学习之模型压缩三驾马车:模型剪枝、模型量化、知识蒸馏
一、引言 在深度学习中,我们训练出的神经网络往往非常庞大(比如像 ResNet、YOLOv8、Vision Transformer),虽然精度很高,但“太重”了,运行起来很慢,占用内存大,不适合部署到手机、摄…...

从零开始了解数据采集(二十八)——制造业数字孪生
近年来,我国的工业领域正经历一场前所未有的数字化变革,从“双碳目标”到工业互联网平台的推广,国家政策和市场需求共同推动了制造业的升级。在这场变革中,数字孪生技术成为备受关注的关键工具,它不仅让企业“看见”设…...
