数值分析——插值法(二)
文章目录
- 前言
- 一、Hermite插值
- 1.两点三次Hermite插值
- 2.两点三次Hermite插值的推广
- 3.非标准型Hermite插值
- 二、三次样条插值
- 1.概念
- 2.三弯矩方程
前言
之前写过Lagrange插值与Newton插值法的内容,这里介绍一些其他的插值方法,顺便复习数值分析.
一、Hermite插值
实际应用中,为了使插值函数更好地切合原函数,不仅要求节点的函数值相等,还要求导数值相同,甚至高阶导数也相等,这类插值问题称为Hermite插值
1.两点三次Hermite插值
给定y=f(x)在节点x0,x1上的函数值和导数值:
y j = f ( x j ) , m j = f ′ ( x j ) , j = 0 , 1. y_j=f(x_j),m_j=f'(x_j),j=0,1. yj=f(xj),mj=f′(xj),j=0,1.
求多项式 H 3 ( x ) H_3(x) H3(x)满足插值条件
H 3 ( x j ) = y j , H 3 ′ ( x j ) = m j , j = 0 , 1. H_3(x_j)=y_j,H'_3(x_j)=m_j,j=0,1. H3(xj)=yj,H3′(xj)=mj,j=0,1.
类似Lagrange插值多项式,我们可以设
H 3 ( x ) = y 0 α 0 ( x ) + y 1 α 1 ( x ) + m 0 β 0 ( x ) + m 1 β 1 ( x ) H_3(x)=y_0\alpha_0(x)+y_1\alpha_1(x)+m_0\beta_0(x)+m_1\beta_1(x) H3(x)=y0α0(x)+y1α1(x)+m0β0(x)+m1β1(x)
为三次Hermite插值多项式,其中 α 0 ( x ) , α 1 ( x ) , β 0 ( x ) , β 1 ( x ) \alpha_0(x),\alpha_1(x),\beta_0(x),\beta_1(x) α0(x),α1(x),β0(x),β1(x)称为Hermite插值基函数.
基函数满足如下条件:
α j ( x j ) = δ j i , α j ′ ( x i ) = 0 , β j ( x i ) = 0 , β j ′ ( x i ) = δ j i , i , j = 0 , 1 \alpha_j(x_j)=\delta_{ji},\alpha'_j(x_i)=0,\\\beta_j(x_i)=0,\beta'_j(x_i)=\delta_{ji},\\ i,j=0,1 αj(xj)=δji,αj′(xi)=0,βj(xi)=0,βj′(xi)=δji,i,j=0,1
其中 δ j i = { 1 j = i 0 j ≠ i \delta_{ji}=\begin{cases}1&j=i\\ 0&j\neq i \end{cases} δji={10j=ij=i
我们可以找到唯一的三次Hermite插值多项式(推导略),即
H 3 ( x ) = y 0 [ 1 + 2 l 1 ( x ) ] l 0 2 ( x ) + y 1 [ 1 + 2 l 0 ( x ) ] l 1 2 ( x ) + m 0 ( x − x 0 ) l 0 2 ( x ) + m 1 ( x − x 1 ) l 1 2 ( x ) H_3(x)=y_0[1+2l_1(x)]l^2_0(x)+y_1[1+2l_0(x)]l^2_1(x)\\+m_0(x-x_0)l^2_0(x)+m_1(x-x_1)l^2_1(x) H3(x)=y0[1+2l1(x)]l02(x)+y1[1+2l0(x)]l12(x)+m0(x−x0)l02(x)+m1(x−x1)l12(x)
这里的 l i l_i li为Lagrange插值基函数, l 0 ( x ) = x − x 1 x 0 − x 1 , l 1 ( x ) = x − x 0 x 1 − x 0 l_0(x)=\frac{x-x_1}{x_0-x_1},l_1(x)=\frac{x-x_0}{x_1-x_0} l0(x)=x0−x1x−x1,l1(x)=x1−x0x−x0
2.两点三次Hermite插值的推广
设 x i ∈ [ a , b ] ( i = 0 , 1 , ⋯ , n ) x_i\in[a,b](i=0,1,\cdots,n) xi∈[a,b](i=0,1,⋯,n)为n+1个互异节点,给定 y = f ( x ) y=f(x) y=f(x)在节点上的函数值和导数值: y j = f ( x j ) , m j = f ′ ( x j ) , j = 0 , ⋯ , n . y_j=f(x_j),m_j=f'(x_j),j=0,\cdots,n. yj=f(xj),mj=f′(xj),j=0,⋯,n.要求插值多项式 H 2 n + 1 ( x ) H_{2n+1}(x) H2n+1(x)满足插值条件
H 2 n + 1 ( x j ) = y j , H 2 n + 1 ′ ( x j ) = m j , j = 0 , ⋯ , n . H_{2n+1}(x_j)=y_j,H'_{2n+1}(x_j)=m_j,j=0,\cdots,n. H2n+1(xj)=yj,H2n+1′(xj)=mj,j=0,⋯,n.有n+1个函数值和n+1个导数值共2n+2个条件,可确定满足插值条件次数不超过2n+1次的多项式 H 2 n + 1 ( x ) H_{2n+1}(x) H2n+1(x).
公式:
H 2 n + 1 = ∑ j = 0 n { f ( x j ) [ 1 − 2 ( x − x j ) l j ′ ( x j ) ] l j 2 ( x ) + f ′ ( x j ) ( x − x j ) l j 2 ( x ) } H_{2n+1}=\sum_{j=0}^n \{f(x_j)[1-2(x-x_j)l'_j(x_j)]l^2_j(x)+f'(x_j)(x-x_j)l^2_j(x)\} H2n+1=j=0∑n{f(xj)[1−2(x−xj)lj′(xj)]lj2(x)+f′(xj)(x−xj)lj2(x)}
其中 l j ( x ) = ( x − x 0 ) ⋯ ( x − x j − 1 ) ( x − x j + 1 ) ⋯ ( x − x n ) ( x j − x 0 ) ⋯ ( x j − x j − 1 ) ( x j − x j + 1 ) ⋯ ( x j − x n ) l_j(x)=\frac{(x-x_0)\cdots(x-x_{j-1})(x-x_{j+1})\cdots(x-x_n)}{(x_j-x_0)\cdots(x_j-x_{j-1})(x_j-x_{j+1})\cdots(x_j-x_n)} lj(x)=(xj−x0)⋯(xj−xj−1)(xj−xj+1)⋯(xj−xn)(x−x0)⋯(x−xj−1)(x−xj+1)⋯(x−xn)
3.非标准型Hermite插值
给出的函数值和导数值不等的情况,例题:

二、三次样条插值
Hermite只保证函数连续或其一阶导数连续,满足不了二阶导数连续的问题. 针对这一问题,产生了样条插值.
1.概念
给定区间[a,b]一个划分:
a = x 0 < x 1 ⋯ < x n − 1 < x n = b a=x_0<x_1\cdots <x_{n-1}<x_n=b a=x0<x1⋯<xn−1<xn=b
若函数S(x)满足
- 在每个小区间 [ x i , x i + 1 ] [x_i,x_{i+1}] [xi,xi+1]是分段三次多项式
- 具有二阶连续导数,即 S ( x ) ∈ C 2 [ a , b ] S(x)\in C^2[a,b] S(x)∈C2[a,b]
- 还满足插值条件: S ( x i ) = f ( x i ) = y i , i = 0 , 1 , 2 , ⋯ , n S(x_i)=f(x_i)=y_i,i=0,1,2,\cdots,n S(xi)=f(xi)=yi,i=0,1,2,⋯,n
则称S(x)为f(x)在[a,b]上的三次样条插值函数,
S ( x ) = { s 0 ( x ) , x ∈ [ x 0 , x 1 ] , s 1 ( x ) , x ∈ [ x 1 , x 2 ] , ⋮ s n − 1 ( x ) , x ∈ [ x n − 1 , x n ] , S(x)=\begin{cases}s_0(x),&x\in [x_0,x_1],\\ s_1(x),&x\in [x_1,x_2],\\ \vdots\\s_{n-1}(x),&x\in [x_{n-1},x_n],\end{cases} S(x)=⎩ ⎨ ⎧s0(x),s1(x),⋮sn−1(x),x∈[x0,x1],x∈[x1,x2],x∈[xn−1,xn],
其中, s i ( x ) s_i(x) si(x)为 [ x i , x i + 1 ] ( i = 0 , 1 , 2 , ⋯ , n − 1 ) [x_i,x_{i+1}](i=0,1,2,\cdots,n-1) [xi,xi+1](i=0,1,2,⋯,n−1)上的三次多项式,设
s i ( x ) = a i x 3 + b i x 2 + c i x + d i ( i = 0 , 1 , ⋯ , n − 1 ) , s_i(x)=a_ix^3+b_ix^2+c_ix+d_i(i=0,1,\cdots,n-1), si(x)=aix3+bix2+cix+di(i=0,1,⋯,n−1),
且满足 s i ( x i ) = y i , s i + 1 ( x i + 1 ) s_i(x_i)=y_i,s_{i+1}(x_{i+1}) si(xi)=yi,si+1(xi+1). 由三次样条函数的定义可知, S ( x ) S(x) S(x)满足下列条件:
{ S ( x i − 0 ) = S ( x i + 0 ) ( i = 1 , 2 , ⋯ , n − 1 ) , S ′ ( x i − 0 ) = S ′ ( x i + 0 ) ( i = 1 , 2 , ⋯ , n − 1 ) , S ′ ′ ( x i − 0 ) = S ′ ′ ( x i + 0 ) ( i = 1 , 2 , ⋯ , n − 1 ) , S ( x i ) = y i ( i = 0 , 1 , 2 , ⋯ , n ) \begin{cases}S(x_i-0)=S(x_i+0)&(i=1,2,\cdots,n-1),\\ S'(x_i-0)=S'(x_i+0)&(i=1,2,\cdots,n-1),\\ S''(x_i-0)=S''(x_i+0)&(i=1,2,\cdots,n-1),\\ S(x_i)=y_i&(i=0,1,2,\cdots,n) \end{cases} ⎩ ⎨ ⎧S(xi−0)=S(xi+0)S′(xi−0)=S′(xi+0)S′′(xi−0)=S′′(xi+0)S(xi)=yi(i=1,2,⋯,n−1),(i=1,2,⋯,n−1),(i=1,2,⋯,n−1),(i=0,1,2,⋯,n)
每个 s i ( x ) s_i(x) si(x)有4个待定系数,所以S(x)共有4n个待定系数,故需4n个方程才能确定. 前面已经得到2n+2(n-1)=4n-2个方程,还缺2个方程. 实际问题通常对样条函数在两个端点处的状态有要求,即所谓的边界条件. 常用的边界条件如下:
第一类边界条件:给定函数在端点处的一阶导数,即
S ′ ( x 0 ) = f 0 ′ , S ′ ( x n ) = f n ′ S'(x_0)=f_0',S'(x_n)=f'_n S′(x0)=f0′,S′(xn)=fn′
第二类边界条件:给定函数在端点处的二阶导数,即
S ′ ′ ( x 0 ) = f 0 ′ ′ , S ′ ′ ( x n ) = f n ′ ′ S''(x_0)=f''_0,S''(x_n)=f_n'' S′′(x0)=f0′′,S′′(xn)=fn′′
第三类边界条件:设 f ( x ) f(x) f(x)是周期函数,并设 x n − x 0 x_n-x_0 xn−x0是一个周期,于是要求 S ( x ) S(x) S(x)满足
S ′ ( x 0 ) = S ′ ( x n ) , S ′ ′ ( x 0 ) = S ′ ′ ( x n ) S'(x_0)=S'(x_n),S''(x_0)=S''(x_n) S′(x0)=S′(xn),S′′(x0)=S′′(xn)
2.三弯矩方程
设 S ′ ′ ( x j ) = M j , j = 0 , 1 , 2 , ⋯ , n S''(x_j)=M_j,j=0,1,2,\cdots,n S′′(xj)=Mj,j=0,1,2,⋯,n,下面计算 S ( x ) S(x) S(x)在 [ x j , x j + 1 ] [x_j,x_{j+1}] [xj,xj+1]的表达式 s j ( x ) s_j(x) sj(x).由于 s j ( x ) s_j(x) sj(x)是三次多项式,故 s j ′ ′ ( x ) s''_j(x) sj′′(x)为线性函数,且 s j ′ ′ ( x j ) = M j , s j ′ ′ ( x j + 1 ) = M j + 1 s_j''(x_j)=M_j,s''_j(x_{j+1})=M_{j+1} sj′′(xj)=Mj,sj′′(xj+1)=Mj+1.由线性插值公式可得
s j ′ ′ ( x ) = x j + 1 − x h j M j + x − x j h j M j + 1 s''_j(x)=\frac{x_{j+1}-x}{h_j}M_j+\frac{x-x_j}{h_j}M_{j+1} sj′′(x)=hjxj+1−xMj+hjx−xjMj+1
其中 h j = x j + 1 − x j h_j=x_{j+1}-x_j hj=xj+1−xj,求积分,可得
s j ( x ) = ( x j + 1 − x ) 3 6 h j M j + ( x − x j ) 3 6 h j M j + 1 + c 1 x + c 2 s_j(x)=\frac{(x_{j+1}-x)^3}{6h_j}M_j+\frac{(x-x_j)^3}{6h_j}M_{j+1}+c_1x+c_2 sj(x)=6hj(xj+1−x)3Mj+6hj(x−xj)3Mj+1+c1x+c2
将插值条件 s j ( x j ) = y j , s j ( x j + 1 ) = y i + 1 s_j(x_j)=y_j,s_j(x_{j+1})=y_{i+1} sj(xj)=yj,sj(xj+1)=yi+1代入,即课确定积分常数 c 1 c_1 c1和 c 2 c_2 c2. 整理后可得 s j ( x ) s_j(x) sj(x)的表达式为 s j ( x ) = ( x j + 1 − x ) 2 6 h j M j + ( x − x j ) 3 6 h j M j + 1 + ( y j − M j h j 2 6 ) x j + 1 − x h j + ( y i + 1 − M j + 1 h j 2 6 ) x − x j h j , j = 0 , 1 , ⋯ , n − 1 s_j(x)=\frac{(x_{j+1}-x)^2}{6h_j}M_j+\frac{(x-x_j)^3}{6h_j}M_{j+1}\\ +\left(y_j-\frac{M_jh_j^2}{6}\right)\frac{x_{j+1}-x}{h_j}+\left(y_{i+1}-\frac{M_{j+1}h_j^2}{6}\right)\frac{x-x_j}{h_j},j=0,1,\cdots,n-1 sj(x)=6hj(xj+1−x)2Mj+6hj(x−xj)3Mj+1+(yj−6Mjhj2)hjxj+1−x+(yi+1−6Mj+1hj2)hjx−xj,j=0,1,⋯,n−1
只需确定 M 0 , M 1 , ⋯ , M n M_0,M_1,\cdots,M_n M0,M1,⋯,Mn的值,即可给出 s j ( x ) s_j(x) sj(x)的表达式,从而可以得到 S ( x ) S(x) S(x)的表达式
s j ′ ( x ) = − ( x j + 1 − x ) 2 2 h j M j + ( x − x j ) 2 2 h j M j + 1 + y j + 1 − y j h j − h j 6 ( M j + 1 − M j ) s'_j(x)=-\frac{(x_{j+1}-x)^2}{2h_j}M_j+\frac{(x-x_j)^2}{2h_j}M_{j+1}+\frac{y_{j+1}-y_j}{h_j}-\frac{h_j}{6}(M_{j+1}-M_j) sj′(x)=−2hj(xj+1−x)2Mj+2hj(x−xj)2Mj+1+hjyj+1−yj−6hj(Mj+1−Mj)
根据条件 s j − 1 ′ ( x j − 0 ) = s j ′ ( x j + 0 ) s_{j-1}'(x_j-0)=s_j'(x_j+0) sj−1′(xj−0)=sj′(xj+0)可知
h j − 1 6 M j − 1 + h j − 1 + h j 3 M j + h j 6 M j + 1 = y j + 1 − y j h j − y j − y j − 1 h j − 1 , h j − 1 h j − 1 + h j M j − 1 + 2 M j + h j h j − 1 + h j M j + 1 = 6 f [ x j , x j + 1 ] − f [ x j − 1 , x j ] h j − 1 + h j , \frac{h_{j-1}}{6}M_{j-1}+\frac{h_{j-1}+h_j}{3}M_j+\frac{h_j}{6}M_{j+1}=\frac{y_{j+1}-y_j}{h_j}-\frac{y_j-y_{j-1}}{h_{j-1}},\\ \frac{h_{j-1}}{h_{j-1}+h_j}M_{j-1}+2M_j+\frac{h_j}{h_{j-1}+h_j}M_{j+1}=6\frac{f[x_j,x_{j+1}]-f[x_{j-1},x_j]}{h_{j-1}+h_j}, 6hj−1Mj−1+3hj−1+hjMj+6hjMj+1=hjyj+1−yj−hj−1yj−yj−1,hj−1+hjhj−1Mj−1+2Mj+hj−1+hjhjMj+1=6hj−1+hjf[xj,xj+1]−f[xj−1,xj],
整理后得到关于 M j − 1 , M j , M j + 1 M_{j-1},M_j,M_{j+1} Mj−1,Mj,Mj+1的方程:
μ j M j − 1 + 2 M j + λ j M j + 1 = d j , \mu_jM_{j-1}+2M_j+\lambda_jM_{j+1}=d_j, μjMj−1+2Mj+λjMj+1=dj,
其中 μ j = h j − 1 h j − 1 + h j , λ j = h j h j − 1 + h j d j = 6 f [ x j − 1 , x j , x j + 1 ] , μ j + λ j = 1 j = 1 , 2 , ⋯ , n − 1 \mu_j=\frac{h_{j-1}}{h_{j-1}+h_j},\lambda_j=\frac{h_j}{h_{j-1}+h_j}\\ d_j=6f[x_{j-1},x_j,x_{j+1}],\mu_j+\lambda_j=1\\ j=1,2,\cdots,n-1 μj=hj−1+hjhj−1,λj=hj−1+hjhjdj=6f[xj−1,xj,xj+1],μj+λj=1j=1,2,⋯,n−1
这里一共有n-1个方程,补充两个方程后可确定 M 0 , M 1 , ⋯ , M n M_0,M_1,\cdots,M_n M0,M1,⋯,Mn共n-1个未知量.
- 第一类边界条件: S ′ ( x 0 ) = f 0 ′ , S ′ ( x n ) = f n ′ S'(x_0)=f'_0,S'(x_n)=f_n' S′(x0)=f0′,S′(xn)=fn′
直接代入 s j ( x ) s_j(x) sj(x)的一阶导数表达式即得
2 M 0 + M 1 = 6 ( ( y 1 − y 0 ) / h 0 − f 0 ′ ) / h 0 ≡ d 0 , M n − 1 + 2 M n = 6 ( f n ′ − ( y n − y n − 1 ) / h n − 1 ) / h n − 1 ≡ d n . 2M_0+M_1=6((y_1-y_0)/h_0-f_0')/h_0\equiv d_0,\\ M_{n-1}+2M_n=6(f'_n-(y_n-y_{n-1})/h_{n-1})/h_{n-1}\equiv d_n. 2M0+M1=6((y1−y0)/h0−f0′)/h0≡d0,Mn−1+2Mn=6(fn′−(yn−yn−1)/hn−1)/hn−1≡dn.
与上面n-1个方程组联立可得n+1阶线性方程组
[ 2 1 μ 1 2 λ 1 μ 2 2 λ 2 ⋱ ⋱ ⋱ μ n − 1 2 λ n − 1 1 2 ] [ M 0 M 1 M 2 ⋮ M n − 1 M n ] = [ d 0 d 1 d 2 ⋮ d n − 1 d n ] \begin{bmatrix}2&1&&&&&\\ \mu_1&2&\lambda_1\\ &\mu_2&2&\lambda_2\\ &&\ddots&\ddots&\ddots\\ &&&\mu_{n-1}&2&\lambda_{n-1}\\ &&&&1&2\end{bmatrix}\begin{bmatrix}M_0\\M_1\\M_2\\ \vdots \\M_{n-1}\\M_n\end{bmatrix}=\begin{bmatrix}d_0\\d_1\\d_2\\ \vdots \\d_{n-1}\\d_n\end{bmatrix} 2μ112μ2λ12⋱λ2⋱μn−1⋱21λn−12 M0M1M2⋮Mn−1Mn = d0d1d2⋮dn−1dn
此方程组的系数矩阵严格对角占优,因此为非奇异矩阵,方程存在唯一解.可用追赶法求出三弯矩方程的解 M j . M_j. Mj. - 第二类边界条件: M 0 = f 0 ′ ′ , M n = f n ′ ′ M_0=f''_0,M_n=f_n'' M0=f0′′,Mn=fn′′
此时只需解n-1阶线性方程组
[ 2 λ 1 μ 2 2 λ 2 ⋱ ⋱ ⋱ μ n − 2 2 λ n − 2 μ n − 1 2 ] [ M 1 M 2 ⋮ M n − 1 M n ] = [ d 1 − μ 1 f 0 ′ ′ d 2 ⋮ d n − 2 d n − 1 − λ n − 1 f n ′ ′ ] \begin{bmatrix}2&\lambda_1&&&\\ \mu_2&2&\lambda_2\\ &\ddots&\ddots&\ddots\\ &&\mu_{n-2}&2&\lambda_{n-2}\\ &&&\mu_{n-1}&2\end{bmatrix}\begin{bmatrix}M_1\\M_2\\ \vdots \\M_{n-1}\\M_n\end{bmatrix}=\begin{bmatrix}d_1-\mu_1f''_0\\d_2\\ \vdots \\d_{n-2}\\d_{n-1}-\lambda_{n-1}f''_n\end{bmatrix} 2μ2λ12⋱λ2⋱μn−2⋱2μn−1λn−22 M1M2⋮Mn−1Mn = d1−μ1f0′′d2⋮dn−2dn−1−λn−1fn′′
此方程严格对角占优,存在唯一解. - 第三类边界条件: S ′ ( x 0 ) = S ′ ( x n ) , S ′ ′ ( x 0 ) = S ′ ′ ( x n ) S'(x_0)=S'(x_n),S''(x_0)=S''(x_n) S′(x0)=S′(xn),S′′(x0)=S′′(xn)
由此边界条件可得 M 0 = M n , λ n M 1 + μ n M n − 1 + 2 M n = d n , M_0=M_n,\\ \lambda_nM_1+\mu_nM_{n-1}+2M_n=d_n, M0=Mn,λnM1+μnMn−1+2Mn=dn,
其中 λ n = h 0 / ( h 0 + h n − 1 ) , μ n = h n − 1 / ( h 0 + h n − 1 ) , d n = 6 [ ( y 1 − y 0 ) / h 0 − ( y n − y n − 1 ) / h n − 1 ] / ( h 0 + h n − 1 ) . \lambda_n=h_0/(h_0+h_{n-1}),\mu_n=h_{n-1}/(h_0+h_{n-1}),\\ d_n=6[(y_1-y_0)/h_0-(y_n-y_{n-1})/h_{n-1}]/(h_0+h_{n-1}). λn=h0/(h0+hn−1),μn=hn−1/(h0+hn−1),dn=6[(y1−y0)/h0−(yn−yn−1)/hn−1]/(h0+hn−1).
与前面n-1个方程联立可得n阶线性方程组:
[ 2 λ 1 μ 2 2 λ 2 ⋱ ⋱ ⋱ μ n − 2 2 λ n − 2 λ n μ 2 2 ] [ M 1 M 2 ⋮ M n − 1 M n ] = [ d 0 d 1 d 2 ⋮ d n − 1 d n ] \begin{bmatrix}2&\lambda_1&&&\\ \mu_2&2&\lambda_2\\ &\ddots&\ddots&\ddots\\ &&\mu_{n-2}&2&\lambda_{n-2}\\ \lambda_n&&&\mu_2&2\end{bmatrix}\begin{bmatrix}M_1\\M_2\\ \vdots \\M_{n-1}\\M_n\end{bmatrix}=\begin{bmatrix}d_0\\d_1\\d_2\\ \vdots \\d_{n-1}\\d_n\end{bmatrix} 2μ2λnλ12⋱λ2⋱μn−2⋱2μ2λn−22 M1M2⋮Mn−1Mn = d0d1d2⋮dn−1dn
此方程组系数矩阵严格对角占优,存在唯一解.
参考书目:《数值分析》张雪莹
相关文章:

数值分析——插值法(二)
文章目录 前言一、Hermite插值1.两点三次Hermite插值2.两点三次Hermite插值的推广3.非标准型Hermite插值 二、三次样条插值1.概念2.三弯矩方程 前言 之前写过Lagrange插值与Newton插值法的内容,这里介绍一些其他的插值方法,顺便复习数值分析. 一、Hermi…...
杨振宁大学物理视频中黄色的字,c#写程序去掉
先看一下效果:(还有改进的余地) 写了个程序消除杨振宁大学物理中黄色的字 我的方法是笨方法,也比较刻板。 1,首先想到,把屏幕打印下来。c#提供了这样一个函数: Bitmap bmp new Bitmap(640, 48…...

uni-app 设置缓存过期时间【跨端开发系列】
🔗 uniapp 跨端开发系列文章:🎀🎀🎀 uni-app 组成和跨端原理 【跨端开发系列】 uni-app 各端差异注意事项 【跨端开发系列】uni-app 离线本地存储方案 【跨端开发系列】uni-app UI库、框架、组件选型指南 【跨端开…...

微信小程序base64图片与临时路径互相转换
1、base64图片转临时路径 /*** 将base64图片转临时路径* param {*} dataurl* param {*} filename* returns*/base64ImgToFile(dataurl, filename "file") {const base64 dataurl; // base64码const time new Date().getTime();const imgPath wx.env.USER_DATA_P…...

蓝桥杯刷题——day2
蓝桥杯刷题——day2 题目一题干题目解析代码 题目二题干解题思路代码 题目一 题干 三步问题。有个小孩正在上楼梯,楼梯有n阶台阶,小孩一次可以上1阶、2阶或3阶。实现一种方法,计算小孩有多少种上楼梯的方式。结果可能很大,你需要…...

5.删除链表的倒数第N个节点
19.删除链表的倒数第N个节点 题目: 19. 删除链表的倒数第 N 个结点 - 力扣(LeetCode) 分析: 要删除倒数第几个节点,那么我们需要怎么做呢?我们需要定义两个指针,快指针和慢指针,…...

自己总结:selenium高阶知识
全篇大概10000字(含代码),建议阅读时间30min 一、等待机制 如果有一些内容是通过Ajax加载的内容,那就需要等待内容加载完毕才能进行下一步操作。 为了避免人为操作等待,会遇到的问题, selenium将等待转换…...
前端怎么预览pdf
1.背景 后台返回了一个在线的pdf地址,需要我这边去做一个pdf的预览(需求1),并且支持配置是否可以下载(需求2),需要在当前页就能预览(需求3)。之前我写过一篇预览pdf的文…...

activemq 的安装部署
下载 https://activemq.apache.org/components/classic/download/# 在/opt目录下载 wget https://dlcdn.apache.org//activemq/5.18.6/apache-activemq-5.18.6-bin.tar.gz解压 tar -zxvf apache-activemq-5.18.6-bin.tar.gz配置java环境 vim /opt/apache-activemq-5.18.6/b…...
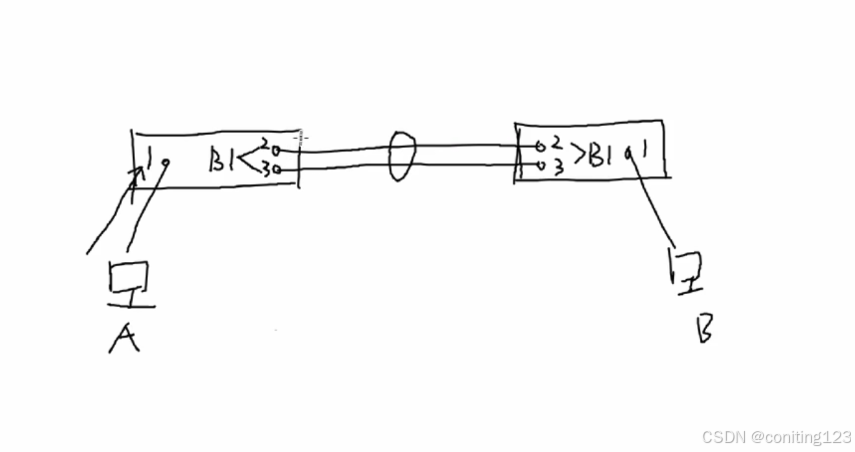
【H3CNE邓方鸣】配置链路聚合+2024.12.11
文章目录 链路聚合作用负载分担分类静态聚合动态聚合 链路聚合作用 定义:把连接到统一交换机上的多个物理端口捆绑为一个逻辑端口 增加链路带宽:聚合组内只要还有物理端口存活,链路就不会中断 提供链路可靠性:避免了STP计算&…...

C语言 学习 日志 递归函数 2024/12/12
C语言 学习 日志 递归函数 介绍: 初始调用:递归函数被首次调用。递归调用:递归函数在其定义中调用自身,创建新的栈帧。基本情况检查:每次递归调用时,检查是否满足基本情况。如果满足,返回结果并开始回溯。…...

【Ubuntu】使用ip link工具创建虚拟局域网并配置?
🦋🦋🦋如何使用ip link工具创建虚拟局域网? sudo ip link add link enx888bd66b7000 name enx.120 type vlan id 120 上述命令使用ip link工具在Linux系统中创建了一个新的虚拟局域网(VLAN)接口,…...
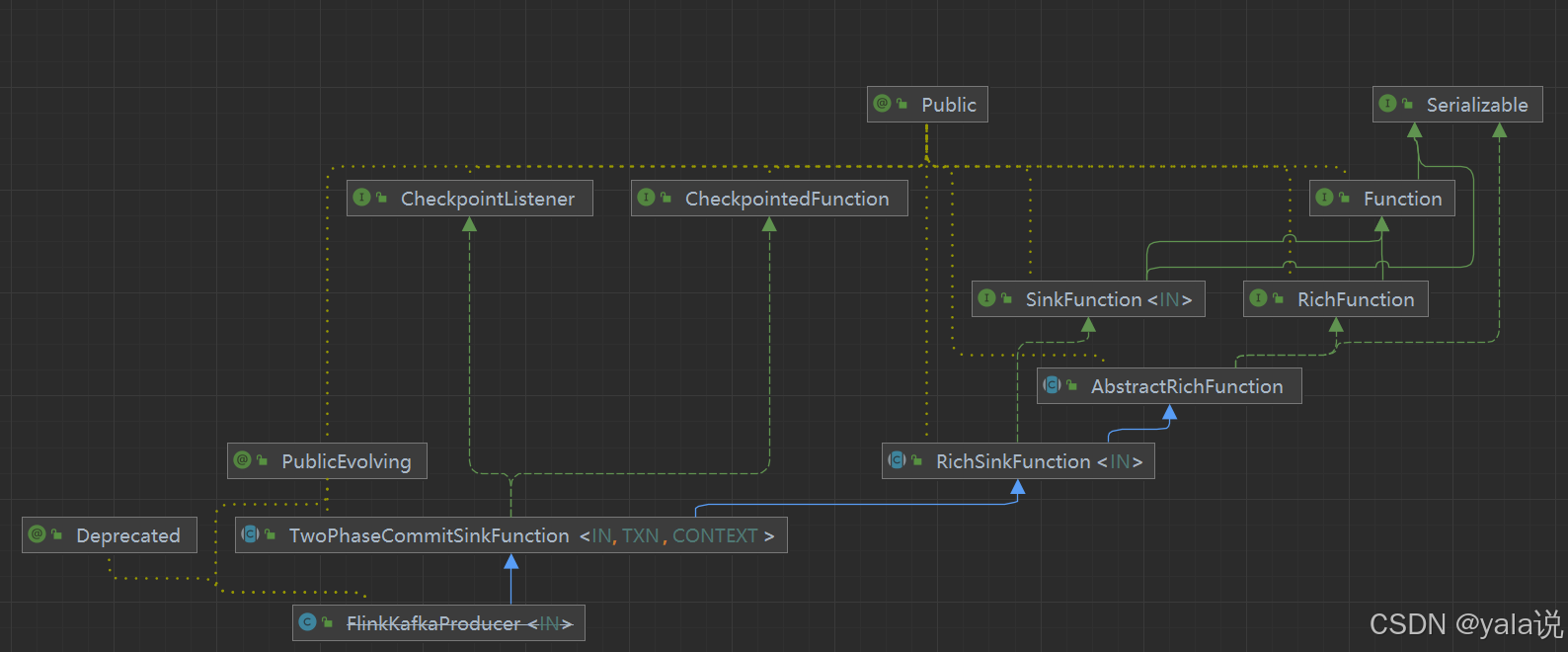
flink sink kafka的事务提交现象猜想
现象 查看flink源码时 sink kafka有事务提交机制,查看源码发现是使用两阶段提交策略,而事务提交是checkpoint完成后才执行,那么如果checkpoint设置间隔时间比较长时,事务未提交之前,后端应该消费不到数据,…...
网络原理03
回顾 应用层:应用程序,数据具体如何使用 传输层:关注起点和终点 网络层:关注路径规划 数据链路层:关注相邻节点的转发 物理层:硬件设备 应用层 应用程序 在应用层,很多时候,…...
每天40分玩转Django:简介和环境搭建
Django简介和环境搭建 一、课程概述 学习项目具体内容预计用时Django概念Django框架介绍、MVC/MTV模式、Django特点60分钟环境搭建Python安装、pip配置、Django安装、IDE选择45分钟创建项目项目结构、基本配置、运行测试75分钟实战练习创建个人博客项目框架60分钟 二、Djang…...

【蓝桥杯最新板】蓝桥杯嵌入式液晶上实现电子时钟
这几年蓝桥杯比赛比较适合学生技能学习,考虑板子功能,提出完成的任务。 要求在液晶完成如下图效果: 主要是实现液晶显示时钟和数字时钟,具体样式可以依据实际情况微调。 实现过程: 1.需要画圆(外圆、内圆…...
【机器学习】基础知识:拟合度(Goodness of Fit)
拟合度概念及意义 拟合度(Goodness of Fit)是衡量统计模型对数据解释能力的指标,用于评价模型对观测数据的拟合效果。在回归分析、分类模型或其他预测模型中,拟合度是模型性能的重要衡量标准。 1. 拟合度的作用 拟合度的主要作用…...

使用Jackson库在Java应用程序中将Map对象转换为JSON数组字符串,以及反向操作
在现代Java应用程序中,特别是使用RESTful Web服务时,经常需要将Java对象转换为JSON格式,反之亦然。 当表示如用户管理系统中的用户列表这样的数据结构时,将Map转换为JSON数组字符串变得非常有用。在这个指南中,我们将…...
深入解析强化学习中的 Generalized Advantage Estimation (GAE)
中文版 深入解析强化学习中的 Generalized Advantage Estimation (GAE) 1. 什么是 Generalized Advantage Estimation (GAE)? 在强化学习中,计算策略梯度的关键在于 优势函数(Advantage Function) 的设计。优势函数 ( A ( s , a ) A(s, a…...

离开wordpress
wordpress确实挺好用的 插件丰富 主题众多 收费的插件也很多 国内的做主题的也挺好 但是服务器跑起来各种麻烦伤脑筋 需要花在维护的时间太多了 如果你的网站持续盈利 你就会更担心访问质量访问速度 而乱七八糟的爬虫黑客 让你的服务器不堪重负 突然有一天看到了静态站…...

盘古信息PCB行业解决方案:以全域场景重构,激活智造新未来
一、破局:PCB行业的时代之问 在数字经济蓬勃发展的浪潮中,PCB(印制电路板)作为 “电子产品之母”,其重要性愈发凸显。随着 5G、人工智能等新兴技术的加速渗透,PCB行业面临着前所未有的挑战与机遇。产品迭代…...

前端导出带有合并单元格的列表
// 导出async function exportExcel(fileName "共识调整.xlsx") {// 所有数据const exportData await getAllMainData();// 表头内容let fitstTitleList [];const secondTitleList [];allColumns.value.forEach(column > {if (!column.children) {fitstTitleL…...

【项目实战】通过多模态+LangGraph实现PPT生成助手
PPT自动生成系统 基于LangGraph的PPT自动生成系统,可以将Markdown文档自动转换为PPT演示文稿。 功能特点 Markdown解析:自动解析Markdown文档结构PPT模板分析:分析PPT模板的布局和风格智能布局决策:匹配内容与合适的PPT布局自动…...

linux 错误码总结
1,错误码的概念与作用 在Linux系统中,错误码是系统调用或库函数在执行失败时返回的特定数值,用于指示具体的错误类型。这些错误码通过全局变量errno来存储和传递,errno由操作系统维护,保存最近一次发生的错误信息。值得注意的是,errno的值在每次系统调用或函数调用失败时…...

uniapp微信小程序视频实时流+pc端预览方案
方案类型技术实现是否免费优点缺点适用场景延迟范围开发复杂度WebSocket图片帧定时拍照Base64传输✅ 完全免费无需服务器 纯前端实现高延迟高流量 帧率极低个人demo测试 超低频监控500ms-2s⭐⭐RTMP推流TRTC/即构SDK推流❌ 付费方案 (部分有免费额度&#x…...

【Oracle】分区表
个人主页:Guiat 归属专栏:Oracle 文章目录 1. 分区表基础概述1.1 分区表的概念与优势1.2 分区类型概览1.3 分区表的工作原理 2. 范围分区 (RANGE Partitioning)2.1 基础范围分区2.1.1 按日期范围分区2.1.2 按数值范围分区 2.2 间隔分区 (INTERVAL Partit…...

NXP S32K146 T-Box 携手 SD NAND(贴片式TF卡):驱动汽车智能革新的黄金组合
在汽车智能化的汹涌浪潮中,车辆不再仅仅是传统的交通工具,而是逐步演变为高度智能的移动终端。这一转变的核心支撑,来自于车内关键技术的深度融合与协同创新。车载远程信息处理盒(T-Box)方案:NXP S32K146 与…...

【电力电子】基于STM32F103C8T6单片机双极性SPWM逆变(硬件篇)
本项目是基于 STM32F103C8T6 微控制器的 SPWM(正弦脉宽调制)电源模块,能够生成可调频率和幅值的正弦波交流电源输出。该项目适用于逆变器、UPS电源、变频器等应用场景。 供电电源 输入电压采集 上图为本设计的电源电路,图中 D1 为二极管, 其目的是防止正负极电源反接, …...

ui框架-文件列表展示
ui框架-文件列表展示 介绍 UI框架的文件列表展示组件,可以展示文件夹,支持列表展示和图标展示模式。组件提供了丰富的功能和可配置选项,适用于文件管理、文件上传等场景。 功能特性 支持列表模式和网格模式的切换展示支持文件和文件夹的层…...

在Zenodo下载文件 用到googlecolab googledrive
方法:Figshare/Zenodo上的数据/文件下载不下来?尝试利用Google Colab :https://zhuanlan.zhihu.com/p/1898503078782674027 参考: 通过Colab&谷歌云下载Figshare数据,超级实用!!࿰…...
