深入 TCP VJ-Style
接着 TCP 的文化内涵 继续扯一会儿。
自 30 instruction TCP receive 往前追溯,论文 Jacobson88 源自第一次拥塞崩溃,这篇著名文档在同时期的另一个缘起是另一篇考古文献 [Zhang86] Why TCP Timers Don’t Work Well,后面这篇文献提出了 TCP RTO 的缺陷,指出:
- RTO 是兜底,不要依赖改进 RTO 来优化性能,本质上 RTT 是测不准的;
- 过大过小的 RTO 要么造成连接近乎中断,要么加剧拥塞,当性能太差时,就近乎故障了;
- 虽然 RTO 计算有固有缺陷,但还是需要 “更好的” RTO 计算方法,比如启发式。
VJ 创造了很多技巧,这些技巧携带了很多神秘的 magic number,现在看来这些技巧被认为理所当然到微不足道,早已没人过问理由(一句 “调一手好参数”),但在 1988 年却是精彩且轰动的,它决定了后续至今的 TCP 演化风格。在 VJ 看来,这些 magic number 都是有理由的,这些理由多数来自 VJ-Style,概括讲,VJ-Style 即对指令的节约。
看 VJ 如何改进 RTO 计算。VJ 简单将 rtt 的移动指数平均换了一种写法(以下按照原始论文的写法):
a = ( 1 − g ) ⋅ a + g ⋅ m a=(1-g)\cdot a+g\cdot m a=(1−g)⋅a+g⋅m => a = a + g ⋅ ( m − a ) a=a+g\cdot (m-a) a=a+g⋅(m−a)
后面的形式直接就有了 “物理意义”,(m - a) 即误差,这个迭代过程展示的是一个校准过程,rtt 不断收敛到正确的值。
由此 (m - a) 作为一个 “误差” 整体直接参与描述 “方差”。VJ-Style 体现在他没有使用真正的方差 Σ ∣ m − a ∣ 2 \Sigma|m-a|^2 Σ∣m−a∣2,理由是它包含乘法,乘方运算,存在整数溢出的风险, “不太容易计算” 一直是 VJ 的动力,VJ-Style 偏爱简单的整数加减和移位运算。
VJ 采用 m d e v 2 = ( Σ ∣ m − a ∣ ) 2 ≥ Σ ∣ m − a ∣ 2 = s d e v 2 mdev^2=(\Sigma|m-a|)^2\ge\Sigma|m-a|^2=sdev^2 mdev2=(Σ∣m−a∣)2≥Σ∣m−a∣2=sdev2 作为替换,他证明了 mdev 和 sdev 之间存在简单关系,从而确认 mdev 作为 “误差” 的直接表示,恰好是 sdev 一个很好的近似。
接下来表示 mdev 均值的方法与表示 rtt 的方法相同,然后用这个 “误差” 来修正 rtt 本身:
E r r = m − a Err=m-a Err=m−a
a = a + g ⋅ E r r a=a+g\cdot Err a=a+g⋅Err
v = v + g ⋅ ( ∣ E r r ∣ − v ) v=v+g\cdot (|Err|-v) v=v+g⋅(∣Err∣−v)
很精彩!对 srtt 移动指数平均的简单变形直接导出了这个闭环。精彩还在继续。
为了 “快速计算”,消除 <1 的 g 的方式是缩放,用 g = 1 2 n g=\dfrac{1}{2^n} g=2n1 进行缩放可以利用简单的移位运算:
2 n ⋅ a = 2 n ⋅ a + E r r 2^n\cdot a=2^n\cdot a+Err 2n⋅a=2n⋅a+Err
2 n ⋅ v = 2 n ⋅ v + ( ∣ E r r ∣ − v ) 2^n \cdot v=2^n \cdot v+(|Err|-v) 2n⋅v=2n⋅v+(∣Err∣−v)
剩下的事只是选择 n,而 n = 3 时,效果最接近 RFC793 的建议,由此,VJ 完成了对 rtt 计算的一次优化,下面的代码直到现在还在被各种 TCP 实现几乎照抄:
/* 更新平均估计 */
m -= (sa >> 3);
sa += m;
/* 更新偏差估计 */
if (m < 0)m = -m;
m -= (sv >> 3);
sv += m;
Linux 内核的 tcp_rtt_estimator 也在采用。
剩下的计算 RTO 自然水到渠成,它由 rtt 加上 “误差” 的一定增益组成:
R T O = a + 4 ⋅ v RTO=a+4\cdot v RTO=a+4⋅v
这里的 4 来自现实数据统计律,因为它不太小,足够大。仍然是为了便于计算,v 的 g 采用了 1/4:
2 3 ⋅ a = 2 3 ⋅ a + E r r 2^3\cdot a=2^3\cdot a+Err 23⋅a=23⋅a+Err
2 2 ⋅ v = 2 2 ⋅ v + ( ∣ E r r ∣ − v ) 2^2 \cdot v=2^2 \cdot v+(|Err|-v) 22⋅v=22⋅v+(∣Err∣−v)
m -= (sa >> 3);
sa += m;
if (m < 0)m = -m;
m -= (sv >> 2);
sv += m;
rto = (sa >> 3) + sv;
这完美解决了 Lixia Zhang 在 Zhang86 提出的问题,至今工作良好。
RTO 的魔数 4 还来自 VJ 慢启动的理论分析。如果在慢启动轮次结束时计算的重传超时小于等于下一轮的实际 rtt,就会发生虚假重传。最坏情况下,假设所有延迟都由窗口大小的数据排队引发,延迟将每轮翻倍(因为窗口大小翻倍),因此 R i + 1 = 2 ⋅ R i R_{i+1}=2\cdot R_i Ri+1=2⋅Ri,而 V i = R i − R i − 1 = R i 2 V_i=R_i-R_{i-1}=\dfrac{R_i}{2} Vi=Ri−Ri−1=2Ri,所以 R T O i = R i + R i + 4 V i = 3 R i > 2 R i > R i + 1 RTO_i=R_i+R_i+4V_i=3R_i>2R_i>R_{i+1} RTOi=Ri+Ri+4Vi=3Ri>2Ri>Ri+1,因此虚假重传将不会发生,好精彩!
AIMD 的 Additive Increase 过程每个 ACK 导致 w 增加 1 / w,这导致了除法运算,不仅如此,VJ 建议不要发送 MTU 分数倍的数据包,因为这会降低载荷率,二力合一,VJ-Style 的 AIMD 采用计数方式简单避免了除法运算:
snd_cwnd_cnt ++;
if (snd_cwnd_cnt > cwnd)cwnd ++;
先写到这,其余的参考 RFC1072 后面再说。
浙江温州皮鞋湿,下雨进水不会胖。
相关文章:

深入 TCP VJ-Style
接着 TCP 的文化内涵 继续扯一会儿。 自 30 instruction TCP receive 往前追溯,论文 Jacobson88 源自第一次拥塞崩溃,这篇著名文档在同时期的另一个缘起是另一篇考古文献 [Zhang86] Why TCP Timers Don’t Work Well,后面这篇文献提出了 TCP…...

go高性能单机缓存项目
代码 // Copyright 2021 ByteDance Inc. // // Licensed under the Apache License, Version 2.0 (the "License"); // you may not use this file except in compliance with the License. // You may obtain a copy of the License at // // http://www.apach…...

数据结构绪论
文章目录 绪论数据结构三要素算法 🏡作者主页:点击! 🤖数据结构专栏:点击! ⏰️创作时间:2024年12月12日01点09分 绪论 数据是信息的载体,描述客观事物属性的数、字符及所有能输入…...

前端开发常用四大框架学习难度咋样?
前端开发常用四大框架指的是 jQuery vue react angular jQuery: 学习难度:相对较低特点:jQuery 是一个快速、小巧、功能丰富的 JavaScript 库。它使得 HTML 文档遍历和操作、事件处理、动画和 Ajax 交互更加简单。适用场景&a…...

OWASP 十大安全漏洞的原理
1. Broken Access Control(访问控制失效) 原理:应用程序未正确实施权限检查,导致攻击者通过篡改请求、强制浏览或权限提升等手段绕过访问控制。 攻击手段: 修改 URL、HTML、或 API 请求以访问未经授权的资源。 删除…...

论文 | ChunkRAG: Novel LLM-Chunk Filtering Method for RAG Systems
本文详细介绍了一种新颖的检索增强生成(Retrieval-Augmented Generation, RAG)系统方法——ChunkRAG,该方法通过对文档的分块语义分析和过滤显著提升了生成系统的准确性和可靠性。 1. 研究背景与问题 1.1 检索增强生成的意义 RAG系统结合…...

ORACLE SQL思路: 多行数据有相同字段就合并成一条数据 分页展示
数据 分数表: 学号,科目名(A,B,C),分数 需求 分页列表展示, 如果一个学号的科目有相同的分数, 合并成一条数据,用 拼接 科目名 ORACLE SQL 实现 SELECT Z.*, SUBSTR(DECODE(f…...
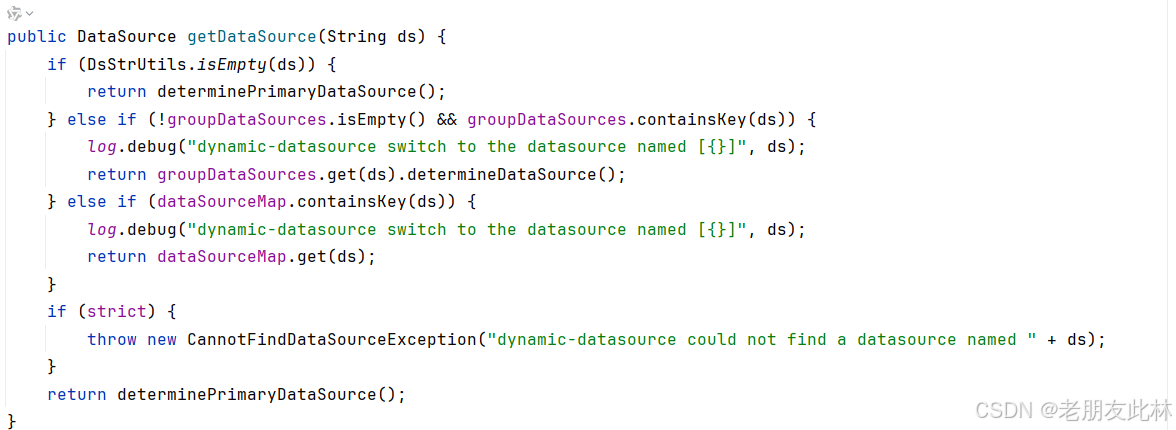
SpringBoot 手动实现动态切换数据源 DynamicSource (中)
大家好,我是此林。 SpringBoot 手动实现动态切换数据源 DynamicSource (上)-CSDN博客 在上一篇博客中,我带大家手动实现了一个简易版的数据源切换实现,方便大家理解数据源切换的原理。今天我们来介绍一个开源的数据源…...
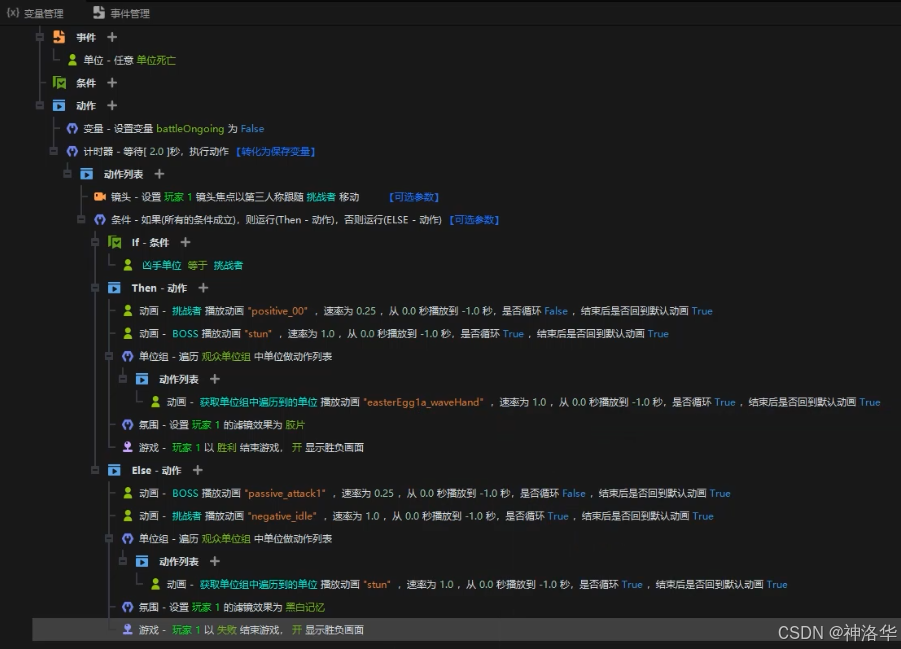
y3编辑器教学5:触发器2 案例演示
文章目录 一、探索1.1 ECA1.1.1 ECA的定义1.1.2 使用触发器实现瞬间移动效果 1.2 变量1.2.1 什么是变量1.2.2 使用变量存储碎片收集数量并展现 1.3 if语句(魔法效果挂接)1.3.1 地形设置1.3.2 编写能量灌注逻辑1.3.3 编写能量灌注后,实现传送逻…...

数值分析——插值法(二)
文章目录 前言一、Hermite插值1.两点三次Hermite插值2.两点三次Hermite插值的推广3.非标准型Hermite插值 二、三次样条插值1.概念2.三弯矩方程 前言 之前写过Lagrange插值与Newton插值法的内容,这里介绍一些其他的插值方法,顺便复习数值分析. 一、Hermi…...
杨振宁大学物理视频中黄色的字,c#写程序去掉
先看一下效果:(还有改进的余地) 写了个程序消除杨振宁大学物理中黄色的字 我的方法是笨方法,也比较刻板。 1,首先想到,把屏幕打印下来。c#提供了这样一个函数: Bitmap bmp new Bitmap(640, 48…...

uni-app 设置缓存过期时间【跨端开发系列】
🔗 uniapp 跨端开发系列文章:🎀🎀🎀 uni-app 组成和跨端原理 【跨端开发系列】 uni-app 各端差异注意事项 【跨端开发系列】uni-app 离线本地存储方案 【跨端开发系列】uni-app UI库、框架、组件选型指南 【跨端开…...

微信小程序base64图片与临时路径互相转换
1、base64图片转临时路径 /*** 将base64图片转临时路径* param {*} dataurl* param {*} filename* returns*/base64ImgToFile(dataurl, filename "file") {const base64 dataurl; // base64码const time new Date().getTime();const imgPath wx.env.USER_DATA_P…...

蓝桥杯刷题——day2
蓝桥杯刷题——day2 题目一题干题目解析代码 题目二题干解题思路代码 题目一 题干 三步问题。有个小孩正在上楼梯,楼梯有n阶台阶,小孩一次可以上1阶、2阶或3阶。实现一种方法,计算小孩有多少种上楼梯的方式。结果可能很大,你需要…...

5.删除链表的倒数第N个节点
19.删除链表的倒数第N个节点 题目: 19. 删除链表的倒数第 N 个结点 - 力扣(LeetCode) 分析: 要删除倒数第几个节点,那么我们需要怎么做呢?我们需要定义两个指针,快指针和慢指针,…...

自己总结:selenium高阶知识
全篇大概10000字(含代码),建议阅读时间30min 一、等待机制 如果有一些内容是通过Ajax加载的内容,那就需要等待内容加载完毕才能进行下一步操作。 为了避免人为操作等待,会遇到的问题, selenium将等待转换…...
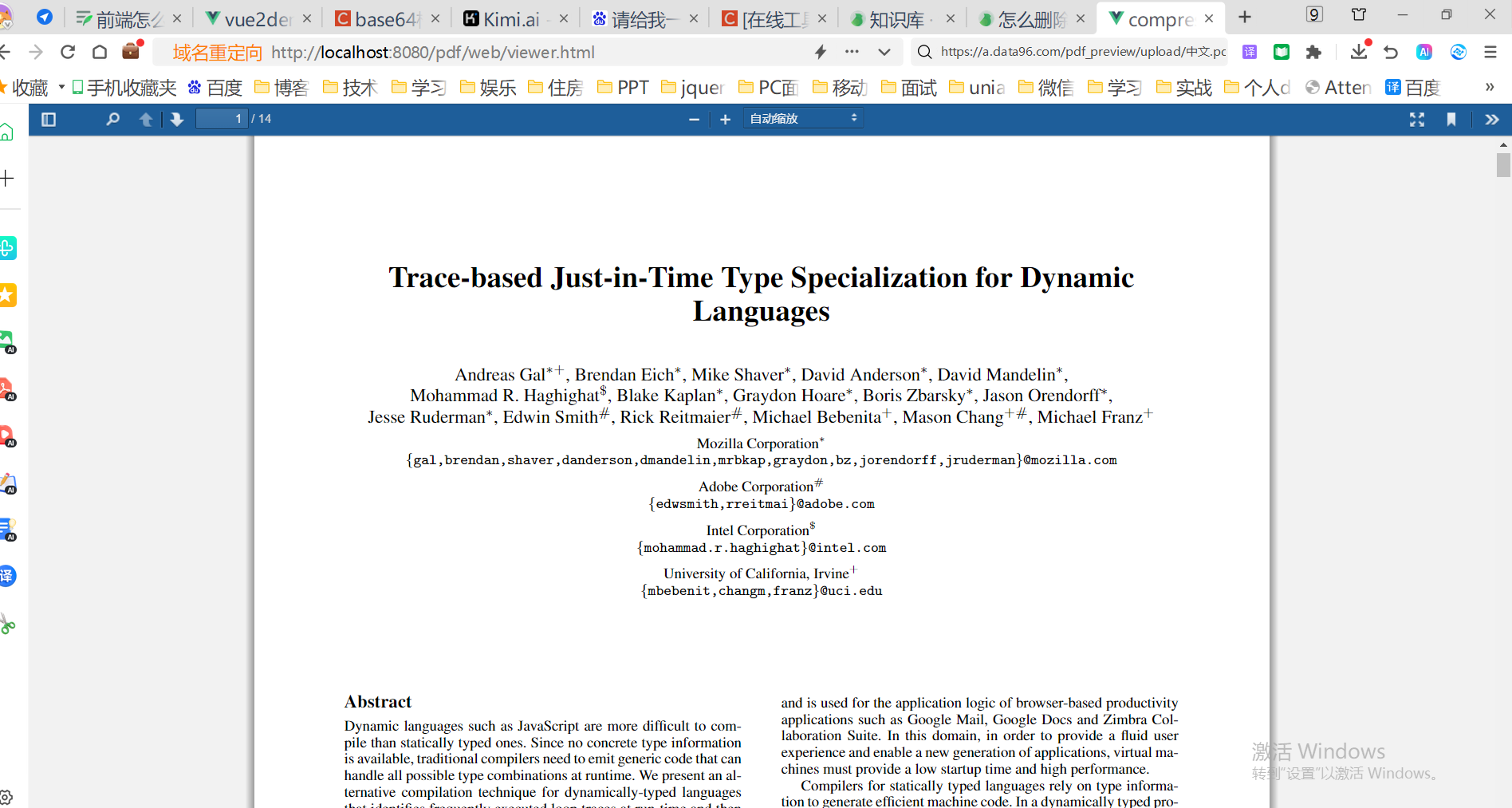
前端怎么预览pdf
1.背景 后台返回了一个在线的pdf地址,需要我这边去做一个pdf的预览(需求1),并且支持配置是否可以下载(需求2),需要在当前页就能预览(需求3)。之前我写过一篇预览pdf的文…...

activemq 的安装部署
下载 https://activemq.apache.org/components/classic/download/# 在/opt目录下载 wget https://dlcdn.apache.org//activemq/5.18.6/apache-activemq-5.18.6-bin.tar.gz解压 tar -zxvf apache-activemq-5.18.6-bin.tar.gz配置java环境 vim /opt/apache-activemq-5.18.6/b…...
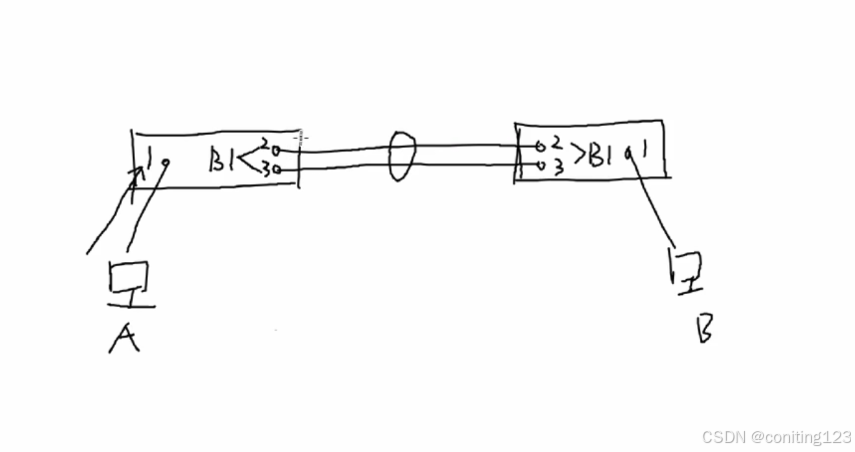
【H3CNE邓方鸣】配置链路聚合+2024.12.11
文章目录 链路聚合作用负载分担分类静态聚合动态聚合 链路聚合作用 定义:把连接到统一交换机上的多个物理端口捆绑为一个逻辑端口 增加链路带宽:聚合组内只要还有物理端口存活,链路就不会中断 提供链路可靠性:避免了STP计算&…...

C语言 学习 日志 递归函数 2024/12/12
C语言 学习 日志 递归函数 介绍: 初始调用:递归函数被首次调用。递归调用:递归函数在其定义中调用自身,创建新的栈帧。基本情况检查:每次递归调用时,检查是否满足基本情况。如果满足,返回结果并开始回溯。…...

OpenLayers 可视化之热力图
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 热力图(Heatmap)又叫热点图,是一种通过特殊高亮显示事物密度分布、变化趋势的数据可视化技术。采用颜色的深浅来显示…...

【JVM】- 内存结构
引言 JVM:Java Virtual Machine 定义:Java虚拟机,Java二进制字节码的运行环境好处: 一次编写,到处运行自动内存管理,垃圾回收的功能数组下标越界检查(会抛异常,不会覆盖到其他代码…...
:滤镜命令)
ffmpeg(四):滤镜命令
FFmpeg 的滤镜命令是用于音视频处理中的强大工具,可以完成剪裁、缩放、加水印、调色、合成、旋转、模糊、叠加字幕等复杂的操作。其核心语法格式一般如下: ffmpeg -i input.mp4 -vf "滤镜参数" output.mp4或者带音频滤镜: ffmpeg…...

从零实现STL哈希容器:unordered_map/unordered_set封装详解
本篇文章是对C学习的STL哈希容器自主实现部分的学习分享 希望也能为你带来些帮助~ 那咱们废话不多说,直接开始吧! 一、源码结构分析 1. SGISTL30实现剖析 // hash_set核心结构 template <class Value, class HashFcn, ...> class hash_set {ty…...

HashMap中的put方法执行流程(流程图)
1 put操作整体流程 HashMap 的 put 操作是其最核心的功能之一。在 JDK 1.8 及以后版本中,其主要逻辑封装在 putVal 这个内部方法中。整个过程大致如下: 初始判断与哈希计算: 首先,putVal 方法会检查当前的 table(也就…...

处理vxe-table 表尾数据是单独一个接口,表格tableData数据更新后,需要点击两下,表尾才是正确的
修改bug思路: 分别把 tabledata 和 表尾相关数据 console.log() 发现 更新数据先后顺序不对 settimeout延迟查询表格接口 ——测试可行 升级↑:async await 等接口返回后再开始下一个接口查询 ________________________________________________________…...

Python Einops库:深度学习中的张量操作革命
Einops(爱因斯坦操作库)就像给张量操作戴上了一副"语义眼镜"——让你用人类能理解的方式告诉计算机如何操作多维数组。这个基于爱因斯坦求和约定的库,用类似自然语言的表达式替代了晦涩的API调用,彻底改变了深度学习工程…...

【学习笔记】erase 删除顺序迭代器后迭代器失效的解决方案
目录 使用 erase 返回值继续迭代使用索引进行遍历 我们知道类似 vector 的顺序迭代器被删除后,迭代器会失效,因为顺序迭代器在内存中是连续存储的,元素删除后,后续元素会前移。 但一些场景中,我们又需要在执行删除操作…...

什么是VR全景技术
VR全景技术,全称为虚拟现实全景技术,是通过计算机图像模拟生成三维空间中的虚拟世界,使用户能够在该虚拟世界中进行全方位、无死角的观察和交互的技术。VR全景技术模拟人在真实空间中的视觉体验,结合图文、3D、音视频等多媒体元素…...

Python训练营-Day26-函数专题1:函数定义与参数
题目1:计算圆的面积 任务: 编写一个名为 calculate_circle_area 的函数,该函数接收圆的半径 radius 作为参数,并返回圆的面积。圆的面积 π * radius (可以使用 math.pi 作为 π 的值)要求:函数接收一个位置参数 radi…...
