求解球面的一组正交标架
目录
- 求解球面的一组正交标架
求解球面的一组正交标架
球面 r ( u , v ) = ( a cos u cos v , a cos u sin v , a sin u ) \mathbf{r}(u,v)=\left(a\cos u\cos v,a\cos u\sin v,a\sin u\right) r(u,v)=(acosucosv,acosusinv,asinu),
求得
r u = ( − a sin u cos v , − a sin u sin v , a cos u ) r v = ( − a cos u sin v , a cos u cos v , 0 ) \mathbf{r}_u=(-a\sin u\cos v,-a\sin u\sin v,a\cos u)\\\mathbf{r}_v=(-a\cos u\sin v,a\cos u\cos v,0) ru=(−asinucosv,−asinusinv,acosu)rv=(−acosusinv,acosucosv,0)
计算得
E = a 2 , F = 0 , G = a 2 cos 2 u E=a^2,F=0,G=a^2\cos^2u E=a2,F=0,G=a2cos2u
于是选取
e 1 = 1 a r u = ( − sin u cos v , − sin u sin v , cos u ) \mathbf{e}_{1}=\frac{1}{a}\mathbf{r}_{u}=(-\sin u\cos v,-\sin u\sin v,\cos u) e1=a1ru=(−sinucosv,−sinusinv,cosu)
e 2 = 1 a cos u r v = ( − sin v , cos v , 0 ) \mathbf{e}_2=\frac1{a\cos u}\mathbf{r}_v=(-\sin v,\cos v,0) e2=acosu1rv=(−sinv,cosv,0)
求其外积为
e 3 = n = ( − cos u cos v , − cos u sin v , − sin u ) \mathbf{e}_3=\mathbf{n}=(-\cos u\cos v,-\cos u\sin v,-\sin u) e3=n=(−cosucosv,−cosusinv,−sinu)
这就找到了球面的一组正交活动标架。
相关文章:

求解球面的一组正交标架
目录 求解球面的一组正交标架 求解球面的一组正交标架 球面 r ( u , v ) ( a cos u cos v , a cos u sin v , a sin u ) \mathbf{r}(u,v)\left(a\cos u\cos v,a\cos u\sin v,a\sin u\right) r(u,v)(acosucosv,acosusinv,asinu), 求得 r u ( − a sin u c…...

php.ini 文件上传/执行时间/部分配置新手教程
1、上传文件大小配置 一般需要同时配置“upload_max_filesize”、“post_max_size”,配置格式如下: file_uploads On ;是否允许HTTP文件上传 upload_max_filesize 2M ;设置单个文件上传的最大尺寸 post_max_size 8M ;设置 POST 请求体的最大尺寸&am…...

【Leetcode Top 100】102. 二叉树的层序遍历
问题背景 给你二叉树的根节点 r o o t root root,返回其节点值的 层序遍历 。 (即逐层地,从左到右访问所有节点)。 数据约束 树中节点数目在范围 [ 0 , 2000 ] [0, 2000] [0,2000] 内 − 1000 ≤ N o d e . v a l ≤ 1000 -1…...

【C++笔记】AVL树
前言 各位读者朋友们大家好,上期我们讲解了map和set这两大容器的使用,这一期我们讲解最早的平衡二叉搜索树——AVL树。 目录 前言一. AVL树的概念二. AVL树的实现2.1 AVL树的结构2.2 AVL树的插入2.2.1 AVL树插入一个值的大致过程2.2.2 平衡因子的更新2…...

【竞技宝】LOL:JDG官宣yagao离队
北京时间2024年12月13日,在英雄联盟S14全球总决赛结束之后,各大赛区都已经进入了休赛期,目前休赛期也快进入尾声,LPL大部分队伍都开始陆续官宣转会期的动向,其中JDG就在近期正式官宣中单选手yagao离队,而后者大概率将直接选择退役。 近日,JDG战队在官方微博上连续发布阵容变动消…...

双目摄像头标定方法
打开matlab 找到这个标定 将双目左右目拍的图像上传(左右目最好不少于20张) 等待即可 此时已经完成标定,左下角为反投影误差,右边为外参可视化 把这些误差大的删除即可。 点击导出 此时回到主页面,即可看到成功导出 Ca…...

相差不超过k的最多数,最长公共子序列(一),排序子序列,体操队形,青蛙过河
相差不超过k的最多数 链接:相差不超过k的最多数 来源:牛客网 题目描述: 给定一个数组,选择一些数,要求选择的数中任意两数差的绝对值不超过 𝑘 。问最多能选择多少个数? 输入描述: 第一行输入两个正整…...
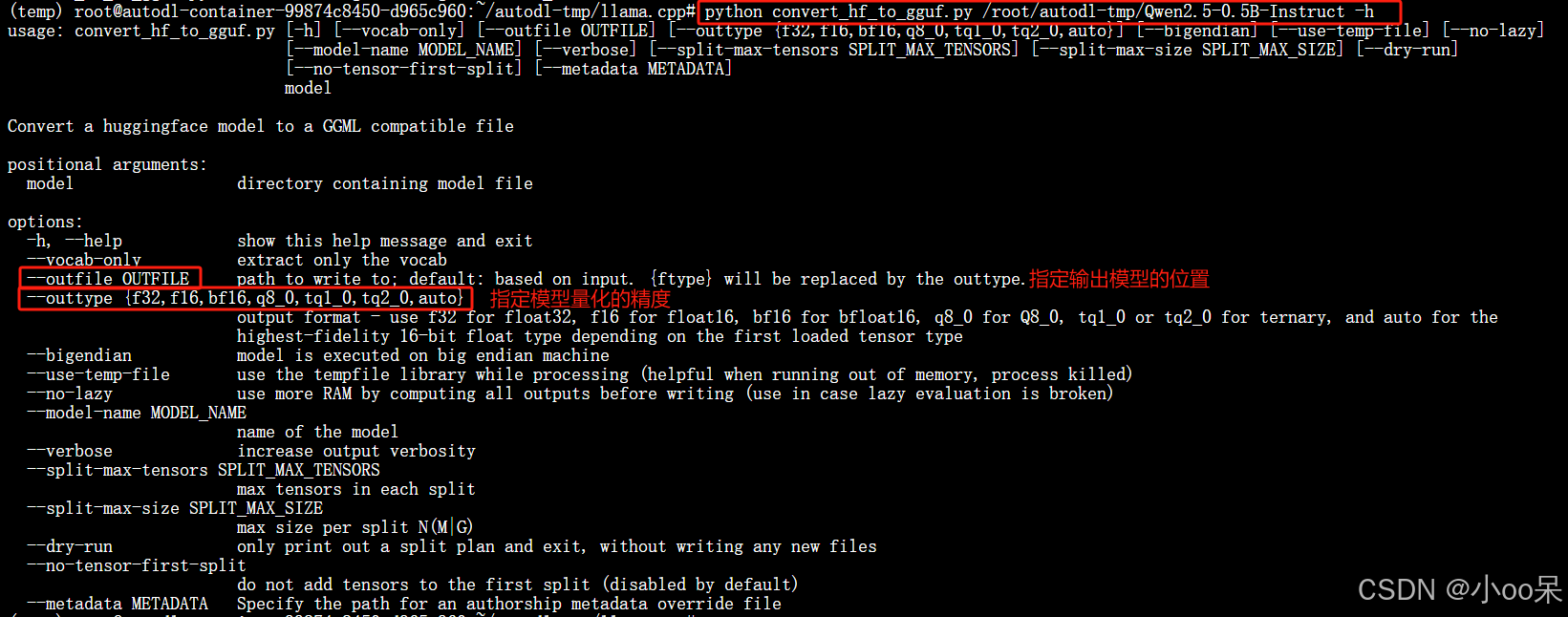
【自然语言处理与大模型】使用llama.cpp将HF格式大模型转换为GGUF格式
llama.cpp的主要目标是在本地和云端的各种硬件上以最小的设置和最先进的性能实现LLM推理。是一个专为大型语言模型(LLM)设计的高性能推理框架,完全使用C和C编写,没有外部依赖,这使得它可以很容易地被移植到不同的操作系…...

MongoDB存储照片和文件存储照片的区别在那里?
一、维度对比 比较维度MongoDB存储照片文件系统存储照片数据模型使用文档存储数据,可以存储不同结构的照片。以文件的形式存储照片,每个文件独立存在。性能高效的数据检索,适用于大规模应用程序中的高效检索和访问。但在处理大量高分辨率图片…...

协变量的概念
协变量的概念 协变量的概念 协变量(Covariate)是在统计分析和研究中,与因变量(被研究的主要变量)相关,并且可能对因变量产生影响的其他变量。它不是研究的主要关注对象,但需要在分析过程中被考虑进去,因为它可能会混淆或改变自变量与因变量之间的关系。举例说明 教育研…...

【[LeetCode每日一题】Leetcode 1768.交替合并字符串
Leetcode 1768.交替合并字符串 题目描述: 给定两个字符串 word1 和 word2,以交替的方式将它们合并成一个新的字符串。即,第一个字符来自 word1,第二个字符来自 word2,第三个字符来自 word1,依此类推。如果…...

SRT协议学习
SRT(Secure Reliable Transport)协议是一种开源的视频传输协议,旨在提供安全,可靠,低延迟的视频流传输。以下是SRT协议的一些关键的工作原理。 1 安全传输,SRT通过使用AES加密和数据完整性验证来确保数据的安全传输。它可以在不信…...

南昌大学《2024年837自动控制原理真题》 (完整版)
本文内容,全部选自自动化考研联盟的:《南昌大学873自控考研资料》的真题篇。后续会持续更新更多学校,更多年份的真题,记得关注哦~ 目录 2024年真题 Part1:2024年完整版真题 2024年真题...

ASP.NET Core 应用程序的启动与配置:Program.cs 文件的全面解析
ASP.NET Core 应用程序的启动与配置:Program.cs 文件的全面解析 Program.cs 是 ASP.NET Core 应用程序的入口点,负责应用程序的启动和配置。以下是 Program.cs 文件中完成的主要工作,按逻辑步骤进行总结: 1. 创建和配置主机环境…...

2020-12-02 数字过滤
缘由 C语言 数组:数字过滤-CSDN问答 void chuli(int n15236) {int aa[47]{0},j0,m0;while(n)aa[j]n%10,n/10;while(j)if(aa[--j]%2)m*10,maa[j];cout << m << ends; } void 数字过滤(int n 15236) {int aa[47]{0}, j 0, m 0;while (…...
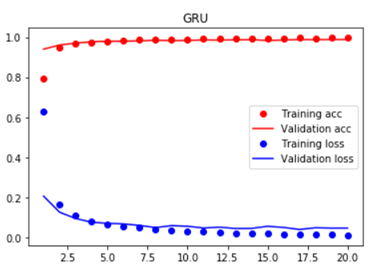
长短期记忆神经网络(LSTM)介绍
1、应用现状 长短期记忆神经网络(LSTM)是一种特殊的循环神经网络(RNN)。原始的RNN在训练中,随着训练时间的加长以及网络层数的增多,很容易出现梯度爆炸或者梯度消失的问题,导致无法处理较长序列数据,从而无…...

数据结构 ——二叉树转广义表
数据结构 ——二叉树转广义表 1、树转广义表 如下一棵树,转换为广义表 root(c(a()(b()()))(e(d()())(f()(j(h()())())))) (根(左子树)(右子树)) 代码实现 #include<stdio.h> #include<stdlib.h>//保存…...

chattts生成的音频与字幕修改完善,每段字幕对应不同颜色的视频,准备下一步插入视频。
上一节中,实现了先生成一个固定背景的与音频长度一致的视频,然后插入字幕。再合并成一个视频的方法。 但是:这样有点单了,所以: 1.根据字幕的长度先生成视频片断 2.在片段上加上字幕。 3.合并所有片断,…...

数据结构开始——时间复杂度和空间复杂度知识点笔记总结
好了,经过了漫长的时间学习c语言语法知识,现在我们到了数据结构的学习。 首先,我们得思考一下 什么是数据结构? 数据结构(Data Structure)是计算机存储、组织数据的方式,指相互之间存在一种或多种特定关系的数据元素…...

路由策略与策略路由
路由策略 常用有Router-Policy,Filter-Policy等 控制路由是否可达,通过修改路由条目相关参数影响流量的转发 基于控制平面,会影响路由表表项,但只能基于目地址进行策略判定,于路由协议相结合使用 Router-Policy …...

基于FPGA的PID算法学习———实现PID比例控制算法
基于FPGA的PID算法学习 前言一、PID算法分析二、PID仿真分析1. PID代码2.PI代码3.P代码4.顶层5.测试文件6.仿真波形 总结 前言 学习内容:参考网站: PID算法控制 PID即:Proportional(比例)、Integral(积分&…...

大话软工笔记—需求分析概述
需求分析,就是要对需求调研收集到的资料信息逐个地进行拆分、研究,从大量的不确定“需求”中确定出哪些需求最终要转换为确定的“功能需求”。 需求分析的作用非常重要,后续设计的依据主要来自于需求分析的成果,包括: 项目的目的…...

【人工智能】神经网络的优化器optimizer(二):Adagrad自适应学习率优化器
一.自适应梯度算法Adagrad概述 Adagrad(Adaptive Gradient Algorithm)是一种自适应学习率的优化算法,由Duchi等人在2011年提出。其核心思想是针对不同参数自动调整学习率,适合处理稀疏数据和不同参数梯度差异较大的场景。Adagrad通…...

基于Uniapp开发HarmonyOS 5.0旅游应用技术实践
一、技术选型背景 1.跨平台优势 Uniapp采用Vue.js框架,支持"一次开发,多端部署",可同步生成HarmonyOS、iOS、Android等多平台应用。 2.鸿蒙特性融合 HarmonyOS 5.0的分布式能力与原子化服务,为旅游应用带来…...

【单片机期末】单片机系统设计
主要内容:系统状态机,系统时基,系统需求分析,系统构建,系统状态流图 一、题目要求 二、绘制系统状态流图 题目:根据上述描述绘制系统状态流图,注明状态转移条件及方向。 三、利用定时器产生时…...

在web-view 加载的本地及远程HTML中调用uniapp的API及网页和vue页面是如何通讯的?
uni-app 中 Web-view 与 Vue 页面的通讯机制详解 一、Web-view 简介 Web-view 是 uni-app 提供的一个重要组件,用于在原生应用中加载 HTML 页面: 支持加载本地 HTML 文件支持加载远程 HTML 页面实现 Web 与原生的双向通讯可用于嵌入第三方网页或 H5 应…...

HDFS分布式存储 zookeeper
hadoop介绍 狭义上hadoop是指apache的一款开源软件 用java语言实现开源框架,允许使用简单的变成模型跨计算机对大型集群进行分布式处理(1.海量的数据存储 2.海量数据的计算)Hadoop核心组件 hdfs(分布式文件存储系统)&a…...

【VLNs篇】07:NavRL—在动态环境中学习安全飞行
项目内容论文标题NavRL: 在动态环境中学习安全飞行 (NavRL: Learning Safe Flight in Dynamic Environments)核心问题解决无人机在包含静态和动态障碍物的复杂环境中进行安全、高效自主导航的挑战,克服传统方法和现有强化学习方法的局限性。核心算法基于近端策略优化…...

招商蛇口 | 执笔CID,启幕低密生活新境
作为中国城市生长的力量,招商蛇口以“美好生活承载者”为使命,深耕全球111座城市,以央企担当匠造时代理想人居。从深圳湾的开拓基因到西安高新CID的战略落子,招商蛇口始终与城市发展同频共振,以建筑诠释对土地与生活的…...

手机平板能效生态设计指令EU 2023/1670标准解读
手机平板能效生态设计指令EU 2023/1670标准解读 以下是针对欧盟《手机和平板电脑生态设计法规》(EU) 2023/1670 的核心解读,综合法规核心要求、最新修正及企业合规要点: 一、法规背景与目标 生效与强制时间 发布于2023年8月31日(OJ公报&…...
