最短路----Dijkstra算法详解
简介
迪杰斯特拉(Dijkstra)算法是一种用于在加权图中找到单个源点到所有其他顶点的最短路径的算法。它是由荷兰计算机科学家艾兹格·迪科斯彻(Edsger Dijkstra)在1956年提出的。Dijkstra算法适用于处理带有非负权重的图。迪杰斯特拉算法主要特点是从起始点开始,采用贪心算法,每次遍历到始点距离最近且未访问过的顶点的邻接节点,直到扩展到终点为止。适用的是单源路径最短路问题,对于多源则采用弗洛伊德(Floyd)算法
Dijkstra算法原理
-
初始化:
- 创建一个距离数组
dist,用来存储从起始节点到每个节点的最短距离,初始时将起始节点的距离设为0,其余节点设为无穷大。 - 创建一个优先队列(通常使用最小堆)来存储待处理的节点,初始时将起始节点加入队列。
- 创建一个距离数组
-
处理节点:
- 从优先队列中取出距离最小的节点,标记为已处理。
- 对于该节点的每个邻接节点,计算从起始节点到该邻接节点的距离。如果这个距离小于当前记录的距离,则更新距离并将该邻接节点加入优先队列。
-
重复:
- 重复步骤2,直到优先队列为空,或者所有节点都被处理。
如果还看不明白,请看下图

举个栗子
示例图
图的邻接表表示
- 节点0到节点1的边权重为1
- 节点0到节点2的边权重为4
- 节点1到节点2的边权重为2
- 节点1到节点3的边权重为5
- 节点2到节点4的边权重为1
- 节点4到节点3的边权重为1
Dijkstra算法执行过程
假设我们从节点0开始,以下是dist和visited数组在每一步的变化:
-
初始化:
dist = [0, ∞, ∞, ∞, ∞](从起始节点0到其他节点的距离)visited = [false, false, false, false, false](所有节点未被访问)
-
处理节点0:
- 当前节点:0
- 更新邻接节点1和2:
dist[1] = 1(0到1的距离)dist[2] = 4(0到2的距离)
- 更新后的数组:
dist = [0, 1, 4, ∞, ∞]visited = [true, false, false, false, false]
-
处理节点1(下一个最小距离的节点):
- 当前节点:1
- 更新邻接节点2和3:
dist[2] = min(4, 1 + 2) = 3(更新0到2的距离)dist[3] = 1 + 5 = 6(更新0到3的距离)
- 更新后的数组:
dist = [0, 1, 3, 6, ∞]visited = [true, true, false, false, false]
-
处理节点2:
- 当前节点:2
- 更新邻接节点4:
dist[4] = min(∞, 3 + 1) = 4(更新0到4的距离)
- 更新后的数组:
dist = [0, 1, 3, 6, 4]visited = [true, true, true, false, false]
-
处理节点4:
- 当前节点:4
- 更新邻接节点3:
dist[3] = min(6, 4 + 1) = 5(更新0到3的距离)
- 更新后的数组:
dist = [0, 1, 3, 5, 4]visited = [true, true, true, false, true]
-
处理节点3:
- 当前节点:3
- 由于3没有未访问的邻接节点,算法结束。
- 最终的
dist数组为:dist = [0, 1, 3, 5, 4](从节点0到各个节点的最短距离)
visited数组为:visited = [true, true, true, true, true](所有节点均已访问)
最终结果
- 从节点0到节点1的最短距离是1
- 从节点0到节点2的最短距离是3
- 从节点0到节点3的最短距离是5
- 从节点0到节点4的最短距离是4
这个过程展示了Dijkstra算法如何逐步更新每个节点的最短路径,并标记已访问的节点。
代码实现
#include<iostream>
using namespace std;
int n,e,s;//n个顶点,e条边,s是起点
int dis[101];//dis[i]起点到i的最短距离
int vis[101];//标记是否找到
int edge[101][101];//记录路径i->j有路径
int main()
{cin>>n>>e;for(int i=1;i<=n;i++){dis[i]=100000;}for(int i=1;i<=e;i++){//邻接矩阵存储int a,b,c;cin>>a>>b>>c;edge[a][b]=c;}cin>>s;dis[s]=0;//起点到起点不需要代价for(int i=1;i<=n;i++){int minn=inf,minx;for(int j=1;j<=n;j++){if(dis[j]<minn&&vis[j]==0){//寻找此点到其他点的最小距离minn=dis[j];minx=j;}}vis[minx]=1;//标记到达的最小点for(int j=1;j<=n;j++){if(edge[minx][j]>0)//有边的话 {if(minn+edge[minx][j]<dis[j]){dis[j]=minn+edge[minx][j];//更新以最小距离点最为中转点的最小距离}}}}for(int i=1;i<=n;i++){//打印最短距离cout<<dis[i]<<" ";}return 0;
}相关文章:

最短路----Dijkstra算法详解
简介 迪杰斯特拉(Dijkstra)算法是一种用于在加权图中找到单个源点到所有其他顶点的最短路径的算法。它是由荷兰计算机科学家艾兹格迪科斯彻(Edsger Dijkstra)在1956年提出的。Dijkstra算法适用于处理带有非负权重的图。迪杰斯特拉…...

ORB-SLAM3源码学习:G2oTypes.cc: void EdgeInertial::computeError 计算预积分残差
前言 这部分函数涉及了g2o的内容以及IMU相关的推导内容,需要你先去进行这部分的学习。 1.函数声明 void EdgeInertial::computeError() 2.函数定义 涉及到的IMU的公式: {// TODO Maybe Reintegrate inertial measurments when difference between …...

Unity协程机制详解
Unity的协程(Coroutine)是一种异步编程的机制,允许在多个帧之间分割代码的执行,而不阻塞主线程。与传统的多线程不同,Unity的协程在主线程中运行,并不会开启新的线程。 什么是协程? 协程是一种…...

2024年【高压电工】最新解析及高压电工考试总结
高压电工考试是电力行业从业人员必须通过的资格考试之一,它不仅检验了考生对高压电技术的掌握程度,还考验了考生在实际操作中的安全意识和应急处理能力。为了帮助广大考生更好地备考,本文整理了10道2024年高压电工考试的最新解析及总结试题&a…...

OELOVE 6.0城市列表模板
研究了好久OELOVE6.0源码,一直想将城市列表给单独整出来,做地区排名,但是PHP程序都是加密的,非常难搞,做二开都是要命的处理不了,在这里有一个简单方法可以处理城市列表,并且可以自定义TDK&…...

如何将你的 Ruby 应用程序从 OpenSearch 迁移到 Elasticsearch
作者:来自 Elastic Fernando Briano 将 Ruby 代码库从 OpenSearch 客户端迁移到 Elasticsearch 客户端的指南。 OpenSearch Ruby 客户端是从 7.x 版 Elasticsearch Ruby 客户端分叉而来的,因此代码库相对相似。这意味着当将 Ruby 代码库从 OpenSearch 迁…...

day1数据结构,关键字,内存空间存储与动态分区,释放
小练习 在堆区空间连续申请5个int类型大小空间,用来存放从终端输入的5个学生成绩,然后显示5个学生成绩,再将学生成绩升序排序,排序后,再次显示学生成绩。显示和排序分别用函数完成(两种排序方法࿰…...
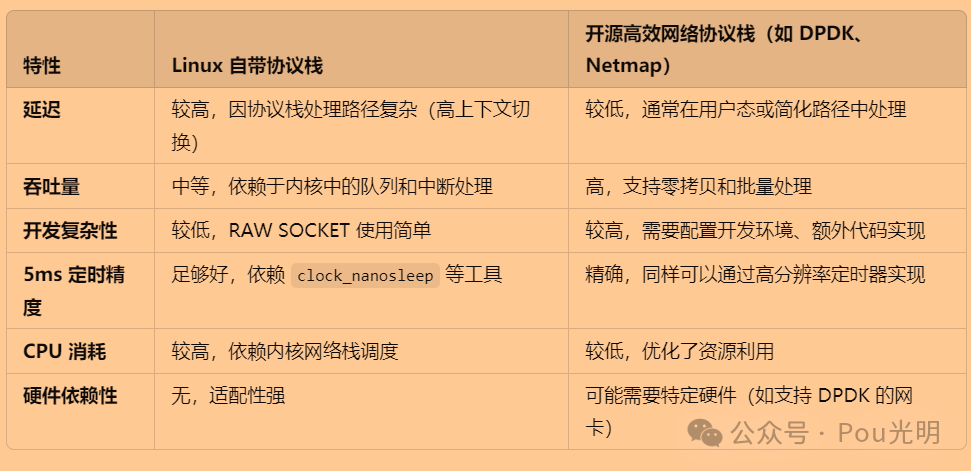
1_linux系统网络性能如何优化——几种开源网络协议栈比较
之前合集《计算机网络从入门到放弃》第一阶段算是已经完成了。都是理论,没有实操,让“程序猿”很难受,操作性不如 Modbus发送的报文何时等到应答和 tcp通信测试报告单1——connect和send。开始是想看linux内核网络协议栈的源码,然…...

【问题记录】07 MAC电脑,使用FileZilla(SFTP)连接堡垒机不成功
项目场景: 使用MAC电脑,以子账号(非root)的形式登录,连接堡垒机CLB(传统型负载均衡),使用FileZilla(SFTP)进行FTP文件传输。 问题描述: MAC电脑…...

前端报错npm ERR cb() never called问题
环境使用node版本v14.21.3,npm版本6.14.18 1.问题描述 1.1使用npm install后报错 npm ERR! cb() never called!npm ERR! This is an error with npm itself. Please report this error at: npm ERR! ? ? <https://npm.community>npm ERR! A complete log…...
康谋方案 | 多源相机数据采集与算法集成测试方案
目录 一、相机组成 二、多源相机采集与测试方案 三、应用案例分享 四、结语 在智能化技术快速发展当下,图像数据的采集与处理逐渐成为自动驾驶、工业等领域的一项关键技术。高质量的图像数据采集与算法集成测试都是确保系统性能和可靠性的关键。随着技术的不断进…...

Graspness 端到端抓取点估计 | 环境搭建 | 模型推理测试
在复杂场景中实现抓取检测,Graspness是一种端到端的方法; 输入点云数据,输出抓取角度、抓取深度、夹具宽度等信息。 开源地址:https://github.com/rhett-chen/graspness_implementation?tabreadme-ov-file 论文地址࿱…...
)
交换机是如何避免数据碰撞的(详细解释 + 示例)
交换机是如何避免数据碰撞的(详细解释 示例) 1. 独立冲突域 交换机的每个端口都形成一个独立的冲突域。这意味着通过交换机连接的每个设备都拥有自己的通信通道,互不干扰。 示例: 假设一个交换机有4个端口,分别连接…...

魅族手机刷官方系统
从魅族官网下载固件 https://flyme.cn/firmware.html 找到自己的型号,里面有历史版本、最新版,按照需求下载。 下载的是update.zip,改名就不能升级了 方法1 直接点击下载的update.zip包就可以升级。 方法2 将文件移动到文件管理的根目录&a…...

女人想要的,是那份懂她的情绪价值
女人想要的,是那份懂她的情绪价值 在情感的世界里,我们常常听到这样的声音:“我不需要你帮我解决问题,我只希望你能懂我。”这句话,简单却深刻,它揭示了女性在情感需求上的一个独特面向——她们渴望的&…...

[python SQLAlchemy数据库操作入门]-10.性能优化:提升 SQLAlchemy 在股票数据处理中的速度
哈喽,大家好,我是木头左! 当处理大量数据时,如股票数据,默认的ORM操作可能会显得效率低下。本文将探讨如何通过一些技巧和策略来优化SQLAlchemy ORM的性能,从而提升其在股票数据处理中的速度。 1. 选择合适的数据类型 在定义模型时,选择合适的数据类型对于性能至关重要…...

【网络取证篇】取证实战之PHP服务器镜像网站重构及绕密分析
【网络取证篇】取证实战之PHP服务器镜像网站重构及绕密分析 在裸聊敲诈、虚假理财诈骗案件类型中,犯罪分子为了能实现更低成本、更快部署应用的目的,其服务器架构多为常见的初始化网站架构,也称为站库同体服务器!也就是说网站应用…...

[python]使用 Pandas 处理 Excel 数据:分割与展开列操作
在数据处理的过程中,时常需要对 Excel 表格中的数据进行清洗与转换,下面介绍使用 Python 中的 Pandas 库对 Excel 文件中的数据进行操作,具体包括分割列、展开数据、清除空格以及格式转换等操作。 目标: 读取一个没有表头的 Exc…...

单片机的选择因素
在选择单片机型号时,需要根据具体的应用需求来选择合适的单片机。单片机(Microcontroller Unit, MCU)是一种将计算机的主要部分集成在一个芯片上的微型计算机,它通常包括处理器、存储器、输入/输出接口等。随着技术的发展…...

软件测试兼容性测试丨分布式测试与多设备管理
本文将从分布式测试的概念、重要性以及实施方法入手,紧接着探讨多设备管理的必要性和管理策略,最后分析其对软件测试行业的前景与影响。 分布式测试简介 什么是分布式测试? 分布式测试是指将测试任务分散到不同的计算机或者设备上进行&…...

XCTF-web-easyupload
试了试php,php7,pht,phtml等,都没有用 尝试.user.ini 抓包修改将.user.ini修改为jpg图片 在上传一个123.jpg 用蚁剑连接,得到flag...

【Oracle APEX开发小技巧12】
有如下需求: 有一个问题反馈页面,要实现在apex页面展示能直观看到反馈时间超过7天未处理的数据,方便管理员及时处理反馈。 我的方法:直接将逻辑写在SQL中,这样可以直接在页面展示 完整代码: SELECTSF.FE…...

python执行测试用例,allure报乱码且未成功生成报告
allure执行测试用例时显示乱码:‘allure’ �����ڲ����ⲿ���Ҳ���ǿ�&am…...

Unsafe Fileupload篇补充-木马的详细教程与木马分享(中国蚁剑方式)
在之前的皮卡丘靶场第九期Unsafe Fileupload篇中我们学习了木马的原理并且学了一个简单的木马文件 本期内容是为了更好的为大家解释木马(服务器方面的)的原理,连接,以及各种木马及连接工具的分享 文件木马:https://w…...

【 java 虚拟机知识 第一篇 】
目录 1.内存模型 1.1.JVM内存模型的介绍 1.2.堆和栈的区别 1.3.栈的存储细节 1.4.堆的部分 1.5.程序计数器的作用 1.6.方法区的内容 1.7.字符串池 1.8.引用类型 1.9.内存泄漏与内存溢出 1.10.会出现内存溢出的结构 1.内存模型 1.1.JVM内存模型的介绍 内存模型主要分…...

Cilium动手实验室: 精通之旅---13.Cilium LoadBalancer IPAM and L2 Service Announcement
Cilium动手实验室: 精通之旅---13.Cilium LoadBalancer IPAM and L2 Service Announcement 1. LAB环境2. L2公告策略2.1 部署Death Star2.2 访问服务2.3 部署L2公告策略2.4 服务宣告 3. 可视化 ARP 流量3.1 部署新服务3.2 准备可视化3.3 再次请求 4. 自动IPAM4.1 IPAM Pool4.2 …...

《Docker》架构
文章目录 架构模式单机架构应用数据分离架构应用服务器集群架构读写分离/主从分离架构冷热分离架构垂直分库架构微服务架构容器编排架构什么是容器,docker,镜像,k8s 架构模式 单机架构 单机架构其实就是应用服务器和单机服务器都部署在同一…...

五子棋测试用例
一.项目背景 1.1 项目简介 传统棋类文化的推广 五子棋是一种古老的棋类游戏,有着深厚的文化底蕴。通过将五子棋制作成网页游戏,可以让更多的人了解和接触到这一传统棋类文化。无论是国内还是国外的玩家,都可以通过网页五子棋感受到东方棋类…...

ubuntu22.04 安装docker 和docker-compose
首先你要确保没有docker环境或者使用命令删掉docker sudo apt-get remove docker docker-engine docker.io containerd runc安装docker 更新软件环境 sudo apt update sudo apt upgrade下载docker依赖和GPG 密钥 # 依赖 apt-get install ca-certificates curl gnupg lsb-rel…...

Visual Studio Code 扩展
Visual Studio Code 扩展 change-case 大小写转换EmmyLua for VSCode 调试插件Bookmarks 书签 change-case 大小写转换 https://marketplace.visualstudio.com/items?itemNamewmaurer.change-case 选中单词后,命令 changeCase.commands 可预览转换效果 EmmyLua…...
