12.11数据结构-图
无向完全图:在无向图中,如果任意两个顶点之间都存在边,则称该图为无向完全图。
有向完全图:在有向图中,如果任意两个顶点之间都存在方向相反的两条弧,则称该图为有向完全图。 
含有n个顶点的无向完全图有n×(n-1)/2条边。
含有n个顶点的有向完全图有n×(n-1)条边。
顶点的度:在无向图中,顶点v的度是指依附于
顶点的入度:在有向图中,顶点v的入度是指以该顶点为弧头的弧的数目,记为ID (v);
顶点的出度:在有向图中,顶点v的出度是指以该顶点为弧尾的弧的数目,记为OD (v)。
该顶点的边数,通常记为TD (v)。
在具有n个顶点、e条边的无向图G中,各顶点的度之和与边数之和的关系:

在具有n个顶点、e条边的有向图G中,各顶点的入度之和与各顶点的出度之和的关系?与边数之和的关系:

回路(环):第一个顶点和最后一个顶点相同的路径。
简单路径:序列中顶点不重复出现的路径。
简单回路(简单环):除了第一个顶点和最后一个顶点外,其余顶点不重复出现的回路。
子图:若图G=(V,E),G'=(V',E'),如果: V'ÍV 且E' Í E ,则称图G'是G的子图。

连通图:在无向图中,如果从一个顶点vi到另一个顶点vj(i≠j)有路径,则称顶点vi和vj是连通的。如果图中任意两个顶点都是连通的,则称该图是连通图。
连通分量:非连通图的极大连通子图称为连通分量。
一个n个顶点的连通无向图,其边的个数至少为( n-1 )
因为它如果是个树的话,边就最少了
连通(Connected)
-
无向图中的连通:在无向图中,如果任意两个顶点之间存在一条路径,那么这个图就是连通的。即从一个顶点出发,可以通过边访问到任何其他顶点。
-
有向图中的连通:在有向图中,如果从任意两个顶点中的一个可以通过有向边到达另一个,那么这两个顶点是连通的。但需要注意,这并不意味着整个图是连通的,仅是针对特定的顶点。
强连通(Strongly Connected)
-
有向图中的强连通:在有向图中,如果图中的每一对顶点 都能相互到达,那么这个图是强连通的。强连通要求顶点之间的路径是双向的。
-
对于无向图,强连通的概念并不适用,因为无向图的每条边本身就是双向的,通常直接称为“连通”。
总结
- 连通:在无向图中,任意两个顶点都有路径相连;在有向图中,特定的两个顶点之间有一条路径。
- 强连通:仅适用于有向图,表示任意两个顶点之间既可以从一个到达另一个,也可以从另一个到达前者。
要连通具有n个顶点的有向图,至少需要( n-1 )条边。
只要连通就行,不用强连通。所以画个单边的树就行

由握手定理知A正确,
在无向图中,握手定理表述为:所有顶点的度数之和等于边数的 2 倍。
通俗来讲,假如把图中的顶点看成是人,边看成是两个人握手,那么每个人握手的次数(即顶点的度数)加起来,就等于总的握手次数的 2 倍,因为每一条边(一次握手)会在两个顶点(两个人)的度数中各被计算一次。
BC错误,画个单边树,得到b错误,画个三角形得到c错误。
图的遍历
① 在图中,如何选取遍历的起始顶点?
在图中,任何两个顶点之间都可能存在边,顶点是没有确定的先后次序的,所以,顶点的编号不唯一。为了定义操作的方便,将图中的顶点按任意顺序排列起来,比如,按顶点的存储顺序。然后选取下标小的顶点
② 从某个起点始可能到达不了所有其它顶点,怎么办?
解决方案:多次调用从某顶点出发遍历图的算法。
③ 因图中可能存在回路,某些顶点可能会被重复访问,那么如何避免遍历不会因回路而陷入死循环?
解决方案:附设访问标志数组visited[n] 。
④ 在图中,一个顶点可以和其它多个顶点相连,当这样的顶点访问过后,如何选取下一个要访问的顶点?
解决方案:深度优先遍历和广度优先遍历。
邻接矩阵的DFS和BFS:
#include<iostream>
using namespace std;
int visited[10] = { 0 };class MGraph
{
public:MGraph(char a[], int n, int e);~MGraph() {};void DFS(int v);void BFS(int v);
private:char vertex[10];int edge[10][10];int vertexNum, edgeNum;};MGraph::MGraph(char a[], int n, int e)
{int i, j, k;vertexNum = n;edgeNum = e;for (i = 0; i < vertexNum; i++)vertex[i] = a[i];for (i = 0; i < vertexNum; i++)for (j = 0; j < vertexNum; j++)edge[i][j] = 0;for (k = 0; k < edgeNum; k++){cin >> i >> j;edge[i][j] = 1;edge[j][i] = 1;}
}void MGraph::DFS(int v)
{int j;cout << vertex[v];visited[v] = 1;for(j =0;j<vertexNum;j++)if (edge[v][j] == 1 && visited[j] == 0)DFS(j);
}void MGraph::BFS(int v)
{cout << vertex[v];visited[v] = 1;int w, j, Q[10];int front = -1, rear = -1;Q[++rear] = v;while (front != rear){w = Q[++front];for(j = 0;j<vertexNum;j++)if (edge[w][j] == 1 && visited[j] == 0){cout << vertex[j];visited[j] = 1;Q[++rear] = j;}}
}int main()
{int i;char ch[] = { 'A','B','C','D','E' };MGraph MG(ch, 5, 6);for (i = 0; i < 10; i++)visited[i] = 0;cout << "深搜:" << endl;MG.DFS(0);for (i = 0; i < 10; i++)visited[i] = 0;cout << endl;cout << "广搜" << endl;MG.BFS(0);
}邻接表:
#include<iostream>
using namespace std;
int visited[10] = { 0 };struct EdgeNode
{int adjvex;EdgeNode* next;
};struct VertexNode
{char vertex;EdgeNode* firstEdge;
};class ALGraph
{
public:ALGraph(char a[], int n, int e);~ALGraph() ;void DFS(int v);void BFS(int v);
private:VertexNode adjlist[10];int vertexNum, edgeNum;
};ALGraph::ALGraph(char a[], int n, int e)
{int i, j, k;EdgeNode* s = nullptr;vertexNum = n;edgeNum = e;for (i = 0; i < vertexNum; i++){adjlist[i].vertex = a[i];adjlist[i].firstEdge = nullptr;}for (k = 0; k < edgeNum; k++){cin >> i >> j;s = new EdgeNode;s->adjvex = j;s->next = adjlist[i].firstEdge;adjlist[i].firstEdge = s;}
}ALGraph::~ALGraph()
{EdgeNode* p = nullptr, * q = nullptr;for (int i = 0; i < vertexNum; i++){p = q = adjlist[i].firstEdge;while (p != nullptr){p = p->next;delete q;q = p;}}
}void ALGraph::DFS(int v)
{int j;EdgeNode* p = nullptr;cout << adjlist[v].vertex;visited[v] = 1;p = adjlist[v].firstEdge;while (p != nullptr){j = p->adjvex;if (visited[j] == 0)DFS(j);p = p->next;}
}void ALGraph::BFS(int v)
{int w, j, Q[10];int front = -1, rear = -1;EdgeNode* p = nullptr;cout << adjlist[v].vertex;visited[v] = 1;Q[++rear] = v;while (front != rear){w = Q[++front];p = adjlist[w].firstEdge;while (p != nullptr){j = p->adjvex;if (visited[j] == 0){cout << adjlist[j].vertex;visited[j] = 1;Q[++rear] = j;}p = p->next;}}
}int main()
{int i;char ch[] = { 'A','B','C','D','E' };ALGraph ALG(ch, 5, 6);ALG.DFS(0);for (i = 0; i < 10; i++)visited[i] = 0;cout << endl;ALG.BFS(0);
}相关文章:

12.11数据结构-图
无向完全图:在无向图中,如果任意两个顶点之间都存在边,则称该图为无向完全图。 有向完全图:在有向图中,如果任意两个顶点之间都存在方向相反的两条弧,则称该图为有向完全图。 含有n个顶点的无向完全图有…...

BERT模型入门(2)BERT的工作原理
文章目录 如名称所示,BERT(来自Transformer的双向编码器表示)是基于Transformer模型。我们可以将BERT视为只有编码器部分的Transformer。 在上一个主题《Transformer入门》中,我们了解到将句子作为输入喂给Transformer的编码器&a…...

python3 中的成员运算符
一. 简介 在Python 3中,成员运算符用于测试序列(如字符串、列表、元组、集合或字典)中是否包含某个值。身份运算符用于比较两个对象的身份,即它们是否引用内存中的同一个对象。 本文简单学习一下 python3 中的成员运算符与身份运…...

【测试面试篇1】测试开发与开发|selenium实现自动化测试|设计测试用例|常见的测试方法|开发不认可提测试的bug该怎么办
目录 1.选择走测试为什么还要学这么多的开发知识? 2.为什么选择软件测试开发岗位而不是软件开发岗位? 3.个人的职业规划是什么? 4.测试中遇到的问题如何进行解决? 5.对自己的项目做过哪些测试工作? 6.描述selenium…...

人大金仓数据linux安装注意事项
人大金仓数据linux安装注意事项 本次是个人搭建虚拟机安装centos7的环境下进行安装。 1、安装流程参照https://help.kingbase.com.cn/v9/install-updata/install-linux/preface.html。 2、mount安装文件报错 操作手册提供mount的命令如下: mount KingbaseES_V009R0…...

【Maven】多模块项目的构建
项目构建 什么是构建? 项目构建指的是将源代码和资源文件转换为可执行或可分发的软件制品(如 JAR、WAR 文件)的过程。这个过程不仅包括编译代码,还包括运行测试、打包、部署等步骤。Maven 提供了一套标准化的方法来处理这些任务…...

大模型学习笔记------SAM模型详解与思考
大模型学习笔记------SAM模型详解与思考 1、SAM框架概述2、Segment Anything Task3、Segment Anything Model SAM模型是Meta 提出的分割一切模型(Segment Anything Model,SAM)突破了分割界限,极大地促进了计算机视觉基础模型的发展…...

crictl和ctr与docker的命令的对比
crictl是遵循CRI接口规范的一个命令行工具,通常用它来检查和管理kubelet节点上的容器运行时和镜像 ctr是containerd的一个客户端工具, 接下来就是crictl的的常见命令,其中能完全替代docker命令的参照下列表格 操作crictldocker查看运行容器…...
)
SQLite建表语句示例(含所有数据类型、索引、自增主键、唯一索引)
下面是一个示例,展示如何创建一个用户信息表。 包含 SQLite 支持的所有数据类型,同时设置主键为自增、一个字段为唯一索引,以及另一个字段为普通索引: -- 创建用户信息表 CREATE TABLE user_info (id INTEGER PRIMARY KEY AUTOI…...

探秘Redis哨兵模式:原理、运行与风险全解析
一、引言 Redis 概述 在当今的数据存储领域,Redis 占据着十分重要的地位。它是一个内存中的数据存储,凭借其出色的性能和丰富的功能,被数百万开发人员广泛应用于诸多场景之中,已然成为构建高性能、可扩展应用程序的得力工具。 从…...
.NET平台使用C#设置Excel单元格数值格式
设置Excel单元格的数字格式是创建、修改和格式化Excel文档的关键步骤之一,它不仅确保了数据的正确表示,还能够增强数据的可读性和专业性。正确的数字格式可以帮助用户更直观地理解数值的意义,减少误解,并且对于自动化报告生成、财…...

零基础学安全--wireshark简介
目录 主要功能 捕获网络数据包 协议解析 数据包分析 数据包重组 过滤功能 统计与图表功能 官网 Wireshark是一个开源的网络协议分析工具 主要功能 捕获网络数据包 能够实时捕获网络中传输的数据包,用户选择要监听的网络接口(如以太网、WiFi等…...

[Flutter] : Clipboard
import package:flutter/material.dart; import package:flutter/services.dart; setData Clipboard.setData(ClipboardData(text: "传入的文字内容")); getData Clipboard.getData(Clipboard.kTextPlain) 记录 | Flutter剪切板-刨根问底做一个可以在后台…...
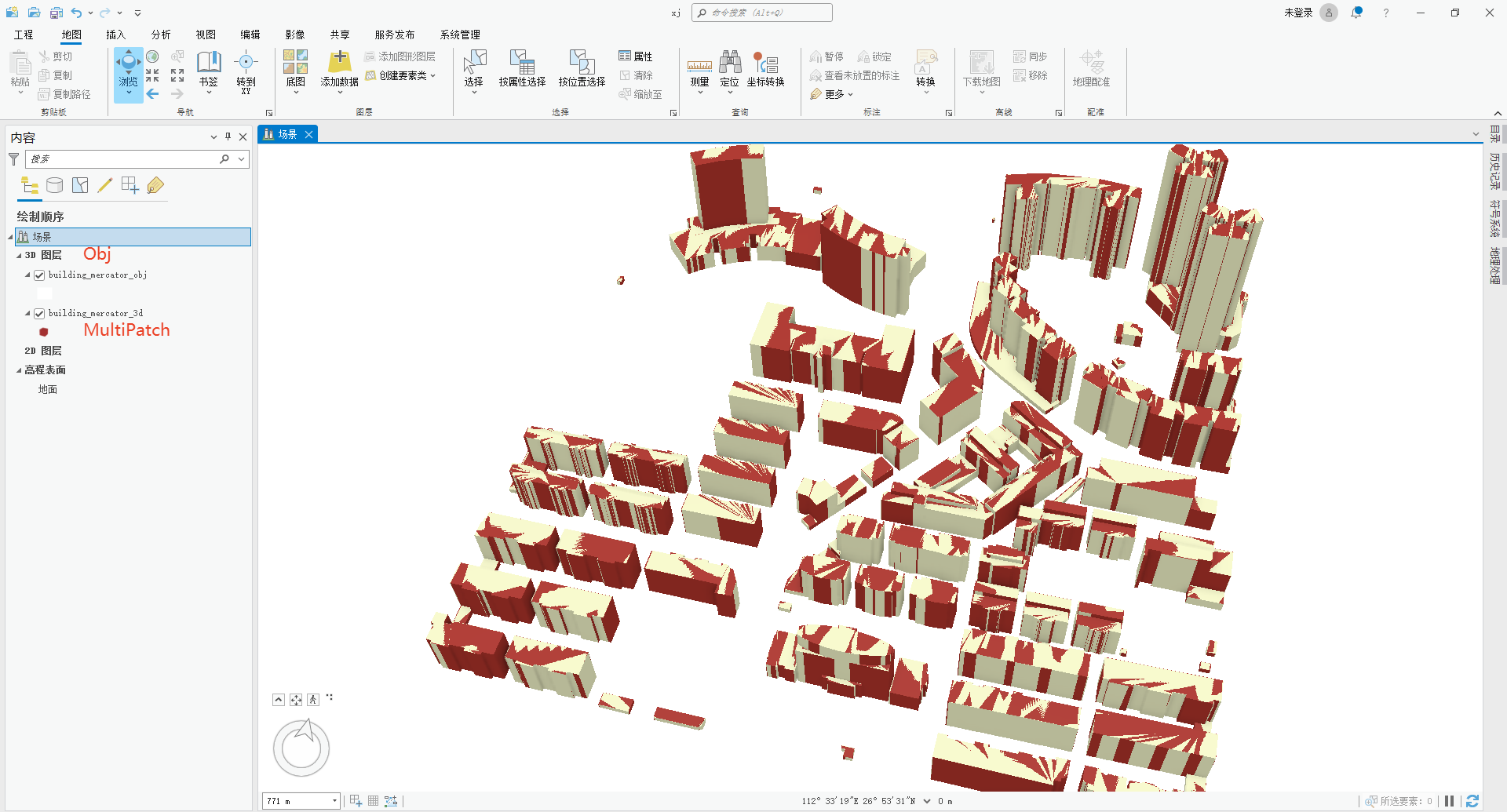
ArcGIS MultiPatch数据转换Obj数据
文章目录 ArcGIS MultiPatch数据转换Obj数据1 效果2 技术路线2.1 Multipatch To Collada2.2 Collada To Obj3 代码实现4 附录4.1 环境4.2 一些坑ArcGIS MultiPatch数据转换Obj数据 1 效果 2 技术路线 MultiPatch --MultipatchToCollada–> Collada --Assimp–> Obj 2.…...

《开源数据:开启信息共享与创新的宝藏之门》
《开源数据:开启信息共享与创新的宝藏之门》 一、开源数据概述(一)开源数据的定义(二)开源数据的发展历程 二、开源数据的优势(一)成本效益优势(二)灵活性与可定制性&…...

如何评估基于TRIZ理论生成的方案的可行性和有效性?
在科技创新与问题解决的过程中,TRIZ理论(发明问题解决理论)以其系统性和高效性著称,为工程师和创新者提供了一套强大的工具和方法。然而,仅仅依靠TRIZ理论生成创新方案并不足以确保项目的成功,关键在于如何…...

sh-寡肽-78——头发护理多肽原料,改善头发外观
主要特征 人的头发纤维结构由角质层、皮质和髓质组成。角质层约占头发重量的 15%,由重叠的细胞层组成,类似于鳞片系统,半胱氨酸含量很高。它为头发纤维提供保护作用。皮质是头发的中间区域,负责头发的强度、弹性和颜色。它由多种细…...

metagpt 多智能体系统
metagpt 多智能体系统 代码1. 动作及角色定义2. 主函数 代码解释1. 导入模块:2. 环境设置:3. 定义行动(Action):4. 定义角色(Role):5. 学生和老师的行为:6. 主函数&#…...

下采样在点云处理中的关键作用——以PointNet++为例【初学者无门槛理解版!】
一、前言 随着3D传感器技术的快速发展,点云数据在计算机视觉、机器人导航、自动驾驶等领域中的应用日益广泛。点云作为一种高效的3D数据表示方式,能够精确地描述物体的几何形状和空间分布。然而,点云数据通常具有高维度和稀疏性的特点&#…...
函数)
pytorch ---- torch.linalg.norm()函数
torch.linalg.norm 是 PyTorch 中用于计算张量范数(Norm)的函数。范数是线性代数中的一个重要概念,用于量化向量或矩阵的大小或长度。这个函数可以处理任意形状的张量,支持多种类型的范数计算。 1.函数签名 torch.linalg.norm(…...
)
Java 语言特性(面试系列1)
一、面向对象编程 1. 封装(Encapsulation) 定义:将数据(属性)和操作数据的方法绑定在一起,通过访问控制符(private、protected、public)隐藏内部实现细节。示例: public …...

23-Oracle 23 ai 区块链表(Blockchain Table)
小伙伴有没有在金融强合规的领域中遇见,必须要保持数据不可变,管理员都无法修改和留痕的要求。比如医疗的电子病历中,影像检查检验结果不可篡改行的,药品追溯过程中数据只可插入无法删除的特性需求;登录日志、修改日志…...

《从零掌握MIPI CSI-2: 协议精解与FPGA摄像头开发实战》-- CSI-2 协议详细解析 (一)
CSI-2 协议详细解析 (一) 1. CSI-2层定义(CSI-2 Layer Definitions) 分层结构 :CSI-2协议分为6层: 物理层(PHY Layer) : 定义电气特性、时钟机制和传输介质(导线&#…...

ElasticSearch搜索引擎之倒排索引及其底层算法
文章目录 一、搜索引擎1、什么是搜索引擎?2、搜索引擎的分类3、常用的搜索引擎4、搜索引擎的特点二、倒排索引1、简介2、为什么倒排索引不用B+树1.创建时间长,文件大。2.其次,树深,IO次数可怕。3.索引可能会失效。4.精准度差。三. 倒排索引四、算法1、Term Index的算法2、 …...

IT供电系统绝缘监测及故障定位解决方案
随着新能源的快速发展,光伏电站、储能系统及充电设备已广泛应用于现代能源网络。在光伏领域,IT供电系统凭借其持续供电性好、安全性高等优势成为光伏首选,但在长期运行中,例如老化、潮湿、隐裂、机械损伤等问题会影响光伏板绝缘层…...

C/C++ 中附加包含目录、附加库目录与附加依赖项详解
在 C/C 编程的编译和链接过程中,附加包含目录、附加库目录和附加依赖项是三个至关重要的设置,它们相互配合,确保程序能够正确引用外部资源并顺利构建。虽然在学习过程中,这些概念容易让人混淆,但深入理解它们的作用和联…...

虚拟电厂发展三大趋势:市场化、技术主导、车网互联
市场化:从政策驱动到多元盈利 政策全面赋能 2025年4月,国家发改委、能源局发布《关于加快推进虚拟电厂发展的指导意见》,首次明确虚拟电厂为“独立市场主体”,提出硬性目标:2027年全国调节能力≥2000万千瓦࿰…...

C++ 设计模式 《小明的奶茶加料风波》
👨🎓 模式名称:装饰器模式(Decorator Pattern) 👦 小明最近上线了校园奶茶配送功能,业务火爆,大家都在加料: 有的同学要加波霸 🟤,有的要加椰果…...
与文本切分器(Splitter)详解《二》)
LangChain 中的文档加载器(Loader)与文本切分器(Splitter)详解《二》
🧠 LangChain 中 TextSplitter 的使用详解:从基础到进阶(附代码) 一、前言 在处理大规模文本数据时,特别是在构建知识库或进行大模型训练与推理时,文本切分(Text Splitting) 是一个…...

STM32标准库-ADC数模转换器
文章目录 一、ADC1.1简介1. 2逐次逼近型ADC1.3ADC框图1.4ADC基本结构1.4.1 信号 “上车点”:输入模块(GPIO、温度、V_REFINT)1.4.2 信号 “调度站”:多路开关1.4.3 信号 “加工厂”:ADC 转换器(规则组 注入…...
