pytorch ---- torch.linalg.norm()函数
torch.linalg.norm 是 PyTorch 中用于计算张量范数(Norm)的函数。范数是线性代数中的一个重要概念,用于量化向量或矩阵的大小或长度。这个函数可以处理任意形状的张量,支持多种类型的范数计算。
1.函数签名
torch.linalg.norm(input, ord=None, dim=None, keepdim=False, dtype=None) -> Tensor
参数说明
-
input:
要计算范数的张量。 -
ord(可选):
范数的类型,决定范数的计算公式。常见值:None(默认):计算 Frobenius 范数(矩阵)或 2 范数(向量)。1: 1 范数(列绝对值之和,或向量绝对值之和)。2: 2 范数(Euclidean 范数,平方和的平方根)。'fro': Frobenius 范数(矩阵的元素平方和开方)。inf: 无穷范数(矩阵的行绝对值和最大值)。-inf: 负无穷范数(矩阵的行绝对值和最小值)。
-
dim(可选):
指定计算范数的维度。- 若为
None,计算整个张量的范数。 - 若指定为单个或多个维度,则按维度计算范数。
- 若为
-
keepdim(布尔,可选):
如果为True,结果会保留被归约的维度,维度的大小为1。 -
dtype(可选):
指定计算中使用的数据类型,常用于提高数值精度。
返回值
返回计算出的张量范数。结果是一个标量或一个张量(取决于是否指定 dim 参数)。
常见用法示例
(1) 计算向量的 2 范数
计算向量的欧几里得长度(平方和的平方根)。
import torchx = torch.tensor([3.0, 4.0])
norm = torch.linalg.norm(x)
print(norm) # 输出: 5.0 (因为 sqrt(3^2 + 4^2) = 5)
(2) 计算矩阵的 Frobenius 范数
A = torch.tensor([[1.0, 2.0], [3.0, 4.0]])
norm = torch.linalg.norm(A, ord='fro')
print(norm) # 输出: 5.4772 (因为 sqrt(1^2 + 2^2 + 3^2 + 4^2) ≈ 5.4772)
(3) 按维度计算范数
B = torch.tensor([[1.0, 2.0], [3.0, 4.0]])
norm_dim0 = torch.linalg.norm(B, ord=1, dim=0)
print(norm_dim0) # 输出: tensor([4., 6.]) (列绝对值之和)norm_dim1 = torch.linalg.norm(B, ord=1, dim=1)
print(norm_dim1) # 输出: tensor([3., 7.]) (行绝对值之和)
(4) 计算无穷范数
C = torch.tensor([[1.0, -2.0], [3.0, -4.0]])
inf_norm = torch.linalg.norm(C, ord=float('inf'))
print(inf_norm) # 输出: 7.0 (最大行绝对值和)
(5) 计算负无穷范数
neg_inf_norm = torch.linalg.norm(C, ord=float('-inf'))
print(neg_inf_norm) # 输出: 3.0 (最小行绝对值和)
相关文章:
函数)
pytorch ---- torch.linalg.norm()函数
torch.linalg.norm 是 PyTorch 中用于计算张量范数(Norm)的函数。范数是线性代数中的一个重要概念,用于量化向量或矩阵的大小或长度。这个函数可以处理任意形状的张量,支持多种类型的范数计算。 1.函数签名 torch.linalg.norm(…...

系列1:基于Centos-8.6部署Kubernetes (1.24-1.30)
每日禅语 “木末芙蓉花,山中发红萼,涧户寂无人,纷纷开自落。”这是王维的一首诗,名叫《辛夷坞》。这首诗写的是在辛夷坞这个幽深的山谷里,辛夷花自开自落,平淡得很,既没有生的喜悦ÿ…...
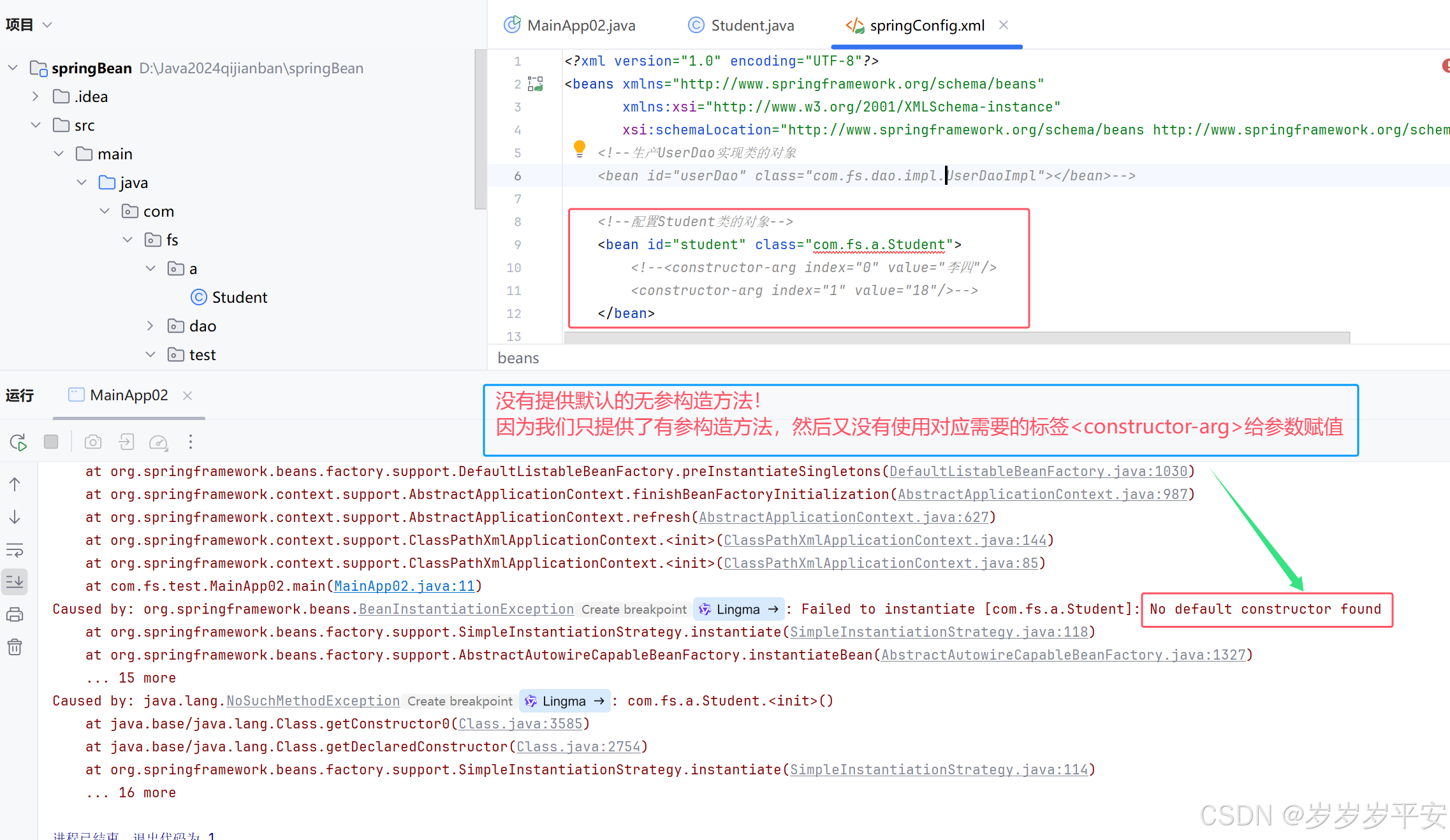
spring学习(spring-bean实例化(无参构造与有参构造方法实现)详解)
目录 一、spring容器之bean的实例化。 (1)"bean"基本概念。 (2)spring-bean实例化的几种方式。 二、spring容器使用"构造方法"的方式实例化bean。 (1)无参构造方法实例化bean。 &#…...
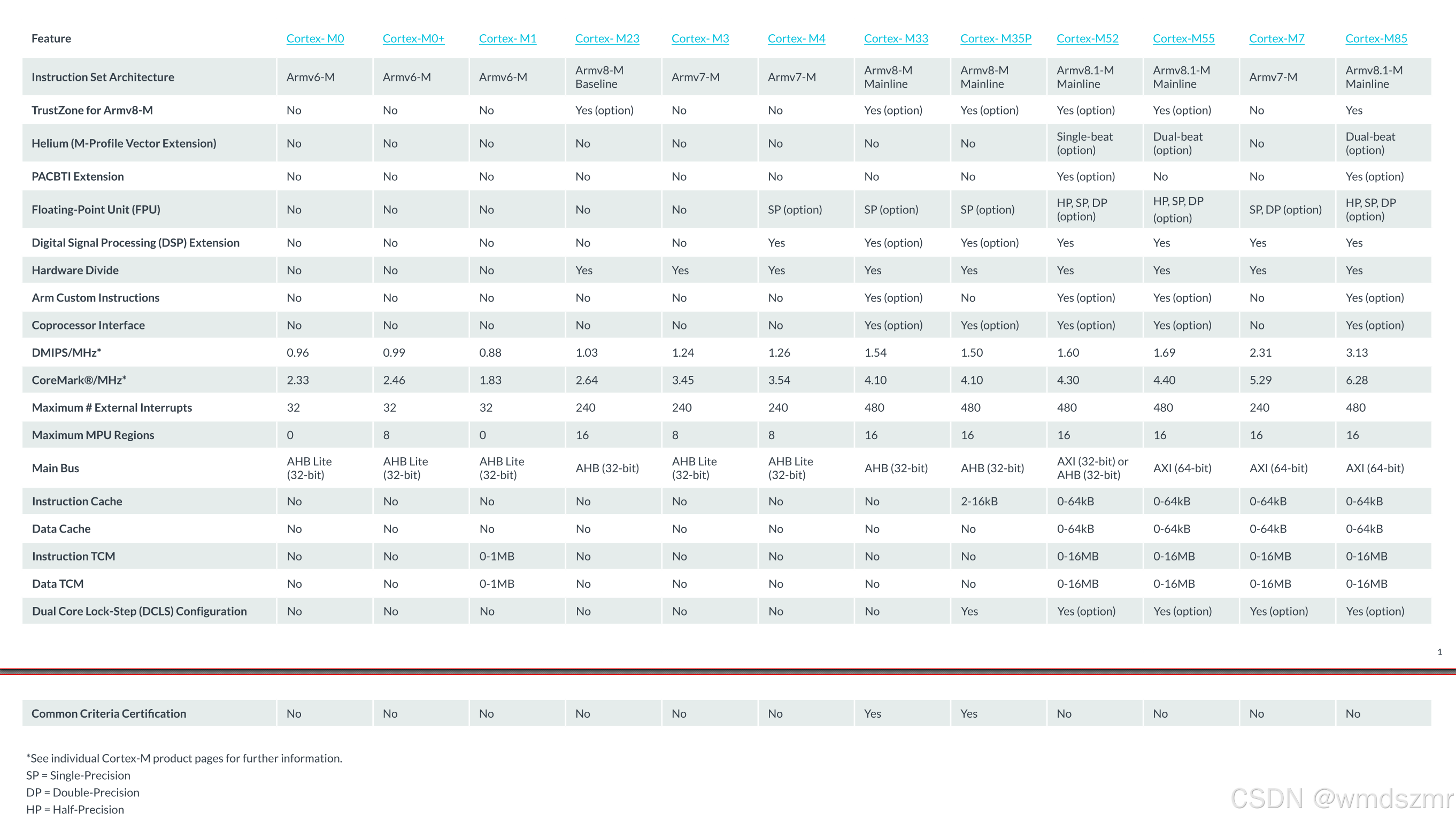
Arm Cortex-M处理器对比表
Arm Cortex-M处理器对比表 当前MCU处理器上主要流行RISC-V和ARM处理器,其他的内核相对比较少;在这两种内核中,又以Arm Cortex-M生态环境相对健全,大部分的厂家都在使用ARM的处理器。本文主要介绍Arm Cortex-M各个不同系列的参数对…...
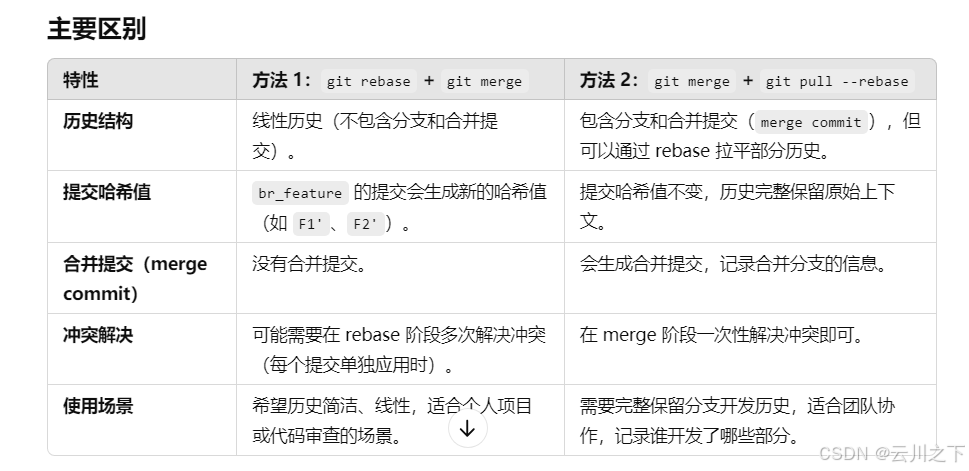
【git、gerrit】特性分支合入主分支方法 git rebase 、git cherry-pick、git merge
文章目录 1. 场景描述1.1 分支状态 2. 推荐的操作方式方法 1:git merge(保留分支结构)方法 2:git rebase(线性合并提交历史)直接在master分支执行git merge br_feature,再 执行 git pull --reba…...

WPF 相比 winform 的优势
wpf 相比 winform 的一些优点,网上也是众说纷纭,总的来说包括下面几点: 丰富的视觉效果:能够创建更具吸引力和现代化的用户界面,支持更复杂的图形和动画效果。不需要像 winform 一样,稍微做一点效果&#x…...
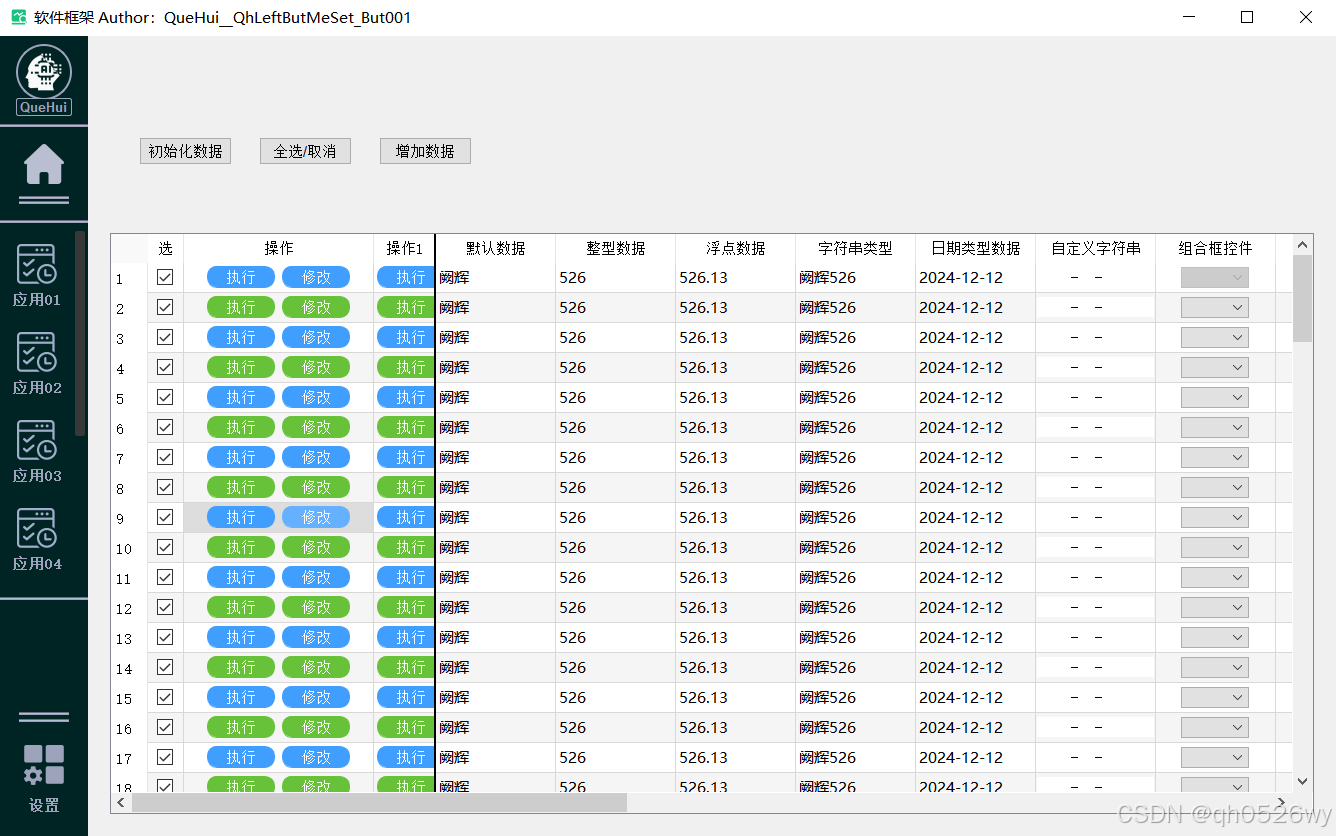
PYQT5程序框架
pyqt5程序框架_哔哩哔哩_bilibili 1.UI代码 Qhkuja.py # -*- coding: utf-8 -*-# Form implementation generated from reading ui file Qhkuja.ui # # Created by: PyQt5 UI code generator 5.15.7 # # WARNING: Any manual changes made to this file will be lost when py…...

Linux 中的 mkdir 命令:深入解析
在 Linux 系统中,mkdir 命令用于创建目录。它是文件系统管理中最基础的命令之一,广泛应用于日常操作和系统管理中。本文将深入探讨 mkdir 命令的功能、使用场景、高级技巧,并结合 GNU Coreutils 的源码进行详细分析。 1. mkdir 命令的基本用法…...

【人工智能解读】神经网络(CNN)的特点及其应用场景器学习(Machine Learning, ML)的基本概念
前些天发现了一个巨牛的人工智能学习网站,通俗易懂,风趣幽默, 忍不住分享一下给大家。点击跳转到网站 学习总结 1、掌握 JAVA入门到进阶知识(持续写作中……) 2、学会Oracle数据库入门到入土用法(创作中……) 3、手把…...
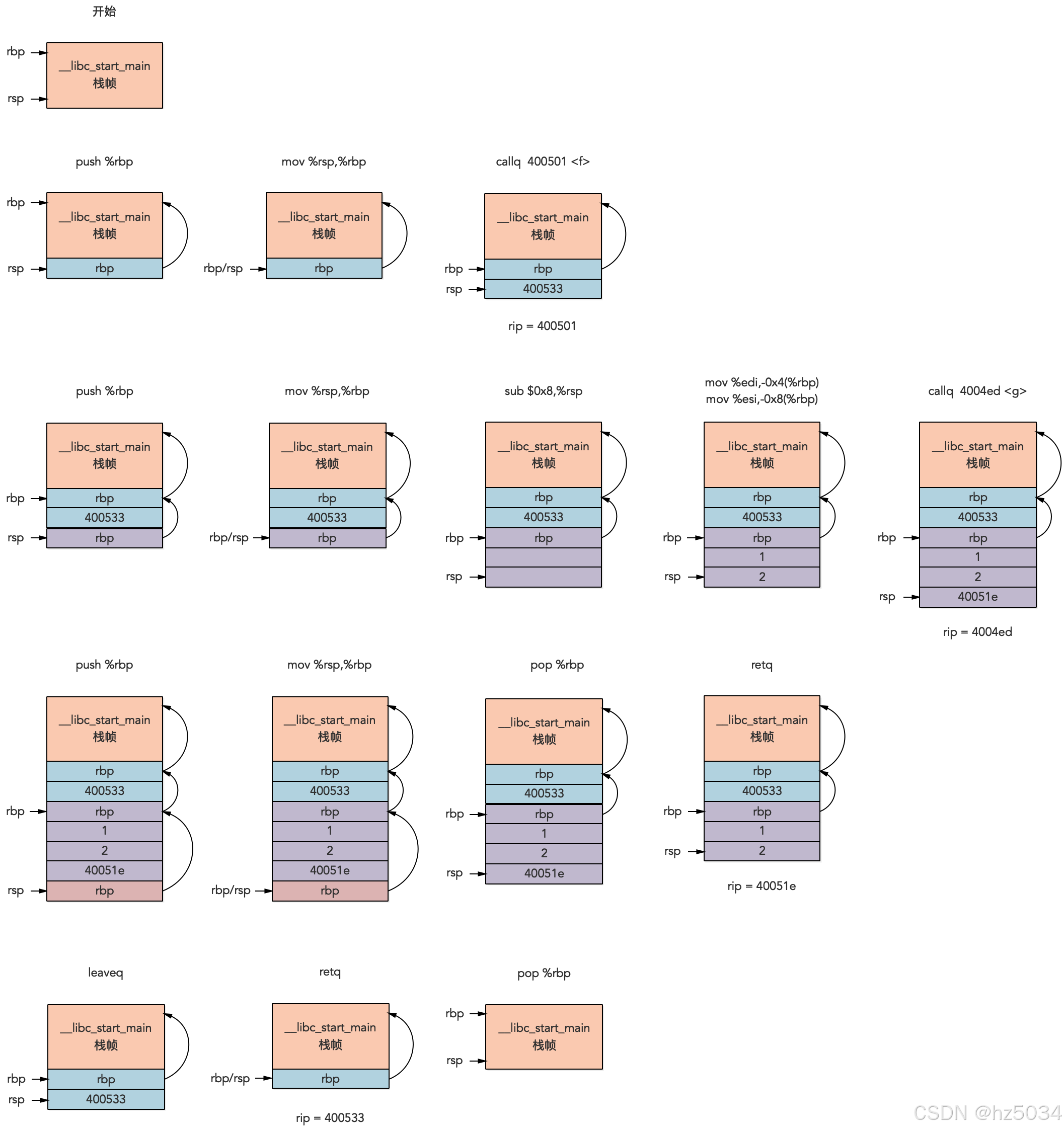
Linux栈帧
相关寄存器&指令 寄存器 rax(accumulator):return value rbx(base) rcx(count):4st argument rdx(data):3st argument rsi(sour…...
)
leetcode刷题——回溯算法(1)
目录 77题. 组合 216.组合总和III 17.电话号码的字母组合 39. 组合总和 40.组合总和II 131.分割回文串 93.复原IP地址 78.子集 90.子集II 491.非递减子序列 46.全排列 47.全排列 II 332.重新安排行程 51. N皇后 37. 解数独 回溯的本质是穷举,穷举所有…...

3D相框案例讲解(详细)
前言 通过现阶段的学习,我们已经掌握了HTML,CSS和JS部分的相关知识点,现在让我们通过一篇案例,来巩固我们近期所学的知识点。 详细视频讲解戳这里 任务一 了解目标案例样式 1.1了解案例 3D相框 1.2 分析案例 首先我们看到一个…...

制作安装包
使用打包工具(如 NSIS、Inno Setup、Advanced Installer)制作安装包。 示例:Inno Setup 制作安装包 Inno Setup Inno Setup 是一个免费且强大的安装包制作工具,可以用来打包 Qt 项目或其他软件程序。以下是使用 Inno Setup 制作…...
P8615 拼接平方数 P8699 排列数
文章目录 [蓝桥杯 2014 国 C] 拼接平方数[蓝桥杯 2019 国 B] 排列数 [蓝桥杯 2014 国 C] 拼接平方数 题目描述 小明发现 49 49 49 很有趣,首先,它是个平方数。它可以拆分为 4 4 4 和 9 9 9,拆分出来的部分也是平方数。 169 169 169 也有…...
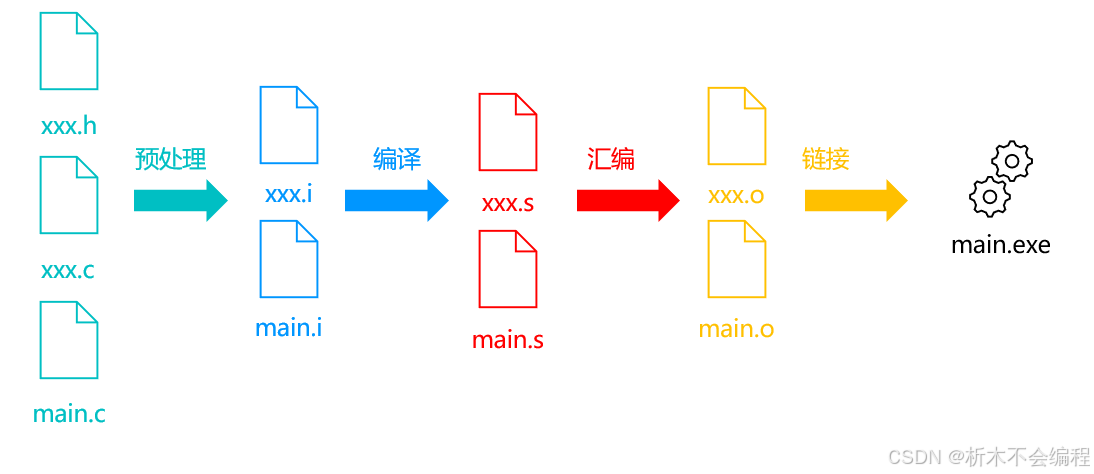
【C语言】拆解C语言的编译过程
前言 学习C语言的过程中,涉及到各种各样的关键词,在我们点击编译的时候,都会做什么呢?让我们来拆解一下 C语言的编译过程 C语言的编译过程包括预处理、编译、汇编和链接四个主要步骤。每个步骤都有其特定的任务和输出文件类型&am…...

【C++】青蛙跳跃问题解析与解法
博客主页: [小ᶻ☡꙳ᵃⁱᵍᶜ꙳] 本文专栏: C 文章目录 💯前言💯题目描述第一部分:基本青蛙过河问题第二部分:石柱和荷叶问题 💯解题思路与分析第一部分:青蛙过河问题解法思路:递…...

自动驾驶AVM环视算法--python版本的俯视TOP投影模式
c语言版本和算法原理的可以查看本人的其他文档。《自动驾驶AVM环视算法--全景的俯视图像和原图》本文档进用于展示部分代码的视线,获取方式网盘自行获取(非免费介意勿下载):链接: https://pan.baidu.com/s/1MJa8ZCEfNyLc5x0uVegto…...

Go 语言与时间拳击理论下的结对编程:开启高效研发编程之旅
一、引言 结对编程作为一种软件开发方法,在提高代码质量、增强团队协作等方面具有显著优势。而时间拳击理论为结对编程带来了新的思考角度。本文将以 Go 语言为中心,深入探讨时间拳击理论下的结对编程。 在当今软件开发领域,高效的开发方法和…...
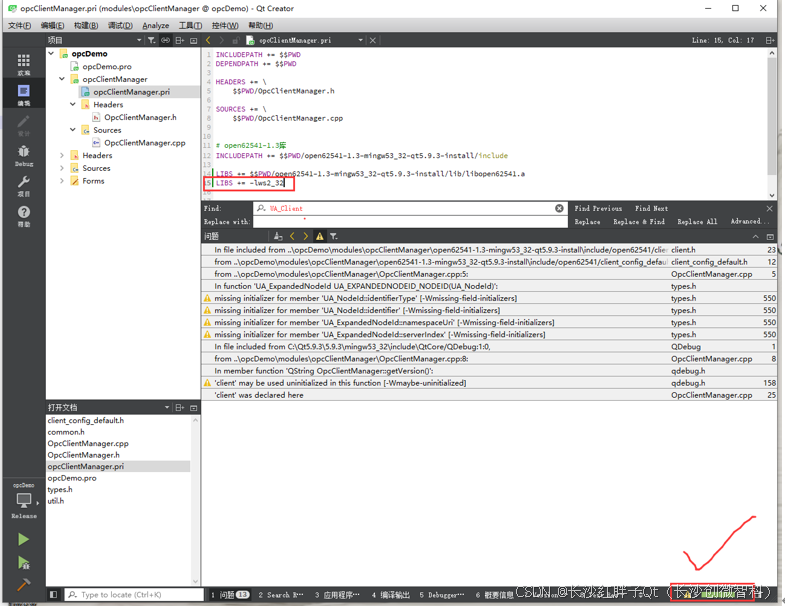
Qt+OPC开发笔记(一):OPCUA介绍、open62541介绍、编译与基础环境Demo
若该文为原创文章,转载请注明原文出处 本文章博客地址:https://hpzwl.blog.csdn.net/article/details/144516882 长沙红胖子Qt(长沙创微智科)博文大全:开发技术集合(包含Qt实用技术、树莓派、三维、OpenCV…...
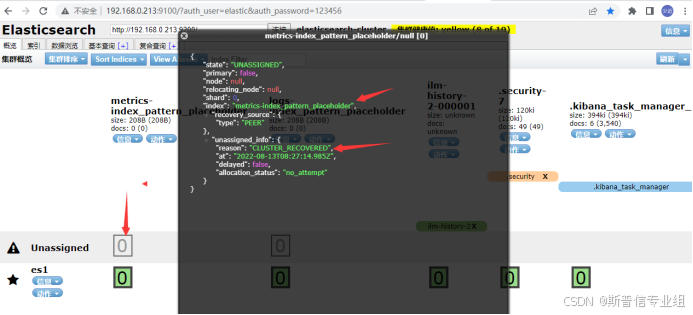
ElasticSearch 常见故障解析与修复秘籍
文章目录 一、ElasticSearch启动服务提示无法使用root用户二、ElasticSearch启动提示进程可拥有的虚拟内存少三、ElasticSearch提示用户拥有的可创建文件描述符太少四、ElasticSearch集群yellow状态分析五、ElasticSearch节点磁盘使用率过高,read_only状态问题解决六…...

未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?
编辑:陈萍萍的公主一点人工一点智能 未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?RWM通过双自回归机制有效解决了复合误差、部分可观测性和随机动力学等关键挑战,在不依赖领域特定归纳偏见的条件下实现了卓越的预测准…...
)
Java 语言特性(面试系列1)
一、面向对象编程 1. 封装(Encapsulation) 定义:将数据(属性)和操作数据的方法绑定在一起,通过访问控制符(private、protected、public)隐藏内部实现细节。示例: public …...
使用rpicam-app通过网络流式传输视频)
树莓派超全系列教程文档--(62)使用rpicam-app通过网络流式传输视频
使用rpicam-app通过网络流式传输视频 使用 rpicam-app 通过网络流式传输视频UDPTCPRTSPlibavGStreamerRTPlibcamerasrc GStreamer 元素 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 使用 rpicam-app 通过网络流式传输视频 本节介绍来自 rpica…...

FFmpeg 低延迟同屏方案
引言 在实时互动需求激增的当下,无论是在线教育中的师生同屏演示、远程办公的屏幕共享协作,还是游戏直播的画面实时传输,低延迟同屏已成为保障用户体验的核心指标。FFmpeg 作为一款功能强大的多媒体框架,凭借其灵活的编解码、数据…...

VTK如何让部分单位不可见
最近遇到一个需求,需要让一个vtkDataSet中的部分单元不可见,查阅了一些资料大概有以下几种方式 1.通过颜色映射表来进行,是最正规的做法 vtkNew<vtkLookupTable> lut; //值为0不显示,主要是最后一个参数,透明度…...

EtherNet/IP转DeviceNet协议网关详解
一,设备主要功能 疆鸿智能JH-DVN-EIP本产品是自主研发的一款EtherNet/IP从站功能的通讯网关。该产品主要功能是连接DeviceNet总线和EtherNet/IP网络,本网关连接到EtherNet/IP总线中做为从站使用,连接到DeviceNet总线中做为从站使用。 在自动…...

【JavaWeb】Docker项目部署
引言 之前学习了Linux操作系统的常见命令,在Linux上安装软件,以及如何在Linux上部署一个单体项目,大多数同学都会有相同的感受,那就是麻烦。 核心体现在三点: 命令太多了,记不住 软件安装包名字复杂&…...

云原生玩法三问:构建自定义开发环境
云原生玩法三问:构建自定义开发环境 引言 临时运维一个古董项目,无文档,无环境,无交接人,俗称三无。 运行设备的环境老,本地环境版本高,ssh不过去。正好最近对 腾讯出品的云原生 cnb 感兴趣&…...

算法:模拟
1.替换所有的问号 1576. 替换所有的问号 - 力扣(LeetCode) 遍历字符串:通过外层循环逐一检查每个字符。遇到 ? 时处理: 内层循环遍历小写字母(a 到 z)。对每个字母检查是否满足: 与…...
实现跳一跳小游戏)
鸿蒙(HarmonyOS5)实现跳一跳小游戏
下面我将介绍如何使用鸿蒙的ArkUI框架,实现一个简单的跳一跳小游戏。 1. 项目结构 src/main/ets/ ├── MainAbility │ ├── pages │ │ ├── Index.ets // 主页面 │ │ └── GamePage.ets // 游戏页面 │ └── model │ …...
