Emacs 折腾日记(五)——elisp 数字类型
本文是参考 emacs lisp 简明教程 写的,很多东西都是照搬里面的内容,如果各位读者觉得本文没有这篇教程优秀或者有抄袭嫌疑、又或者觉得我更新比较慢、再或者其他什么原因,请直接阅读上述链接中的教程。
上一篇我们讲了elisp中的流程控制结构相关的内容,下面就该进入到对应数据结构的学习了。elisp中主要的数据结构有:整数、浮点数、列表、符号、向量、散列表等等类型。下面我们先从最简单的类型——整数和浮点数说起
数字类型
与C/C++对比起来,elisp数字类型少的多,C/C++ 整数类型就有好几种,包括有符号、无符号、int、short、long之类的。elisp不区分这些,它仅仅有整数和浮点数。而且elisp 中只有浮点数这一种小数类型,不像C/C++还有双精度浮点数和单精度浮点数之分。
elisp的整数范围与具体的机器有关,它的范围可以通过变量 most-positive-fixnum 和 most-negative-fixnum 来得到。例如在我的机器上它们的值如下
most-positive-fixnum ;; 2305843009213693951
most-negative-fixnum ;; -2305843009213693952
在给变量使用数字类型赋值的时候,我们可以使用10进制或者其他任意进制的形式。例如
#b101100 => 44 ; 二进制
#o54 => 44 ; 八进制
#x2c => 44 ; 十进制
#24r1k => 44 ; 二十四进制
因为26个英文字母+10个数字的原因,我们最大只能使用36进制来表示一个数字,但是基本不用到这么大的。日常最多也就用用10进制、二进制、16进制、8进制都算用的少。
浮点数的表达遵循 IEEE 标准,也就是可以使用带小数点的数字来表示,或者带上 e 来使用科学计数法,例如
3.14
1.0e-10
数字类型的测试
作为动态类型的语言,在代码执行阶段,变量的类型是会发生变化的。我们无法仅通过变量名或者变量的初始化值来判断变量类型。emacs的变量在执行阶段都知道自己的类型,但是它无法主动向我们报告,我们需要使用一些函数来进行判断,关于数字类型,提供了下列的函数
integerp
floatp
numberp
从字面上能理解它们分别判断是否是整形、浮点数、以及数字类型。
elisp 测试函数一般都是用 p 来结尾,p 是 predicate 的第一个字母。如果函数名是一个单词,通常只是在这个单词后加一个 p,如果是多个单词,一般是加 -p
数的比较
与C/C++ 类似,数字的比较一般有 >、<、>=、<= 。但是也有不同的地方,因为elisp中都是使用 setq 来进行赋值的,所以它采用 = 来表示数学意义上的相等。还有一个不同的地方因为elisp中没有 += 、-=、/= 、*= 这样的运算符,所以它使用 /= 来作为不等的判断符号
与其他语言类似的,浮点数直接使用等于或者不等于来判断并不准确,需要在一定范围内忽略误差。在C/C++中,我们常见的写法是给定一个误差值,然后二者差的绝对值在这个误差值范围内则认为它们相等。我们将这个算法使用elisp改写一下就得到下面的代码
(defun approx-equal (x y)(let ((fuzz-factor 1.0e-6))(< (abs (- x y)) fuzz-factor)))(approx-equal 1.000001 1.00000000000000001) ;; => t
上述的写法并不严谨,在一定误差范围内,它是对的,但是在某些情况下它就不对了,例如 1.0e-7 和 1.0e-12 。它们本身并不相等,但是它们都超过了这个误差范围,相减之后的值小于这个误差范围。但是我们看到其实它们直接的差距还是挺大的,间隔1.0e5 的数量积。我们可以将上述算法进行一些改进
(defun approx-equal(x y)(let ((fuzz-factor 1.0e-6))(or (and (= x 0) (= y 0))(< (/ (abs (- x y))(max (abs x) (abs y)))fuzz-factor))))(approx-equal 1.0e-7 1.0e-12) ;; => t
这段代码采用的是比较相对差距的办法。因为涉及到除法,所以先把二者等于0的情况排除了,避免发生除0的问题。上述代码改造成对应的C代码就是
#define FUZZ_FACTOR 1.0e-6 // 定义误差范围bool approx_equal(double x, double y) {// 处理特殊情况:如果两个数都是 0if (x == 0 && y == 0) {return true;}// 计算相对差并进行比较double relative_difference = fabs(x - y) / fmax(fabs(x), fabs(y));return relative_difference < FUZZ_FACTOR;
}
另外 elisp 中有 eql 函数来判断两个数是否相等
(eql 1 1.0) ;; => nil
(eql 1.0e-7 1.0e-12) ;; => nil
eql 在判断数字时不光判断值,也判断类型。第一条语句,因为二者类型不同,第二条语句二者都是float属于同类型,但是二者的值不同,因此两个结果都是假。
数字的转换
elisp 中可以进行 整形和float型数字的相互转换。在C/C++ 中,整形可以通过隐式转换自动转换成float,而float转换成int时会丢失小数位,比如哪怕是 1.9 在转换为整数时也会是 1。
在elisp中,可以通过float将整数转化为浮点数。例如
(floatp 1) ; ⇒ nil
(floatp (float 1)) ; ⇒ t
(eql (float 1) 1.0) ; ⇒ t
而浮点数转化成整数有下面几个函数
- truncate: 抹除小数位,也就是C/C++语言中float转int的操作
- floor: 类似于C/C++ 中的
floor函数,返回小于等于该数的最大整数 - ceiling: 类似于 C/C++ 中的
ceil函数,返回大于等于该数的最小整数 - round: 类似于 C/C++ 中的
round函数,返回四舍五入后的整数
数的运算
一般的语言,数的运算无外乎 +、-、*、/ 取整、取模。elisp 中同样有这些操作,前面的加减乘除跟其他语言一致,没什么特别的。
C/C++ 以及 elisp 中的除法都不是纯粹数学意义上的除法,它会将结果抹掉小数位转换成整数。我们如果将除数或者被除数转换为float类型的话,那么就得到数学意义上的除法结果 (当然也不全是,毕竟float数据有表达数据的限制)但是python 不一样,它就是纯粹数学意义上的除法。这个设计我也不知道算是好还是不好,毕竟它与其他语言不一致增加了记忆的负担。
(/ 3 2) ; ⇒ 1
(/ (float 3) 2) ; ⇒ 1.5
(/ 3.0 2) ; ⇒ 1.5
C/C++ 中有 ++ 、 -- 操作,而且还分 前++ 和 后++ 。在 elisp 中没有这两个操作,也没有类似于 += 的操作。elisp的赋值一直是用的 setq。而且它提供了 1+ 1- 这两个符号来表示 ++ 和 --。至于是前 ++ 还是 后++ 呢?两个都不是,C/C++中的 ++ 本身具有改变变量值的作用,它们的区别在于是返回值之前改变还是之后改变。而elisp 主要使用 setq 来改变变量的值, 1+ 这个操作无法改变变量的,它仅仅改变这条语句返回的值。例如可以使用下面的代码来测试
(defun inc (num)(1+ num))(setq foo (inc 3)) ;; ⇒ 4
这里将传入的参数加了1,但是其实函数中 num 的值并没有变化,我们可以对函数做一下修改来验证这一点
(defun inc (num)(progn(1+ num)num))(setq foo (inc 3)) ; ⇒ 3
要改变变量的值需要使用 setq 来进行赋值,这个函数可以做一下修改
(defun inc (num)(progn(setq num (1+ num))num))(setq foo (inc 3)) ; ⇒ 4
取模的操作,elisp 中提供了两个方式 % 和 mod 函数,其中 % 与其他语言类似,它要求除数与被除数都是整数,而 mod 则没有这个要求。
我们查看mod函数,发现它是被写在C代码里面的。它虽然也是取余,但是它与数学意义上取余的结果并不一致,例如
(mod -10 3) ;; ⇒ 2
(mod 10 -3) ;; => -2
(% -10 3) ;; ⇒ -1
(% 10 -3) ;; ⇒ 1
% 单纯的就是数学意义上的取模的操作,首先找到商,然后根据商来决定模
而 mod 则不同,mod 中首先一个原则就是余数和除数的符号相同。所以第一个的结果应该是正数 也就是 -3 * 4 + 2 = 10,余数是2。第二个结果应该是 - 3 * (-4) - 2 = 10
mod 还有一个原则,那就是商的结果应该是整数。利用这两个原则我们就可以大概的还原一下计算的过程
(mod 3.5 2) ;; ⇒ 1.5
(mod -3.5 2) ;; ⇒ 0.5
(mod 3.5 -2) ;; ⇒ -0.5
根据上面两个原则,那么它们分别可以还原为
1 * 2 + 1.5 = 3.5-2 * 2 + 0.5 = -3.5-2 * (-2) + 0.5 = 3.5
另外还有一些其他数学上的操作,对于学习后面写配置的话,大多数应该是用不到的。后续需要使用的话再查询就好了,这里就不在多啰嗦了。
到此为止我们已经介绍完了elisp中数的常见操作。后续将陆续介绍其他数据类型,敬请期待。
相关文章:
——elisp 数字类型)
Emacs 折腾日记(五)——elisp 数字类型
本文是参考 emacs lisp 简明教程 写的,很多东西都是照搬里面的内容,如果各位读者觉得本文没有这篇教程优秀或者有抄袭嫌疑、又或者觉得我更新比较慢、再或者其他什么原因,请直接阅读上述链接中的教程。 上一篇我们讲了elisp中的流程控制结构相…...

重拾设计模式--外观模式
文章目录 外观模式(Facade Pattern)概述定义 外观模式UML图作用 外观模式的结构C 代码示例1C代码示例2总结 外观模式(Facade Pattern)概述 定义 外观模式是一种结构型设计模式,它为子系统中的一组接口提供了一个统一…...

源码编译llama.cpp for android
源码编译llama.cpp for android 我这有已经编译好的版本,直接下载使用: https://github.com/turingevo/llama.cpp-build/releases/tag/b4331 准备 android-ndk 已下载: /media/wmx/ws1/software/qtAndroid/Sdk/ndk/23.1.7779620版本 &am…...

StarRocks 排查单副本表
文章目录 StarRocks 排查单副本表方式1 查询元数据,检查分区级的副本数方式2 SHOW PARTITIONS命令查看 ReplicationNum修改副本数命令 StarRocks 排查单副本表 方式1 查询元数据,检查分区级的副本数 # 方式一 查询元数据,检查分区级的副本数…...

Windows11 家庭版安装配置 Docker
1. 安装WSL WSL 是什么: WSL 是一个在 Windows 上运行 Linux 环境的轻量级工具,它可以让用户在 Windows 系统中运行 Linux 工具和应用程序。Docker 为什么需要 WSL: Docker 依赖 Linux 内核功能,WSL 2 提供了一个高性能、轻量级的…...

线程知识总结(二)
本篇文章以线程同步的相关内容为主。线程的同步机制主要用来解决线程安全问题,主要方式有同步代码块、同步方法等。首先来了解何为线程安全问题。 1、线程安全问题 卖票示例,4 个窗口卖 100 张票: class Ticket implements Runnable {priv…...

解决vscode ssh远程连接服务器一直卡在下载 vscode server问题
目录 方法1:使用科学上网 方法2:手动下载 方法3 在使用vscode使用ssh远程连接服务器时,一直卡在下载"vscode 服务器"阶段,但MobaXterm可以正常连接服务器,大概率是网络问题,解决方法如下: 方…...

【Cadence射频仿真学习笔记】IC设计中电感的分析、建模与绘制(EMX电磁仿真,RFIC-GPT生成无源器件及与cadence的交互)
一、理论讲解 1. 电感设计的两个角度 电感的设计可以从两个角度考虑,一个是外部特性,一个是内部特性。外部特性就是把电感视为一个黑盒子,带有两个端子,如果带有抽头的电感就有三个端子,需要去考虑其电感值、Q值和自…...

Definition of Done
Definition of Done English Version The team agrees on, a checklist of criteria which must be met before a product increment “often a user story” is considered “done”. Failure to meet these criteria at the end of a sprint normally implies that the work …...

【漏洞复现】CVE-2023-37461 Arbitrary File Writing
漏洞信息 NVD - cve-2023-37461 Metersphere is an opensource testing framework. Files uploaded to Metersphere may define a belongType value with a relative path like ../../../../ which may cause metersphere to attempt to overwrite an existing file in the d…...

简单工厂模式和策略模式的异同
文章目录 简单工厂模式和策略模式的异同相同点:不同点:目的:结构: C 代码示例简单工厂模式示例(以创建图形对象为例)策略模式示例(以计算价格折扣策略为例)UML区别 简单工厂模式和策…...

HuggingFace datasets - 下载数据
文章目录 下载数据修改默认保存地址 TRANSFORMERS_CACHE保存到本地 & 本地加载保存加载 读取 .arrow 数据 下载数据 1、Python 代码下载 from datasets import load_dataset imdb load_dataset("imdb") # name参数为full或mini,full表示下载全部数…...
和 雅各比矩阵(Jacobian Matrix)的区别和联系:中英双语)
梯度(Gradient)和 雅各比矩阵(Jacobian Matrix)的区别和联系:中英双语
雅各比矩阵与梯度:区别与联系 在数学与机器学习中,梯度(Gradient) 和 雅各比矩阵(Jacobian Matrix) 是两个核心概念。虽然它们都描述了函数的变化率,但应用场景和具体形式有所不同。本文将通过…...

Vscode搭建C语言多文件开发环境
一、文章内容简介 本文介绍了 “Vscode搭建C语言多文件开发环境”需要用到的软件,以及vscode必备插件,最后多文件编译时tasks.json文件和launch.json文件的配置。即目录顺序。由于内容较多,建议大家在阅读时使用电脑阅读,按照目录…...

自定义 C++ 编译器的调用与管理
在 C 项目中,常常需要自动化地管理编译流程,例如使用 MinGW 或 Visual Studio 编译器进行代码的编译和链接。为了方便管理不同编译器和简化编译流程,我们开发了一个 CompilerManager 类,用于抽象编译器的查找、命令生成以及执行。…...
时间管理系统|Java|SSM|JSP|
【技术栈】 1⃣️:架构: B/S、MVC 2⃣️:系统环境:Windowsh/Mac 3⃣️:开发环境:IDEA、JDK1.8、Maven、Mysql5.7 4⃣️:技术栈:Java、Mysql、SSM、Mybatis-Plus、JSP、jquery,html 5⃣️数据库可…...

用SparkSQL和PySpark完成按时间字段顺序将字符串字段中的值组合在一起分组显示
用SparkSQL和PySpark完成以下数据转换。 源数据: userid,page_name,visit_time 1,A,2021-2-1 2,B,2024-1-1 1,C,2020-5-4 2,D,2028-9-1 目的数据: user_id,page_name_path 1,C->A 2,B->D PySpark: from pyspark.sql import SparkSes…...
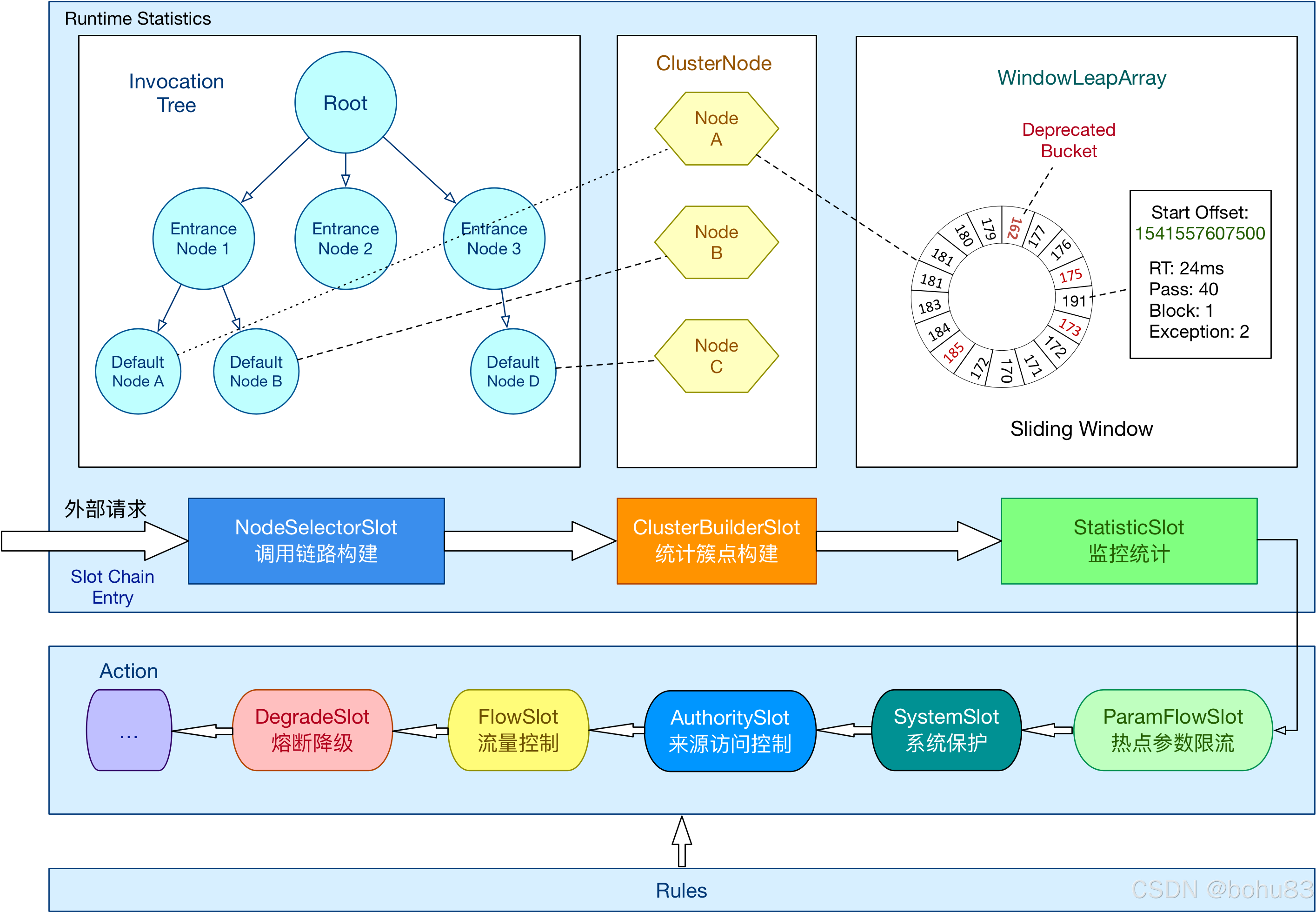
Sentinel 学习笔记3-责任链与工作流程
本文属于sentinel学习笔记系列。网上看到吴就业老师的专栏,原文地址如下: https://blog.csdn.net/baidu_28523317/category_10400605.html 上一篇梳理了概念与核心类:Sentinel 学习笔记2- 概念与核心类介绍-CSDN博客 补一个点:…...

Latex 转换为 Word(使用GrindEQ )(英文转中文,毕业论文)
效果预览 第一步: 告诉chatgpt: 将latex格式中的英文翻译为中文(符号和公式不要动),给出latex格式第二步: Latex 转换为 Word(使用GrindEQ ) 视频 https://www.bilibili.com/video/BV1f242…...

使用Chat-LangChain模块创建一个与用户交流的机器人
当然!要使用Chat-LangChain模块创建一个与用户交流的机器人,你需要安装并配置一些Python库。以下是一个基本的步骤指南和示例代码,帮助你快速上手。 安装依赖库 首先,你需要安装langchain库,它是一个高级框架&#x…...

【HarmonyOS 5.0】DevEco Testing:鸿蒙应用质量保障的终极武器
——全方位测试解决方案与代码实战 一、工具定位与核心能力 DevEco Testing是HarmonyOS官方推出的一体化测试平台,覆盖应用全生命周期测试需求,主要提供五大核心能力: 测试类型检测目标关键指标功能体验基…...

STM32标准库-DMA直接存储器存取
文章目录 一、DMA1.1简介1.2存储器映像1.3DMA框图1.4DMA基本结构1.5DMA请求1.6数据宽度与对齐1.7数据转运DMA1.8ADC扫描模式DMA 二、数据转运DMA2.1接线图2.2代码2.3相关API 一、DMA 1.1简介 DMA(Direct Memory Access)直接存储器存取 DMA可以提供外设…...

什么是库存周转?如何用进销存系统提高库存周转率?
你可能听说过这样一句话: “利润不是赚出来的,是管出来的。” 尤其是在制造业、批发零售、电商这类“货堆成山”的行业,很多企业看着销售不错,账上却没钱、利润也不见了,一翻库存才发现: 一堆卖不动的旧货…...

【android bluetooth 框架分析 04】【bt-framework 层详解 1】【BluetoothProperties介绍】
1. BluetoothProperties介绍 libsysprop/srcs/android/sysprop/BluetoothProperties.sysprop BluetoothProperties.sysprop 是 Android AOSP 中的一种 系统属性定义文件(System Property Definition File),用于声明和管理 Bluetooth 模块相…...
)
C++课设:简易日历程序(支持传统节假日 + 二十四节气 + 个人纪念日管理)
名人说:路漫漫其修远兮,吾将上下而求索。—— 屈原《离骚》 创作者:Code_流苏(CSDN)(一个喜欢古诗词和编程的Coder😊) 专栏介绍:《编程项目实战》 目录 一、为什么要开发一个日历程序?1. 深入理解时间算法2. 练习面向对象设计3. 学习数据结构应用二、核心算法深度解析…...

实战三:开发网页端界面完成黑白视频转为彩色视频
一、需求描述 设计一个简单的视频上色应用,用户可以通过网页界面上传黑白视频,系统会自动将其转换为彩色视频。整个过程对用户来说非常简单直观,不需要了解技术细节。 效果图 二、实现思路 总体思路: 用户通过Gradio界面上…...

【深度学习新浪潮】什么是credit assignment problem?
Credit Assignment Problem(信用分配问题) 是机器学习,尤其是强化学习(RL)中的核心挑战之一,指的是如何将最终的奖励或惩罚准确地分配给导致该结果的各个中间动作或决策。在序列决策任务中,智能体执行一系列动作后获得一个最终奖励,但每个动作对最终结果的贡献程度往往…...

2025年- H71-Lc179--39.组合总和(回溯,组合)--Java版
1.题目描述 2.思路 当前的元素可以重复使用。 (1)确定回溯算法函数的参数和返回值(一般是void类型) (2)因为是用递归实现的,所以我们要确定终止条件 (3)单层搜索逻辑 二…...

起重机起升机构的安全装置有哪些?
起重机起升机构的安全装置是保障吊装作业安全的关键部件,主要用于防止超载、失控、断绳等危险情况。以下是常见的安全装置及其功能和原理: 一、超载保护装置(核心安全装置) 1. 起重量限制器 功能:实时监测起升载荷&a…...

Git 命令全流程总结
以下是从初始化到版本控制、查看记录、撤回操作的 Git 命令全流程总结,按操作场景分类整理: 一、初始化与基础操作 操作命令初始化仓库git init添加所有文件到暂存区git add .提交到本地仓库git commit -m "提交描述"首次提交需配置身份git c…...
