量子退火与机器学习(1):少量数据求解未知QUBO矩阵,以少见多
文章目录
- 前言
- ー、复习QUBO:中药配伍的复杂性
- 1.QUBO 的介入:寻找最佳药材组合
- 二、难题:QUBO矩阵未知的问题
- 1.为什么这么难?
- 三、稀疏建模(Sparse Modeling)
- 1. 欠定系统中的稀疏解
- 2. L1和L2的选择:
- 三、压缩感知算法(Compressed Sensing)
- 1. 压缩感知的性质
- 2. ISTA算法
- 四、Python实现
- 1. 代码和结果解释
- 四、总结
前言
主要是来自大関真之教授的直播课程: 【実践的量子ソリューション創出論・量子力学B・合同補講】第4回: 量子アニーリングによるブラックボックス最適化を実装する【東北大学全学教育・東北大学工学部】
这篇主要讲,怎么用少量数据去推定QUBO矩阵,然后迭代求解未知函数的方法。牵涉的知识如下:
- QUBO建模
- 压缩感知算法(Compressed Sensing)
- 稀疏建模(Sparse Modeling)
- ISTA算法(iterative shrinkage thresholding algorithm:软阈值迭代算法)
ー、复习QUBO:中药配伍的复杂性
提示:仅用公式进行问题描述,太难懂了,就举个例子,不用深究。
中药讲究配伍,即不同药材组合在一起能产生比单一药材更好的疗效,并且能减少副作用。但是,中药材之间的相互作用非常复杂,哪些药材组合在一起能更好地降血压、哪些药材组合会产生不良反应,这些都很难通过传统方式(例如人工经验)进行高效筛选。
1.QUBO 的介入:寻找最佳药材组合
QUBO 是一种数学优化技术,它特别适用于解决组合优化问题。我们可以将中药配伍问题转化为 QUBO 问题,然后利用量子退火或经典计算方法来寻找最佳的药材组合。
QUBO 如何应用于降血压中药配伍:
-
定义二进制变量:
- 对于每一种可能用于降血压的中药材(比如,黄芪、决明子、菊花、钩藤、杜仲等),我们都定义一个二进制变量 x i 。 对于每一种可能用于降血压的中药材(比如,黄芪、决明子、菊花、钩藤、杜仲等),我们都定义一个二进制变量 x_i。 对于每一种可能用于降血压的中药材(比如,黄芪、决明子、菊花、钩藤、杜仲等),我们都定义一个二进制变量xi。
- 如果 x i = 1 ,则表示在最终的配伍中包含这种药材;如果 x i = 0 ,则表示不包含这种药材。 如果 x_i = 1,则表示在最终的配伍中包含这种药材;如果 x_i = 0,则表示不包含这种药材。 如果xi=1,则表示在最终的配伍中包含这种药材;如果xi=0,则表示不包含这种药材。
-
构建目标函数(成本函数):
- 目标函数需要反映出我们希望达成的疗效的综合打分,例如:
- 疗效最大化: 包含能有效降低血压的药材组合。我们可以根据现有研究或实验数据,赋予每个药材一个 “降压能力” 的权重,然后尽可能选择权重高的药材组合。
- 副作用最小化: 避免产生不良反应的药材组合。可以根据文献或实验数据,赋予每个药材一个 “副作用” 的权重,然后尽可能避免选择副作用权重高的药材组合。
- 协同作用最大化: 鼓励选择有协同增效作用的药材组合。可以使用药材之间相互作用的实验数据来计算协同作用,并将其纳入目标函数。
- 因此,目标函数会是这样的形式:
E = ∑ i ( Q i i ∗ x i x i ) ⏟ 对角元素 + ∑ i , j ( i < j ) ( Q i j ∗ x i x j ) ⏟ 上角元素 E = \underbrace{\sum_i(Q_{ii} * x_ix_i)}_{对角元素} + \underbrace{\sum_{i,j(i<j)}(Q_{ij} * x_ix_j)}_{上角元素} E=对角元素 i∑(Qii∗xixi)+上角元素 i,j(i<j)∑(Qij∗xixj)- x i 是二进制变量,表示是否使用第 i 种药材。 x_i是二进制变量,表示是否使用第i种药材。 xi是二进制变量,表示是否使用第i种药材。
- Q i i 代表第 i 种药材的个体权重 ( 例如,降压能力、副作用 ) 。 Q_{ii}代表第i种药材的个体权重 (例如,降压能力、副作用)。 Qii代表第i种药材的个体权重(例如,降压能力、副作用)。
- Q i j 代表第 i 种和第 j 种药材的相互作用权重 ( 例如,协同作用或不良反应 ) 。 Q_{ij}代表第i种和第j种药材的相互作用权重 (例如,协同作用或不良反应)。 Qij代表第i种和第j种药材的相互作用权重(例如,协同作用或不良反应)。
- 目标是找到能使 Q 的值最小化的 xi 的组合。
- 目标函数需要反映出我们希望达成的疗效的综合打分,例如:
-
约束条件:
- 有些情况下,我们可能需要加入一些约束条件,例如:
- 配方中药材的总数不超过某个值(例如不超过5种)。
- 必须包含某几种基础药材。
- 必须避免某些药材同时出现。
- 这些约束条件也会被转化为 QUBO 中的惩罚项(添加到目标函数中),以确保优化结果满足要求。
- 有些情况下,我们可能需要加入一些约束条件,例如:
-
优化:
- 使用量子退火器,寻找使 QUBO 目标函数 E 最小化的二进制变量
x组合。 - 计算出的 x_i 的值(0或1)就对应着最佳的配伍组合。
- 使用量子退火器,寻找使 QUBO 目标函数 E 最小化的二进制变量
二、难题:QUBO矩阵未知的问题
1.为什么这么难?
-
很多问题没有确定的QUBO矩阵
比如,中药配伍的问题,你不能通过像TSP问题那样,已经知道地点位置,地点间距离,相应的约束条件。 -
获得验证数据的周期太长或者难度太大。
比如,中药配伍的话,你收集一个配方的实验数据,就需要很多人力物力,这样成本代价太高了,不能无限的验证下去。
已经有少量数据的情况下,怎么近似求解QUBO?
- 思路如下图:

数据足够多的话,是不是可以解方程。比如,中药配伍问题的情况,各变量的含义如下:
x变量就是用或者不用某位药,n维就代表有n种药。b变量就是每次不同中药组合的测量后的综合药效列表,假定有m个。a就是每次不同的QUBO矩阵上三角里的元素n列表。a是无数种可能的,但是里面肯定有一个是我们想要的接近现实的解。

上面的式子有的难懂,给大家举个实例。x
| x_type | value |
|---|---|
| x₁ | 1 |
| x₂ | 0 |
| x₃ | 1 |
| x₁x₂ | 0 |
| x₁x₃ | 1 |
| x₂x₃ | 0 |
a
| a⁽¹⁾ | a⁽²⁾ | a⁽³⁾ | a⁽⁴⁾ | a⁽⁵⁾ | a⁽⁶⁾ | |
|---|---|---|---|---|---|---|
| a₁ | 0.5 | -0.3 | 0.8 | -0.4 | 0.6 | -0.7 |
| a₂ | -0.6 | 0.7 | -0.2 | 0.5 | -0.8 | 0.2 |
| a₃ | 0.4 | -0.5 | 0.9 | -0.6 | 0.3 | -0.4 |
b
| b | value |
|---|---|
| b₁ | 1.9 |
| b₂ | -1.6 |
| b₃ | 1.6 |
上面的式子变换一下:

下面解释一下变换后的式子中各个变量的维度:
-
向量 b 是 m 维向量: b ∈ ℝᵐ
-
矩阵 A = [a⁽¹⁾, …, a⁽ⁿ⁾] 的维度是:
- 每个 a⁽ⁱ⁾ 是 m 维向量
- 一共有 n 个这样的向量
- 所以 A 的维度是 m × n
-
x是 n(n+1)/2 维向量(QUBO矩阵的上三角里所有元素): x ∈ R n ( n + 1 ) / 2 x ∈ ℝ^{n(n+1)/2} x∈Rn(n+1)/2
-
通过矩阵乘法 Ax:
- A(m×n) × x(n×1) = b(m×1)
- 结果 b 是 m 维向量,与原始定义一致
三、稀疏建模(Sparse Modeling)
线性方程组大家都知道,学完线性代数,也都知道可以换成矩阵形式。我就直接贴上wiki截图了。
https://zh.wikipedia.org/zh-cn/%E7%BA%BF%E6%80%A7%E6%96%B9%E7%A8%8B%E7%BB%84

- 一般情况下,1个方程解1个未知数,2个方程解2个未知数,这是我们平时接触较多的求解线性系统的情况,称之为适定系统。
那如果,一个方程有两个未知数呢?这种情况就是欠定系统了。
在压缩感知理论中,一般用下列式子来表示一个欠定系统:
b = A x \mathbf{b} = \mathbf{A} \mathbf{x} b=Ax
其中 R M × N , X ∈ R M , b ∈ R N . 且当 M < N 时,系统维欠定系统 . 其中\mathbb{R}^{M \times N}, X \in \mathbb{R}^M, b \in \mathbb{R}^N. 且当M < N时,系统维欠定系统. 其中RM×N,X∈RM,b∈RN.且当M<N时,系统维欠定系统.
方程组的数量不足意味着决定解的条件不足。由于条件不足,如果再增加一些条件就可以确定解。
例如,如果预先知道解,通过将其代入,就可以有效地减少N。现在假设已知解,且x的各分量几乎为0。
在这种情况下,可以从方程组中删除值为0的分量。如果将非零项的数量记为K,那么从M个方程实际上就是求解K个非零分量,即使M < N,只要M > K,就可以求解。
这种大部分分量为零或预期为零的性质称为"稀疏性",具有这种性质的解称为"稀疏解"。
1. 欠定系统中的稀疏解
下面的所有截图都在这个日文资料里:https://www-adsys.sys.i.kyoto-u.ac.jp/mohzeki/Presentation/lecturenote20160727.pdf
对于N维的未知向量x,M维的实数值向量b和M × N的观测矩阵A,假设满足以下关系:
这里即使M < N,当x的分量中大部分为零(具有稀疏性)时,如果非零分量的数量K满足M > K,就可以求得解。
然而,这K个非零分量究竟在哪里?这是未知的。那么如何求解呢?
虽然遗憾,但没有决定性的方法,只能从N个分量中选取K个分量,寻找满足y = Ax的解。从N个中选取K个的组合数,随着N的增大会呈指数级增长。对于高维问题,进行这样的计算在现实中是不可行的。而且虽然说是K个非零项,但K这个数字真的已知吗?这也不一定知道。
因此,当这些非零分量的数量也未知时,应该采取什么样的策略来寻找满足b = Ax的解呢?
其实就是用各种正则化L0,L1,L2正则。
-
L0正则:

∥ x ∥ 0 ,代表非 0 解的个数。越小越稀疏。 \|\mathbf{x}\|_0,代表非0解的个数。越小越稀疏。 ∥x∥0,代表非0解的个数。越小越稀疏。 -
L1正则:

∥ x ∥ 1 = ∣ x 1 ∣ + ∣ x 2 ∣ + ⋯ + ∣ x N ∣ , 代表 x 的绝对值总和。 0 越多, ∥ x ∥ 1 越小越稀疏。 \|\mathbf{x}\|_1 = |x_1| + |x_2| + \cdots + |x_N|, 代表x的绝对值总和。0越多,\|\mathbf{x}\|_1越小越稀疏。 ∥x∥1=∣x1∣+∣x2∣+⋯+∣xN∣,代表x的绝对值总和。0越多,∥x∥1越小越稀疏。 -
L2正则:

∥ x ∥ 2 = x 1 2 + x 2 2 + ⋯ + x N 2 \|\mathbf{x}\|_2 = \sqrt{x_1^2 + x_2^2 + \cdots + x_N^2} ∥x∥2=x12+x22+⋯+xN2
2. L1和L2的选择:

下面的图是一个L1和L2求解的结果,明显L1成功获得了真实解,L2失败。

三、压缩感知算法(Compressed Sensing)
根据正则的性质,我们已经知道可以获得这样的解选择技术。
- 这时需要思考的问题是:我们真的需要稀疏解吗?真正的解是稀疏解吗?
- 前者关注的是变量选择的问题。当我们对方程的真实解不感兴趣,而只是在寻找能满足方程的最少变量组合时,这是一个重要的问题。
- 至于后者,当我们不是要选择变量而是要寻找真实解时,就需要考虑稀疏解是否合适。对于本质上具有稀疏解的方程问题,有选择性地找出稀疏解会产生巨大的效果。
压缩感知这个框架是利用正则的特性从欠定方程组中获得稀疏解,从而更准确地确定我们想要了解的内容。它就像信息科学中的名侦探。
特别是,通过L1范数最小化来估计原始信息的方法被称为基追踪(Basis Pursuit)。
1. 压缩感知的性质
当观测矩阵A的各分量从均值为0、方差为1的高斯分布生成时,以下列曲线为边界,在α较大且ρ较小的区域内,通过L1正则最小化可以以极高的概率成功恢复原始信号。其中α = M/N,ρ = K/NP,Q(t)是标准正态分布的尾部概率积分。
1 α = 1 + π 2 t e t 2 2 { 1 − 2 Q ( t ) } \frac{1}{\alpha} = 1 + \sqrt{\frac{\pi}{2}}te^{\frac{t^2}{2}}\{1-2Q(t)\} α1=1+2πte2t2{1−2Q(t)}
ρ 1 − ρ = 2 ( e − t 2 2 t 2 π − Q ( t ) ) \frac{\rho}{1-\rho} = 2\left(\frac{e^{-\frac{t^2}{2}}}{t\sqrt{2\pi}}-Q(t)\right) 1−ρρ=2(t2πe−2t2−Q(t))
Q ( t ) = ∫ t ∞ e − x 2 2 2 π d x Q(t) = \int_t^{\infty}\frac{e^{-\frac{x^2}{2}}}{\sqrt{2\pi}}dx Q(t)=∫t∞2πe−2x2dx
α = M N , ρ = K N \alpha = \frac{M}{N}, \quad \rho = \frac{K}{N} α=NM,ρ=NK

上图展示了压缩感知中L1正则最小化重构的可行性边界。让我详细解释一下:
- 坐标轴含义:
- 横轴 ρ = K/N:表示稀疏度(信号中非零元素的比例)
- 纵轴 α = M/N:表示测量数与信号维度的比值(压缩比)
- 图中的区域:
- 蓝色区域:这是L1范数最小化能够成功重构原始信号的区域
- 当(ρ,α)点落在这个区域内时,我们可以以很高的概率通过L1最小化重构出原始信号
- 特别是在α较大(即测量数较多)且ρ较小(即信号较稀疏)的情况下,重构成功率最高
- 分界线:
- 实线曲线:表示L1重构的理论边界
- 虚线 α = ρ:这条对角线表示测量数等于非零元素个数的情况
- 实际意义:
- 这个图帮助我们理解在给定信号稀疏度ρ的情况下,需要多少测量值(由α决定)才能成功重构
- 在蓝色区域内,压缩感知是有效的,即可以用少量测量重构出原始信号
- 区域外则表示测量数不足,无法保证信号重构的成功
这个图对于实际应用压缩感知非常有用,它可以帮助我们确定所需的最小测量数,以保证可以成功重构具有特定稀疏度的信号。下面这句话很重要,我说三遍。
- 压缩感知,重要的不仅仅是选择稀疏解,关键在于不能仅仅是选择"差不多"解,还需要其中包含正确答案。
- 压缩感知,重要的不仅仅是选择稀疏解,关键在于不能仅仅是选择"差不多"解,还需要其中包含正确答案。
- 压缩感知,重要的不仅仅是选择稀疏解,关键在于不能仅仅是选择"差不多"解,还需要其中包含正确答案。
2. ISTA算法
ISTA是一个通过L1正则化,迭代求解欠定系统的算法,流程如下(证明自己网上可查):
-
令t = 0,初始化x[0]。例如可以设置 x [ 0 ] = A T y x[0] = A^T y x[0]=ATy
-
通过平方完成法求解g(x)的二次函数近似的顶点:
v [ t ] = x [ t ] + ( 1 / L λ ) A T ( y − A x [ t ] ) v[t] = x[t] + (1/Lλ)A^T(y - Ax[t]) v[t]=x[t]+(1/Lλ)AT(y−Ax[t]) -
应用软阈值函数:
x [ t + 1 ] = S 1 / L ( v [ t ] ) x[t+1] = S_{1/L}(v[t]) x[t+1]=S1/L(v[t]) -
重复步骤2-4直到满足终止条件。
四、Python实现
import numpy as np
import matplotlib.pyplot as plt
from openjij import SASampler
from IPython.display import clear_outputdef grad_comp(y, A, x):"""计算梯度Args:y: 观测值向量A: 测量矩阵x: 当前解向量Returns:grad: 梯度向量"""grad = -np.dot(A.T, (y - A.dot(x)))return graddef SoftThr(v, thr):"""软阈值函数实现Args:v: 输入向量thr: 阈值Returns:z: 经过软阈值处理的向量"""z = np.zeros(len(v))# 处理大于阈值的元素itemp = np.where(v > thr)z[itemp] = v[itemp] - thr# 处理小于-阈值的元素itemp = np.where(v <= -thr)z[itemp] = v[itemp] + thrreturn zdef opt_qvec(x, x0, y, A, Tall=10, p=10.0, flag=True):"""使用ADMM算法优化QUBO向量Args:x: 初始解向量x0: 目标解向量y: 观测值向量A: 测量矩阵Tall: 最大迭代次数p: ADMM惩罚参数flag: 是否显示优化过程图像Returns:x: 优化后的解向量"""N = A.shape[0]# 计算A的伪逆相关矩阵Atemp = A.dot(A.T)Ainv = np.linalg.inv(Atemp)Atemp = A.T.dot(Ainv)Nvec = len(x)# ADMM算法的辅助变量z = np.zeros(Nvec)u = np.zeros(Nvec)# ADMM迭代for t in range(Tall):# 更新xx = Atemp.dot(y) + (np.eye(Nvec) - Atemp.dot(A)).dot(z + u)# 更新z(软阈值步骤)z = SoftThr(x - u, 1/p)# 更新对偶变量uu = u + (z - x)# 如果需要,绘制优化过程if flag:clear_output(True)plt.plot(x)plt.plot(x0)plt.show()return xdef Xmat_make(x):"""构造QUBO问题的特征向量Args:x: 输入向量Returns:Xvec: 包含一阶项和二阶项的特征向量"""Ns = len(x)# 向量长度为一阶项数量加上二阶项数量Xvec = np.zeros(Ns + Ns*(Ns-1)//2)# 填充一阶项t = 0for i in range(Ns):Xvec[t] = x[i]t = t + 1# 填充二阶项(交互项)for i in range(Ns):for j in range(Ns):if i < j:Xvec[t] = x[i]*x[j]t = t + 1return Xvecdef ycomp(Xvec, Qvec):"""计算QUBO问题的能量Args:Xvec: 特征向量Qvec: QUBO系数向量Returns:Ene: 能量值"""Ene = np.dot(Xvec, Qvec)return Enedef QUBO_create(Qvec, Ns):"""从向量形式构造QUBO矩阵Args:Qvec: QUBO系数向量Ns: 系统大小Returns:QUBO: QUBO矩阵"""# 计算二阶项数量Noff = (Ns*(Ns-1))//2# 提取对角项(一阶项)和非对角项(二阶项)Qdiag = Qvec[:Ns]Qoff = Qvec[Ns:]# 构造QUBO矩阵QUBO = np.diag(Qdiag)# 填充非对角元素t = 0for i in range(Ns):for j in range(Ns):if i < j:QUBO[i,j] = Qoff[t]t = t + 1return QUBO# 主程序开始# 设置系统大小
Ns = 20# 生成随机的QUBO问题
# 生成对角项
Qdiag = np.random.randn(Ns)
QUBO = np.diag(Qdiag)# 生成稀疏的非对角项
Noff = (Ns*(Ns-1))//2
Qoff = np.random.randn(Noff)
rho = 0.2 # 稀疏度参数
mask = (np.random.rand(Noff) < rho)
Qoff = mask*Qoff# 合并对角项和非对角项
Qvec = np.concatenate((Qdiag,Qoff))# 生成训练数据
M = 100 # 训练样本数
Adata = [] # 特征矩阵
ydata = [] # 能量值# 随机生成训练样本
for d in range(M):# 生成随机二值向量x = (np.random.rand(Ns) > 0.5)x = x.astype(np.int16)# 计算特征向量和对应能量Xvec = Xmat_make(x)Ene = ycomp(Xvec,Qvec)Adata.append(Xvec)ydata.append(Ene)# 将数据转换为numpy数组
y = np.array(ydata)
A = np.array(Adata)# 使用ADMM算法学习QUBO参数
Nvec = Noff + Ns
Qinf = np.zeros(Nvec)
Qinf = opt_qvec(Qinf, Qvec, y, A, Tall=100)# 构造学习到的QUBO矩阵
QUBO = QUBO_create(Qinf, Ns)# 使用量子退火采样器求解QUBO问题
sampler = SASampler()
sampleset = sampler.sample_qubo(QUBO, num_reads=1)# 迭代优化过程
Ns = 20
Ndata = 5 # 初始数据点数
Nall = 195 # 总迭代次数# 初始化数据集
Adata = []
ydata = []for d in range(Ndata):x = (np.random.rand(Ns) > 0.5)x = x.astype(np.int16)Xvec = Xmat_make(x)Ene = ycomp(Xvec,Qvec)Adata.append(Xvec)ydata.append(Ene)# 记录优化过程中的能量
Enelist = []
Eneminlist = []
xlist = []
Qinf = np.dot(A.T,y)# 主优化循环
for d in range(Nall):# 更新QUBO参数y = np.array(ydata)A = np.array(Adata)Qinf = opt_qvec(Qinf, Qvec, y, A, Tall=10, flag=False)QUBO = QUBO_create(Qinf, Ns)# 使用量子退火采样器获得新解sampleset = sampler.sample_qubo(QUBO, num_reads=1)x = sampleset.record[0][0]# 检查是否重复解for xtemp in xlist:if np.array_equal(x,xtemp):x = (np.random.rand(Ns) > 0.5)x = x.astype(np.int16)breakxlist.append(x)# 计算新解的能量Xvec = Xmat_make(x)Ene = ycomp(Xvec,Qvec)Enelist.append(Ene)Enemin = np.min(Enelist)Eneminlist.append(Enemin)# 更新数据集ydata.append(Ene)Adata.append(Xvec)# 绘制优化过程clear_output(True)plt.plot(Enelist)plt.plot(Eneminlist)plt.show()
1. 代码和结果解释
1.1 代码细节
代码其实挺简化,但我们也可以从中看到一些细节:
Noff = int((Ns * (Ns - 1)) / 2)计算了QUBO矩阵中非对角线的个数。mask的作用是只考虑稀疏的那些Qij。np.random.rand(Ns)在模拟实验中用于产生随机的01向量。opt_qvec是关键的函数,里面通过数据拟合Q矩阵,并用此Q矩阵进行退火优化。
1.2 总体思路回顾:
- 目标: 使用模拟退火算法(SA)或者量子退火算法(QA)来找到一个QUBO问题的最优解,但QUBO矩阵本身是未知的(“黑盒”)。
- 难点: QUBO矩阵是未知的,我们无法直接使用标准的退火方法。
- 解决方法: 使用压缩感知算法,逐步猜测和逼近真实的QUBO矩阵,并在这个过程中利用退火算法进行优化。
- 关键: 从客户(黑盒)那里获得数据,然后用这些数据来推断Q矩阵。
1.3 压缩感知算法的应用:
使用压缩感知算法的核心体现在opt_qvec函数内部和整个迭代过程中,它的思想是:
- 稀疏性假设: 假设QUBO矩阵是稀疏的(即有很多元素为零)。
- 数据采集: 通过不断询问(比如做问卷,问专家)黑盒获取数据,可以理解为通过不断迭代模拟退火算法来寻找更好的01向量。
- 逐步逼近: 使用采集到的数据,反推(拟合)出一个稀疏的QUBO矩阵。
- 更新和迭代: 然后使用这个推导出的Q矩阵进行退火,并继续这个采样拟合的过程,直到找到一个比较好的Q矩阵来推断。
1.4 最后的输出结果解读:

- 最终图像部分:
- x轴表示退火优化的迭代步骤,y轴表示能量值。
- 蓝色曲线:表示模拟退火算法在尝试优化(寻找更低的能量)过程中,每个采样点所对应的能量值
- 橘色曲线:真实情况的能量值,用来对比模拟退火算法找到的解和真实解之间的差距。
- 解读:
- 数据与优化协同作用: 这种蓝色线和黄色线的同步下降,生动地展示了压缩感知算法的核心——通过模拟退火(或量子退火)算法的优化搜索,不断引导QUBO矩阵的逼近,同时利用新的01向量的数据,使推导的矩阵越来越精确,最终在黑盒优化问题中找到好的解。
- 蓝色尖峰出现: 蓝色线的尖峰,通常表示模拟退火算法在搜索过程中,随机尝试到了一个能量比较高的状态。这是退火算法的探索性的一部分,它会尝试从当前的局部最优解“跳出”,看看是否有更低的能量值。这种尖峰通常表示对目前解的否定。
四、总结
这个教程,真的是很直观地讲解了最先进的QUBO建模技术,以少见多。有什么问题,欢迎指正。
下一篇,更深入的讲解ISTA算法的升级版ADMM算法
相关文章:

量子退火与机器学习(1):少量数据求解未知QUBO矩阵,以少见多
文章目录 前言ー、复习QUBO:中药配伍的复杂性1.QUBO 的介入:寻找最佳药材组合 二、难题:QUBO矩阵未知的问题1.为什么这么难? 三、稀疏建模(Sparse Modeling)1. 欠定系统中的稀疏解2. L1和L2的选择: 三、压缩感知算法(C…...
)
矩阵:Input-Output Interpretation of Matrices (中英双语)
矩阵的输入-输出解释:深入理解与应用 在线性代数中,矩阵与向量的乘积 ( y A x y Ax yAx ) 是一个极为重要的关系。通过这一公式,我们可以将矩阵 ( A A A ) 看作一个将输入向量 ( x x x ) 映射到输出向量 ( y y y ) 的线性变换。在这种…...

excel 使用vlook up找出两列中不同的内容
当使用 VLOOKUP 函数时,您可以将其用于比较两列的内容。假设您要比较 A 列和 B 列的内容,并将结果显示在 C 列,您可以在 C1 单元格中输入以下公式: 这个公式将在 B 列中的每个单元格中查找是否存在于 A 列中。如果在 A 列中找不到…...

YoloV8改进策略:Head改进|DynamicHead,利用注意力机制统一目标检测头部|即插即用
摘要 论文介绍 本文介绍了一种名为DynamicHead的模块,该模块旨在通过注意力机制统一目标检测头部,以提升目标检测的性能。论文详细阐述了DynamicHead的工作原理,并通过实验证明了其在COCO基准测试上的有效性和效率。 创新点 DynamicHead模块的创新之处在于它首次尝试在一…...
两地的日出日落时间差为啥不相等
悟空去延吉玩耍,在下午4点多的时候发来一张照片,说,天已经黑了!我赶紧地图上看了看,延吉居然和北京差了大约15度的经度差,那就是大约一小时的时差哦。次日我随便查了一下两地的日出日落时间,结果…...

Android Https和WebView
系统会提示说不安全,因为网站通过js就能调用你的android代码,如果你确认你的网站没用到JS的话就不要打开这个开关,如果用到了,就添加一个注解忽略它就行了。 后来就使用我们公司的网站了,发现也出不来,后来…...
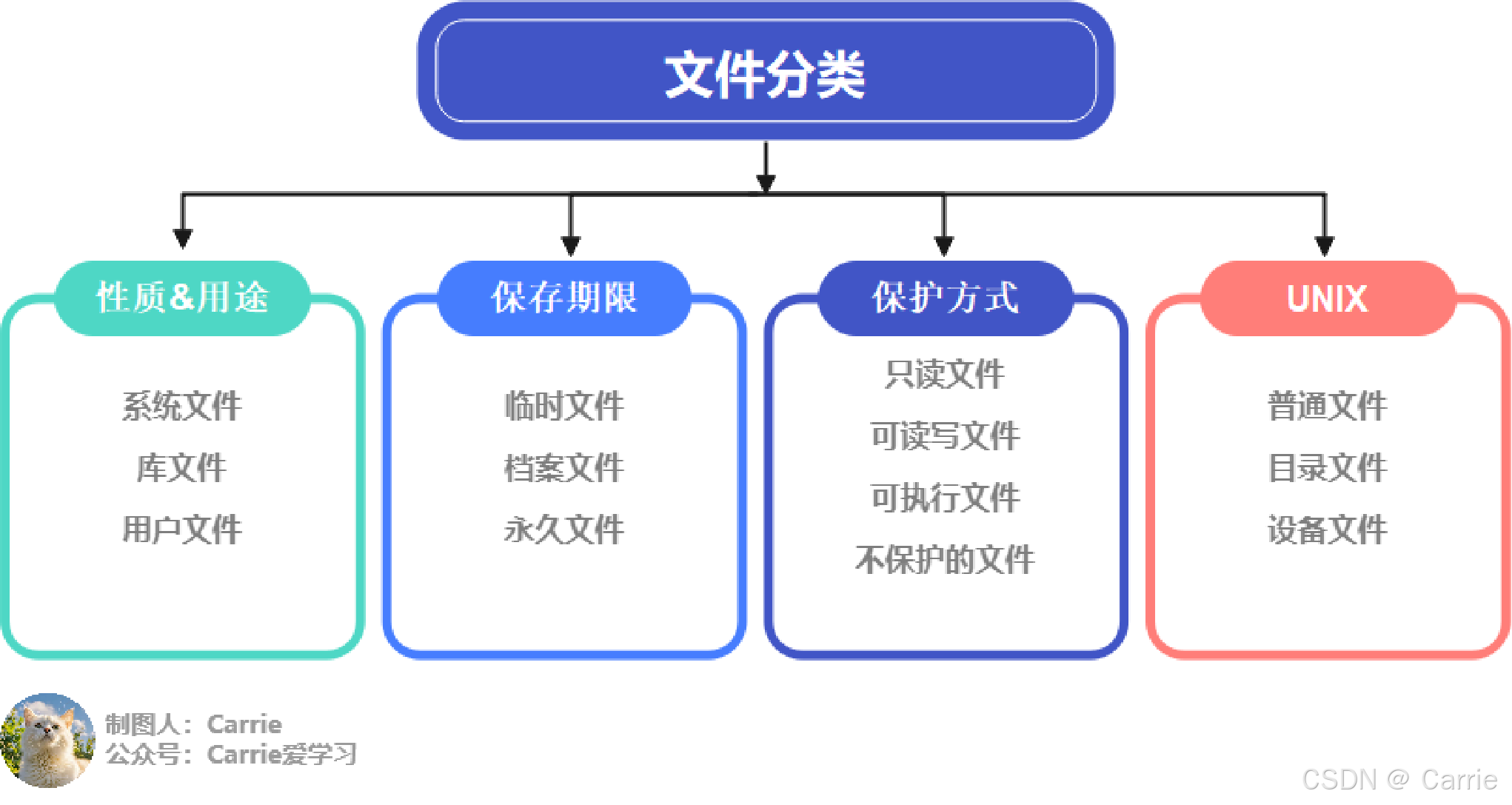
2.5.1 文件管理基本概念
文章目录 文件文件系统文件分类 文件 文件:具有符号名,逻辑上有完整意义的一组相关信息的集合。 文件包含文件体、文件说明两部分。文件体存储文件的真实内容,文件说明存放操作系统管理文件所用的信息。 文件说明包含文件名、内部标识、类型、…...
在 PowerShell 中优雅地显示 Python 虚拟环境
在使用 Python 进行开发时,虚拟环境管理是一个非常重要的部分。无论是使用 venv 还是 conda,我们都希望能够清晰地看到当前所处的虚拟环境。本文将介绍如何在 PowerShell 中配置提示符,使其能够优雅地显示不同类型的 Python 虚拟环境。 问题…...
K8S Ingress 服务配置步骤说明
部署Pod服务 分别使用kubectl run和kubectl apply 部署nginx和tomcat服务 # 快速启动一个nginx服务 kubectl run my-nginx --imagenginx --port80# 使用yaml创建tomcat服务 kubectl apply -f my-tomcat.yamlmy-tomcat.yaml apiVersion: apps/v1 kind: Deployment metadata:n…...
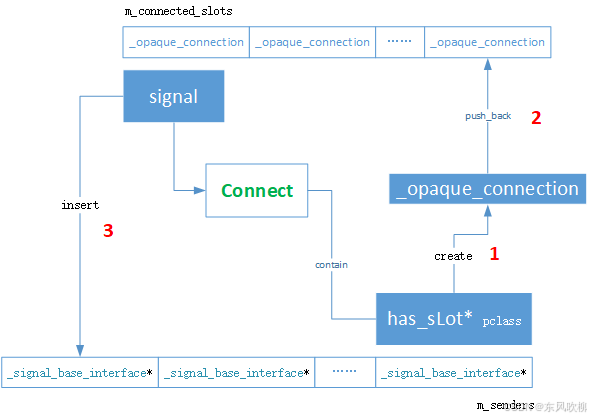
观察者模式(sigslot in C++)
大家,我是东风,今天抽点时间整理一下我很久前关注的一个不错的库,可以支持我们在使用标准C的时候使用信号槽机制进行观察者模式设计,sigslot 官网: http://sigslot.sourceforge.net/ 本文较为详尽探讨了一种观察者模…...

python使用pip进行库的下载
前言 现如今有太多的python编译软件,其库的下载也是五花八门,但在作者看来,无论是哪种方法都是万变不离其宗,即pip下载。 pip是python的包管理工具,无论你是用的什么python软件,都可以用pip进行库的下载。 …...
)
C#(委托)
一、基本定义 在C#中,委托(Delegate)是一种引用类型,它用于封装一个方法(具有特定的参数列表和返回类型)。可以把委托想象成一个能存储方法的变量,这个变量能够像调用普通方法一样来调用它所存…...

《点点之歌》“意外”诞生记
世界是“点点”的,“点点”是世界的。 (笔记模板由python脚本于2024年12月23日 19:28:25创建,本篇笔记适合喜欢诗文的coder翻阅) 【学习的细节是欢悦的历程】 Python 官网:https://www.python.org/ Free:大咖免费“圣经”教程《 …...
ue5 pcg(程序内容生成)真的简单方便,就5个节点
总结: 前情提示 鼠标单击右键平移节点 1.编辑-》插件-》procedural->勾选两个插件 2.右键-》pcg图表-》拖拽进入场景 3.先看点point 右键-》调试(快捷键d)->右侧设置粒子数 3.1调整粒子数 可以在右侧输入框,使用加减乘除 4.1 表面采样器 …...

32岁前端干了8年,是继续做前端开发,还是转其它工作
前端发展有瓶颈,变来变去都是那一套,只是换了框架换了环境。换了框架后又得去学习,虽然很快上手,但是那些刚毕业的也很快上手了,入门门槛越来越低,想转行或继续卷,该如何破圈 这是一位网友的自述…...
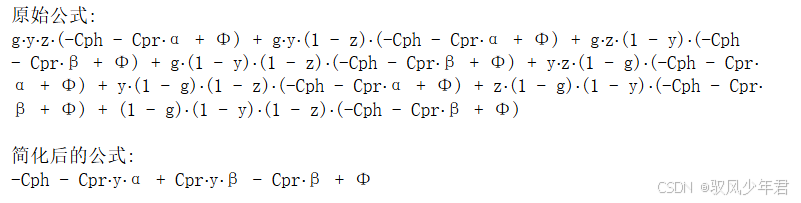
【演化博弈】期望收益函数公式、复制动态方程——化简功能技巧
期望化简 在演化博弈论的研究中,期望收益函数和复制动态方程是核心工具。化简这些公式的功能技巧具有以下几个重要作用: 提高公式的可读性和理解度 复杂的数学表达式可能让人感到困惑。通过化简,公式变得更加简单和易读,使研究者…...

opencv中的各种滤波器简介
在 OpenCV 中,滤波器是图像处理中的重要工具,用于对图像进行平滑、去噪、边缘检测等操作。以下是几种常见滤波器的简单介绍。 1. 均值滤波 (Mean Filter) 功能: 对图像进行平滑处理,减少噪声。 应用场景: 去除图像…...

[Effective C++]条款36-37 两个绝不
本文初发于 “天目中云的小站”,同步转载于此。 条款36 : 绝不重新定义继承而来的non-virtual函数 本条款很容易理解, 援引以前的条款就可以说明为什么 : 条款34中就提到过 : non-virtual函数意味着接口 强制性实现继承, 它不应当被改变. 重新定义继承而来的non-…...
)
各种网站(学习资源及其他)
欢迎围观笔者的个人博客~ 也欢迎通过RSS网址https://kangaroogao.github.io/atom.xml进行订阅~ 大学指南 上海交通大学生存手册中国科学技术大学人工智能与数据科学学院本科进阶指南USTC不完全入学指南大学生活质量指北科研论 信息搜集 AI信息搜集USTC飞跃网站计算机保研 技…...

docker怎么部署高斯数据库
部署高斯数据库(openGauss)到Docker的步骤如下: 安装Docker: 如果您的系统尚未安装Docker,需要先进行安装。以CentOS为例,可以使用以下命令安装Docker: yum install -y docker拉取镜像ÿ…...

遍历 Map 类型集合的方法汇总
1 方法一 先用方法 keySet() 获取集合中的所有键。再通过 gey(key) 方法用对应键获取值 import java.util.HashMap; import java.util.Set;public class Test {public static void main(String[] args) {HashMap hashMap new HashMap();hashMap.put("语文",99);has…...

汽车生产虚拟实训中的技能提升与生产优化
在制造业蓬勃发展的大背景下,虚拟教学实训宛如一颗璀璨的新星,正发挥着不可或缺且日益凸显的关键作用,源源不断地为企业的稳健前行与创新发展注入磅礴强大的动力。就以汽车制造企业这一极具代表性的行业主体为例,汽车生产线上各类…...

376. Wiggle Subsequence
376. Wiggle Subsequence 代码 class Solution { public:int wiggleMaxLength(vector<int>& nums) {int n nums.size();int res 1;int prediff 0;int curdiff 0;for(int i 0;i < n-1;i){curdiff nums[i1] - nums[i];if( (prediff > 0 && curdif…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院查看报告小程序
一、开发环境准备 工具安装: 下载安装DevEco Studio 4.0(支持HarmonyOS 5)配置HarmonyOS SDK 5.0确保Node.js版本≥14 项目初始化: ohpm init harmony/hospital-report-app 二、核心功能模块实现 1. 报告列表…...

JDK 17 新特性
#JDK 17 新特性 /**************** 文本块 *****************/ python/scala中早就支持,不稀奇 String json “”" { “name”: “Java”, “version”: 17 } “”"; /**************** Switch 语句 -> 表达式 *****************/ 挺好的ÿ…...

RNN避坑指南:从数学推导到LSTM/GRU工业级部署实战流程
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文全面剖析RNN核心原理,深入讲解梯度消失/爆炸问题,并通过LSTM/GRU结构实现解决方案,提供时间序列预测和文本生成…...

莫兰迪高级灰总结计划简约商务通用PPT模版
莫兰迪高级灰总结计划简约商务通用PPT模版,莫兰迪调色板清新简约工作汇报PPT模版,莫兰迪时尚风极简设计PPT模版,大学生毕业论文答辩PPT模版,莫兰迪配色总结计划简约商务通用PPT模版,莫兰迪商务汇报PPT模版,…...

【Linux手册】探秘系统世界:从用户交互到硬件底层的全链路工作之旅
目录 前言 操作系统与驱动程序 是什么,为什么 怎么做 system call 用户操作接口 总结 前言 日常生活中,我们在使用电子设备时,我们所输入执行的每一条指令最终大多都会作用到硬件上,比如下载一款软件最终会下载到硬盘上&am…...

《Docker》架构
文章目录 架构模式单机架构应用数据分离架构应用服务器集群架构读写分离/主从分离架构冷热分离架构垂直分库架构微服务架构容器编排架构什么是容器,docker,镜像,k8s 架构模式 单机架构 单机架构其实就是应用服务器和单机服务器都部署在同一…...

Vue3中的computer和watch
computed的写法 在页面中 <div>{{ calcNumber }}</div>script中 写法1 常用 import { computed, ref } from vue; let price ref(100);const priceAdd () > { //函数方法 price 1price.value ; }//计算属性 let calcNumber computed(() > {return ${p…...
