关于内网服务器依托可上网电脑实现访问互联网
关于内网服务器依托可上网电脑实现访问互联网
背景:在实验室内网的一个服务器,没有配置 NAT ,无法使用外网,只能在局域网内进行访问,但是呢,我们自己的电脑是可以访问互联网的,那么怎么通过让自己的电脑作为服务器的代理,让服务器访问互联网呢?这往往是非常重要的,服务器上往往要跑实验,但是实验跑起来需要下载,所以代理就必不可少了
原理简单讲一下我的理解吧:
- 首先服务器本身不能连接互联网,但是我们自己的电脑在同一个局域网内,但是自己的电脑连接的路由器配置了NAT故可以访问外网,现在需要的就是服务器可以访问互联网,怎么做到呢?
- 把自己的电脑作为一个中转站即可,因为服务器和自己的电脑在同一个局域网中,所以可以互相通信,当服务器要访问互联网时,在服务器中配置,把所有访问互联网的请求都转发给自己的电脑,然后自己的电脑再转发出去,得到结果以后,自己的电脑再转发给服务器,这样就完成了访问互联网了。
没开代理的情况:
第一步下载一个代理软件
比如 Clash,CCProxy
然后开启代理功能

第二步设置代理
# 设置 http、https 代理
export http_proxy=http://<Your IP>:<Your Port> # 这里的端口如果你选择Clash的话一般就是 7890,还需要在自己电脑上设置防火墙,把7890端口进行开放
export https_proxy=http://<Your IP>:<Your Port># 设置 conda 代理
conda config --set proxy_http <proxy_address>:<proxy_port>
conda config --set proxy_https <proxy_address>:<proxy_port>
开放本地端口
- 打开防火墙与网络保护点击高级设置

- 新建入站规则

- 选择新建端口就好,后面一路往下,后面都直接下一步就好,就完成了。

、

第三步验证
成功

相关文章:

关于内网服务器依托可上网电脑实现访问互联网
关于内网服务器依托可上网电脑实现访问互联网 背景:在实验室内网的一个服务器,没有配置 NAT ,无法使用外网,只能在局域网内进行访问,但是呢,我们自己的电脑是可以访问互联网的,那么怎么通过让自…...

期权懂|期权入门知识:如何选择期权合约?
锦鲤三三每日分享期权知识,帮助期权新手及时有效地掌握即市趋势与新资讯! 期权入门知识:如何选择期权合约? 一、选择月份: 通常情况下,月份的选择与期货合约的选择类似,主要关注主力合约。主力…...

如何用gpt来分析链接里面的内容(比如分析论文链接)和分析包含多个文件中的一块代码
如何用gpt来分析链接里面的内容,方法如下 这里使用gpt4里面有一个网路的功能 点击搜索框下面这个地球的形状即可启动搜索网页模式 然后即可提出问题在搜索框里:发现正确识别和分析了链接里面的内容 链接如下:https://arxiv.org/pdf/2009.1…...

Bash 脚本教程
注:本文为 “Bash 脚本编写” 相关文章合辑。 BASH 脚本编写教程 as good as well于 2017-08-04 22:04:28 发布 这里有个老 American 写的 BASH 脚本编写教程,非常不错,至少没接触过 BASH 的也能看懂! 建立一个脚本 Linux 中有…...
)
Pinia最简单使用(vite+vue3)
文章目录 创建项目安装Pinia包main.js注册Pinia在src下创建store/store.js文件,放入以下内容在app.vue中的使用(在其他组件也一样的) 创建项目 npm create vitelatest my-vue-app选vue 选JavaScript cd my-vue-app npm install npm run dev安装Pinia包 npm install piniamain…...

计算机网络——期末复习(4)协议或技术汇总、思维导图
思维导图 协议与技术 物理层通信协议:曼彻斯特编码链路层通信协议:CSMA/CD (1)停止-等待协议(属于自动请求重传ARQ协议):确认、否认、重传、超时重传、 (2)回退N帧协…...

Microsoft word@【标题样式】应用不生效(主要表现为在导航窗格不显示)
背景 随笔。Microsoft word 2013基础使用,仅做参考和积累。 问题 Microsoft word 2013,对段落标题文字应用【标题样式】不生效(主要表现为在导航窗格不显示)。 图1 图2 观察图1和图2,发现图1的文字在应用【标题一】样…...

轮播图带详情插件、uniApp插件
超级好用的轮播图 介绍访问地址参数介绍使用方法(简单使用,参数结构点击链接查看详情)图片展示 介绍 带有底部物品介绍以及价格的轮播图组件,持续维护,uniApp插件,直接下载填充数据就可以在项目里面使用 …...

云计算时代携程的网络架构变迁
大家觉得有意义和帮助记得及时关注和点赞!!! 前言0 携程云平台简介 网络演进时间线1 基于 VLAN 的二层网络 1.1 需求1.2 解决方案:OpenStack Provider Network 模型1.3 硬件网络拓扑1.4 宿主机内部网络拓扑1.5 小结 优点缺点2 基于 SDN 的大二层网络 2.1 面临的新问…...

USB 状态机及状态转换
文章目录 USB 状态机及状态转换连接状态供电状态默认状态地址状态配置状态挂起状态USB 状态机及状态转换 枚举完成之前,USB 设备要经过一系列的状态变化,才能最终完成枚举。这些状态是 连接状态 - attached供电状态 - powered默认状态 - default地址状态 - address配置状态 -…...

Go C编程 第6课 无人机 --- 计算旋转角
旋转的秘密---认识角度 rt、lt命令学习 goc电子课程 一、编程步骤 第一步 第二步 第三步 第四步 二、画“四轴无人机” (一)、画第一根机轴 (二)、画第二根机轴 (三)、画完整的无人机 三、画“多轴无人…...

C++-----图
一、图的结构 在 C 中,图可以用多种结构表示,常见的有邻接矩阵和邻接表。 邻接矩阵 使用二维数组 adjMatrix 来表示图中顶点之间的连接关系。对于无向图,如果 adjMatrix[i][j] 不为零,则表示顶点 i 和顶点 j 之间存在边&#x…...

mysql 数据库迁移到达梦数据库
1.windows安装达梦数据库,去官网下载 dm8 进行安装,安装后,可以使用管理工具管理数据 使用迁移工具对数据进行迁移; 2.使用php 或者 thinkphp连接达梦数据库 2.1、先PHP开启DM扩展 从达梦数据库安装目录下drivers/php_pdo 复制对…...

【记录】使用R2 CDN替换本地项目图片以加速图片加载
将图片存储到 Cloudflare 的存储桶中,并通过其提供的公共 URL 来替换代码中的本地路径,可以减小项目中打包的图片文件体积 实现方法的详细步骤: 1. 上传图片到 Cloudflare 的存储桶 (1)登录 Cloudflare Dashboard&am…...

12.13[java exp4][debug]nginx 500,究极未解之谜,出自重启,解决自重启,迷???
pro1 pro2?????????未解之谜,究极未解之谜???? 就是 auth_request http://auth_server/auth/check;接受不到,auth_server无法受到请求,就完全没收到?但是/auth/login等直接…...

Disruptor 高性能环形消息框架
官方文档:Disruptor 1. 简介 Disruptor是一个高性能的互进程(Inter-process)和多线程(Multi-threaded)消息处理库,由LMAX交易所开发,用于在Java虚拟机(JVM)上实现高性能…...
)
Python列表(二)
方式三: 创建对应的枚举对象 概念:通过枚举函数,生成一个新的对象 作用:函数用于将一个可遍历的数据对象(如列表、元组或字符串)组合为一个索引序列 同时列出数据下标和数据 #生成枚举对象 values [&…...

计算机网络:应用层 —— 网络应用模式
文章目录 客户—服务器方式和对等方式客户/服务器方式 (C/S方式)工作流程特点 对等方式 (P2P方式)工作流程P2P 应用特点 客户—服务器方式和对等方式 网络应用程序运行在处于网络边缘的不同的端系统上,通过彼此间的通信来共同完成某项任务。 开发一种新的网络应用…...

@Repository注解和@mapper的区别
1. Repository 注解 通俗解释: 你可以把 Repository 注解想象成是一个专门负责管理数据库操作的 “仓库管理员”。这个管理员主要负责和数据库打交道,就像管理一个大仓库一样,他会进行各种操作,比如把货物(数据&#x…...

解锁成长密码:探寻刻意练习之道
刻意练习,真有那么神? 在生活中,你是否有过这样的困惑:每天苦练英语口语,可一到交流时还是支支吾吾;埋头苦学吉他,却总是卡在几个和弦转换上;工作多年,业务能力却似乎陷入…...

Python爬虫实战:研究MechanicalSoup库相关技术
一、MechanicalSoup 库概述 1.1 库简介 MechanicalSoup 是一个 Python 库,专为自动化交互网站而设计。它结合了 requests 的 HTTP 请求能力和 BeautifulSoup 的 HTML 解析能力,提供了直观的 API,让我们可以像人类用户一样浏览网页、填写表单和提交请求。 1.2 主要功能特点…...

从零实现STL哈希容器:unordered_map/unordered_set封装详解
本篇文章是对C学习的STL哈希容器自主实现部分的学习分享 希望也能为你带来些帮助~ 那咱们废话不多说,直接开始吧! 一、源码结构分析 1. SGISTL30实现剖析 // hash_set核心结构 template <class Value, class HashFcn, ...> class hash_set {ty…...

NLP学习路线图(二十三):长短期记忆网络(LSTM)
在自然语言处理(NLP)领域,我们时刻面临着处理序列数据的核心挑战。无论是理解句子的结构、分析文本的情感,还是实现语言的翻译,都需要模型能够捕捉词语之间依时序产生的复杂依赖关系。传统的神经网络结构在处理这种序列依赖时显得力不从心,而循环神经网络(RNN) 曾被视为…...

论文阅读笔记——Muffin: Testing Deep Learning Libraries via Neural Architecture Fuzzing
Muffin 论文 现有方法 CRADLE 和 LEMON,依赖模型推理阶段输出进行差分测试,但在训练阶段是不可行的,因为训练阶段直到最后才有固定输出,中间过程是不断变化的。API 库覆盖低,因为各个 API 都是在各种具体场景下使用。…...

关于easyexcel动态下拉选问题处理
前些日子突然碰到一个问题,说是客户的导入文件模版想支持部分导入内容的下拉选,于是我就找了easyexcel官网寻找解决方案,并没有找到合适的方案,没办法只能自己动手并分享出来,针对Java生成Excel下拉菜单时因选项过多导…...

Chrome 浏览器前端与客户端双向通信实战
Chrome 前端(即页面 JS / Web UI)与客户端(C 后端)的交互机制,是 Chromium 架构中非常核心的一环。下面我将按常见场景,从通道、流程、技术栈几个角度做一套完整的分析,特别适合你这种在分析和改…...

提升移动端网页调试效率:WebDebugX 与常见工具组合实践
在日常移动端开发中,网页调试始终是一个高频但又极具挑战的环节。尤其在面对 iOS 与 Android 的混合技术栈、各种设备差异化行为时,开发者迫切需要一套高效、可靠且跨平台的调试方案。过去,我们或多或少使用过 Chrome DevTools、Remote Debug…...
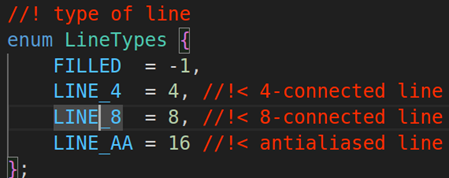
OPENCV图形计算面积、弧长API讲解(1)
一.OPENCV图形面积、弧长计算的API介绍 之前我们已经把图形轮廓的检测、画框等功能讲解了一遍。那今天我们主要结合轮廓检测的API去计算图形的面积,这些面积可以是矩形、圆形等等。图形面积计算和弧长计算常用于车辆识别、桥梁识别等重要功能,常用的API…...
智警杯备赛--excel模块
数据透视与图表制作 创建步骤 创建 1.在Excel的插入或者数据标签页下找到数据透视表的按钮 2.将数据放进“请选择单元格区域“中,点击确定 这是最终结果,但是由于环境启不了,这里用的是自己的excel,真实的环境中的excel根据实训…...

AT模式下的全局锁冲突如何解决?
一、全局锁冲突解决方案 1. 业务层重试机制(推荐方案) Service public class OrderService {GlobalTransactionalRetryable(maxAttempts 3, backoff Backoff(delay 100))public void createOrder(OrderDTO order) {// 库存扣减(自动加全…...

