机器学习之KNN算法预测数据和数据可视化
机器学习及KNN算法
目录
- 机器学习及KNN算法
- 机器学习基本概念
- 概念理解
- 步骤
- 为什么要学习机器学习
- 需要准备的库
- KNN算法
- 概念
- 算法导入
- 常用距离公式
- 算法优缺点
- 优点:
- 缺点︰
- 数据可视化
- 二维界面
- 三维界面
- KNeighborsClassifier 和KNeighborsRegressor理解
- 查看KNeighborsRegressor函数参数定义
- 查看 KNeighborsClassifier函数参数定义
- 参数理解
- 使用格式
- 预测类别实际应用
- 问题
- 特征数据
- 类别标签
- 问题理解
- 可视化数据理解
- 数据预测
- 预测数值实际应用
机器学习基本概念
概念理解
利用数学中的公式 总结出数据中的规律。
步骤
- 数据收集
数据量越大,最终训练的结果越正确 - 建立数学模型训练
针对不同的数据类型需要选择不同的数学模型 - 预测
预测数据
为什么要学习机器学习
- 信息爆炸时代,数据量太大,人工已经无法处理。
- 重复性的工作交给电脑来做。
- 潜在一些信息之间的关联人类不容易直接发现。
- 机器学习确实有效的解决很多问题。
等…
需要准备的库
- numpy
- scipy
- matplotlib
- pandas
- sklearn
Sklearn (Scikit-Learn) 是基于 Python 语言的第三方机器学习库。它建立在 NumPy, SciPy, Pandas 和 Matplotlib库 之上,里面的 API 的设计非常好,所有对象的接口简单,很适合新手上路。我使用的是1.0.2版本,可在终端下载
代码展示:
未修改pip下载源的,后面需添加 -i 镜像源地址
pip install scikit_learn==1.0.2
KNN算法
概念
全称是k-nearest neighbors,通过寻找k个距离最近的数据,来确定当前数据值的大小或类别。是机器学习中最为简单和经典的一个算法。
如果求得是值,则求其平均值为结果,如果是确定类别,则比较多的类别为结果。
算法导入
- KNeighborsClassifier 预测类别
- KNeighborsRegressor 预测值
from sklearn.neighbors import KNeighborsClassifier
from sklearn.neighbors import KNeighborsRegressor
常用距离公式
-
欧式距离:
- 二维空间:a点为(x1,y1),b点为(x2,y2)

- 三维空间:a点为(x1,y1 ,z1),b点为(x2,y2 ,z2)

- n维空间:a点为(x11,x12 ,…,x1n),b点为(x21,x22,…,x2n)

- 二维空间:a点为(x1,y1),b点为(x2,y2)
-
曼哈顿距离:
-
二维空间:a点为(x1,y1),b点为(x2,y2)

-
n维空间:a点为(x11,x12 ,…,x1n),b点为(x21,x22,…,x2n)

-
算法优缺点
优点:
1.简单,易于理解,易于实现,无需训练;
2.适合对稀有事件进行分类;
3.对异常值不敏感。
缺点︰
1.样本容量比较大时,计算时间很长;
⒉.不均衡样本效果较差;
数据可视化
二维界面
格式:
- figure(“窗口名”)
创建空白画板 - axes()
确认维度,默认二维 - scatter(x,y,c=“十六进制颜色值”,marker=“标识图案”)
设置为散点图,同时确认数据及数据显示颜色和标识图案,x,y可以是数值也可以是数组 - set(xlabel=“x”,ylabel=“y”)
设置坐标轴名称,x,y可以改为需要的坐标轴名
代码展示:
import matplotlib.pyplot as plt
a = [1,2,3,4]
# 建立空白画板
fig = plt.figure("二维")
#确认维度,默认二维
b = plt.axes()
# 数据可以是数值也可以是数组
b.scatter(2,3,c="#00F5FF",marker="o")
b.scatter(a,a,c="#00FF7F",marker="*")
b.set(xlabel="x",ylabel="y")
plt.show()
运行结果:

三维界面
格式:
- figure(“窗口名”)
创建空白画板- axes(projection=“3d”)
设置三维 - scatter(x,y,z,c=“十六进制颜色值”,marker=“标识图案”)
确认数据及数据显示颜色和标识图案,x,y,z可以是数值也可以是数组
- axes(projection=“3d”)
- set(xlabel=“x”,ylabel=“y”,zlabel=“z”)
设置坐标轴名称,x,y,z可以改为需要的坐标轴名
代码展示:
a = [1,2,3,4]
data = np.loadtxt('dating_TS.txt')
figure = plt.figure("三维")
b = plt.axes(projection="3d")
b.scatter(2,3,4,c="#00F5FF",marker="o")
b.scatter(a,a,a,c="#00FF7F",marker="*")
b.set(xlabel="x",ylabel="y",zlabel="z")
plt.show()
运行结果:

KNeighborsClassifier 和KNeighborsRegressor理解
查看KNeighborsRegressor函数参数定义
按住CTRL,鼠标点击函数可自动跳转
部分代码展示:
def __init__(self,n_neighbors=5,*,weights="uniform",algorithm="auto",leaf_size=30,p=2,metric="minkowski",metric_params=None,n_jobs=None,)
查看 KNeighborsClassifier函数参数定义
部分代码展示:
def __init__(self,n_neighbors=5,*,weights="uniform",algorithm="auto",leaf_size=30,p=2,metric="minkowski",metric_params=None,n_jobs=None,)
参数理解
- n_neighbors
k值,邻居的个数,默认为5。【关键参数】 - weights : 权重项,默认uniform方法。
- Uniform:所有最近邻样本的权重都一样。【一般使用这一个】
- Distance:权重和距离呈反比,距离越近的样本具有更高的权重。【确认样本分布情况,混乱使用这种形式】
- Callable:用户自定义权重。
- algorithm :用于计算最近邻的算法。
- ball_tree:球树实现
- kd_tree:KD树实现, 是一种对n维空间中的实例点进行存储以便对其进行快速搜索的二叉树结构。
- brute:暴力实现
- auto:自动选择,权衡上述三种算法。【一般按自动即可】
leaf_size :空值KD树或者球树的参数,停止建子树的叶子节点的阈值。
- p : 距离的计算方式。P=1为曼哈顿距离,p=2为欧式距离。
1.曼哈顿距离2.欧式距离3.切比雪夫距离4.闵可夫斯基距离5.带权重闵可夫斯基距离
6.标准化欧式距离7.马氏距离 - metric : 用于树的距离度量
“euclidean” EuclideanDistance -sqrt(sum((x - y)^2))
“manhattan” ManhattanDistance -sum(|x - y|)
“chebyshev” ChebyshevDistance -max(|x - y|)
“minkowski” MinkowskiDistance p, wsum(w * |x - y|^p)^(1/p)
“wminkowski” WMinkowskiDistance p, wsum(|w * (x - y)|^p)^(1/p)
“seuclidean” SEuclideanDistance Vsqrt(sum((x - y)^2 / V))
“mahalanobis” MahalanobisDistance V or VI ``sqrt((x - y)’ V^-1 (x - y)) - metric_params :用于比较复杂的距离的度量附加参数。【用不上】
使用格式
- x = data1 特征数据
- y = data2 结果(平均值/较多类别)
- n = KNeighborsClassifier(n_neighbors=7,p=1,metric=“euclidean”)
确定最近个数为7,和距离计算方式1曼哈顿距离,树的距离方式是欧式距离 - n.fit(x,y)
自带的训练模型,自动按上方设置计算判断 - n.predict(二维数组)
预测二维数组的结果
预测类别实际应用
问题
现在有很多大学里出现室友矛盾,假如室友可以选择: 大学里面 ,对于校方,把类型相同的学生放在一个寝室,在基于大二大三大四的,现已存在一个数据文件datingTestSet2.txt ,为历年大学生的调查问卷表。
特征数据
第1列:每年旅行的路程
第2列:玩游戏所有时间百分比
第3列:每个礼拜消 零食
类别标签
1表示爱学习,2表示一般般,3表示爱玩,目的为学生在大学中挑选室友的信息
datingTestSet2.txt 部分数据展示:

问题理解
根据最近距离的k个距离最近的类别标签来预测要确定如有[1500,0.924729,0.2134935]特征数据的学生的类别标签,进而分寝室。
注意点:最近距离是由三列特征数据来计算,结果是类别,需要使用的是KNeighborsClassifier
可视化数据理解
data[:,-1] 索引数据最后一列
data[:,-1] ==1 判断为类别1为T,否则为F,结果是bool值
data[data[:,-1]==1] 根据判断归类各个类别数据
data_1[:,0],data_1[:,1],data_1[:,2] 分别为第1,2,3列特征数据
由颜色表示类别3种
调试查看数据data

data[:,-1]

data[:,-1] ==1

data[data[:,-1]==1]

代码展示:
import numpy as np
import matplotlib.pyplot as plt
from sklearn.neighbors import KNeighborsRegressor
data = np.loadtxt('dating_TS.txt')
data_1 = data[data[:,-1]==1]
data_2 = data[data[:,-1]==2]
data_3 = data[data[:,-1]==3]
a_d = data[:,-1]
a_d_1 = [data[:,-1]==1]
fig = plt.figure()
a = plt.axes(projection="3d")
a.scatter(data_1[:,0],data_1[:,1],data_1[:,2],c="#00F5FF",marker="o")
a.scatter(data_2[:,0],data_2[:,1],data_2[:,2],c="#00FF7F",marker="o")
a.scatter(data_3[:,0],data_3[:,1],data_3[:,2],c="#000080",marker="o")
a.set(xlabel="x",ylabel="y",zlabel="z")
plt.show()
运行结果:

数据预测
代码展示:
import numpy as np
import matplotlib.pyplot as plt
from sklearn.neighbors import KNeighborsClassifier
from sklearn.neighbors import KNeighborsRegressor
data = np.loadtxt('dating_TS.txt')
x = data[: , :-1]
y = data[: , -1]
n = KNeighborsClassifier(n_neighbors=7,p=1)
n.fit(x,y)
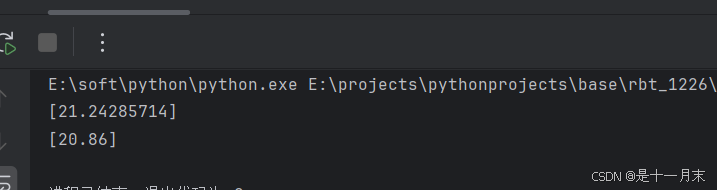
print(n.predict([[1500,0.924729,0.2134935]]))
p_data = [[1234,2.4567,0.5467],[123435,8.2134,2.345],[5668,3.6754,0.34567]
]
print(n.predict(p_data))
n1 = KNeighborsClassifier(n_neighbors=3,p=2,metric="euclidean")
n1.fit(x,y)
print(n1.predict([[1500,0.924729,0.2134935]]))
p_data = [[1234,2.4567,0.5467],[123435,8.2134,2.345],[5668,3.6754,0.34567]
]
print(n1.predict(p_data))
运行结果:

预测数值实际应用
给定房屋特征和价格数据,最后一列为价格,来根据历史数据预测价格
部分房屋特征和价格数据展示:

代码展示:
import numpy as np
from sklearn.neighbors import KNeighborsRegressor
data_f = np.loadtxt('data_f1.txt')
x = data_f[:,:-1]
y = data_f[:,-1]
n = KNeighborsRegressor(n_neighbors=7,p=2,metric="euclidean")
n.fit(x,y)
print(n.predict([[ 2.82838,0.00,18.120,0,0.5320,5.7620,40.32,4.0983,24,666.0,20.21,392.93,10.42]]))
n1 = KNeighborsRegressor(n_neighbors=5,p=2,metric="euclidean")
n1.fit(x,y)
print(n1.predict([[ 2.82838,0.00,18.120,0,0.5320,5.7620,40.32,4.0983,24, 666.0,20.21,392.93,10.42]]))
运行结果:
相关文章:

机器学习之KNN算法预测数据和数据可视化
机器学习及KNN算法 目录 机器学习及KNN算法机器学习基本概念概念理解步骤为什么要学习机器学习需要准备的库 KNN算法概念算法导入常用距离公式算法优缺点优点:缺点︰ 数据可视化二维界面三维界面 KNeighborsClassifier 和KNeighborsRegressor理解查看KNeighborsRegr…...
前端node.js
一.什么是node.js 官网解释:Node.js 是一个开源的、跨平台的 JavaScript 运行时环境。 二.初步使用node.js 需要区分开的是node.js和javascript互通的只有console和定时器两个API. 三.Buffer Buffer 是一个类似于数组的对象,用于表示固定长度的字节序列。 Buffer…...
Excel基础知识
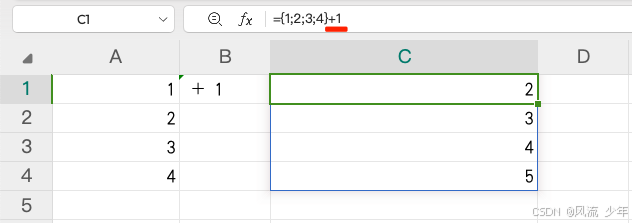
一:数组 一行或者一列数据称为一维数组,多行多列称为二维数组,数组支持算术运算(如加减乘除等)。 行:{1,2,3,4} 数组中的每个值用逗号分隔列:{1;2;3;4} 数组中的每个值用分号分隔行列…...

Spring Boot对访问密钥加密解密——RSA
场景 用户无需登录,仅仅根据给定的访问keyId和keySecret就可以访问接口。 keyId 等可以明文发送(不涉及机密),后端直接从请求头读取。keySecret 不可明文,需要加密后放在另一个请求头(或请求体࿰…...

Vue介绍
一、Vue框架简介 Vue.js是一个用于构建用户界面的渐进式JavaScript框架。它的核心库只关注视图层,易于上手,并且可以与其他库或现有项目进行整合。其特点包括响应式数据绑定、组件化开发和虚拟DOM等。 响应式数据绑定 Vue通过Object.defineProperty()方法来进行数据劫持。当…...
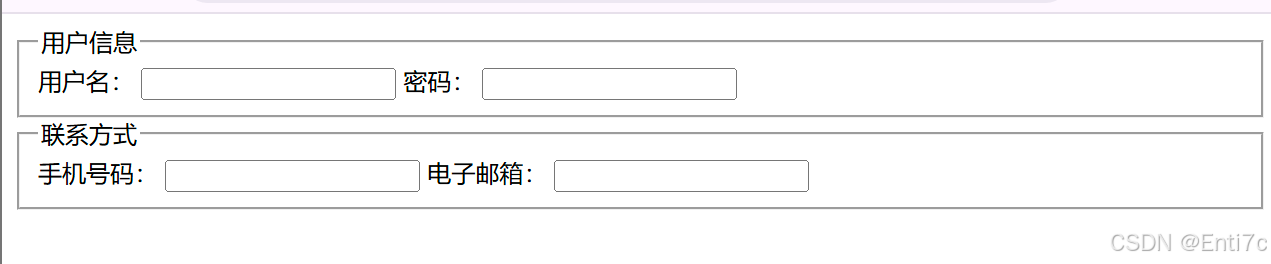
表单元素(标签)有哪些?
HTML 中的表单元素(标签)用于收集用户输入的数据,常见的有以下几种: 文本输入框 <input type"text">:用于单行文本输入,如用户名、密码等。可以通过设置maxlength属性限制输入字符数&…...
人工智能与云计算的结合:如何释放数据的无限潜力?
引言:数据时代的契机 在当今数字化社会,数据已成为推动经济与技术发展的核心资源,被誉为“21世纪的石油”。从个人消费行为到企业运营决策,再到城市管理与国家治理,每个环节都在生成和积累海量数据。然而,数…...

TCP Analysis Flags 之 TCP Out-Of-Order
前言 默认情况下,Wireshark 的 TCP 解析器会跟踪每个 TCP 会话的状态,并在检测到问题或潜在问题时提供额外的信息。在第一次打开捕获文件时,会对每个 TCP 数据包进行一次分析,数据包按照它们在数据包列表中出现的顺序进行处理。可…...

【MyBatis 核心工作机制】注解式开发与动态代理原理
有很多朋友可能已经在开发中熟练使用 MyBatis 或者刚开始学习 MyBatis,对于它的一些工作机制不太了解。“咦,怎么写几个注解,写几个配置文件,就能实现这些效果呢,好神奇呀!”当你看完这篇博客之后…...

深度学习在图像识别中的最新进展与实践案例
深度学习在图像识别中的最新进展与实践案例 在当今信息爆炸的时代,图像作为信息传递的重要载体,其处理与分析技术显得尤为重要。深度学习,作为人工智能领域的一个分支,凭借其强大的特征提取与模式识别能力,在图像识别…...

vue3中如何自定义插件
英译汉插件 i18n.ts export default {install: (app: any, options: any) > {// 注入一个全局可用的$translate()方法app.config.globalProperties.$translate (key: string) > {// 获取options对象的深层属性// 使用key作为索引return key.split(".").redu…...

【机器学习】回归
文章目录 1. 如何训练回归问题2. 泛化能力3. 误差来源4. 正则化5. 交叉验证 1. 如何训练回归问题 第一步:定义模型 线性模型: y ^ b ∑ j w j x j \hat{y} b \sum_{j} w_j x_j y^b∑jwjxj 其中,( w ) 是权重,( b )…...
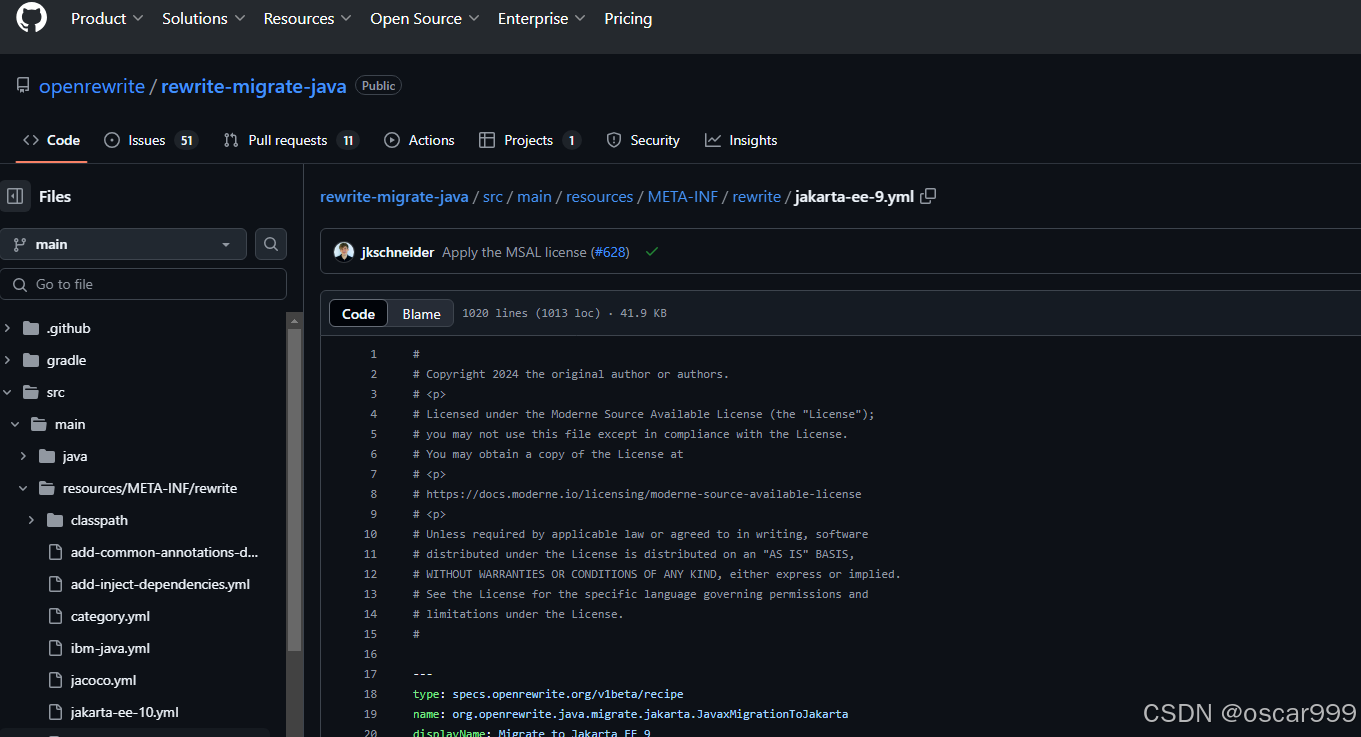
Maven项目中不修改 pom.xml 状况下直接运行OpenRewrite的配方
在Java 的Maven项目中,可以在pom.xml 中配置插件用来运行OpenRewrite的Recipe,但是有一些场景是希望不修改pom.xml 文件就可以运行Recipe,比如: 因为不需要经常运行 OpenRewrite,所以不想在pom.xml 加入不常使用的插件…...

【翻译】Sora 系统卡-12月9日
Sora System ard | OpenAI 简介 Sora 概述 Sora 是 OpenAI 的视频生成模型,旨在接收文本、图像和视频输入并生成新视频作为输出。用户可以创建各种格式的分辨率高达 1080p(最长 20 秒)的视频,从文本生成新内容,或增强…...
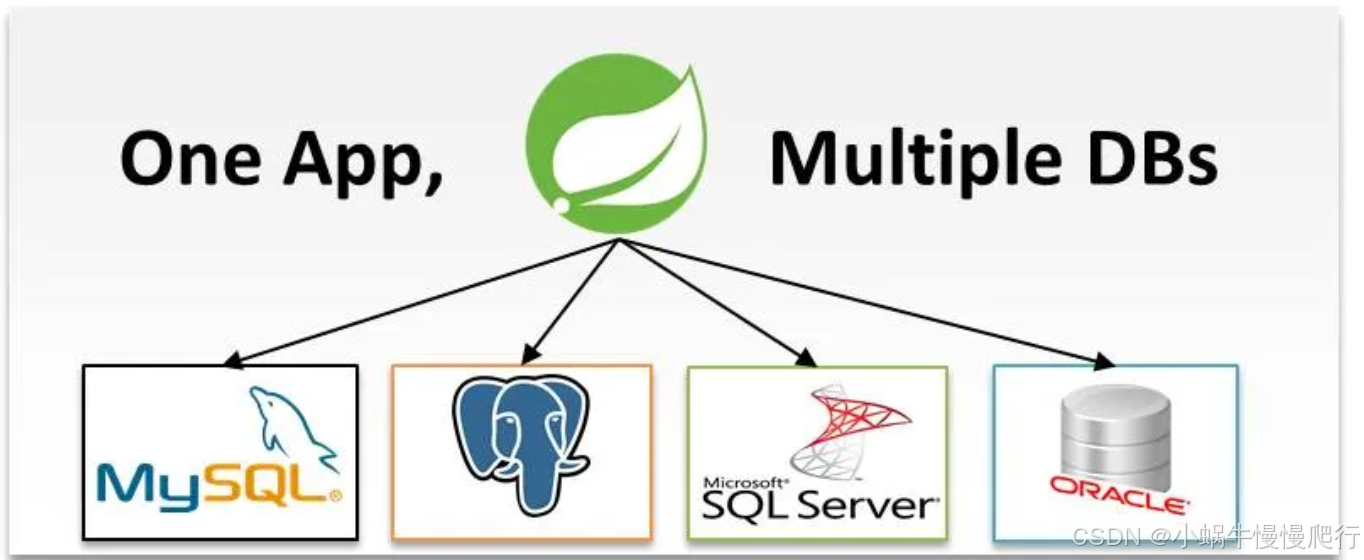
如何在 Spring Boot 微服务中设置和管理多个数据库
在现代微服务架构中,通常需要与多个数据库交互的服务。这可能是由于各种原因,例如遗留系统集成、不同类型的数据存储需求,或者仅仅是为了优化性能。Spring Boot 具有灵活的配置和强大的数据访问库,可以轻松配置多个数据库。在本综…...
Ubuntu20.04安装Foxit Reader 福昕阅读器
Ubuntu20.04安装Foxit Reader 福昕阅读器 文章目录 Ubuntu20.04安装Foxit Reader 福昕阅读器 先更新一下源 sudo apt update sudo apt upgrade下载Foxit Reader的稳定版本 wget https://cdn01.foxitsoftware.com/pub/foxit/reader/desktop/linux/2.x/2.4/en_us/FoxitReader.e…...

学习threejs,THREE.CircleGeometry 二维平面圆形几何体
👨⚕️ 主页: gis分享者 👨⚕️ 感谢各位大佬 点赞👍 收藏⭐ 留言📝 加关注✅! 👨⚕️ 收录于专栏:threejs gis工程师 文章目录 一、🍀前言1.1 ☘️THREE.CircleGeometry 圆形…...

Tonghttpserver6.0.1.3 使用整理(by lqw)
文章目录 1.声明2.关于单机版控制台和集中管理控制台3.单机版控制台3.1安装,启动和查看授权信息3.2一些常见的使用问题(单机控制台)3.3之前使用的是nginx,现在要配nginx.conf上的配置,在THS上如何配置3.4如何配置密码过…...

redis开发与运维-redis0401-补充-redis流水线与Jedis执行流水线
文章目录 【README】【1】redis流水线Pipeline【1.1】redis流水线概念【1.2】redis流水线性能测试【1.2.1】使用流水线与未使用流水线的性能对比【1.2.2】使用流水线与redis原生批量命令的性能对比【1.2.3】流水线缺点 【1.3】Jedis客户端执行流水线【1.3.1】Jedis客户端执行流…...

OPPO Java面试题及参考答案
Java 语言的特点 Java 是一种面向对象的编程语言,它具有以下显著特点。 首先是简单性。Java 的语法相对简单,它摒弃了 C 和 C++ 语言中一些复杂的特性,比如指针操作。这使得程序员能够更专注于业务逻辑的实现,而不是陷入复杂的语法细节中。例如,Java 的内存管理是自动进行…...

测试微信模版消息推送
进入“开发接口管理”--“公众平台测试账号”,无需申请公众账号、可在测试账号中体验并测试微信公众平台所有高级接口。 获取access_token: 自定义模版消息: 关注测试号:扫二维码关注测试号。 发送模版消息: import requests da…...

MFC内存泄露
1、泄露代码示例 void X::SetApplicationBtn() {CMFCRibbonApplicationButton* pBtn GetApplicationButton();// 获取 Ribbon Bar 指针// 创建自定义按钮CCustomRibbonAppButton* pCustomButton new CCustomRibbonAppButton();pCustomButton->SetImage(IDB_BITMAP_Jdp26)…...

23-Oracle 23 ai 区块链表(Blockchain Table)
小伙伴有没有在金融强合规的领域中遇见,必须要保持数据不可变,管理员都无法修改和留痕的要求。比如医疗的电子病历中,影像检查检验结果不可篡改行的,药品追溯过程中数据只可插入无法删除的特性需求;登录日志、修改日志…...

关于nvm与node.js
1 安装nvm 安装过程中手动修改 nvm的安装路径, 以及修改 通过nvm安装node后正在使用的node的存放目录【这句话可能难以理解,但接着往下看你就了然了】 2 修改nvm中settings.txt文件配置 nvm安装成功后,通常在该文件中会出现以下配置&…...

蓝牙 BLE 扫描面试题大全(2):进阶面试题与实战演练
前文覆盖了 BLE 扫描的基础概念与经典问题蓝牙 BLE 扫描面试题大全(1):从基础到实战的深度解析-CSDN博客,但实际面试中,企业更关注候选人对复杂场景的应对能力(如多设备并发扫描、低功耗与高发现率的平衡)和前沿技术的…...

dify打造数据可视化图表
一、概述 在日常工作和学习中,我们经常需要和数据打交道。无论是分析报告、项目展示,还是简单的数据洞察,一个清晰直观的图表,往往能胜过千言万语。 一款能让数据可视化变得超级简单的 MCP Server,由蚂蚁集团 AntV 团队…...

Pinocchio 库详解及其在足式机器人上的应用
Pinocchio 库详解及其在足式机器人上的应用 Pinocchio (Pinocchio is not only a nose) 是一个开源的 C 库,专门用于快速计算机器人模型的正向运动学、逆向运动学、雅可比矩阵、动力学和动力学导数。它主要关注效率和准确性,并提供了一个通用的框架&…...

2025季度云服务器排行榜
在全球云服务器市场,各厂商的排名和地位并非一成不变,而是由其独特的优势、战略布局和市场适应性共同决定的。以下是根据2025年市场趋势,对主要云服务器厂商在排行榜中占据重要位置的原因和优势进行深度分析: 一、全球“三巨头”…...

HarmonyOS运动开发:如何用mpchart绘制运动配速图表
##鸿蒙核心技术##运动开发##Sensor Service Kit(传感器服务)# 前言 在运动类应用中,运动数据的可视化是提升用户体验的重要环节。通过直观的图表展示运动过程中的关键数据,如配速、距离、卡路里消耗等,用户可以更清晰…...

Java求职者面试指南:Spring、Spring Boot、Spring MVC与MyBatis技术解析
Java求职者面试指南:Spring、Spring Boot、Spring MVC与MyBatis技术解析 一、第一轮基础概念问题 1. Spring框架的核心容器是什么?它的作用是什么? Spring框架的核心容器是IoC(控制反转)容器。它的主要作用是管理对…...
