LeetCode 热题 100_二叉树展开为链表(46_114_中等_C++)(二叉树;先序遍历(递归+数组);先序遍历(递归))
LeetCode 热题 100_二叉树展开为链表(46_114)
- 题目描述:
- 输入输出样例:
- 题解:
- 解题思路:
- 思路一(先序遍历(递归+数组)):
- 思路二(先序遍历(非递归)):
- 代码实现
- 代码实现(思路一(先序遍历(递归+数组))):
- 代码实现(思路二(先序遍历(非递归))):
- 以思路一为例进行调试
题目描述:
给你二叉树的根结点 root ,请你将它展开为一个单链表:
展开后的单链表应该同样使用 TreeNode ,其中 right 子指针指向链表中下一个结点,而左子指针始终为 null 。
展开后的单链表应该与二叉树 先序遍历 顺序相同。
输入输出样例:
示例 1:

输入:root = [1,2,5,3,4,null,6]
输出:[1,null,2,null,3,null,4,null,5,null,6]
示例 2:
输入:root = []
输出:[]
示例 3:
输入:root = [0]
输出:[0]
提示:
树中结点数在范围 [0, 2000] 内
-100 <= Node.val <= 100
题解:
解题思路:
思路一(先序遍历(递归+数组)):
1、在进行先序遍历的时候先将结点的信息存储到数组中,通过数组中的先后顺序更新每个结点的指向。
2、复杂度分析:
① 时间复杂度:O(n),n为二叉树中节点的个数,需遍历一遍二叉树O(n),遍历一遍数组更改指针的指向O(n)。
② 空间复杂度:O(n),递归遍历所需空间最多为O(n),一个额外的数组存储二叉树的信息O(n)。
思路二(先序遍历(非递归)):
1、如果我们采用非递归的方式,当我们遍历到一个结点时,我们就可以用一个指针来记录先序遍历中上一个结点的信息,通过修改上一个结点的指向来转换成单链表。
3、复杂度分析
① 时间复杂度:O(n),n为二叉树中节点的个数,需遍历一遍二叉树O(n)。
② 空间复杂度:O(n),先序遍历的非递归实现需要借助栈实现,最坏情况下栈中有n个结点信息。
代码实现
代码实现(思路一(先序遍历(递归+数组))):
//方法一(递归):采用递归的前序遍历将遍历的结点存储在数组中,然后修改指针的指向
void flatten1(TreeNode* root) {//nums_TreeNode存放先序遍历各节点的顺序vector<TreeNode *>nums_TreeNode;//先序遍历将结点信息存储在nums_TreeNode中preorder(root,nums_TreeNode);//根据nums_TreeNode中结点的顺序更改结点的指向for (int i = 1; i < nums_TreeNode.size(); i++){nums_TreeNode[i-1]->left=nullptr;nums_TreeNode[i-1]->right=nums_TreeNode[i];}
}//先序遍历将结点信息存储在nums_TreeNode中
//注意vector<TreeNode *>&nums_TreeNode这里的引用(&)
void preorder(TreeNode *root,vector<TreeNode *>&nums_TreeNode){if(root==nullptr) return;nums_TreeNode.emplace_back(root);preorder(root->left,nums_TreeNode);preorder(root->right,nums_TreeNode);
}
代码实现(思路二(先序遍历(非递归))):
//方法二:非递归先序遍历,pre代表当前遍历结点的前一个结点,改变pre左右孩子结点的指向
void flatten2(TreeNode* root) {if(root==nullptr) return ;stack<TreeNode *>stk;stk.push(root);//存放展开单链表的末尾TreeNode *tail=nullptr;while (!stk.empty()){TreeNode *node=stk.top();stk.pop();//更改结点的指向if(tail!=nullptr) {tail->left=nullptr;tail->right=node;}//注意右子结点先入栈if(node->right!=nullptr) stk.push(node->right);if(node->left!=nullptr) stk.push(node->left);//更新单链表的尾结点tail=node;}
}
以思路一为例进行调试
#include<iostream>
#include<vector>
#include<queue>
#include<stack>
using namespace std;struct TreeNode
{int val;TreeNode *left;TreeNode *right;TreeNode():val(0),left(nullptr),right(nullptr){}TreeNode(int val):val(val),left(nullptr),right(nullptr){}TreeNode(int val,TreeNode *left,TreeNode *right):val(val),left(left),right(right){}
};//通过数组创建二叉树,数组中-1代表nullptr
TreeNode *createTree(vector <int> nums){if (nums.empty()) return nullptr;TreeNode *root=new TreeNode(nums[0]);queue<TreeNode *> q;q.push(root);int i=1;while (i<nums.size()){//注意这里不能用root,会改变root的指向TreeNode *node=q.front();q.pop();if(i<nums.size()&&nums[i]!=-1){node->left=new TreeNode(nums[i]);q.push(node->left);}++i;if(i<nums.size()&&nums[i]!=-1){node->right=new TreeNode(nums[i]);q.push(node->right);}++i;}return root;
}//中序遍历输出二叉树,用于验证二叉树是否创建正确
void inorder_Traversal(TreeNode *root){if(root==nullptr) return; inorder_Traversal(root->left);cout<<root->val<<" ";inorder_Traversal(root->right);
}class Solution
{
public://方法一(递归):采用递归的前序遍历将遍历的结点存储在数组中,然后修改指针的指向void flatten1(TreeNode* root) {vector<TreeNode *>nums_TreeNode;preorder(root,nums_TreeNode);for (int i = 1; i < nums_TreeNode.size(); i++){nums_TreeNode[i-1]->left=nullptr;nums_TreeNode[i-1]->right=nums_TreeNode[i];}}//注意vector<TreeNode *>&nums_TreeNode这里的引用(&)void preorder(TreeNode *root,vector<TreeNode *>&nums_TreeNode){if(root==nullptr) return;nums_TreeNode.emplace_back(root);preorder(root->left,nums_TreeNode);preorder(root->right,nums_TreeNode);}
};int main(){vector<int> nums={1,2,5,3,4,-1,6};//通过数组创建二叉树,-1为nullptrTreeNode* root=createTree(nums);//测试二叉树是否创建正确//inorder_Traversal(root);//二叉树展开为链表Solution s;s.flatten2(root);//输出转换的单链表while (root!=nullptr){cout<<root->val<<"->";root=root->right;}cout<<"nullptr";return 0;
}LeetCode 热题 100_二叉树展开为链表(46_114)原题链接
欢迎大家和我沟通交流(✿◠‿◠)
相关文章:

LeetCode 热题 100_二叉树展开为链表(46_114_中等_C++)(二叉树;先序遍历(递归+数组);先序遍历(递归))
LeetCode 热题 100_二叉树展开为链表(46_114) 题目描述:输入输出样例:题解:解题思路:思路一(先序遍历(递归数组)):思路二(先序遍历&am…...

uniapp实现在card卡片组件内为图片添加长按保存、识别二维码等功能
在原card组件的cover属性添加图片的话,无法在图片上面绑定 show-menu-by-longpress"true"属性,通过将图片自定义添加可使用该属性。 代码: <uni-card title"标题" padding"10px 0" :thumbnail"avata…...

最好用的图文识别OCR -- PaddleOCR(2) 提高推理效率(PPOCR模型转ONNX模型进行推理)
在实际推理过程中,使用 PaddleOCR 模型时效率较慢,经测试每张图片的检测与识别平均耗时超过 5 秒,这在需要大规模自动化处理的场景中无法满足需求。为此,我尝试将 PaddleOCR 模型转换为 ONNX 格式进行推理,以提升效率。…...

Redis--20--大Key问题解析
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 大Key问题1.什么是 Redis 大 Key?在 Redis 中,大 Key 是指单个键值对的数据量非常大,可能包含大量数据。 2. Redis大Key的危害3.…...

新版2024AndroidStudio项目目录结构拆分
如题 下载了最新版的android studio 发现目录结构和以前不一样 自动帮你合并了 如何层层抽丝剥茧呢 按照一下步骤即可解决问题!...

STM32内置Flash
一、原理 利用flash存储用户数据需要注意查看,用户数据是否会覆盖芯片运行程序。 IAP(在程序中编程)利用程序修改程序本身,和OTA是一个原理。IAP在程序中编程支持任意一种通信下载。 ICP(在电路中编程,通…...

华为路由器、交换机、AC、新版本开局远程登录那些坑(Telnet、SSH/HTTP避坑指南)
关于华为设备远程登录配置开启的通用习惯1、HTTP/HTTPS相关服务 http secure-server enablehttp server enable 2、Telnet服务telnet server enable3、SSH服务stelnet server enablessh user admin authentication-type password 「模拟器、工具合集」复制整段内容 链接&…...

【Linux】深入理解进程信号机制:信号的产生、捕获与阻塞
🎬 个人主页:谁在夜里看海. 📖 个人专栏:《C系列》《Linux系列》《算法系列》 ⛰️ 时间不语,却回答了所有问题 目录 📚前言 📚一、信号的本质 📖1.异步通信 📖2.信…...

前端基础技术全解析:从HTML前端基础标签语言开始,逐步深入CSS样式修饰、JavaScript脚本控制、Ajax异步通信以及WebSocket持久通信
目录 前言: 1.前端技术html简单了解: 1.1HTML代码是由标签构成的。 1.2.HTML 文件基本结构 1.3.HTML 常见标签 标题标签: 段落标签: p 文本格式化标签 图片标签: 超链接标签: a 测试代码: 展示效果: 表单…...

Linux存储管理之核心秘密(The Core Secret of Linux Storage Management)
Linux存储管理之核心秘密 如果你来自Windows环境,那么Linux处理和管理存储设备的方式对你而言可能显得格外不同。我们知道,Linux的文件系统并不采用Windows那样的物理驱动器表示方式(如C:、D:或E:),而是构建了一个以&…...

excel精简使用工具
1.获取sheet1的行填充到sheet2的列 希望在 Excel 中使用 INDEX 函数从不同的列中提取数据,并且每一行都引用不同的列。为了实现这个目标,你可以使用 COLUMN 函数来动态获取列的偏移量。 为了避免手动输入每个单元格的公式,你可以使用以下公…...

Flutter鸿蒙化 在鸿蒙应用中添加Flutter页面
前言 今天这节课我们讲一下 在鸿蒙应用中添加Flutter页面。 作用: 之前有很多朋友和网友问我鸿蒙能不能使用Flutter开发,他们的项目已经用Flutter开发成熟了有什么好的方案呢,今天讲到这个就可以很好的解决他们的问题,例如我们正式项目中可能是一部分native 开发 一部分…...

为什么页面无法正确显示?都有哪些HTML和CSS相关问题?
页面无法正确显示可能由多种原因导致,通常与HTML和CSS的结构、语法错误、浏览器兼容性、资源加载等问题有关。以下是一些常见的原因及其解决方法,结合实际项目代码示例进行讲解: 1. HTML 结构错误 HTML 标签的缺失或错误可能导致页面无法正…...

如何制作一份出色的公司介绍PPT?
制作一份公司介绍的PPT需要精心设计,以确保内容既专业又吸引人。以下是一个基本的框架和一些建议,帮助您创建一份有效的公司介绍PPT: PPT标题页 标题:公司全称(可使用公司Logo作为背景或嵌入标题中)副标题…...

Selenium 进行网页自动化操作的一个示例,绕过一些网站的自动化检测。python编程
这段代码是使用 Selenium 进行网页自动化操作的一个示例,主要目的是在加载网页时执行一些自定义的 JavaScript 代码,并等待页面上某个元素的出现。以下是代码的详细解释: ### 代码解释 #### 导入必要的模块 python from selenium.webdriver…...

HashMap和HashTable的区别
1、HashMap是线程不安全的,HashTable是线程安全的 HashMap:Fail-fast 机制。表示快速失败,在集合遍历过程中,一旦发现容器中的数据被修改了,会立刻抛出ConcurrentModificationException异常,从而导致遍历失…...

使用redis来进行调优有哪些方案?
Redis的调优方案可以从多个方面进行,以下是一些常见的优化方法及代码示例: 1.使用管道(Pipelining) 管道技术可以减少客户端与Redis之间的交互次数,从而提高性能。在批量操作时,通过管道可以一次性发送多个…...

macOS 中,默认的 Clang 编译器和 Homebrew 安装的 GCC 都不包含 bits/stdc++.h 文件
在 macOS 中,默认的 Clang 编译器和 Homebrew 安装的 GCC 都不包含 bits/stdc.h 文件,因为它是一个 非标准 的头文件,主要由 MinGW 和某些 Linux 平台的 GCC 提供。 解决方案 : 手动创建 bits/stdc.h 1. 创建文件夹和文件 在你的 GCC 标准…...

2012mfc,自绘列表控件
原文 使用常用控件版本4.70中的自定义绘画功能自定义列表控件的外观. 介绍 常见控件的4.70版引入了一项叫自定义绘画的功能. 可按轻量易用的自画版本对待自定义绘画.易用性来自,即只需处理一条消息(NM_CUSTOMDRAW),且你可让窗口为你干活,因此你不必完成物主绘画中的所有粗活…...

vue3运行时执行过程步骤
在 Vue 3 中,运行时的执行过程是一个复杂但高效的机制,主要包括初始化应用、渲染、响应式更新和销毁等阶段。以下是 Vue 3 运行时的执行过程的核心步骤和流程: 1. 应用初始化 1.1 创建 Vue 应用 调用 createApp 方法,创建一个 V…...

JUC笔记(上)-复习 涉及死锁 volatile synchronized CAS 原子操作
一、上下文切换 即使单核CPU也可以进行多线程执行代码,CPU会给每个线程分配CPU时间片来实现这个机制。时间片非常短,所以CPU会不断地切换线程执行,从而让我们感觉多个线程是同时执行的。时间片一般是十几毫秒(ms)。通过时间片分配算法执行。…...

大学生职业发展与就业创业指导教学评价
这里是引用 作为软工2203/2204班的学生,我们非常感谢您在《大学生职业发展与就业创业指导》课程中的悉心教导。这门课程对我们即将面临实习和就业的工科学生来说至关重要,而您认真负责的教学态度,让课程的每一部分都充满了实用价值。 尤其让我…...

C/C++ 中附加包含目录、附加库目录与附加依赖项详解
在 C/C 编程的编译和链接过程中,附加包含目录、附加库目录和附加依赖项是三个至关重要的设置,它们相互配合,确保程序能够正确引用外部资源并顺利构建。虽然在学习过程中,这些概念容易让人混淆,但深入理解它们的作用和联…...

【Linux系统】Linux环境变量:系统配置的隐形指挥官
。# Linux系列 文章目录 前言一、环境变量的概念二、常见的环境变量三、环境变量特点及其相关指令3.1 环境变量的全局性3.2、环境变量的生命周期 四、环境变量的组织方式五、C语言对环境变量的操作5.1 设置环境变量:setenv5.2 删除环境变量:unsetenv5.3 遍历所有环境…...

nnUNet V2修改网络——暴力替换网络为UNet++
更换前,要用nnUNet V2跑通所用数据集,证明nnUNet V2、数据集、运行环境等没有问题 阅读nnU-Net V2 的 U-Net结构,初步了解要修改的网络,知己知彼,修改起来才能游刃有余。 U-Net存在两个局限,一是网络的最佳深度因应用场景而异,这取决于任务的难度和可用于训练的标注数…...

Ubuntu系统多网卡多相机IP设置方法
目录 1、硬件情况 2、如何设置网卡和相机IP 2.1 万兆网卡连接交换机,交换机再连相机 2.1.1 网卡设置 2.1.2 相机设置 2.3 万兆网卡直连相机 1、硬件情况 2个网卡n个相机 电脑系统信息,系统版本:Ubuntu22.04.5 LTS;内核版本…...

【免费数据】2005-2019年我国272个地级市的旅游竞争力多指标数据(33个指标)
旅游业是一个城市的重要产业构成。旅游竞争力是一个城市竞争力的重要构成部分。一个城市的旅游竞争力反映了其在旅游市场竞争中的比较优势。 今日我们分享的是2005-2019年我国272个地级市的旅游竞争力多指标数据!该数据集源自2025年4月发表于《地理学报》的论文成果…...

webpack面试题
面试题:webpack介绍和简单使用 一、webpack(模块化打包工具)1. webpack是把项目当作一个整体,通过给定的一个主文件,webpack将从这个主文件开始找到你项目当中的所有依赖文件,使用loaders来处理它们&#x…...
C++中vector类型的介绍和使用
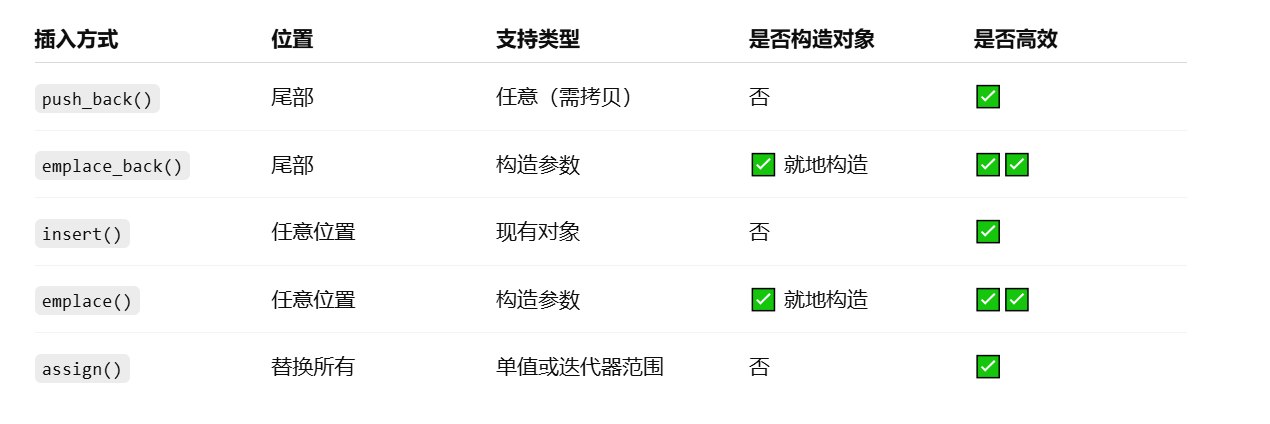
文章目录 一、vector 类型的简介1.1 基本介绍1.2 常见用法示例1.3 常见成员函数简表 二、vector 数据的插入2.1 push_back() —— 在尾部插入一个元素2.2 emplace_back() —— 在尾部“就地”构造对象2.3 insert() —— 在任意位置插入一个或多个元素2.4 emplace() —— 在任意…...

AT模式下的全局锁冲突如何解决?
一、全局锁冲突解决方案 1. 业务层重试机制(推荐方案) Service public class OrderService {GlobalTransactionalRetryable(maxAttempts 3, backoff Backoff(delay 100))public void createOrder(OrderDTO order) {// 库存扣减(自动加全…...
