Python机器学习笔记(十八、交互特征与多项式特征)
添加原始数据的交互特征(interaction feature)和多项式特征(polynomial feature)可以丰富特征表示,特别是对于线性模型。这种特征工程可以用统计建模和许多实际的机器学习应用中。
上一次学习:线性模型对wave数据集中的每个箱子都学到一个常数值。但我们知道,线性模型不仅可以学习偏移,还可以学习斜率。想要向分箱数据上的线性模型添加斜率,一种方法是重新加入原始特征。这样会得到11维的数据集,如下代码:
import numpy as np
import mglearn
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
#from sklearn.tree import DecisionTreeRegressor
#from sklearn.preprocessing import OneHotEncoder
from sklearn.preprocessing import KBinsDiscretizerX, y = mglearn.datasets.make_wave(n_samples=100)
line = np.linspace(-3, 3, 1000, endpoint=False).reshape(-1, 1)# 生成10个箱子
#kb = KBinsDiscretizer(n_bins=10, strategy='uniform')
#kb.fit(X)kb = KBinsDiscretizer(n_bins=10, strategy='uniform', encode='onehot-dense')
kb.fit(X)
#X_binned = kb.transform(X)
# 记录每个数据点所属的箱子。
X_binned = kb.transform(X)
line_binned = kb.transform(line)# 加入原始特征
X_combined = np.hstack([X, X_binned])
print(X_combined.shape)reg = LinearRegression().fit(X_combined, y)line_combined = np.hstack([line, line_binned])
plt.plot(line, reg.predict(line_combined), label='linear regression combined')
plt.vlines(kb.bin_edges_[0], -3, 3, linewidth=1, alpha=.2)
plt.legend(loc="best")
plt.ylabel("Regression output")
plt.xlabel("Input feature")
plt.plot(X[:, 0], y, 'o', c='k')
plt.show()输出结果:(100, 11)
输出图形:

输出的图形是使用分箱特征和单一全局斜率的线性回归。
在这个例子中,模型在每个箱子中都学到一个偏移,还学到一个斜率。学到的斜率是向下的,并且在所有箱子中都相同——只有一个x轴特征,也就只有一个斜率。因为斜率在所有箱子中是相同的,所以它似乎不是很有用。我们更希望每个箱子都有一个不同的斜率。为了实现这一点,我们可以添加交互特征或乘积特征,用来表示数据点所在的箱子以及数据点在x轴上的位置。这个特征是箱子指示符与原始特征的乘积。下面来创建数据集:
import numpy as np
import mglearn
#import matplotlib.pyplot as plt
#from sklearn.linear_model import LinearRegression
#from sklearn.tree import DecisionTreeRegressor
#from sklearn.preprocessing import OneHotEncoder
from sklearn.preprocessing import KBinsDiscretizerX, y = mglearn.datasets.make_wave(n_samples=100)
line = np.linspace(-3, 3, 1000, endpoint=False).reshape(-1, 1)# 生成10个箱子
#kb = KBinsDiscretizer(n_bins=10, strategy='uniform')
#kb.fit(X)kb = KBinsDiscretizer(n_bins=10, strategy='uniform', encode='onehot-dense')
kb.fit(X)
#X_binned = kb.transform(X)
# 记录每个数据点所属的箱子。
X_binned = kb.transform(X)
line_binned = kb.transform(line)# 加入原始特征
X_combined = np.hstack([X, X_binned])
#print(X_combined.shape)line_combined = np.hstack([line, line_binned])# 创建数据集
X_product = np.hstack([X_binned, X * X_binned])
print(X_product.shape)输出:(100, 20) 。这个数据集现在有20个特征:数据点所在箱子的指示符与原始特征和箱子指示符的乘积。可以将乘积特征看作每个箱子x轴特征的单独副本。它在箱子内等于原始特征,在其他 位置等于零。下面我们代码绘图给出线性模型在这种新表示上的结果:
import numpy as np
import mglearn
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
#from sklearn.tree import DecisionTreeRegressor
#from sklearn.preprocessing import OneHotEncoder
from sklearn.preprocessing import KBinsDiscretizerX, y = mglearn.datasets.make_wave(n_samples=100)
line = np.linspace(-3, 3, 1000, endpoint=False).reshape(-1, 1)# 生成10个箱子
#kb = KBinsDiscretizer(n_bins=10, strategy='uniform')
#kb.fit(X)kb = KBinsDiscretizer(n_bins=10, strategy='uniform', encode='onehot-dense')
kb.fit(X)
#X_binned = kb.transform(X)
# 记录每个数据点所属的箱子。
X_binned = kb.transform(X)
line_binned = kb.transform(line)# 加入原始特征
X_combined = np.hstack([X, X_binned])
#print(X_combined.shape)# 创建数据集
X_product = np.hstack([X_binned, X * X_binned])
#print(X_product.shape)reg = LinearRegression().fit(X_product, y)line_product = np.hstack([line_binned, line * line_binned])plt.plot(line, reg.predict(line_product), label='linear regression product')
plt.vlines(kb.bin_edges_[0], -3, 3, linewidth=1, alpha=.2)
plt.plot(X[:, 0], y, 'o', c='k')
plt.ylabel("Regression output")
plt.xlabel("Input feature")
plt.legend(loc="best")
plt.show()输出图形:

上图显示每个箱子具有不同的偏移和斜率。使用分箱是扩展连续特征的一种方法。另一种方法是 使用原始特征的多项式(polynomial)。对于给定特征x,我们可以考虑x ** 2、x ** 3、x ** 4,等等。这在preprocessing模块的PolynomialFeatures中实现:
import numpy as np
import mglearn
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
#from sklearn.tree import DecisionTreeRegressor
#from sklearn.preprocessing import OneHotEncoder
from sklearn.preprocessing import KBinsDiscretizer
from sklearn.preprocessing import PolynomialFeaturesX, y = mglearn.datasets.make_wave(n_samples=100)
line = np.linspace(-3, 3, 1000, endpoint=False).reshape(-1, 1)# 生成10个箱子
#kb = KBinsDiscretizer(n_bins=10, strategy='uniform')
#kb.fit(X)kb = KBinsDiscretizer(n_bins=10, strategy='uniform', encode='onehot-dense')
kb.fit(X)
#X_binned = kb.transform(X)
# 记录每个数据点所属的箱子。
X_binned = kb.transform(X)
line_binned = kb.transform(line)# 加入原始特征
X_combined = np.hstack([X, X_binned])
#print(X_combined.shape)# 创建数据集
#X_product = np.hstack([X_binned, X * X_binned])
#print(X_product.shape)# 包含直到x ** 10的多项式:
# 默认的"include_bias=True"添加恒等于1的常数特征
poly = PolynomialFeatures(degree=10, include_bias=False)
poly.fit(X)
X_poly = poly.transform(X)
# 多项式的次数为 10,因此生成10个特征:
print("X_poly.shape: {}".format(X_poly.shape))输出:X_poly.shape: (100, 10)
比较X_ploy和X的元素:
import numpy as np
import mglearn
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
#from sklearn.tree import DecisionTreeRegressor
#from sklearn.preprocessing import OneHotEncoder
from sklearn.preprocessing import KBinsDiscretizer
from sklearn.preprocessing import PolynomialFeaturesX, y = mglearn.datasets.make_wave(n_samples=100)
line = np.linspace(-3, 3, 1000, endpoint=False).reshape(-1, 1)# 生成10个箱子
#kb = KBinsDiscretizer(n_bins=10, strategy='uniform')
#kb.fit(X)kb = KBinsDiscretizer(n_bins=10, strategy='uniform', encode='onehot-dense')
kb.fit(X)
#X_binned = kb.transform(X)
# 记录每个数据点所属的箱子。
X_binned = kb.transform(X)
line_binned = kb.transform(line)# 加入原始特征
X_combined = np.hstack([X, X_binned])
#print(X_combined.shape)# 创建数据集
#X_product = np.hstack([X_binned, X * X_binned])
#print(X_product.shape)# 包含直到x ** 10的多项式:
# 默认的"include_bias=True"添加恒等于1的常数特征
poly = PolynomialFeatures(degree=10, include_bias=False)
poly.fit(X)
X_poly = poly.transform(X)
# 多项式的次数为 10,因此生成10个特征:
print("X_poly.shape: {}".format(X_poly.shape))# 比较 X_poly 和 X 的元素:
print("Entries of X:\n{}".format(X[:5]))
print("Entries of X_poly:\n{}".format(X_poly[:5]))输出:
Entries of X:
[[-0.75275929]
[ 2.70428584]
[ 1.39196365]
[ 0.59195091]
[-2.06388816]]
Entries of X_poly:
[[-7.52759287e-01 5.66646544e-01 -4.26548448e-01 3.21088306e-01
-2.41702204e-01 1.81943579e-01 -1.36959719e-01 1.03097700e-01
-7.76077513e-02 5.84199555e-02]
[ 2.70428584e+00 7.31316190e+00 1.97768801e+01 5.34823369e+01
1.44631526e+02 3.91124988e+02 1.05771377e+03 2.86036036e+03
7.73523202e+03 2.09182784e+04]
[ 1.39196365e+00 1.93756281e+00 2.69701700e+00 3.75414962e+00
5.22563982e+00 7.27390068e+00 1.01250053e+01 1.40936394e+01
1.96178338e+01 2.73073115e+01]
[ 5.91950905e-01 3.50405874e-01 2.07423074e-01 1.22784277e-01
7.26822637e-02 4.30243318e-02 2.54682921e-02 1.50759786e-02
8.92423917e-03 5.28271146e-03]
[-2.06388816e+00 4.25963433e+00 -8.79140884e+00 1.81444846e+01
-3.74481869e+01 7.72888694e+01 -1.59515582e+02 3.29222321e+02
-6.79478050e+02 1.40236670e+03]]
我们可以通过调用 get_feature_names_out 方法来获取特征的语义,给出每个特征的指数:
import numpy as np
import mglearn
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
#from sklearn.tree import DecisionTreeRegressor
#from sklearn.preprocessing import OneHotEncoder
from sklearn.preprocessing import KBinsDiscretizer
from sklearn.preprocessing import PolynomialFeaturesX, y = mglearn.datasets.make_wave(n_samples=100)
line = np.linspace(-3, 3, 1000, endpoint=False).reshape(-1, 1)# 生成10个箱子
#kb = KBinsDiscretizer(n_bins=10, strategy='uniform')
#kb.fit(X)kb = KBinsDiscretizer(n_bins=10, strategy='uniform', encode='onehot-dense')
kb.fit(X)
#X_binned = kb.transform(X)
# 记录每个数据点所属的箱子。
X_binned = kb.transform(X)
line_binned = kb.transform(line)# 加入原始特征
X_combined = np.hstack([X, X_binned])
#print(X_combined.shape)# 创建数据集
#X_product = np.hstack([X_binned, X * X_binned])
#print(X_product.shape)# 包含直到x ** 10的多项式:
# 默认的"include_bias=True"添加恒等于1的常数特征
poly = PolynomialFeatures(degree=10, include_bias=False)
poly.fit(X)
X_poly = poly.transform(X)
# 多项式的次数为 10,因此生成10个特征:
print("X_poly.shape: {}".format(X_poly.shape))# 比较 X_poly 和 X 的元素:
print("Entries of X:\n{}".format(X[:5]))
print("Entries of X_poly:\n{}".format(X_poly[:5]))#调用 get_feature_names_out 方法来获取特征的语义,给出每个特征的指数
print("Polynomial feature names:\n{}".format(poly.get_feature_names_out()))输出:
Polynomial feature names:
['x0' 'x0^2' 'x0^3' 'x0^4' 'x0^5' 'x0^6' 'x0^7' 'x0^8' 'x0^9' 'x0^10']
可以看到,X_poly 的第一列与 X 完全对应,而其他列则是第一列的幂。有趣的是,可以发现有些值非常大。第二行有大于 20000 的元素,数量级与其他行都不相同。将多项式特征与线性回归模型一起使用,可以得到经典的多项式回归(polynomial regression)模型,见如下代码实现:
import numpy as np
import mglearn
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
#from sklearn.tree import DecisionTreeRegressor
#from sklearn.preprocessing import OneHotEncoder
from sklearn.preprocessing import KBinsDiscretizer
from sklearn.preprocessing import PolynomialFeaturesX, y = mglearn.datasets.make_wave(n_samples=100)
line = np.linspace(-3, 3, 1000, endpoint=False).reshape(-1, 1)# 生成10个箱子
#kb = KBinsDiscretizer(n_bins=10, strategy='uniform')
#kb.fit(X)kb = KBinsDiscretizer(n_bins=10, strategy='uniform', encode='onehot-dense')
kb.fit(X)
#X_binned = kb.transform(X)
# 记录每个数据点所属的箱子。
X_binned = kb.transform(X)
#line_binned = kb.transform(line)# 加入原始特征
X_combined = np.hstack([X, X_binned])
#print(X_combined.shape)# 创建数据集
#X_product = np.hstack([X_binned, X * X_binned])
#print(X_product.shape)# 包含直到x ** 10的多项式:
# 默认的"include_bias=True"添加恒等于1的常数特征
poly = PolynomialFeatures(degree=10, include_bias=False)
poly.fit(X)
X_poly = poly.transform(X)
# 多项式的次数为 10,因此生成10个特征:
#print("X_poly.shape: {}".format(X_poly.shape))# 比较 X_poly 和 X 的元素:
#print("Entries of X:\n{}".format(X[:5]))
#print("Entries of X_poly:\n{}".format(X_poly[:5]))#调用 get_feature_names 方法来获取特征的语义,给出每个特征的指数
#print("Polynomial feature names:\n{}".format(poly.get_feature_names_out()))reg = LinearRegression().fit(X_poly, y)line_poly = poly.transform(line)
plt.plot(line, reg.predict(line_poly), label='polynomial linear regression')
plt.plot(X[:, 0], y, 'o', c='k')
plt.ylabel("Regression output")
plt.xlabel("Input feature")
plt.legend(loc="best")
plt.show()输出图形:

上图是具有 10 次多项式特征的线性回归。多项式特征在这个一维数据上得到了非常平滑的拟合。但高次多项式在边界上或数据很少的区域可能有极端的表现。作为对比,下面是在原始数据上学到的核SVM模型,没有做任何变换:
import numpy as np
import mglearn
import matplotlib.pyplot as plt
from sklearn.svm import SVRX, y = mglearn.datasets.make_wave(n_samples=100)
line = np.linspace(-3, 3, 1000, endpoint=False).reshape(-1, 1)for gamma in [1, 10]:svr = SVR(gamma=gamma).fit(X, y)plt.plot(line, svr.predict(line), label='SVR gamma={}'.format(gamma))plt.plot(X[:, 0], y, 'o', c='k')
plt.ylabel("Regression output")
plt.xlabel("Input feature")
plt.legend(loc="best")
plt.show()输出图形(对于RBF核的SVM,使用不同 gamma 参数的对比):

使用更加复杂的模型(即核 SVM),能够学到一个与多项式回归的复杂度类似的预测结果,且不需要进行显式的特征变换。
相关文章:

Python机器学习笔记(十八、交互特征与多项式特征)
添加原始数据的交互特征(interaction feature)和多项式特征(polynomial feature)可以丰富特征表示,特别是对于线性模型。这种特征工程可以用统计建模和许多实际的机器学习应用中。 上一次学习:线性模型对w…...

《跟我学Spring Boot开发》系列文章索引❤(2025.01.09更新)
章节文章名备注第1节Spring Boot(1)基于Eclipse搭建Spring Boot开发环境环境搭建第2节Spring Boot(2)解决Maven下载依赖缓慢的问题给火车头提提速第3节Spring Boot(3)教你手工搭建Spring Boot项目纯手工玩法…...

【AI进化论】 如何让AI帮我们写一个项目系列:将Mysql生成md文档
一、python脚本 下面给出一个简易 Python 脚本示例,演示如何自动获取所有表的结构,并生成一份 Markdown 文件。你可根据自己的需求做修改或使用其他编程语言。 import mysql.connector# ------------------------ # 1. 连接数据库 # -----------------…...

(已开源-AAAI25) RCTrans:雷达相机融合3D目标检测模型
在雷达相机融合三维目标检测中,雷达点云稀疏、噪声较大,在相机雷达融合过程中提出了很多挑战。为了解决这个问题,我们引入了一种新的基于query的检测方法 Radar-Camera Transformer (RCTrans)。具体来说: 首先设计了一个雷达稠密…...

Elasticsearch:在 HNSW 中提前终止以实现更快的近似 KNN 搜索
作者:来自 Elastic Tommaso Teofili 了解如何使用智能提前终止策略让 HNSW 加快 KNN 搜索速度。 在高维空间中高效地找到最近邻的挑战是向量搜索中最重要的挑战之一,特别是当数据集规模增长时。正如我们之前的博客文章中所讨论的,当数据集规模…...

unittest VS pytest
以下是 unittest 和 pytest 框架的对比表格: 特性unittestpytest设计理念基于类的设计,类似于 Java 的 JUnit更简洁,基于函数式编程设计,支持类和函数两种方式测试编写需要继承 unittest.TestCase 类,方法以 test_ 开…...
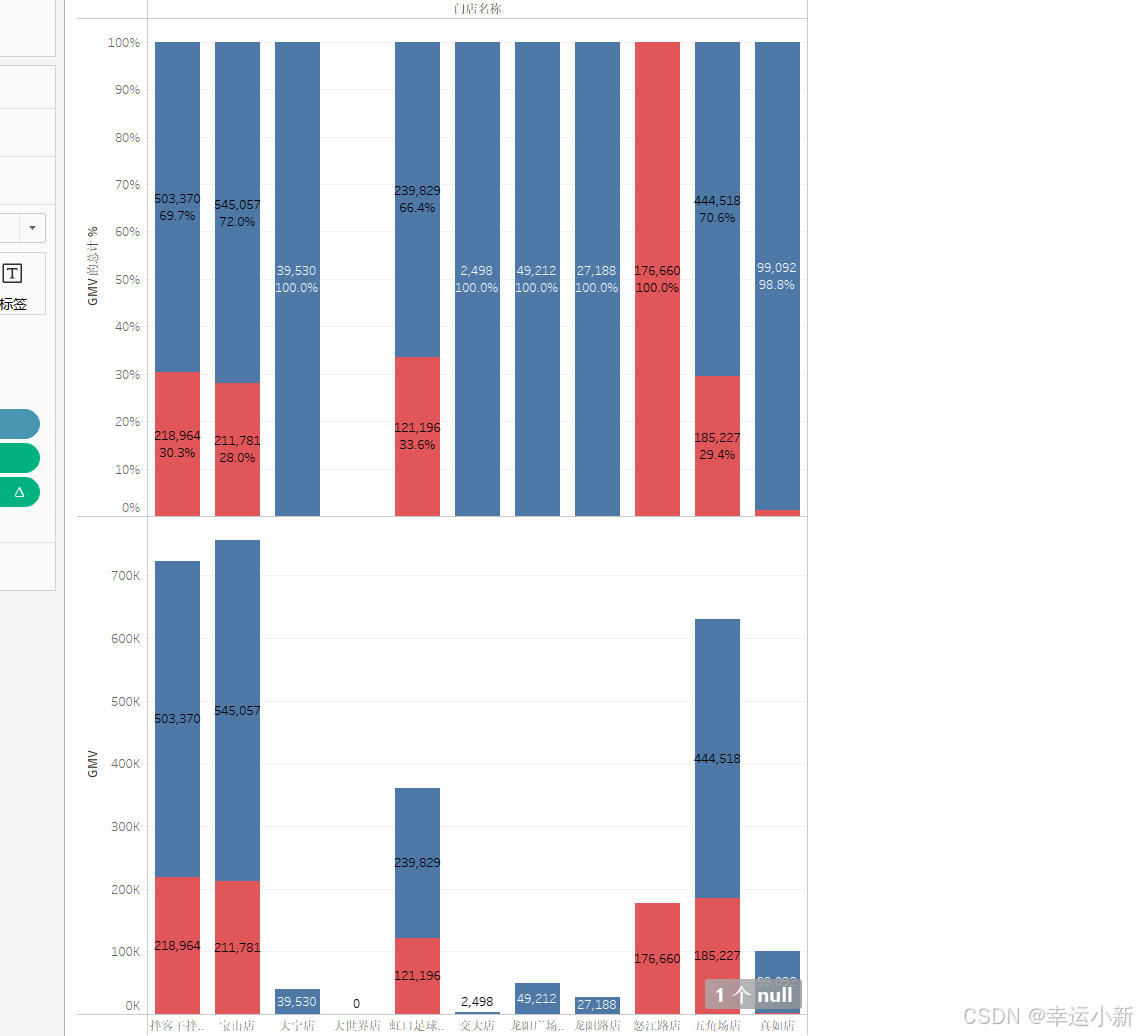
Tableau数据可视化与仪表盘搭建-基础图表制作
目录 对比分析:比大小 柱状图 条形图 数据钻取 筛选器 热力图 气泡图 变化分析:看趋势 折线图 预测 面积图 关系分布:看位置 散点图 直方图 地图 构成分析:看占比 饼图 树地图 堆积图 对比分析:比大…...

Center Loss 和 ArcFace Loss 笔记
一、Center Loss 1. 定义 Center Loss 旨在最小化类内特征的离散程度,通过约束样本特征与其类别中心之间的距离,提高类内特征的聚合性。 2. 公式 对于样本 xi 和其类别yi,Center Loss 的公式为: xi: 当前样本的特征向量&…...

3125: 【入门】求1/1+1/2+2/3+3/5+5/8+8/13+13/21……的前n项的和
文章目录 题目描述输入输出样例输入样例输出 题目描述 求1/11/22/33/55/88/1313/2121/34……的前n项的和。 输入 第1行:一个整数n(1 < n < 30 )。 输出 一行:一个小数,即前n项之和(保留3位小数&…...

如何确保获取的淘宝详情页数据的准确性和时效性?
要确保获取的淘宝详情页数据的准确性和时效性,可从以下几个方面着手: 合法合规获取数据 遵守平台规则:在获取淘宝详情页数据之前,务必仔细阅读并严格遵守淘宝平台的使用协议和相关规定。明确哪些数据可以获取、以何种方式获取以及…...

云计算是如何帮助企业实现高可用性的
想象一下,你正在享受一个悠闲的周末,突然接到同事的电话:公司的核心系统宕机了!这个场景对很多IT从业者来说并不陌生。但在云计算时代,这样的噩梦正在逐渐远去。 一位前辈告诉我:"在技术世界里&#…...

143.《python中使用pymongo》
文章目录 pymongo安装pymongo连接数据库mongodb操作创建数据库判断数据库是否存在创建集合判断集合是否已经存在插入集合插入一条多条插入 查询数据查询一条数据查询所有数据查询指定字段的数据统计查询统计所有记录数按条件统计记录数分页列表查询比较查询$eq$gt$gte$in$lt$lt…...

Babylon.js 的 Mesh 与 Unity 的 GameObject:深入对比与分析
在 3D 开发领域,Babylon.js 和 Unity 是两款极具影响力的引擎,分别在 Web 平台和游戏开发领域占据重要地位。要深入理解这两款引擎的异同,从其核心对象——Babylon.js 的 Mesh 和 Unity 的 GameObject ——入手进行对比,是…...
MySQL安装,配置教程
一、Linux在线yum仓库安装 打开MySQL官方首页,链接为:https://www.mysql.com/ 界面如下: 在该页面中找到【DOWNOADS】选项卡,点击进入下载页面。 在下载界面中,可以看到不同版本的下载链接,这里选择【My…...
)
Android折叠屏适配(权宜之计)
现在折叠屏手机出了也有一段时间了,但是除了大厂app,其他app适配折叠屏还是比较少,如果真的想做好折叠屏完全适配,那这个文章可能并不适合,这里只是一个简单适配的思路。 如果原先你的app已经适配了平板,那…...

Spark是什么?Flink和Spark区别
Spark是什么?Flink和Spark区别 一、Spark二、Spark和Flink区别三、总结 一、Spark Apache Spark 是一个开源的大数据处理框架,主要用于大规模数据处理和分析。它支持多种数据处理模式,包括批处理、流处理、SQL 查询、机器学习和图处理等。 核…...

Cocos Creator 3.8 修改纹理像素值
修改的代码: import { _decorator, Component, RenderTexture, Sprite, Texture2D, ImageAsset, SpriteFrame, Vec2, gfx, director, log, math, v2 } from cc;const { ccclass, property } _decorator;ccclass(GradientTransparency) export class GradientTrans…...

如何评价deepseek-V3 VS OpenAI o1 自然语言处理成Sql的能力
DeepSeek-V3 介绍 在目前大模型主流榜单中,DeepSeek-V3 在开源模型中位列榜首,与世界上最先进的闭源模型不分伯仲。 准备工作: 笔者只演示实例o1 VS DeepSeek-V3两个模型,大家可以自行验证结果或者实验更多场景,同时…...

SQL左连接的两种不同情况示例和外连接示例
Oracle;有2个表如下; 执行下图选中的左连接; 左表10条记录,右表3条记录,结果是10条记录; 执行下图的左连接, 老师表为左表,学生表为右表,结果会显示每个老师,…...

【渗透测试术语总结】
Top 渗透测试常用专业术语 相信大家和我一样,搞不清这些专业名词的区别,所以我来整理一下。 1. POC、EXP、Payload与Shellcode POC:全称 Proof of Concept ,中文 概念验证 ,常指一段漏洞证明的代码。 EXP…...

linux之kylin系统nginx的安装
一、nginx的作用 1.可做高性能的web服务器 直接处理静态资源(HTML/CSS/图片等),响应速度远超传统服务器类似apache支持高并发连接 2.反向代理服务器 隐藏后端服务器IP地址,提高安全性 3.负载均衡服务器 支持多种策略分发流量…...

PHP和Node.js哪个更爽?
先说结论,rust完胜。 php:laravel,swoole,webman,最开始在苏宁的时候写了几年php,当时觉得php真的是世界上最好的语言,因为当初活在舒适圈里,不愿意跳出来,就好比当初活在…...

大语言模型如何处理长文本?常用文本分割技术详解
为什么需要文本分割? 引言:为什么需要文本分割?一、基础文本分割方法1. 按段落分割(Paragraph Splitting)2. 按句子分割(Sentence Splitting)二、高级文本分割策略3. 重叠分割(Sliding Window)4. 递归分割(Recursive Splitting)三、生产级工具推荐5. 使用LangChain的…...

macOS多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用
文章目录 问题现象问题原因解决办法 问题现象 macOS启动台(Launchpad)多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用。 问题原因 很明显,都是Google家的办公全家桶。这些应用并不是通过独立安装的…...

Unit 1 深度强化学习简介
Deep RL Course ——Unit 1 Introduction 从理论和实践层面深入学习深度强化学习。学会使用知名的深度强化学习库,例如 Stable Baselines3、RL Baselines3 Zoo、Sample Factory 和 CleanRL。在独特的环境中训练智能体,比如 SnowballFight、Huggy the Do…...

Spring数据访问模块设计
前面我们已经完成了IoC和web模块的设计,聪明的码友立马就知道了,该到数据访问模块了,要不就这俩玩个6啊,查库势在必行,至此,它来了。 一、核心设计理念 1、痛点在哪 应用离不开数据(数据库、No…...
)
.Net Framework 4/C# 关键字(非常用,持续更新...)
一、is 关键字 is 关键字用于检查对象是否于给定类型兼容,如果兼容将返回 true,如果不兼容则返回 false,在进行类型转换前,可以先使用 is 关键字判断对象是否与指定类型兼容,如果兼容才进行转换,这样的转换是安全的。 例如有:首先创建一个字符串对象,然后将字符串对象隐…...

React---day11
14.4 react-redux第三方库 提供connect、thunk之类的函数 以获取一个banner数据为例子 store: 我们在使用异步的时候理应是要使用中间件的,但是configureStore 已经自动集成了 redux-thunk,注意action里面要返回函数 import { configureS…...

JavaScript 数据类型详解
JavaScript 数据类型详解 JavaScript 数据类型分为 原始类型(Primitive) 和 对象类型(Object) 两大类,共 8 种(ES11): 一、原始类型(7种) 1. undefined 定…...

Redis:现代应用开发的高效内存数据存储利器
一、Redis的起源与发展 Redis最初由意大利程序员Salvatore Sanfilippo在2009年开发,其初衷是为了满足他自己的一个项目需求,即需要一个高性能的键值存储系统来解决传统数据库在高并发场景下的性能瓶颈。随着项目的开源,Redis凭借其简单易用、…...
