数据结构与算法之二叉树: LeetCode 654. 最大二叉树 (Ts版)
最大二叉树
- https://leetcode.cn/problems/maximum-binary-tree/
描述
- 给定一个不重复的整数数组 nums 。 最大二叉树 可以用下面的算法从 nums 递归地构建:
- 创建一个根节点,其值为 nums 中的最大值
- 递归地在最大值 左边 的 子数组前缀上 构建左子树
- 递归地在最大值 右边 的 子数组后缀上 构建右子树
- 返回 nums 构建的 最大二叉树
示例 1

输入:nums = [3,2,1,6,0,5]
输出:[6,3,5,null,2,0,null,null,1]
解释:递归调用如下所示:
- [3,2,1,6,0,5] 中的最大值是 6 ,左边部分是 [3,2,1] ,右边部分是 [0,5] 。
- [3,2,1] 中的最大值是 3 ,左边部分是 [] ,右边部分是 [2,1] 。
- 空数组,无子节点。
- [2,1] 中的最大值是 2 ,左边部分是 [] ,右边部分是 [1] 。
- 空数组,无子节点。
- 只有一个元素,所以子节点是一个值为 1 的节点。
- [0,5] 中的最大值是 5 ,左边部分是 [0] ,右边部分是 [] 。
- 只有一个元素,所以子节点是一个值为 0 的节点。
- 空数组,无子节点。
- [3,2,1] 中的最大值是 3 ,左边部分是 [] ,右边部分是 [2,1] 。
示例 2

输入:nums = [3,2,1]
输出:[3,null,2,null,1]
提示
- 1 <= nums.length <= 1000
- 0 <= nums[i] <= 1000
- nums 中的所有整数 互不相同
Typescript 版算法实现
1 ) 方案1:递归
/*** Definition for a binary tree node.* class TreeNode {* val: number* left: TreeNode | null* right: TreeNode | null* constructor(val?: number, left?: TreeNode | null, right?: TreeNode | null) {* this.val = (val===undefined ? 0 : val)* this.left = (left===undefined ? null : left)* this.right = (right===undefined ? null : right)* }* }*/function constructMaximumBinaryTree(nums: number[]): TreeNode | null {const construct = (nums, left, right) => {if (left > right) return null;let best = left;for (let i = left + 1; i <= right; ++i) {if (nums[i] > nums[best]) {best = i;}}const node = new TreeNode(nums[best]);node.left = construct(nums, left, best - 1);node.right = construct(nums, best + 1, right);return node;}return construct(nums, 0, nums.length - 1);
};2 ) 方案2:单调栈
/*** Definition for a binary tree node.* class TreeNode {* val: number* left: TreeNode | null* right: TreeNode | null* constructor(val?: number, left?: TreeNode | null, right?: TreeNode | null) {* this.val = (val===undefined ? 0 : val)* this.left = (left===undefined ? null : left)* this.right = (right===undefined ? null : right)* }* }*/function constructMaximumBinaryTree(nums: number[]): TreeNode | null {const n = nums.length;const stack = [];const left = new Array(n).fill(-1);const right = new Array(n).fill(-1);const tree = new Array(n).fill(-1);for (let i = 0; i < n; ++i) {tree[i] = new TreeNode(nums[i]);while (stack.length && nums[i] > nums[stack[stack.length - 1]]) {right[stack.pop()] = i;}if (stack.length) {left[i] = stack[stack.length - 1];}stack.push(i);}let root = null;for (let i = 0; i < n; ++i) {if (left[i] === -1 && right[i] === -1) {root = tree[i];} else if (right[i] === -1 || (left[i] !== -1 && nums[left[i]] < nums[right[i]])) {tree[left[i]].right = tree[i];} else {tree[right[i]].left = tree[i];}}return root;
};
3 ) 方案3:单调栈优化
/*** Definition for a binary tree node.* class TreeNode {* val: number* left: TreeNode | null* right: TreeNode | null* constructor(val?: number, left?: TreeNode | null, right?: TreeNode | null) {* this.val = (val===undefined ? 0 : val)* this.left = (left===undefined ? null : left)* this.right = (right===undefined ? null : right)* }* }*/function constructMaximumBinaryTree(nums: number[]): TreeNode | null {const n = nums.length;const stack = [];const tree = new Array(n).fill(0);for (let i = 0; i < n; ++i) {tree[i] = new TreeNode(nums[i]);while (stack.length && nums[i] > nums[stack[stack.length - 1]]) {tree[i].left = tree[stack[stack.length - 1]];stack.pop();}if (stack.length) {tree[stack[stack.length - 1]].right = tree[i];}stack.push(i);}return tree[stack[0]];
};
相关文章:

数据结构与算法之二叉树: LeetCode 654. 最大二叉树 (Ts版)
最大二叉树 https://leetcode.cn/problems/maximum-binary-tree/ 描述 给定一个不重复的整数数组 nums 。 最大二叉树 可以用下面的算法从 nums 递归地构建: 创建一个根节点,其值为 nums 中的最大值递归地在最大值 左边 的 子数组前缀上 构建左子树递归地在最大值…...

Linux 容器漏洞
定义:Linux 容器漏洞是指在容器技术(如 Docker、LXC 等)运行环境中存在的安全弱点。这些漏洞可能存在于容器镜像本身、容器运行时(如 runc)、容器编排工具(如 Kubernetes)或者容器与主机之间的交…...
)
file与io流(1)
-1- java.io.File类的使用 (1) 概述 File类及本章下的各种流,都定义在java.io包下。一个File对象代表硬盘或网络中可能存在的一个文件或者文件目录(俗称文件夹),与平台无关。(体会万事万物皆…...

忘记了PDF文件的密码,怎么办?
PDF文件可以加密,大家都不陌生,并且大家应该也都知道PDF文件有两种密码,一个打开密码、一个限制编辑密码,因为PDF文件设置了密码,那么打开、编辑PDF文件就会受到限制。忘记了PDF密码该如何解密? PDF和offi…...

Linux权限管理(用户和权限之间的关系)
Linux系列 文章目录 Linux系列一、Linux下用户类型二、普通权限的基本概念2.1、Linux中权限的类别2.2、Linux中权限对应的三种身份2.3、文件权限的标识 三、文件权限设置四、修改文件属主和属组4.1、chown修改文件的属主4.2、修改所属组 五、文件掩码六、目录权限 一、Linux下用…...
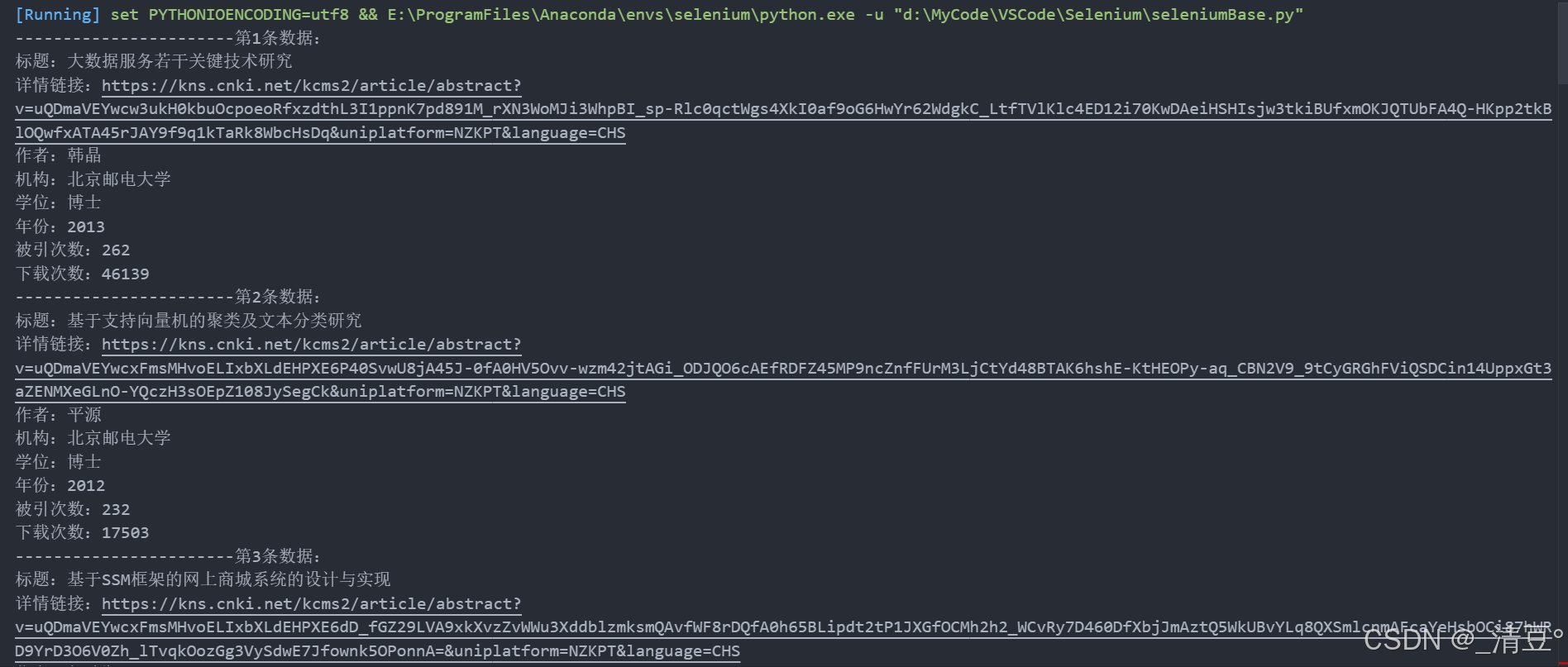
Python Selenium库入门使用,图文详细。附网页爬虫、web自动化操作等实战操作。
文章目录 前言1 创建conda环境安装Selenium库2 浏览器驱动下载(以Chrome和Edge为例)3 基础使用(以Chrome为例演示)3.1 与浏览器相关的操作3.1.1 打开/关闭浏览器3.1.2 访问指定域名的网页3.1.3 控制浏览器的窗口大小3.1.4 前进/后…...
【Uniapp-Vue3】使用defineExpose暴露子组件的属性及方法
如果我们想要让父组件访问到子组件中的变量和方法,就需要使用defineExpose暴露: defineExpose({ 变量 }) 子组件配置 父组件配置 父组件要通过onMounted获取到子组件的DOM 传递多个属性和方法 子组件 父组件...
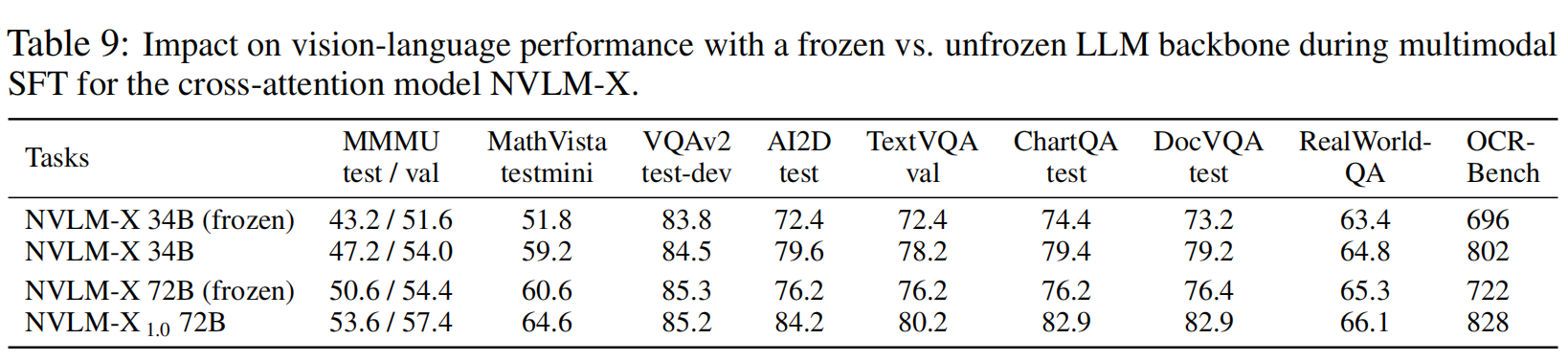
【多模态LLM】英伟达NVLM多模态大模型训练细节和数据集
前期笔者介绍了OCR-free的多模态大模型,可以参考:【多模态&文档智能】OCR-free感知多模态大模型技术链路及训练数据细节,其更偏向于训练模型对于密集文本的感知能力。本文看一看英伟达出品的多模态大模型NVLM-1.0系列,虽然暂未…...

HTTP详解——HTTP基础
HTTP 基本概念 HTTP 是超文本传输协议 (HyperText Transfer Protocol) 超文本传输协议(HyperText Transfer Protocol) HTTP 是一个在计算机世界里专门在 两点 之间 传输 文字、图片、音视频等 超文本 数据的 约定和规范 1. 协议 约定和规范 2. 传输 两点之间传输…...

MySQL教程之:输入查询
如上一节所述,确保您已连接到服务器。这样做本身不会选择任何要使用的数据库,但没关系。在这一点上,了解一下如何发出查询比直接创建表、加载数据和从中检索数据更重要。本节介绍输入查询的基本原则,使用几个查询,您可…...
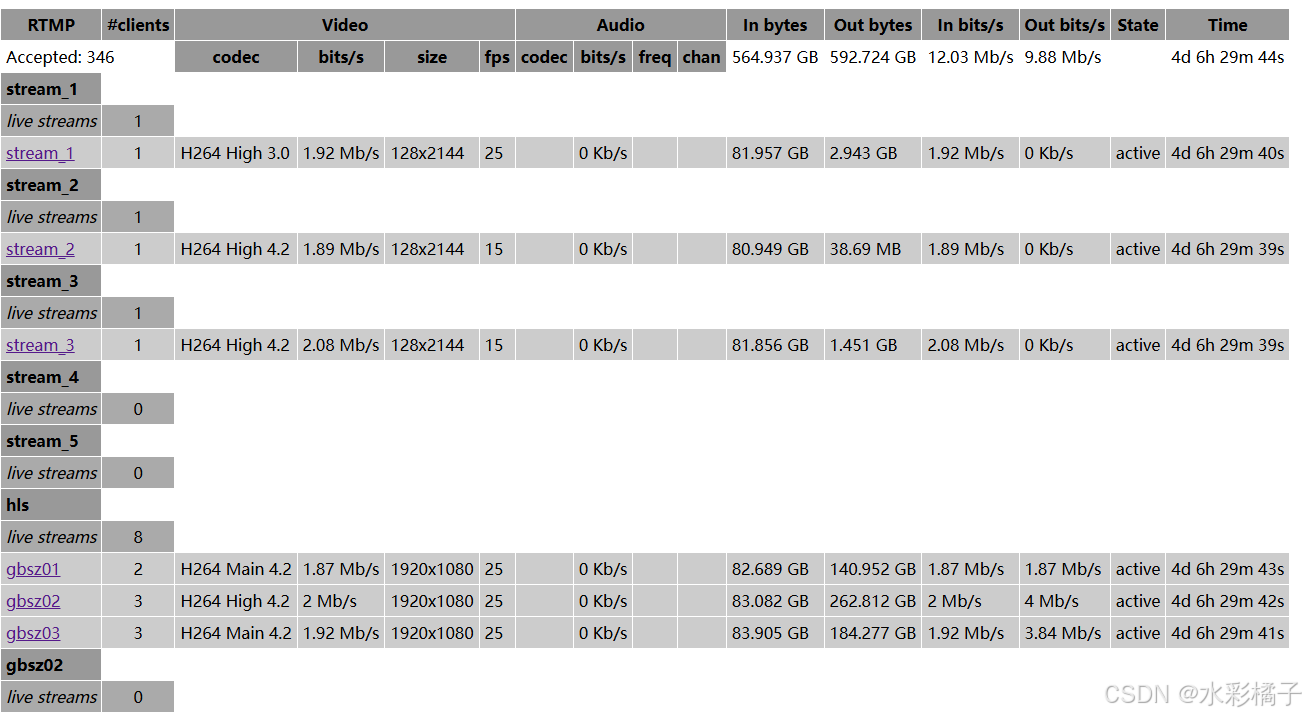
docker+ffmpeg+nginx+rtmp 拉取摄像机视频
1、构造程序容器镜像 app.py import subprocess import json import time import multiprocessing import socketdef check_rtmp_server(host, port, timeout5):try:with socket.create_connection((host, port), timeout):print(f"RTMP server at {host}:{port} is avai…...
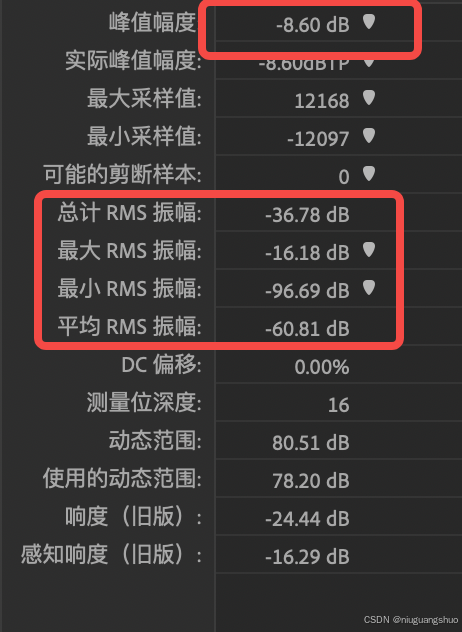
不同音频振幅dBFS计算方法
1. 振幅的基本概念 振幅是描述音频信号强度的一个重要参数。它通常表示为信号的幅度值,幅度越大,声音听起来就越响。为了更好地理解和处理音频信号,通常会将振幅转换为分贝(dB)单位。分贝是一个对数单位,能…...
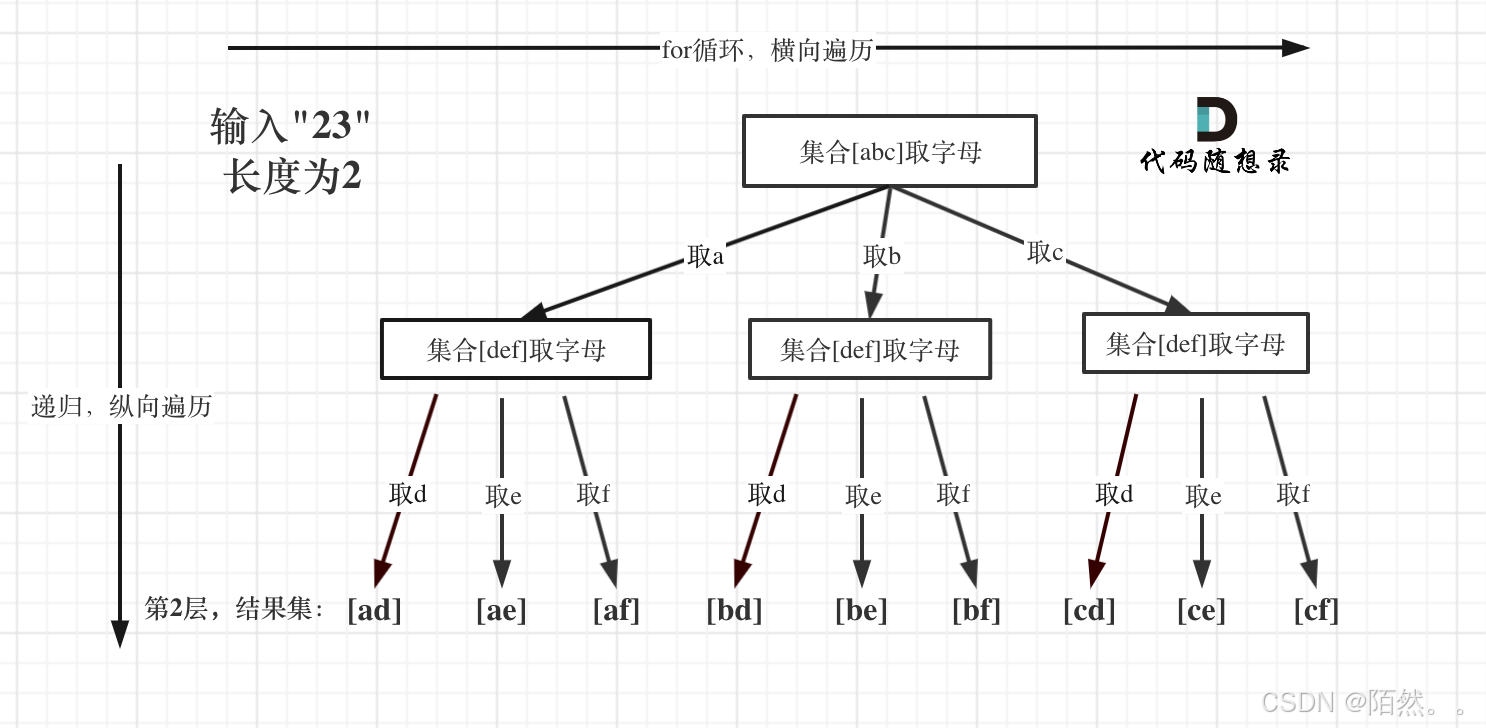
【17. 电话号码的字母组合 中等】
题目: 给定一个仅包含数字 2-9 的字符串,返回所有它能表示的字母组合。答案可以按 任意顺序 返回。 给出数字到字母的映射如下(与电话按键相同)。注意 1 不对应任何字母。 示例 1: 输入:digits “23”…...
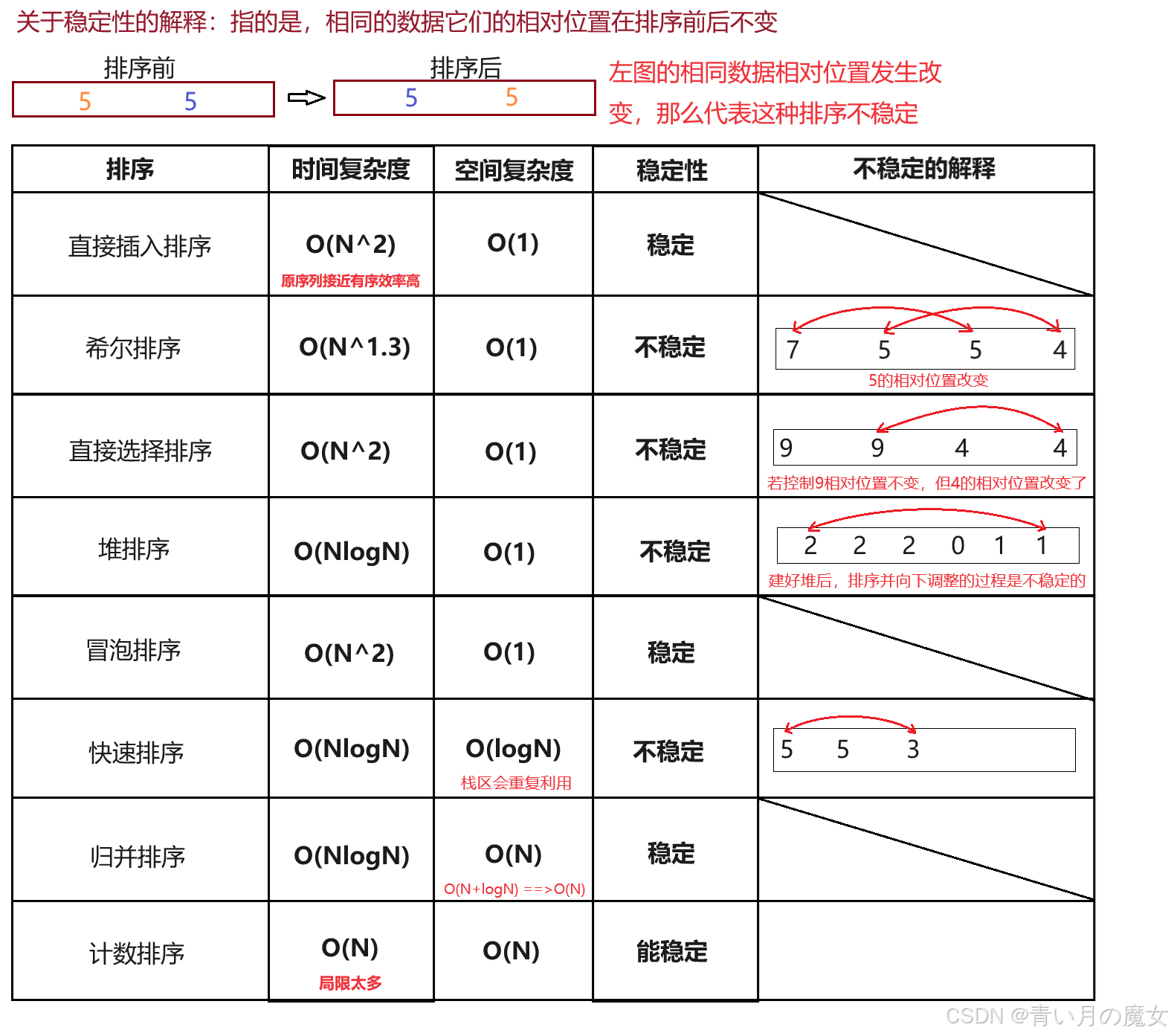
数据结构初阶---排序
一、排序相关概念与运用 1.排序相关概念 排序:所谓排序,就是使一串记录,按照其中的某个或某些关键字的大小,递增或递减的排列起来的操作。 稳定性:假定在待排序的记录序列中,存在多个具有相同的关键字的…...
【从0-1实现一个前端脚手架】
目录 介绍为什么需要脚手架?一个脚手架应该具备哪些功能? 脚手架实现初始化项目相关依赖实现脚手架 发布 介绍 为什么需要脚手架? 脚手架本质就是一个工具,作用是能够让使用者专注于写代码,它可以让我们只用一个命令…...
AI文章管理系统(自动生成图文分发到分站)
最近帮一个网上的朋友做了一套AI文章生成系统。他的需求是这样: 1、做一个服务端转接百度文心一言的生成文章的API接口。 2、服务端能注册用户,用户在服务端注册充值后可以获取一个令牌,这个令牌填写到客户端,客户端就可以根据客…...

【Leetcode 每日一题】3270. 求出数字答案
问题背景 给你三个 正 整数 n u m 1 num_1 num1, n u m 2 num_2 num2 和 n u m 3 num_3 num3。 数字 n u m 1 num_1 num1, n u m 2 num_2 num2 和 n u m 3 num_3 num3 的数字答案 k e y key key 是一个四位数,定义如下&…...
基于单片机的无线气象仪系统设计(论文+源码)
1系统方案设计 如图2.1所示为无线气象仪系统设计框架。系统设计采用STM32单片机作为主控制器,结合DHT11温湿度传感器、光敏传感器、BMP180气压传感器、PR-3000-FS-N01风速传感器实现气象环境的温度、湿度、光照、气压、风速等环境数据的检测,并通过OLED1…...

【数据库】Mysql精简回顾复习
一、概念 数据库(DB):数据存储的仓库数据库管理系统(DBMS):操纵和管理数据库的大型软件SQL:操作关系型数据库的编程语言,是一套标准关系型数据库(RDBMS)&…...

深入理解 HTTP 的 GET、POST 方法与 Request 和 Response
HTTP 协议是构建 Web 应用的基石,GET 和 POST 是其中最常用的请求方法。无论是前端开发、后端开发,还是接口测试,对它们的深入理解都显得尤为重要。在本文中,我们将介绍 GET 和 POST 方法,以及 Request 和 Response 的…...

Python爬虫实战:研究feedparser库相关技术
1. 引言 1.1 研究背景与意义 在当今信息爆炸的时代,互联网上存在着海量的信息资源。RSS(Really Simple Syndication)作为一种标准化的信息聚合技术,被广泛用于网站内容的发布和订阅。通过 RSS,用户可以方便地获取网站更新的内容,而无需频繁访问各个网站。 然而,互联网…...

对WWDC 2025 Keynote 内容的预测
借助我们以往对苹果公司发展路径的深入研究经验,以及大语言模型的分析能力,我们系统梳理了多年来苹果 WWDC 主题演讲的规律。在 WWDC 2025 即将揭幕之际,我们让 ChatGPT 对今年的 Keynote 内容进行了一个初步预测,聊作存档。等到明…...

React19源码系列之 事件插件系统
事件类别 事件类型 定义 文档 Event Event 接口表示在 EventTarget 上出现的事件。 Event - Web API | MDN UIEvent UIEvent 接口表示简单的用户界面事件。 UIEvent - Web API | MDN KeyboardEvent KeyboardEvent 对象描述了用户与键盘的交互。 KeyboardEvent - Web…...

04-初识css
一、css样式引入 1.1.内部样式 <div style"width: 100px;"></div>1.2.外部样式 1.2.1.外部样式1 <style>.aa {width: 100px;} </style> <div class"aa"></div>1.2.2.外部样式2 <!-- rel内表面引入的是style样…...

【JavaSE】绘图与事件入门学习笔记
-Java绘图坐标体系 坐标体系-介绍 坐标原点位于左上角,以像素为单位。 在Java坐标系中,第一个是x坐标,表示当前位置为水平方向,距离坐标原点x个像素;第二个是y坐标,表示当前位置为垂直方向,距离坐标原点y个像素。 坐标体系-像素 …...

【碎碎念】宝可梦 Mesh GO : 基于MESH网络的口袋妖怪 宝可梦GO游戏自组网系统
目录 游戏说明《宝可梦 Mesh GO》 —— 局域宝可梦探索Pokmon GO 类游戏核心理念应用场景Mesh 特性 宝可梦玩法融合设计游戏构想要素1. 地图探索(基于物理空间 广播范围)2. 野生宝可梦生成与广播3. 对战系统4. 道具与通信5. 延伸玩法 安全性设计 技术选…...

Java多线程实现之Thread类深度解析
Java多线程实现之Thread类深度解析 一、多线程基础概念1.1 什么是线程1.2 多线程的优势1.3 Java多线程模型 二、Thread类的基本结构与构造函数2.1 Thread类的继承关系2.2 构造函数 三、创建和启动线程3.1 继承Thread类创建线程3.2 实现Runnable接口创建线程 四、Thread类的核心…...

AI书签管理工具开发全记录(十九):嵌入资源处理
1.前言 📝 在上一篇文章中,我们完成了书签的导入导出功能。本篇文章我们研究如何处理嵌入资源,方便后续将资源打包到一个可执行文件中。 2.embed介绍 🎯 Go 1.16 引入了革命性的 embed 包,彻底改变了静态资源管理的…...

HDFS分布式存储 zookeeper
hadoop介绍 狭义上hadoop是指apache的一款开源软件 用java语言实现开源框架,允许使用简单的变成模型跨计算机对大型集群进行分布式处理(1.海量的数据存储 2.海量数据的计算)Hadoop核心组件 hdfs(分布式文件存储系统)&a…...

OD 算法题 B卷【正整数到Excel编号之间的转换】
文章目录 正整数到Excel编号之间的转换 正整数到Excel编号之间的转换 excel的列编号是这样的:a b c … z aa ab ac… az ba bb bc…yz za zb zc …zz aaa aab aac…; 分别代表以下的编号1 2 3 … 26 27 28 29… 52 53 54 55… 676 677 678 679 … 702 703 704 705;…...
