【初识扫盲】逆概率加权
我们正在处理一个存在缺失数据的回归模型,并且希望采用一种非参数的逆概率加权方法来调整估计,以应对这种缺失数据的情况。
首先,我们需要明确问题的背景。我们有样本 { ( Y i , X i , r i ) : i = 1 , … , n } \left\{\left(Y_i, \boldsymbol{X}_i, r_i\right): i=1, \ldots, n\right\} {(Yi,Xi,ri):i=1,…,n},其中 Y i Y_i Yi 是因变量, X i \boldsymbol{X}_i Xi 是自变量,而 r i r_i ri 是一个指示变量:如果 Y i Y_i Yi 被观测到,则 r i = 1 r_i = 1 ri=1,否则 r i = 0 r_i = 0 ri=0。缺失机制是随机的,即 r i r_i ri 以概率 π i = π ( X i ) \pi_i = \pi(\boldsymbol{X}_i) πi=π(Xi) 服从伯努利分布,且与 X i \boldsymbol{X}_i Xi 独立。
关键在于,如果我们只使用完全数据(即 r i = 1 r_i = 1 ri=1 的数据),估计结果可能会有偏差,因为缺失数据并不是完全随机的。为了纠正这一点,我们采用逆概率加权法,通过加权来平衡观测数据,以反映整个数据集的情况。
目标函数被修改为:
β ^ h = arg min β ∈ R p ∑ i = 1 n r i π ( X i ) M \hat{\boldsymbol{\beta}}_h = \arg \min_{\boldsymbol{\beta} \in \mathbb{R}^p} \sum_{i=1}^n \frac{r_i}{\pi\left(\boldsymbol{X}_i\right)} M β^h=argβ∈Rpmini=1∑nπ(Xi)riM
让我们逐步解析这个目标函数。
-
逆概率加权:项 r i π i \frac{r_i}{\pi_i} πiri 是逆概率加权的关键。它通过除以观测概率 π i \pi_i πi 来加权每个观测数据点。这样做的目的是,那些更有可能被观测到的数据点会被赋予更高的权重,从而在估计过程中得到更多的关注。这有助于纠正由于缺失数据引入的偏差。
-
函数 M M M:一个目标函数
-
目标函数:整个目标函数是在所有样本上最小化加权和。即使某些 Y i Y_i Yi 缺失,我们也会对所有样本进行求和,但只有当 r i = 1 r_i = 1 ri=1 时,即 Y i Y_i Yi 被观测到时,才会对求和有贡献。
-
期望条件:提到的期望条件 E { r i π i − 1 ∣ X i } = 0 E\left\{\left.\frac{r_i}{\pi_i} - 1 \right| \boldsymbol{X}_i\right\} = 0 E{πiri−1 Xi}=0 表明,逆概率加权调整在给定 X i \boldsymbol{X}_i Xi 的情况下,平均而言是无偏的。这是因为:
E { r i π i ∣ X i } = E ( r i ∣ X i ) π i = π i π i = 1 E\left\{\frac{r_i}{\pi_i} \mid \boldsymbol{X}_i\right\} = \frac{E(r_i \mid \boldsymbol{X}_i)}{\pi_i} = \frac{\pi_i}{\pi_i} = 1 E{πiri∣Xi}=πiE(ri∣Xi)=πiπi=1
因此, E { r i π i − 1 ∣ X i } = 0 E\left\{\frac{r_i}{\pi_i} - 1 \mid \boldsymbol{X}_i\right\} = 0 E{πiri−1∣Xi}=0,这意味着加权项在给定 X i \boldsymbol{X}_i Xi 的情况下,平均而言是中性的,从而有助于无偏估计。
这描述了如何通过逆概率加权法调整回归的目标函数,以处理缺失数据。通过为每个观测数据点分配一个与其观测概率成反比的权重,我们确保估计结果不会因数据缺失机制而产生偏差。
这种方法特别有用,因为它允许我们在不完全排除缺失数据的情况下,有效地利用所有可用数据,从而提高估计的效率和可靠性。
该目标函数通过逆概率加权法调整回归,以处理缺失数据,确保估计结果无偏且高效。 \boxed{ \text{该目标函数通过逆概率加权法调整回归,以处理缺失数据,确保估计结果无偏且高效。} } 该目标函数通过逆概率加权法调整回归,以处理缺失数据,确保估计结果无偏且高效。
这里提到的随机缺失是什么意思?详细解释一下这里的逆概率加权是什么意思,为什么期望是那样的?
我们来详细理解一下“随机缺失”和“逆概率加权”这两个概念,以及为什么在给定 X i \boldsymbol{X}_i Xi的情况下,期望 E { r i π i − 1 ∣ X i } = 0 E\left\{\left.\frac{r_i}{\pi_i} - 1 \right| \boldsymbol{X}_i\right\} = 0 E{πiri−1 Xi}=0。
首先,随机缺失(Missing at Random, MAR) 是指数据的缺失机制与未观测到的数据无关,但可能与已观测到的数据相关。换句话说,给定已观测到的变量 X i \boldsymbol{X}_i Xi,数据是否缺失仅取决于 X i \boldsymbol{X}_i Xi,而不取决于未观测到的 Y i Y_i Yi。这一假设非常重要,因为它允许我们使用已观测到的信息来调整缺失数据的影响,从而减少估计偏差。
接下来,逆概率加权(Inverse Probability Weighting, IPW) 是一种处理缺失数据的方法,通过为每个观测到的数据点分配一个权重,这个权重是其被观测到的概率的倒数。具体来说,如果一个数据点被观测到的概率是 π i \pi_i πi,那么它的权重就是 1 π i \frac{1}{\pi_i} πi1。这样做的目的是使每个数据点在分析中的权重与其被观测到的概率成反比,从而平衡观测数据,使其更具代表性。
现在,我们来探讨为什么在给定 X i \boldsymbol{X}_i Xi的情况下,期望 E { r i π i − 1 ∣ X i } = 0 E\left\{\left.\frac{r_i}{\pi_i} - 1 \right| \boldsymbol{X}_i\right\} = 0 E{πiri−1 Xi}=0。我们逐步分析如下:
E { r i π i − 1 ∣ X i } = E { r i π i ∣ X i } − E { 1 ∣ X i } E\left\{\left.\frac{r_i}{\pi_i} - 1 \right| \boldsymbol{X}_i\right\} = E\left\{\left.\frac{r_i}{\pi_i} \right| \boldsymbol{X}_i\right\} - E\left\{1 \mid \boldsymbol{X}_i\right\} E{πiri−1 Xi}=E{πiri Xi}−E{1∣Xi}
由于 E { 1 ∣ X i } = 1 E\left\{1 \mid \boldsymbol{X}_i\right\} = 1 E{1∣Xi}=1,我们只需计算 E { r i π i ∣ X i } E\left\{\left.\frac{r_i}{\pi_i} \right| \boldsymbol{X}_i\right\} E{πiri Xi}。
根据随机缺失假设, r i r_i ri在给定 X i \boldsymbol{X}_i Xi的条件下服从伯努利分布,即 r i ∣ X i ∼ B ( π i ) r_i \mid \boldsymbol{X}_i \sim \text{B}(\pi_i) ri∣Xi∼B(πi)。因此,
E { r i ∣ X i } = π i E\left\{\left. r_i \right| \boldsymbol{X}_i \right\} = \pi_i E{ri∣Xi}=πi
于是,
E { r i π i ∣ X i } = E { r i ∣ X i } π i = π i π i = 1 E\left\{\left.\frac{r_i}{\pi_i} \right| \boldsymbol{X}_i\right\} = \frac{E\left\{\left. r_i \right| \boldsymbol{X}_i \right\}}{\pi_i} = \frac{\pi_i}{\pi_i} = 1 E{πiri Xi}=πiE{ri∣Xi}=πiπi=1
因此,
E { r i π i − 1 ∣ X i } = 1 − 1 = 0 E\left\{\left.\frac{r_i}{\pi_i} - 1 \right| \boldsymbol{X}_i\right\} = 1 - 1 = 0 E{πiri−1 Xi}=1−1=0
这表明,逆概率加权调整在给定 X i \boldsymbol{X}_i Xi的条件下,平均而言是无偏的。通过这种方式,我们能够有效地处理缺失数据,减少估计偏差,提高分析的准确性。
希望这些解释能够帮助你更好地理解这些概念及其背后的数学原理。
假设 r i r_i ri 服从参数为 π i \pi_i πi 的伯努利分布:
E { r i ∣ X i } = π i E\left\{\left. r_i \right| \boldsymbol{X}_i \right\} = \pi_i E{ri∣Xi}=πi
因此,
E { r i π i ∣ X i } = 1 π i E { r i ∣ X i } = π i π i = 1 E\left\{\left. \frac{r_i}{\pi_i} \right| \boldsymbol{X}_i \right\} = \frac{1}{\pi_i} E\left\{\left. r_i \right| \boldsymbol{X}_i \right\} = \frac{\pi_i}{\pi_i} = 1 E{πiri Xi}=πi1E{ri∣Xi}=πiπi=1
由此可得,
E { r i π i − 1 ∣ X i } = 1 − 1 = 0 E\left\{\left. \frac{r_i}{\pi_i} - 1 \right| \boldsymbol{X}_i \right\} = 1 - 1 = 0 E{πiri−1 Xi}=1−1=0
这表明,逆概率加权调整项 r i π i \frac{r_i}{\pi_i} πiri 在给定 X i \boldsymbol{X}_i Xi 的条件下,其期望值为 1,因此其中心化版本 r i π i − 1 \frac{r_i}{\pi_i} - 1 πiri−1 的期望值为零。这意味着,平均而言,逆概率加权调整不会引入偏差,从而确保估计量在给定 X i \boldsymbol{X}_i Xi 的条件下保持无偏性。
总结如下:
-
随机缺失(MAR):数据的缺失仅依赖于已观测的数据,而不依赖于未观测的数据,这使得我们能够基于观测数据的概率来调整缺失数据的影响。
-
逆概率加权(IPW):通过将每个观测数据点的权重设置为其被观测概率的倒数,我们能够平衡数据,减少因缺失数据引入的偏差。
-
期望条件:逆概率加权调整项在给定 X i \boldsymbol{X}_i Xi 的情况下,平均值为 1,确保了估计的无偏性。
随机缺失意味着缺失仅依赖于已观测的数据,逆概率加权通过使用被观测概率的倒数作为权重来调整缺失数据,确保在给定 X i 的情况下,期望调整项的平均值为零,从而保证估计的无偏性。 \boxed{ \text{随机缺失意味着缺失仅依赖于已观测的数据,逆概率加权通过使用被观测概率的倒数作为权重来调整缺失数据,确保在给定 } \boldsymbol{X}_i \text{ 的情况下,期望调整项的平均值为零,从而保证估计的无偏性。} } 随机缺失意味着缺失仅依赖于已观测的数据,逆概率加权通过使用被观测概率的倒数作为权重来调整缺失数据,确保在给定 Xi 的情况下,期望调整项的平均值为零,从而保证估计的无偏性。
上面的推导我基本明白了,但是为什么期望为0就是无偏呢?无偏性难道不是估计量的期望等于真参数嘛?
无偏性通常是指估计量的期望等于真实参数值。但在这里,我们讨论的是逆概率加权调整项的期望为零,这和无偏性有什么关系呢?
让我试着理清这个逻辑。
首先,我们有一个估计量 θ ^ \hat{\theta} θ^,如果它是无偏的,那么:
E { θ ^ } = θ E\left\{ \hat{\theta} \right\} = \theta E{θ^}=θ
在这个具体的情境中,我们的目标是通过逆概率加权调整目标函数来得到一个无偏的估计量。具体来说,我们使用了加权后的目标函数:
∑ i = 1 n r i π i M \sum_{i=1}^n \frac{r_i}{\pi_i} M i=1∑nπiriM
这里的 r i π i \frac{r_i}{\pi_i} πiri 是逆概率加权调整项。我们已经证明了:
E { r i π i − 1 ∣ X i } = 0 E\left\{\left. \frac{r_i}{\pi_i} - 1 \right| \boldsymbol{X}_i \right\} = 0 E{πiri−1 Xi}=0
也就是说, r i π i \frac{r_i}{\pi_i} πiri 的期望值在给定 X i \boldsymbol{X}_i Xi 的情况下是 1。
那么,这如何保证我们的估计量是无偏的呢?
让我们考虑一下估计量的期望。假设我们的估计量是:
β ^ h = arg min β ∑ i = 1 n r i π i M \hat{\beta}_h = \arg \min_{\beta} \sum_{i=1}^n \frac{r_i}{\pi_i} M β^h=argβmini=1∑nπiriM
为了证明 β ^ h \hat{\beta}_h β^h 是无偏的,我们需要证明:
E { β ^ h } = β E\left\{ \hat{\beta}_h \right\} = \beta E{β^h}=β
直接计算这个期望可能比较复杂,但我们可以从目标函数的角度来考虑。如果调整项 r i π i \frac{r_i}{\pi_i} πiri 的期望为 1,那么在期望意义上,加权后的目标函数与未加权的目标函数是一致的:
E { ∑ i = 1 n r i π i M } = ∑ i = 1 n E { r i π i } M = ∑ i = 1 n M E\left\{ \sum_{i=1}^n \frac{r_i}{\pi_i} M \right\} = \sum_{i=1}^n E\left\{ \frac{r_i}{\pi_i} \right\} M = \sum_{i=1}^n M E{i=1∑nπiriM}=i=1∑nE{πiri}M=i=1∑nM
这表明,逆概率加权调整项在期望上没有引入额外的偏差,因此最小化加权目标函数应该能够得到与最小化真实目标函数相同的估计量,从而保证估计量的无偏性。
换句话说,虽然我们是在处理缺失数据,通过逆概率加权调整,我们确保了在期望上,估计量的行为与没有缺失数据时是一致的。因此,即使数据有缺失,估计量的期望仍然等于真实参数值,从而保证了无偏性。
总结一下:
-
逆概率加权调整项的期望为 1:这确保了加权后的目标函数在期望上与未加权的目标函数一致。
-
无偏性:因为加权目标函数的期望没有引入额外的偏差,估计量在期望上等于真实参数值。
逆概率加权调整项的期望为1,确保了加权目标函数在期望上与真实目标函数一致,从而保证了估计量的无偏性。 \boxed{ \text{逆概率加权调整项的期望为1,确保了加权目标函数在期望上与真实目标函数一致,从而保证了估计量的无偏性。} } 逆概率加权调整项的期望为1,确保了加权目标函数在期望上与真实目标函数一致,从而保证了估计量的无偏性。
这里的 π i \pi_i πi是什么意思?是指的第 i i i个样本的概率吗, 如何获得呢?
让我来解释一下 π i \pi_i πi 的含义。
在前面的讨论中, π i \pi_i πi 被定义为 r i r_i ri 为 1 的概率,即 Y i Y_i Yi 被观测到的概率。具体来说:
π i = π ( X i ) = P ( r i = 1 ∣ X i ) \pi_i = \pi(\boldsymbol{X}_i) = P(r_i = 1 \mid \boldsymbol{X}_i) πi=π(Xi)=P(ri=1∣Xi)
因此, π i \pi_i πi 表示第 i i i 个样本的 Y i Y_i Yi 被观测到的条件概率,这个概率依赖于第 i i i 个样本的协变量 X i \boldsymbol{X}_i Xi。
在随机缺失(MAR)的假设下,缺失机制仅依赖于已观测的数据 X i \boldsymbol{X}_i Xi,而不依赖于未观测的 Y i Y_i Yi。这使得 π i \pi_i πi 可以基于 X i \boldsymbol{X}_i Xi 来建模和估计,从而允许我们使用逆概率加权等方法来调整缺失数据的影响。
总结一下, π i \pi_i πi 是第 i i i 个样本的 Y i Y_i Yi 被观测到的概率,具体为:
π i = P ( r i = 1 ∣ X i ) \boxed{ \pi_i = P(r_i = 1 \mid \boldsymbol{X}_i) } πi=P(ri=1∣Xi)
相关文章:

【初识扫盲】逆概率加权
我们正在处理一个存在缺失数据的回归模型,并且希望采用一种非参数的逆概率加权方法来调整估计,以应对这种缺失数据的情况。 首先,我们需要明确问题的背景。我们有样本 { ( Y i , X i , r i ) : i 1 , … , n } \left\{\left(Y_i, \boldsym…...

Ubuntu中双击自动运行shell脚本
方法1: 修改文件双击反应 参考: https://blog.csdn.net/miffywm/article/details/103382405 chmod x test.sh鼠标选中待执行文件,在窗口左上角edit菜单中选择preference设计双击执行快捷键,如下图: 方法2: 设置一个应用 参考: https://blo…...

理解AJAX与Axios:异步编程的世界
理解AJAX与Axios:异步编程的世界 在现代Web开发中,异步编程作为一种处理复杂操作的方式,已经成为不可或缺的一部分。AJAX(Asynchronous JavaScript and XML)和Axios是两种实现异步请求的流行技术。本文将深入探讨这两…...

分组通道自注意力G-CSA详解及代码复现
G-CSA定义 G-CSA (Grouped Channel Self-Attention) 是一种创新性的视觉注意力机制,巧妙地结合了卷积和自注意力的优势。通过将输入特征图划分为多个独立的通道组,在每个组内执行自注意力操作,G-CSA实现了高效的全局信息交互,同时保留了局部特征细节。这种方法不仅提高了模…...

汽车基础软件AutoSAR自学攻略(四)-AutoSAR CP分层架构(3) (万字长文-配21张彩图)
汽车基础软件AutoSAR自学攻略(四)-AutoSAR CP分层架构(3) (万字长文-配21张彩图) 前面的两篇博文简述了AutoSAR CP分层架构的概念,下面我们来具体到每一层的具体内容进行讲解,每一层的每一个功能块力求用一个总览图,外加一个例子的图给大家进…...

玩转大语言模型——langchain调用ollama视觉多模态语言模型
系列文章目录 玩转大语言模型——ollama导入huggingface下载的模型 玩转大语言模型——langchain调用ollama视觉多模态语言模型 langchain调用ollama视觉多模态语言模型 系列文章目录前言使用Ollama下载模型查找模型下载模型 测试模型ollama测试langchain测试加载图片加载模型…...

Github 2025-01-11 Rust开源项目日报 Top10
根据Github Trendings的统计,今日(2025-01-11统计)共有10个项目上榜。根据开发语言中项目的数量,汇总情况如下: 开发语言项目数量Rust项目10C项目1Swift项目1Yazi - 快速终端文件管理器 创建周期:210 天开发语言:Rust协议类型:MIT LicenseStar数量:5668 个Fork数量:122…...

【学习】【记录】【分享】微型响应系统
前言 本篇博客源于对Vue和React框架中响应式系统的好奇与探索。若文中存在任何错误或有更优的解决方案,欢迎各位读者不吝指正,让我们一起学习,共同进步。 1. 什么是响应式系统 响应式系统是一种编程范式,它允许数据的变化自动地…...

vue城市道路交通流量预测可视化系统
文章结尾部分有CSDN官方提供的学长 联系方式名片 文章结尾部分有CSDN官方提供的学长 联系方式名片 关注B站、收藏、不迷路! 项目亮点 编号:R09 🚇 网站大屏管理三大前端、vuespringbootmysql、前后端分离架构 🚇 流量预测道路查询…...

Windows7 Emacs设置及中文乱码解决
个人博客地址:Windows7 Emacs设置及中文乱码解决 | 一张假钞的真实世界 环境说明 Windows7GNU Emacs 25.1.1安装路径:D:/apps/emacs/ 配置Emacs 在Windows7下安装完Emacs后,默认情况下Emacs不会在一启动的时候就生成.emacs配置文件和.ema…...
高级算法C5.0决策树算法介绍)
Python AI教程之十五:监督学习之决策树(6)高级算法C5.0决策树算法介绍
C5.0决策树算法 C5 算法由 J. Ross Quinlan 创建,是 ID3 决策树方法的扩展。它通过根据信息增益(衡量通过按特定属性进行划分而实现的熵减少量)递归地划分数据来构建决策树。 对于分类问题,C5.0 方法是一种决策树算法。它构建规则集或决策树,这是对 C4.5 方法的改进。根…...

MOS管为什么会有夹断,夹断后为什么会有电流?该电流为什么是恒定的?
以下是对MOS管MOS管为什么会有夹断,夹断后为什么还会有电流?该电流为什么是恒定的?的一些心得体会。 1. MOS管为什么会有夹断? 可以认为D极加压使得D极的耗尽层增大(原因是N极接正极,P极接负极,电子被吸引…...
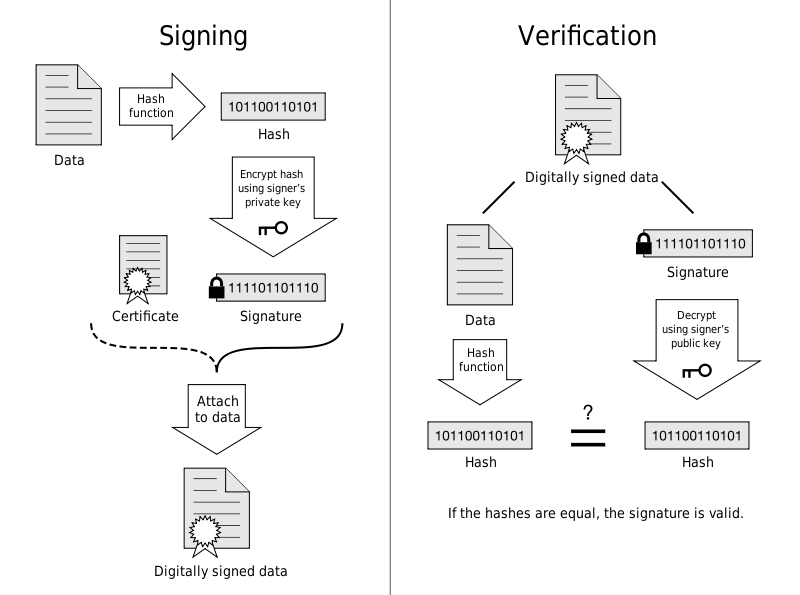
网络安全-RSA非对称加密算法、数字签名
数字签名非常普遍: 了解数字签名前先了解一下SHA-1摘要,RSA非对称加密算法。然后再了解数字签名。 SHA-1 SHA-1(secure hash Algorithm )是一种 数据加密算法。该算法的思想是接收一段明文,然后以一种不可逆的方式将…...

【AI日记】25.01.13
【AI论文解读】【AI知识点】【AI小项目】【AI战略思考】【AI日记】【读书与思考】 AI kaggle 比赛:Forecasting Sticker Sales 读书 书名:罗素论幸福 律己 AI: 8 小时,良作息:1:00-9:00, 良短视频&…...

Mysql--运维篇--空间管理(表空间,索引空间,临时表空间,二进制日志,数据归档等)
MySQL的空间管理是指对数据库存储资源的管理和优化。确保数据库能够高效地使用磁盘空间、内存和其他系统资源。良好的空间管理不仅有助于提高数据库的性能,还能减少存储成本并防止因磁盘空间不足导致的服务中断。MySQL的空间管理涉及多个方面,包括表空间…...

JVM面试相关
JVM组成 什么是程序计数器 详细介绍Java堆 什么是虚拟机栈 能不能解释一下方法区? 直接内存相关 类加载器 什么是类加载器,类加载器有哪些 什么是双亲委派模型 类加载过程 垃圾回收 对象什么时候可以被垃圾回收器回收 JVM垃圾回收算法有那些 JVM的分代…...

【leetcode 13】哈希表 242.有效的字母异位词
原题链接 题解链接 一般哈希表都是用来快速判断一个元素是否出现集合里。 当我们想使用哈希法来解决问题的时候,我们一般会选择如下三种数据结构。 数组 set (集合) map(映射) 如果在做面试题目的时候遇到需要判断一个元素是否出现过的场景…...

Blazor开发复杂信息管理系统的优势
随着现代企业信息管理需求的不断提升,开发高效、易维护、可扩展的系统变得尤为重要。在这个过程中,Blazor作为一种新兴的Web开发框架,因其独特的优势,逐渐成为开发复杂信息管理系统的首选技术之一。本文将结合Blazor在开发复杂信息…...

ue5 1.平A,两段连击蒙太奇。鼠标点一下,就放2段动画。2,动画混合即融合,边跑边挥剑,3,动画通知,动画到某一帧,把控制权交给蓝图。就执行蓝图节点
新建文件夹 创建一个蒙太奇MA_Melee 找到c_slow 调节一下速度 把D_slow拖上去 中间加一个片段 哎呀呀,写错了,我想写2 把这个标记拖过来,点击默认default 弄第二个片段 就会自己变成这个样子 把2这个标记拖到中间 鼠标左键&a…...

2025,AI走向何方?暴雨技术专家为您展望
过去一年中,人工智能技术飞速发展,在各行各业都收获了巨大进展。面对即将到来的2025年,暴雨技术研发团队的专家对AI领域的发展趋势进行了展望,让我们来看看未来一年,有哪些重要趋势值得关注。 迈向关键转折的一步 20…...

Vim 调用外部命令学习笔记
Vim 外部命令集成完全指南 文章目录 Vim 外部命令集成完全指南核心概念理解命令语法解析语法对比 常用外部命令详解文本排序与去重文本筛选与搜索高级 grep 搜索技巧文本替换与编辑字符处理高级文本处理编程语言处理其他实用命令 范围操作示例指定行范围处理复合命令示例 实用技…...

TDengine 快速体验(Docker 镜像方式)
简介 TDengine 可以通过安装包、Docker 镜像 及云服务快速体验 TDengine 的功能,本节首先介绍如何通过 Docker 快速体验 TDengine,然后介绍如何在 Docker 环境下体验 TDengine 的写入和查询功能。如果你不熟悉 Docker,请使用 安装包的方式快…...

盘古信息PCB行业解决方案:以全域场景重构,激活智造新未来
一、破局:PCB行业的时代之问 在数字经济蓬勃发展的浪潮中,PCB(印制电路板)作为 “电子产品之母”,其重要性愈发凸显。随着 5G、人工智能等新兴技术的加速渗透,PCB行业面临着前所未有的挑战与机遇。产品迭代…...

Java 8 Stream API 入门到实践详解
一、告别 for 循环! 传统痛点: Java 8 之前,集合操作离不开冗长的 for 循环和匿名类。例如,过滤列表中的偶数: List<Integer> list Arrays.asList(1, 2, 3, 4, 5); List<Integer> evens new ArrayList…...
:滤镜命令)
ffmpeg(四):滤镜命令
FFmpeg 的滤镜命令是用于音视频处理中的强大工具,可以完成剪裁、缩放、加水印、调色、合成、旋转、模糊、叠加字幕等复杂的操作。其核心语法格式一般如下: ffmpeg -i input.mp4 -vf "滤镜参数" output.mp4或者带音频滤镜: ffmpeg…...

pikachu靶场通关笔记22-1 SQL注入05-1-insert注入(报错法)
目录 一、SQL注入 二、insert注入 三、报错型注入 四、updatexml函数 五、源码审计 六、insert渗透实战 1、渗透准备 2、获取数据库名database 3、获取表名table 4、获取列名column 5、获取字段 本系列为通过《pikachu靶场通关笔记》的SQL注入关卡(共10关࿰…...

Spring数据访问模块设计
前面我们已经完成了IoC和web模块的设计,聪明的码友立马就知道了,该到数据访问模块了,要不就这俩玩个6啊,查库势在必行,至此,它来了。 一、核心设计理念 1、痛点在哪 应用离不开数据(数据库、No…...

如何理解 IP 数据报中的 TTL?
目录 前言理解 前言 面试灵魂一问:说说对 IP 数据报中 TTL 的理解?我们都知道,IP 数据报由首部和数据两部分组成,首部又分为两部分:固定部分和可变部分,共占 20 字节,而即将讨论的 TTL 就位于首…...

稳定币的深度剖析与展望
一、引言 在当今数字化浪潮席卷全球的时代,加密货币作为一种新兴的金融现象,正以前所未有的速度改变着我们对传统货币和金融体系的认知。然而,加密货币市场的高度波动性却成为了其广泛应用和普及的一大障碍。在这样的背景下,稳定…...

视觉slam十四讲实践部分记录——ch2、ch3
ch2 一、使用g++编译.cpp为可执行文件并运行(P30) g++ helloSLAM.cpp ./a.out运行 二、使用cmake编译 mkdir build cd build cmake .. makeCMakeCache.txt 文件仍然指向旧的目录。这表明在源代码目录中可能还存在旧的 CMakeCache.txt 文件,或者在构建过程中仍然引用了旧的路…...
