二叉树(了解)c++
二叉树是一种特殊的树型结构,它的特点是:
- 每个结点至多只有2棵子树(即二叉树中不存在度大于2的结点)
- 并且二叉树的子树有左右之分,其次序不能任意颠倒,因此是一颗有序树
以A结点为例,左边的B是它的左孩子,右边的C是它的右孩子,以左孩子为根的这棵树称为左指树,以右孩子为根的这棵树称为右子树,把BDEH单独拉出来看就是一个二叉树,B是它的根结点,D H是左子树,E是右子树,同理,C这个右子树也是把CFGI单独拿出来看,C是他的根结点,FI是左子树,G是右子树,因此二叉树可以抽象为右边这个等式

- 二叉树也是通过递归定义的结构
满二叉树:
在一棵二叉树中,所有非叶结点都存在左右孩子,所有叶子结点都在同一层,那么这棵树就是满二叉树

性质:
- 高度为h的满二叉树,结点个数为2h-1
- 结点个数为n的满二叉树,树高h=log以2为底n+1
- 如果将满二叉树按照层序遍历的过程编号:从根节点开始,由1开始编号:
- 结点i左孩子的编号为2xi
- 结点i右孩子的编号为2xi+1结点i双亲的编号为i/2
- 这个性质可以帮助我们存储二叉树
完全二叉树
如果一棵树所有结点和同样深度的满二叉树,按照层序遍历编号的位置-一对应,则这棵二叉树为完全二叉树。(这个定义很抽象,我们可以记住相当于在满二叉树的基础上,从后往前依次删掉一些结点就变成了完全二叉树 )

相关文章:

二叉树(了解)c++
二叉树是一种特殊的树型结构,它的特点是: 每个结点至多只有2棵子树(即二叉树中不存在度大于2的结点) 并且二叉树的子树有左右之分,其次序不能任意颠倒,因此是一颗有序树 以A结点为例,左边的B是它的左孩子,右边的C是…...

备赛蓝桥杯之第十五届职业院校组省赛第三题:产品360度展示
提示:本篇文章仅仅是作者自己目前在备赛蓝桥杯中,自己学习与刷题的学习笔记,写的不好,欢迎大家批评与建议 由于个别题目代码量与题目量偏大,请大家自己去蓝桥杯官网【连接高校和企业 - 蓝桥云课】去寻找原题࿰…...

业余无线电 对讲机常用频率使用
我自己的总结是,基本可以无忧使用: 144.035-145.800 146.000-148.000 430.000-431.900 432.240-435.000 438.000-439.000 50Mhz一般手台不支持,暂不记录。 以下为附录可以自行阅读,本文内容如有错误请留言指正。 特定波段…...

个性化的语言模型构建思路
将开源模型(如Llama3、Qwen、Falcon3 … 等)转变为个人专属的大语言模型,通常涉及知识库的构建、微调(fine-tuning)和模型定制等步骤。下面提供一个详细的技术解决方案,涵盖了如何利用现有的资料(如文档、PDF、Excel、PPT、图片、语音、视频等)将开源模型转换为个人专属…...

QT开发技术【QFileDialog卡顿问题】
一、直接用QFileDialog 在window 一般卡顿7秒 qDebug() << "begin:" << QDateTime::currentDateTime().toString("yyyy-MM-dd hh:mm:ss.zzz");QDateTime sTime QDateTime::currentDateTime();QString str QFileDialog::getOpenFileName(null…...
和nextLine()不能混用 | nextInt()和nextInt()之类的可以一起用)
关于为什么java中nextInt()和nextLine()不能混用 | nextInt()和nextInt()之类的可以一起用
键盘录入的区别: 第一套体系:遇到空格、制表符、回车都结束,并且都不接收 nextInt()、nextDouble()、next() 遇到空格、制表符、回车就结束,只接收其之前的数据,空格以及空格之后的数据都在缓冲区内,如果…...

Android OpenGL(六) 纹理
纹理 纹理是一个2D图片(甚至也有1D和3D的纹理), 它可以用来添加物体的细节;你可以想象纹理是一张绘有砖块的纸,无缝折叠贴合到你的3D的 房子上,这样你的房子看起来就像有砖墙外表了 纹理环绕方式 纹理坐…...

git和idea重新安装后提交异常
场景:我重装了系统,idea装了2024.3版本的,git也重新装了,但是项目中还是有.git文件夹的,下载了idea的码云插件后,提交报错如下: 异常:Error updating changes: detected dubious ow…...

leetcode刷题记录(八十一)——236. 二叉树的最近公共祖先
(一)问题描述 236. 二叉树的最近公共祖先 - 力扣(LeetCode)236. 二叉树的最近公共祖先 - 给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。百度百科 [https://baike.baidu.com/item/%E6%9C%80%E8%BF%91%E5%85%AC%E5%85%B…...

STM32-CAN总线
1.CAN总线简介 CAN总线是由BOSCH公司开发的一种简洁易用、传输速度快、易扩展、可靠性高的串行通信总线 2.CAN总线特征 两根通信线(CAN_H、CAN_L),线路少,无需共地差分信号通信(相对的是单端信号)&#…...

node.js 07.npm下包慢的问题与nrm的使用
一.npm下包慢 因为npm i 默认从npm官网服务器进行下包,但是npm官网服务器是海外服务器所以响应很慢. 于是我们通过npm下包的时候通常用淘宝镜像进行下包,下面是切换到淘宝镜像地址下包的操作. 二.nrm的使用 nrm是一个管理切换npm下包地址的工具,可以快速切换下包的地址. 安…...

ubuntu改变swap存储空间,遇到 fallocate 失败: 文本文件忙
ubuntu改变swap存储空间,遇到 fallocate 失败: 文本文件忙 sudo fallocate -l 16G /swapfile fallocate: fallocate 失败: 文本文件忙这种情况是swap空间正在使用,需要先关闭swap分区: sudo swapoff /swapfile sudo fallocate -l 16G /swap…...

20250122-正则表达式
1. 正则标记 表示一位字符:\\ 表示指定的一位字符:x 表示任意的一位字符:. 表示任意一位数字:\d 表示任意一位非数字:\D 表示任意一个字母:[a-zA-Z](大写或小写) 表示任意一个…...

QT之CMAKE教程
介绍 CMake 是一个跨平台的自动化构建系统,它使用配置文件(称为 CMakeLists.txt)来生成标准的构建文件,如 Unix 的 Makefile 或 Windows 的 Visual Studio 工程文件。CMake 能够支持多种编程语言,尤其是 C 和 C&#…...

网络安全 | 0day漏洞介绍
关注:CodingTechWork 引言 在网络安全领域,0day漏洞(Zero-day Vulnerability)是指一个尚未被厂商、开发者或安全人员发现、修复或发布修补程序的安全漏洞。0day漏洞是黑客利用的一个重要攻击工具,因其未被披露或未被修…...
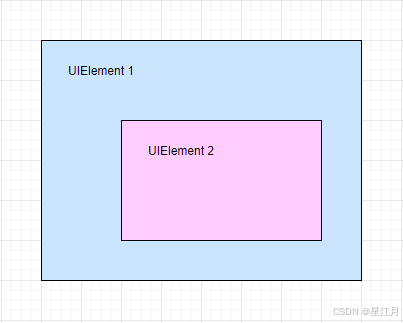
关于WPF中ComboBox文本查询功能
一种方法是使用事件(包括MVVM的绑定) <ComboBox TextBoxBase.TextChanged"ComboBox_TextChanged" /> 然而运行时就会发现,这个事件在疯狂的触发,很频繁 在实际应用中,如果关联查询数据库࿰…...

07_游戏加载窗口
隐藏动态提示窗口 创建空节点 命名为 LoadingWnd 意为加载窗口 并设置全屏 在子级下创建Image作为加载背景 也设置成全屏 将以下资源放进Art文件夹中 设置好精灵模式后拖拽至 Image的Source Image框选 创建文本作为提示内容 增加描边组件OutLine可以美化字体 创建Image作为加载…...

awk命令进阶
1.连接文件 awk NRFNR{a[$1]$0;next} NR!FNR{ if(($5) in a) print a[$1],$0 } file1 file2 命令详解: 这个命令的目的是将 file1 和 file2 基于某个共同字段进行连接(类似于 SQL 中的 JOIN 操作)。下面我们逐步解析它的工作原理。 1. NRF…...

解锁Java中的国密算法:安全保障的密钥
一、引言 在数字化浪潮席卷全球的当下,信息安全已然成为国家、企业乃至个人无法忽视的重要议题。国密算法,作为我国自主研发的密码算法体系,宛如坚固的盾牌,为国家信息安全筑起了一道坚不可摧的防线。它的诞生,不仅承载…...

基于迁移学习的ResNet50模型实现石榴病害数据集多分类图片预测
完整源码项目包获取→点击文章末尾名片! 番石榴病害数据集 背景描述 番石榴 (Psidium guajava) 是南亚的主要作物,尤其是在孟加拉国。它富含维生素 C 和纤维,支持区域经济和营养。不幸的是,番石榴生产受到降…...

Python爬虫实战:研究MechanicalSoup库相关技术
一、MechanicalSoup 库概述 1.1 库简介 MechanicalSoup 是一个 Python 库,专为自动化交互网站而设计。它结合了 requests 的 HTTP 请求能力和 BeautifulSoup 的 HTML 解析能力,提供了直观的 API,让我们可以像人类用户一样浏览网页、填写表单和提交请求。 1.2 主要功能特点…...

第19节 Node.js Express 框架
Express 是一个为Node.js设计的web开发框架,它基于nodejs平台。 Express 简介 Express是一个简洁而灵活的node.js Web应用框架, 提供了一系列强大特性帮助你创建各种Web应用,和丰富的HTTP工具。 使用Express可以快速地搭建一个完整功能的网站。 Expre…...

UE5 学习系列(三)创建和移动物体
这篇博客是该系列的第三篇,是在之前两篇博客的基础上展开,主要介绍如何在操作界面中创建和拖动物体,这篇博客跟随的视频链接如下: B 站视频:s03-创建和移动物体 如果你不打算开之前的博客并且对UE5 比较熟的话按照以…...
可以参考以下方法:)
根据万维钢·精英日课6的内容,使用AI(2025)可以参考以下方法:
根据万维钢精英日课6的内容,使用AI(2025)可以参考以下方法: 四个洞见 模型已经比人聪明:以ChatGPT o3为代表的AI非常强大,能运用高级理论解释道理、引用最新学术论文,生成对顶尖科学家都有用的…...

ip子接口配置及删除
配置永久生效的子接口,2个IP 都可以登录你这一台服务器。重启不失效。 永久的 [应用] vi /etc/sysconfig/network-scripts/ifcfg-eth0修改文件内内容 TYPE"Ethernet" BOOTPROTO"none" NAME"eth0" DEVICE"eth0" ONBOOT&q…...

【FTP】ftp文件传输会丢包吗?批量几百个文件传输,有一些文件没有传输完整,如何解决?
FTP(File Transfer Protocol)本身是一个基于 TCP 的协议,理论上不会丢包。但 FTP 文件传输过程中仍可能出现文件不完整、丢失或损坏的情况,主要原因包括: ✅ 一、FTP传输可能“丢包”或文件不完整的原因 原因描述网络…...
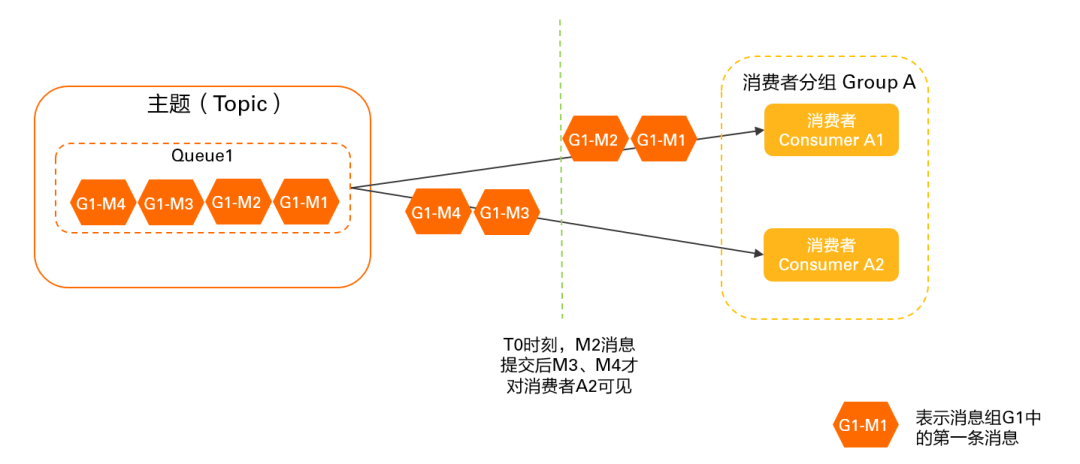
RocketMQ 客户端负载均衡机制详解及最佳实践
延伸阅读:🔍「RocketMQ 中文社区」 持续更新源码解析/最佳实践,提供 RocketMQ 专家 AI 答疑服务 前言 本文介绍 RocketMQ 负载均衡机制,主要涉及负载均衡发生的时机、客户端负载均衡对消费的影响(消息堆积/消费毛刺等…...

OCC笔记:TDF_Label中有多个相同类型属性
注:OCCT版本:7.9.1 TDF_Label中有多个相同类型的属性的方案 OCAF imposes the restriction that only one attribute type may be allocated to one label. It is necessary to take into account the design of the application data tree. For exampl…...

Python 解释器安装全攻略(适用于 Linux / Windows / macOS)
目录 一、Windows安装Python解释器1.1 下载并安装Python解释1.2 测试安装是否成功1.3 设置pip的国内镜像------永久配置 二、macOS安装Python解释器三、Linux下安装Python解释器3.1 Rocky8.10/Rocky9.5安装Python解释器3.2 Ubuntu2204/Ubuntu2404安装Python解释器3.3 设置pip的…...
shellcode混淆uuid/ipv6/mac)
【免杀】C2免杀技术(十五)shellcode混淆uuid/ipv6/mac
针对 shellcode 混淆(Shellcode Obfuscation) 的实战手段还有很多,如下表所示: 类型举例目的编码 / 加密XOR、AES、RC4、Base64、Poly1305、UUID、IP/MAC改变字节特征,避开静态签名或 YARA结构伪装PE Stub、GIF/PNG 嵌入、RTF OLE、UUID、IP/MAC看起来像合法文件/数据,弱…...
