【数据结构进阶】红黑树超详解 + 实现(附源码)
🌟🌟作者主页:ephemerals__
🌟🌟所属专栏:数据结构
目录
前言
一、红黑树介绍
二、红黑树原理详解
三、红黑树的实现
1. 节点定义
2. 红黑树类型定义及接口声明
3. 红黑树的插入(重点)
颜色设置
平衡调整
总代码
4. 红黑树的查找
5. 中序遍历、拷贝构造和析构
6. 检查红黑树是否合法
7. 程序全部代码
总结
前言
在传统二叉搜索树的基础上,我们学习了AVL树,它通过独特的平衡机制,确保了稳定高效的插入、查找和删除操作。然而,由于其频繁的平衡调整,可能使性能收到一定影响。因此,另一种自平衡二叉搜索树——红黑树应运而生。本篇文章,我们将深入探讨红黑树的实现原理,带你解开其简洁而深邃的设计之美。
与AVL树相同,之后的红黑树实现当中,我们会将键值对(pair)作为节点数据域。
如果你不是很了解二叉搜索树、AVL树或pair,可以参阅这两篇文章:
【数据结构】二叉搜索树(二叉排序树)-CSDN博客
【数据结构进阶】AVL树深度剖析 + 实现(附源码)-CSDN博客
注:若无特殊说明,本文所提到的所有“路径”都指根节点到NULL的路径。
一、红黑树介绍
红黑树(Red-Black-Tree)是一种自平衡二叉搜索树,但它并非像AVL树那样“严格平衡”,而是允许一定的不平衡存在,在保证增删查改效率没有太大影响的情况下,显著减少了平衡调整的次数,提升总体效率。
AVL树一般通过节点的“平衡因子”来维持平衡,而红黑树通过给节点“着色”,确保其高效性。
在非空情况下,红黑树的性质(约束条件)如下:
1. 它是一棵二叉搜索树
2. 每一个节点都会被着色,不是黑色就是红色
3. 根节点必须为黑色
4. 对于一个红色节点,它的孩子或为空,或是黑色。也就是说路径上不能有连续红色节点
5. 从根节点到NULL节点的所有路径上,黑色节点的数量都相同
有了以上约束条件,就可确保其没有一条路径长度能够超出其他路径的2倍,从而保证高效操作。

如上图,每一条路径上都有相同数量的黑色节点。
二、红黑树原理详解
那么,红黑树为什么能够控制路径长度呢?
来看一个极端情况:
假设一棵红黑树的一条路径上有n个黑色节点,那么由于其所有路径上的黑色节点数量是相同的,所以其所有路径上都一定有n个黑色节点。对于这棵树,最长的可能路径上的节点就是一黑一红一黑一红(要确保无连续红色节点)......一共有2n个节点;最短的可能路径上的节点是全黑的,一共有n个节点。那么其他可能的路径长度都在n~2n之间。所以说没有一条路径长度能够超出其他路径长度的两倍,也就确保了根节点左右子树的高度比一定在1~2之间。

接下来,我们分析一下红黑树的效率。
设一棵红黑树一共有N个节点,它的最短可能路径的长度为h,由于可能的路径长度都在h~2h之间,那么节点数N就满足 。由此可知,在路径最短情况下,其进行增删查改的时间消耗为O(logN);路径最长情况下,进行查找的时间消耗为O(2logN)。因此红黑树增删查改的时间复杂度为O(logN)。

红黑树的平衡控制相对AVL树较为抽象,但由于那几点约束条件,控制了最长路径和最短路径之比,间接地使红黑树达到了“近似平衡”,增删查改地时间消耗不会过大,并且相比AVL树,旋转调整次数会更少。
三、红黑树的实现
1. 节点定义
红黑树节点及其颜色定义如下:
enum Color//枚举值表示颜色
{RED,BLACK
};//节点
template<class K, class V>
struct RBTreeNode
{pair<K, V> _kv;//数据域RBTreeNode<K, V>* _left;//指向左孩子的指针RBTreeNode<K, V>* _right;//指向右孩子的指针RBTreeNode<K, V>* _parent;//指向父亲的指针Color _col;//颜色RBTreeNode(const pair<K, V>& kv)//节点构造:_kv(kv), _left(nullptr), _right(nullptr), _parent(nullptr){}
};与AVL树相同,红黑树也采用三叉链表结构,更有利于节点之间的控制访问。
在节点构造当中,我们并没有设置节点的初始颜色,之后在实现节点插入的实现当中,我们会重点讨论初始颜色的问题。
2. 红黑树类型定义及接口声明
我们需要实现的接口如下:
//红黑树类
template<class K, class V>
class RBTree
{typedef RBTreeNode<K, V> Node;
public://强制生成无参构造RBTree() = default;//拷贝构造RBTree(const RBTree<K, V>& t);//析构函数~RBTree();//插入bool Insert(const pair<K, V>& kv);//查找Node* Find(const K& key);//中序遍历void Inorder();//判断是否为合法红黑树bool IsValidRBTree();
private:Node* _root = nullptr;//根节点指针
};3. 红黑树的插入(重点)
为了保持红黑树增删查改的高效性,插入操作要保证满足红黑树的性质。
红黑树的插入过程大致如下:
1. 首先按照二叉搜索树的插入规则确定插入节点的位置。
2. 插入新节点,并确定新节点的颜色。
3. 为保持红黑树的性质,需要对原有树结构进行平衡调整。
颜色设置
我们首先来探讨新节点的颜色设置问题。
如果新插入的节点是根节点(树为空),毋庸置疑,为黑色。并且此时整个结构已经满足红黑树性质,插入完成。
如果新插入的节点不是根节点,那么能否设置初始颜色为黑色呢?我们假设新插入的节点为黑色:

不难发现,插入节点4之后,已经不满足红黑树性质:5->2->4->NULL这条路径上有3个黑色节点,而5->7->6->NULL这条路径上有2个黑色节点。实际上,如果插入黑色节点,不管插入到什么位置,该条路径上的黑色节点数都会增加,而其他路径上的黑色节点数不变,此时一定会违反红黑树的约束条件。
那么,我们插入一个红色节点:

此时可以看到,插入之后,整个结构依然满足红黑树的性质。当然,这是因为节点2是黑色节点,此时插入结束。若一个红色节点插入在红色节点的下方,出现连续红色节点,那么也会违反约束条件。
总之,若插入黑色节点,一定违反红黑树规则,而插入红色节点,可能违反红黑树规则。所以我们退而求其次,将新节点(除根节点外)设置为红色。
平衡调整
确定了新节点颜色之后,我们探讨平衡调整的问题。
之前已经提到,我们如果将新节点插入在红色节点的下方,就需要进行平衡调整。有两种情况需要分别讨论。

情况1:仅变色

如上图所示, parent和uncle都是红色,grandfather为黑色,此时插入新节点cur,出现连续红色节点。这种情况下,将parent和uncle变黑,grandfather变红,整个结构就满足了红黑树的性质。
但上图是一种具体情况,如果整棵树是另一棵树的子树,且节点4是红色的,那么变色之后就会再次出现连续的红色节点(节点2和节点4),此时就需要继续向上调整:将grandfather作为新的cur,然后找到新的parent和uncle,进行变色或做其他调整(之后会讲解),然后再向上检查,直到遇到根节点或者无连续红色节点为止。
通过观察上图,不难发现:针对需要进行平衡调整的情况,新节点插入之后,parent一定为红,否则无需调整;grandfather一定为黑,否则未插入节点时就已经出现连续红色节点,红黑树原本就有问题。 那么,重要变量就是uncle节点。
总结:当uncle为红时,仅需变色:将parent和uncle变黑,grandfather变红。然后将grandfather作为新的cur,找到新的parent和uncle,继续判断、调整,直到遇到根节点或无连续红色节点。
情况2:旋转+变色
刚才提到uncle是重要变量,那么我们就给出uncle的其他可能情况(不存在或为黑),进而分析各种调整场景。
分类讨论之前,我们首先需要明确需要进行平衡调整的情况下,uncle和cur的关系。
一个节点被标记为cur(确定插入位置之后),仅有两种情况:
1. 它是新增节点;2. 它是场景1向上调整时标记的节点。
当uncle不存在时,cur一定是新增节点。原因:若cur不是新增节点,则其必然是向上调整时标记的节点,那么一定发生了变色,也就是说cur所在的某条路径A上至少有两个黑色节点(包括一个根节点)。而uncle不存在,则从根节点到uncle(NULL)位置的路径上的黑色节点数一定少于路径A,两条路径黑色节点数量不一致,不满足红黑树性质。
当uncle为黑时,cur一定时向上调整时标记的节点。原因:uncle为黑,则从根节点到uncle的路径B上至少有两个黑色节点。如果cur是新增节点,那么从根节点到cur的路径上的黑色节点数一定少于路径B,两条路径黑色节点数量不一致,不满足红黑树性质。
uncle不存在:

这种情况下,如果只是改变parent和grandfather的颜色,并不能解决问题:变色之后路径4->2->1->NULL上有1个黑色节点,而路径4->NULL上没有黑色节点,不满足红黑树性质。
此时就要配合旋转操作来解决问题。根据三个节点的相对位置,需要我们分情况进行单旋或双旋,从而调整树的结构:
单旋+变色:

可以看到,我们以grandfather为旋转点,进行右/左单旋,然后将parent变黑,grandfather变红,整个结构满足红黑树性质,并且该部分的根已经变成黑色,无需继续向上调整,插入结束。
双旋+变色:

双旋完成后,将cur变黑,grandfather变红,整个结构满足红黑树,并且该部分的根已经变成黑色,无需继续向上调整,插入结束。
总结:当uncle不存在时,需要根据实际情况进行旋转+变色。单旋完成后要将parent变黑,grandfather变红;双旋完成后要将cur变黑,grandfather变红。操作结束后,该部分的根成为黑色,不会出现连续红色节点,无需再向上调整。
uncle为黑:
刚才已经提到,uncle为黑时,cur一定是向上调整时标记的节点。所以我们使用抽象图来表示插入状况:

如图所示, a、b、c、d、e分别表示相应黑色节点数量的子树,当a、b的黑色节点数由n-1变为n时,说明发生了变色,使得cur变为红色。此时由于uncle是黑色,如果直接将parent变黑,grandfather变红,那么根节点到a、b、c路径上的黑色节点数与到d、e的路径不相等,不满足红黑树的性质。所以要以grandfather为旋转点,分情况进行旋转再变色。
不难发现,uncle为黑时的旋转、变色逻辑与uncle不存在时完全相同,这里博主就不再一一列举各种旋转情况。总结:当uncle为黑时,需要根据实际情况进行旋转+变色。单旋完成后要将parent变黑,grandfather变红;双旋完成后要将cur变黑,grandfather变红。操作结束后,该部分的根成为黑色,不会出现连续红色节点,无需再向上调整。
注意:平衡调整完成之后,整棵树的根节点可能变为红色。所以平衡调整结束后,一定要将根节点设置为黑色。
红黑树插入的总体过程:

总代码
红黑树插入代码实现:
//插入
bool Insert(const pair<K, V>& kv)
{if (_root == nullptr)//树为空,直接插入{_root = new Node(kv);_root->_col = BLACK;return true;}//先查找合适的插入位置Node* parent = nullptr;Node* cur = _root;while (cur){if (kv.first < cur->_kv.first){parent = cur;cur = cur->_left;}else if (kv.first > cur->_kv.first){parent = cur;cur = cur->_right;}else{return false;}}cur = new Node(kv);cur->_col = RED;//插入红色节点if (kv.first < parent->_kv.first){parent->_left = cur;}else{parent->_right = cur;}cur->_parent = parent;//parent为红,进行平衡调整while (parent && parent->_col == RED){//确定grandfatherNode* grandfather = parent->_parent;if (parent == grandfather->_left){//确定uncleNode* uncle = grandfather->_right;if (uncle && uncle->_col == RED)//uncle为红,仅变色{parent->_col = uncle->_col = BLACK;grandfather->_col = RED;//继续向上判断cur = grandfather;parent = cur->_parent;}else//uncle为黑或不存在,旋转+变色{if (cur == parent->_left)//右单旋{RotateR(grandfather);//变色parent->_col = BLACK;grandfather->_col = RED;}else//左右双旋{RotateL(parent);RotateR(grandfather);//变色cur->_col = BLACK;grandfather->_col = RED;}break;//旋转完成,直接跳出循环}}else{//确定uncleNode* uncle = grandfather->_left;if (uncle && uncle->_col == RED)//uncle为红,仅变色{parent->_col = uncle->_col = BLACK;grandfather->_col = RED;//继续向上判断cur = grandfather;parent = cur->_parent;}else//uncle为黑或不存在,旋转+变色{if (cur == parent->_right)//左单旋{RotateL(grandfather);//变色parent->_col = BLACK;grandfather->_col = RED;}else//右左双旋{RotateR(parent);RotateL(grandfather);//变色cur->_col = BLACK;grandfather->_col = RED;}break;//旋转完成,直接跳出循环}}}//最后将根节点设置为黑色_root->_col = BLACK;return true;
}//右单旋
void RotateR(Node* parent)
{Node* subL = parent->_left;Node* subLR = subL->_right;parent->_left = subLR;if (subLR) subLR->_parent = parent;Node* ppNode = parent->_parent;subL->_right = parent;parent->_parent = subL;if (parent == _root){_root = subL;subL->_parent = nullptr;}else{if (ppNode->_left == parent) ppNode->_left = subL;else ppNode->_right = subL;subL->_parent = ppNode;}
}//左单旋
void RotateL(Node* parent)
{Node* subR = parent->_right;Node* subRL = subR->_left;parent->_right = subRL;if (subRL) subRL->_parent = parent;Node* ppNode = parent->_parent;subR->_left = parent;parent->_parent = subR;if (parent == _root){_root = subR;subR->_parent = nullptr;}else{if (ppNode->_left == parent) ppNode->_left = subR;else ppNode->_right = subR;subR->_parent = ppNode;}
}4. 红黑树的查找
红黑树的查找逻辑与传统二叉搜索树相同,注意按照键查找。
代码如下:
//查找
Node* Find(const K& key)
{Node* cur = _root;while (cur){if (key < cur->_kv.first){cur = cur->_left;//小了往左走}else if (key > cur->_kv.first){cur = cur->_right;//大了往右走}else{return cur;//找到了,返回}}return nullptr;//没找到,返回空指针
}5. 中序遍历、拷贝构造和析构
三个函数的实现逻辑与AVL树完全相同。注意拷贝时不要忘记parent指针。
代码如下:
//中序遍历
void Inorder()
{_Inorder(_root);
}
void _Inorder(Node* root)
{if (root == nullptr) return;_Inorder(root->_left);cout << root->_kv.first << ' ' << root->_kv.second << endl;_Inorder(root->_right);
}//拷贝构造
RBTree(const RBTree<K, V>& t)
{_root = _Copy(t._root);
}
Node* _Copy(Node* root, Node* parent = nullptr)
{if (root == nullptr) return nullptr;Node* NewRoot = new Node(root->_kv);NewRoot->_col = root->_col;//复制颜色NewRoot->_parent = parent;//设置父指针//递归拷贝左子树和右子树NewRoot->_left = _Copy(root->_left, NewRoot);NewRoot->_right = _Copy(root->_right, NewRoot);return NewRoot;
}//析构函数
~RBTree()
{_Destroy(_root);
}
void _Destroy(Node* root)
{if (root == nullptr) return;_Destroy(root->_left);_Destroy(root->_right);delete root;
}6. 检查红黑树是否合法
判断一棵红黑树是否合法,就要判断它是否满足红黑树的性质。可以从以下几点入手:
1. 检查根节点是否为黑色。
2. 当一个节点为红色时,判断其父亲是否是黑色。
3. 检查各个路径上的黑色节点数是否相等。
对于第三点,可以先遍历一条路径(可以选择走最左路径,避免递归),记录路径上的黑色节点个数,然后再判断其他所有路径上的黑色节点个数是否与之一致。
代码实现:
//判断是否为合法红黑树
bool IsValidRBTree()
{//空树,合法if (_root == nullptr) return true;//根节点为红,非法if (_root->_col == RED){cout << "根节点为红" << endl;return false;}int refNum = 0;//记录黑色节点个数Node* cur = _root;while (cur){if (cur->_col == BLACK) refNum++;cur = cur->_left;}//递归检查所有路径return _Check(_root, 0, refNum);
}//路径检查
bool _Check(Node* root, int num, const int refNum)
{if (root == nullptr){//遍历到空,进行黑色节点比较if (num != refNum){cout << "黑色节点数量不相等" << endl;return false;}return true;}//检查是否有连续红色节点if (root->_col == RED && root->_parent->_col == RED){cout << "有连续红色节点" << endl;return false;}//记录当前路径的黑色节点数if (root->_col == BLACK) num++;//递归检查左子树和右子树return _Check(root->_left, num, refNum) && _Check(root->_right, num, refNum);
}接下来我们写一段代码,插入一组数据,验证红黑树的合法性:
int main()
{RBTree<int, int> t;int a[] = { 4, 2, 6, 1, 3, 5, 15, 7, 16, 14 };for (auto& e : a){t.Insert({ e,e });}t.Inorder();cout << t.IsValidRBTree() << endl;return 0;
}运行结果:

7. 程序全部代码
红黑树实现全部代码如下:
#include <iostream>
#include <utility>
using namespace std;enum Color//枚举值表示颜色
{RED,BLACK
};//节点
template<class K, class V>
struct RBTreeNode
{pair<K, V> _kv;//数据域RBTreeNode<K, V>* _left;//指向左孩子的指针RBTreeNode<K, V>* _right;//指向右孩子的指针RBTreeNode<K, V>* _parent;//指向父亲的指针Color _col;//颜色RBTreeNode(const pair<K, V>& kv)//节点构造:_kv(kv), _left(nullptr), _right(nullptr), _parent(nullptr), _col(RED){}
};//红黑树类
template<class K, class V>
class RBTree
{typedef RBTreeNode<K, V> Node;
public://强制生成无参构造RBTree() = default;//拷贝构造RBTree(const RBTree<K, V>& t){_root = _Copy(t._root);}//析构函数~RBTree(){_Destroy(_root);}//插入bool Insert(const pair<K, V>& kv){if (_root == nullptr)//树为空,直接插入{_root = new Node(kv);_root->_col = BLACK;return true;}//先查找合适的插入位置Node* parent = nullptr;Node* cur = _root;while (cur){if (kv.first < cur->_kv.first){parent = cur;cur = cur->_left;}else if (kv.first > cur->_kv.first){parent = cur;cur = cur->_right;}else{return false;}}cur = new Node(kv);if (kv.first < parent->_kv.first){parent->_left = cur;}else{parent->_right = cur;}cur->_parent = parent;//parent为红,进行平衡调整while (parent && parent->_col == RED){//确定grandfatherNode* grandfather = parent->_parent;if (parent == grandfather->_left){//确定uncleNode* uncle = grandfather->_right;if (uncle && uncle->_col == RED)//uncle为红,仅变色{parent->_col = uncle->_col = BLACK;grandfather->_col = RED;//继续向上判断cur = grandfather;parent = cur->_parent;}else//uncle为黑或不存在,旋转+变色{if (cur == parent->_left)//右单旋{RotateR(grandfather);//变色parent->_col = BLACK;grandfather->_col = RED;}else//左右双旋{RotateL(parent);RotateR(grandfather);//变色cur->_col = BLACK;grandfather->_col = RED;}break;//旋转完成,直接跳出循环}}else{//确定uncleNode* uncle = grandfather->_left;if (uncle && uncle->_col == RED)//uncle为红,仅变色{parent->_col = uncle->_col = BLACK;grandfather->_col = RED;//继续向上判断cur = grandfather;parent = cur->_parent;}else//uncle为黑或不存在,旋转+变色{if (cur == parent->_right)//左单旋{RotateL(grandfather);//变色parent->_col = BLACK;grandfather->_col = RED;}else//右左双旋{RotateR(parent);RotateL(grandfather);//变色cur->_col = BLACK;grandfather->_col = RED;}break;//旋转完成,直接跳出循环}}}//最后将根节点设置为黑色_root->_col = BLACK;return true;}//查找Node* Find(const K& key){Node* cur = _root;while (cur){if (key < cur->_kv.first){cur = cur->_left;//小了往左走}else if (key > cur->_kv.first){cur = cur->_right;//大了往右走}else{return cur;//找到了,返回}}return nullptr;//没找到,返回空指针}//中序遍历void Inorder(){_Inorder(_root);}//判断是否为合法红黑树bool IsValidRBTree(){//空树,合法if (_root == nullptr) return true;//根节点为红,非法if (_root->_col == RED){cout << "根节点为红" << endl;return false;}int refNum = 0;//记录黑色节点个数Node* cur = _root;while (cur){if (cur->_col == BLACK) refNum++;cur = cur->_left;}//递归检查所有路径return _Check(_root, 0, refNum);}
private://右单旋void RotateR(Node* parent){Node* subL = parent->_left;Node* subLR = subL->_right;parent->_left = subLR;if (subLR) subLR->_parent = parent;Node* ppNode = parent->_parent;subL->_right = parent;parent->_parent = subL;if (parent == _root){_root = subL;subL->_parent = nullptr;}else{if (ppNode->_left == parent) ppNode->_left = subL;else ppNode->_right = subL;subL->_parent = ppNode;}}//左单旋void RotateL(Node* parent){Node* subR = parent->_right;Node* subRL = subR->_left;parent->_right = subRL;if (subRL) subRL->_parent = parent;Node* ppNode = parent->_parent;subR->_left = parent;parent->_parent = subR;if (parent == _root){_root = subR;subR->_parent = nullptr;}else{if (ppNode->_left == parent) ppNode->_left = subR;else ppNode->_right = subR;subR->_parent = ppNode;}}//中序遍历void _Inorder(Node* root){if (root == nullptr) return;_Inorder(root->_left);cout << root->_kv.first << ' ' << root->_kv.second << endl;_Inorder(root->_right);}//拷贝构造Node* _Copy(Node* root, Node* parent = nullptr){if (root == nullptr) return nullptr;Node* NewRoot = new Node(root->_kv);NewRoot->_col = root->_col;//复制颜色NewRoot->_parent = parent;//设置父指针//递归拷贝左子树和右子树NewRoot->_left = _Copy(root->_left, NewRoot);NewRoot->_right = _Copy(root->_right, NewRoot);return NewRoot;}//销毁void _Destroy(Node* root){if (root == nullptr) return;_Destroy(root->_left);_Destroy(root->_right);delete root;}//路径检查bool _Check(Node* root, int num, const int refNum){if (root == nullptr){//遍历到空,进行黑色节点比较if (num != refNum){cout << "黑色节点数量不相等" << endl;return false;}return true;}//检查是否有连续红色节点if (root->_col == RED && root->_parent->_col == RED){cout << "有连续红色节点" << endl;return false;}//记录当前路径的黑色节点数if (root->_col == BLACK) num++;//递归检查左子树和右子树return _Check(root->_left, num, refNum) && _Check(root->_right, num, refNum);}Node* _root = nullptr;//根节点指针
};int main()
{RBTree<int, int> t;int a[] = { 4, 2, 6, 1, 3, 5, 15, 7, 16, 14 };for (auto& e : a){t.Insert({ e,e });}t.Inorder();cout << t.IsValidRBTree() << endl;return 0;
}总结
红黑树通过引入节点颜色和一系列平衡规则,在保持高效查询性能的同时,优化了插入和删除操作的复杂度。与AVL树相比,红黑树对平衡的要求较为宽松,避免了频繁的旋转调整,从而提升了动态操作的效率。尽管红黑树的结构较为复杂,但它通过颜色标记、旋转操作以及路径黑色节点数量的控制,成功实现了查找、插入和删除操作的平衡。在实际应用中,红黑树被广泛用于操作系统、数据库等领域,发挥着其重要的作用。如果你觉得博主讲的还不错,就请留下一个小小的赞在走哦,感谢大家的支持❤❤❤
相关文章:

【数据结构进阶】红黑树超详解 + 实现(附源码)
🌟🌟作者主页:ephemerals__ 🌟🌟所属专栏:数据结构 目录 前言 一、红黑树介绍 二、红黑树原理详解 三、红黑树的实现 1. 节点定义 2. 红黑树类型定义及接口声明 3. 红黑树的插入(重点&a…...

leetcode_3092. 最高频率的 ID
https://leetcode.cn/problems/most-frequent-ids/description/ 看到这个数据范围 最极端情况 如果nums全为一个数 并且数量取到最大 那么范围是10的10次方 需要longlong储存 这题主要运用了哈希表配合multiset实现 哈希表主要用作存储某个数的出现次数 mst则用于记录出现次…...

鸿蒙仓颉环境配置(仓颉SDK下载,仓颉VsCode开发环境配置,仓颉DevEco开发环境配置)
目录 1)仓颉的SDK下载 1--进入仓颉的官网 2--点击图片中的下载按钮 3--在新跳转的页面点击即刻下载 4--下载 5--找到你们自己下载好的地方 6--解压软件 2)仓颉编程环境配置 1--找到自己的根目录 2--进入命令行窗口 3--输入 envsetup.bat 4--验证是否安…...

数据统计–图形报表(day11)
Apache ECharts 介绍 Apache ECharts 介绍 Apache ECharts 是一款基于 Javascript 的数据可视化图表库,提供直观,生动,可交互,可个性化定制的数据可视化图表。 官网地址:Apache ECharts 入门案例 Apache Echarts官方…...

源码分析之Openlayers样式篇CircleStyle类
访问Openlayers网站(https://jinuss.github.io/Openlayers_map_pages/,网站是基于Vue3 Openlayers,里面有大量的实践和案例。觉得还不错,可以 给个小星星Star,鼓励一波 https://github.com/Jinuss/OpenlayersMap哦~ 概述 在 Ope…...

解决CentOS9系统下Zabbix 7.2图形中文字符乱码问题
操作系统:CentOS 9 Zabbix版本:Zabbix7.2 问题描述:主机图形中文字符乱码 解决方案: # 安装字体配置和中文语言包 sudo yum install -y fontconfig langpacks-zh_CN.noarch # 检查是否已有中文字体: fc-list :lan…...

AF3 FourierEmbedding类源码解读
FourierEmbedding 是一个用于扩散条件的傅里叶嵌入类,其核心是将输入的时间步噪声强度或控制参数(timestep)转换为高维的周期性特征。 源代码: class FourierEmbedding(nn.Module):"""Fourier embedding for diffusion conditioning."""de…...

vsftpd虚拟用户部署
vsftpd虚拟用户部署 案例提供两个用户如下,使用centos7验证可行。 test *AO9ih&7 ftp DTx4zp_shell脚本运行一键安装vsftp #!/bin/bash yum -y install vsftpd ftp >/etc/vsftpd/vsftpd.conf cat <<EOL >> /etc/vsftpd/vsftpd.conf anonymous_enableNO l…...

MySQL 容器已经停止(但仍然存在),但希望重新启动它,并使它的 3306 端口映射到宿主机的 3306 端口是不可行的
重新启动容器并映射端口是不行的 由于你已经有一个名为 mysql-container 的 MySQL 容器,你可以使用 docker start 启动它。想要让3306 端口映射到宿主机是不行的,实际上,端口映射是在容器启动时指定的。你无法在容器已经创建的情况下直接修改…...

汇编实验·顺序程序设计
一、实验目的: 1.能够熟练的进行顺序程序的编写,掌握基本的汇编语言指令的用法 2.通过程序设计理解掌握不同类型的数据混合运算的基本规则 3.熟练掌握各种寻址方式,深入理解逻辑地址和物理地址的相关概念 二、实验内容 有三个长度分别为1、2、4个字节的数据,编写程序求…...

AIGC视频扩散模型新星:Video 版本的SD模型
大家好,这里是好评笔记,公主号:Goodnote,专栏文章私信限时Free。本文详细介绍慕尼黑大学携手 NVIDIA 等共同推出视频生成模型 Video LDMs。NVIDIA 在 AI 领域的卓越成就家喻户晓,而慕尼黑大学同样不容小觑,…...

HarmonyOS:通过(SQLite)关系型数据库实现数据持久化
一、场景介绍 关系型数据库基于SQLite组件,适用于存储包含复杂关系数据的场景,比如一个班级的学生信息,需要包括姓名、学号、各科成绩等,又或者公司的雇员信息,需要包括姓名、工号、职位等,由于数据之间有较…...

10. SpringCloud Alibaba Sentinel 规则持久化部署详细剖析
10. SpringCloud Alibaba Sentinel 规则持久化部署详细剖析 文章目录 10. SpringCloud Alibaba Sentinel 规则持久化部署详细剖析1. 规则持久化1.1 Nacos Server 配置中心-规则持久化实例 2. 最后: 1. 规则持久化 规则没有持久化的问题 如果 sentinel 流控规则没有…...

STM32更新程序OTA
STM32的OTA(Over-The-Air)更新程序是一种通过无线通信方式,为设备分发新软件、配置甚至更新加密密钥的技术。以下是关于STM32 OTA更新程序的详细介绍: 一、OTA升级流程 STM32的OTA升级流程通常包括以下几个关键步骤:…...
|稀土掘金-147.寻找独一无二的糖葫芦串、119.游戏队友搜索)
MarsCode青训营打卡Day10(2025年1月23日)|稀土掘金-147.寻找独一无二的糖葫芦串、119.游戏队友搜索
资源引用: 147.寻找独一无二的糖葫芦串 119.游戏队友搜索 今日小记: 回乡聚会陪家人,休息一天~ 稀土掘金-147.寻找独一无二的糖葫芦串(147.寻找独一无二的糖葫芦串) 题目分析: 给定n个长度为m的字符串表…...
 : 安装组件出错解决)
vue(33) : 安装组件出错解决
1. request to https://registry.npm.taobao.org/semver/download/semver-6.1.1.tgz?cache0&other_urlshttps%3A%2F%2Fregistry.npm.taobao.org%2Fsemver%2Fdownload%2Fsemver-6.1.1.tgz failed, reason: certificate has expired 这个错误提示表明你在尝试从https://reg…...

ChatGPT结合Excel辅助学术数据分析详细步骤分享!
目录 一.Excel在学术论文中的作用✔ 二.Excel的提示词✔ 三. 编写 Excel 命令 四. 编写宏 五. 执行复杂的任务 六. 将 ChatGPT 变成有用的 Excel 助手 一.Excel在学术论文中的作用✔ Excel作为一种广泛使用的电子表格软件,在学术论文中可以发挥多种重要作用&a…...
stm32f103 单片机(一)第一个工程
先看一个简单的 系统上已经安装好了keil5 与ARM包,也下载好了STM32固件库 新建一个工程,添加三个组 加入如下文件 在options 里作如下配置 准备在main.c 中写下第一个实验,点亮一个小灯。 像51单片机一样直接对引脚赋值是行不通的 在…...
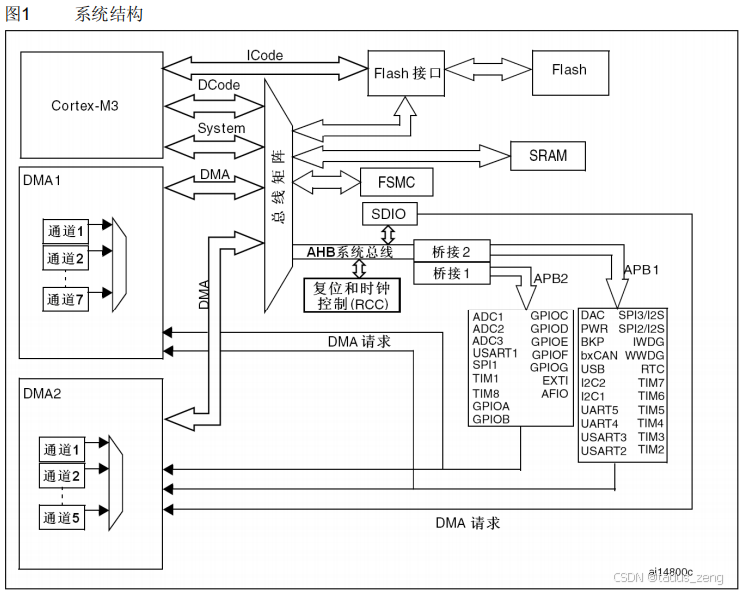
云计算和服务器
一、云计算概述 ICT是世界电信协会在2001年的全球性会议上提出的综合性概念,ICT分为IT和CT,IT(information technology)信息技术,负责对数据生命周期的管理;CT(communication technology),负责数据的传输管理。 CT技术…...
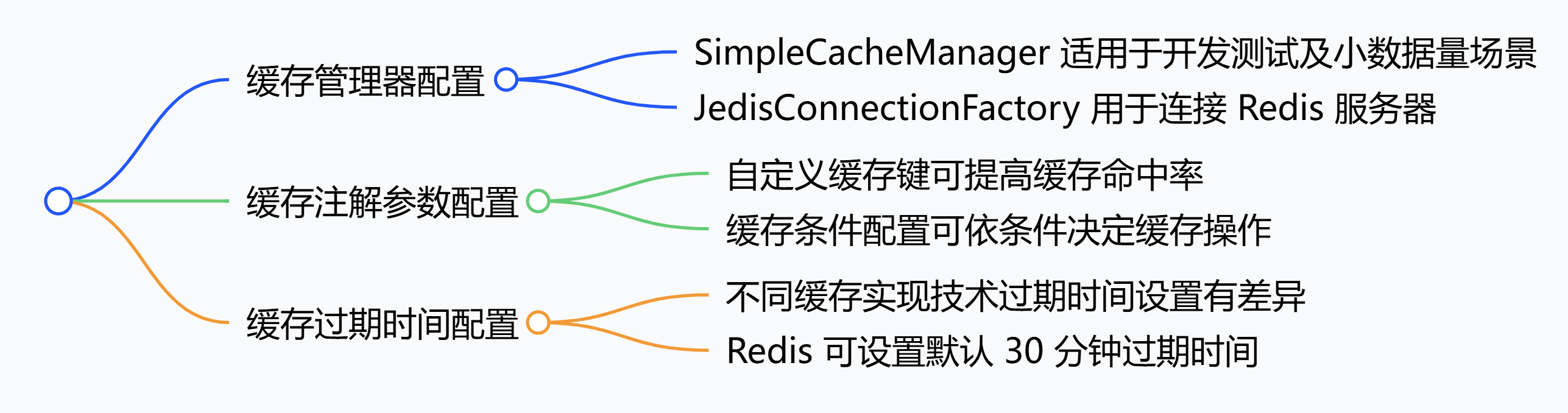
Spring 框架:配置缓存管理器、注解参数与过期时间
在 Spring 框架中,可通过多种方式配置缓存具体行为,常见配置方法如下。 1. 缓存管理器(CacheManager)配置 基于内存的缓存管理器配置(以SimpleCacheManager为例) SimpleCacheManager 是 Spring 提供的简单…...

渗透实战PortSwigger靶场-XSS Lab 14:大多数标签和属性被阻止
<script>标签被拦截 我们需要把全部可用的 tag 和 event 进行暴力破解 XSS cheat sheet: https://portswigger.net/web-security/cross-site-scripting/cheat-sheet 通过爆破发现body可以用 再把全部 events 放进去爆破 这些 event 全部可用 <body onres…...

力扣热题100 k个一组反转链表题解
题目: 代码: func reverseKGroup(head *ListNode, k int) *ListNode {cur : headfor i : 0; i < k; i {if cur nil {return head}cur cur.Next}newHead : reverse(head, cur)head.Next reverseKGroup(cur, k)return newHead }func reverse(start, end *ListNode) *ListN…...

【threejs】每天一个小案例讲解:创建基本的3D场景
代码仓 GitHub - TiffanyHoo/three_practices: Learning three.js together! 可自行clone,无需安装依赖,直接liver-server运行/直接打开chapter01中的html文件 运行效果图 知识要点 核心三要素 场景(Scene) 使用 THREE.Scene(…...
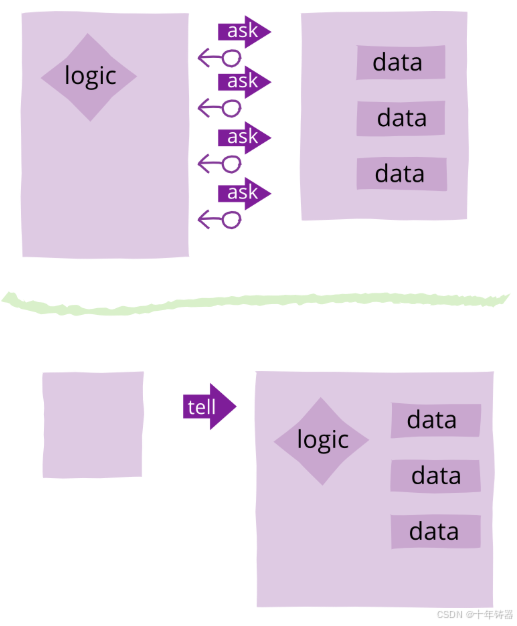
ABAP设计模式之---“Tell, Don’t Ask原则”
“Tell, Don’t Ask”是一种重要的面向对象编程设计原则,它强调的是对象之间如何有效地交流和协作。 1. 什么是 Tell, Don’t Ask 原则? 这个原则的核心思想是: “告诉一个对象该做什么,而不是询问一个对象的状态再对它作出决策。…...

视觉slam--框架
视觉里程计的框架 传感器 VO--front end VO的缺点 后端--back end 后端对什么数据进行优化 利用什么数据进行优化的 后端是怎么进行优化的 回环检测 建图 建图是指构建地图的过程。 构建的地图是点云地图还是什么信息的地图? 建图并没有一个固定的形式和算法…...

统计按位或能得到最大值的子集数目
我们先来看题目描述: 给你一个整数数组 nums ,请你找出 nums 子集 按位或 可能得到的 最大值 ,并返回按位或能得到最大值的 不同非空子集的数目 。 如果数组 a 可以由数组 b 删除一些元素(或不删除)得到,…...

开源项目实战学习之YOLO11:12.6 ultralytics-models-tiny_encoder.py
👉 欢迎关注,了解更多精彩内容 👉 欢迎关注,了解更多精彩内容 👉 欢迎关注,了解更多精彩内容 ultralytics-models-sam 1.sam-modules-tiny_encoder.py2.数据处理流程3.代码架构图(类层次与依赖)blocks.py: 定义模型中的各种模块结构 ,如卷积块、残差块等基础构建…...

【Ragflow】27.RagflowPlus(v0.4.1):小版本迭代,问题修复与功能优化
概述 RagflowPlus v0.4.0 在发布后,收到了积极的反馈,同时也包含一些问题。 本次进行一轮小版本更新,发布 v0.4.1 版本,对已知问题进行修复,并对部分功能进行进一步优化。 开源地址:https://github.com/…...

STM32+MPU6050传感器
#创作灵感## 在嵌入式系统开发中,STM32F103C8T6单片机与MPU6050传感器的组合因其高性能、低功耗以及丰富的功能而备受青睐。本文将简单介绍如何在Keil 5开发环境中实现STM32F103C8T6与MPU6050的连接和基本数据采集,带你快速入门智能硬件开发。 一、硬件…...

【原理解析】为什么显示器Fliker dB值越大,闪烁程度越轻?
显示器Fliker 1 显示器闪烁现象说明2 Fliker量测方法2.1 FMA法2.2 JEITA法问题答疑:为什么显示器Fliker dB值越大,闪烁程度越轻? 3 参考文献 1 显示器闪烁现象说明 当一个光源闪烁超过每秒10次以上就可在人眼中产生视觉残留,此时…...

