一、引论,《组合数学(第4版)》卢开澄 卢华明
零、前言
发现自己数数题做的很烂,重新学一遍组合数学吧。
参考卢开澄 卢华明 编著的《组合数学(第4版)》,只打算学前四章。
通过几个经典问题来了解组合数学所研究的内容。
一、幻方问题
据说大禹治水之前,河里冒出来一只乌龟,龟背上是一个3*3的矩阵,每个格子里面有若干点,行和列和对角线和都相等且为15。然后大禹就以15为周期来治水了。
对于一个nxn的矩阵,满足行和,列和,主副对角线和都相等,那么这个矩阵就是一个n阶幻方。
最早研究幻方的是南宋的杨辉(杨辉三角那个),他罗列了3x3、4x4、5x5甚至10x10的幻方。
定义:行/列整数和为该幻方的幻和。
n 阶幻方的幻和为 (n^2 + 1) * n / 2
并非任意阶幻方都有解法:
2阶幻方就不存在:

会推出某两个元素相等,但是a b c d 互不相同。
大约30年前,德国数学家L · Bieberbach证明:
对于任意大于等于 3 的数 n,都存在一个 n 阶的幻方阵。
杨辉提出了一种三阶幻方的构造方法:
- 123、456、789 斜着摆三列,得到一个菱形
- 交换菱形对角元素,挤压成一个正方形,就是一个三阶幻方
但是对于更高阶该如何构造呢?
法国一位数学家研究了奇数阶幻方的一般化构造方法:
- 记第 i 行 第 j 列 方格坐标为 (i, j),0 索引
- 初始将 1 放在第 0 行的中间 (0, n / 2)
- 对于 当前要放置的棋子,上一枚棋子的坐标为 (x, y)
- 我们尝试放在 ((x - 1) % n, (y + 1 % n))
- 如果已经被占用,则放在 ((x + 1) % n, y)
- 证明略
事实上,我们可以将幻方分成三类:
- 奇数阶幻方
- 4m 阶幻方
- 4m + 2 阶幻方
每一类都有对应的构造算法。
然而我们发现杨辉构造的三阶幻方和奇数阶构造算法得到的幻方不同,但是把幻方上下翻转就相同了。

这让我们思考,对于n阶幻方有多少种构造方法?
三阶幻方,如果认为翻转旋转一样的话,只有一种。
四阶幻方,如果认为翻转旋转一样的话,有880种,否则有7040.
五阶已经有 2亿七千多万个了。
六阶数学家大概确定了其数量落在某个范围,七阶已经无从得知了……
可见,计数问题是组合数学中的一大难题。
算竞中经常遇到这样一类构造题:行列乘积、gcd、异或等限制来构造矩阵,这其实都是幻方的变形。
二、羊皮纸卷
阿基米德在羊皮纸上的论文流落到寺庙,僧人清洗后重新抄写经文。
2003年,科学家通过X光照射,发现羊皮纸经文下面的阿基米德关于十四巧板的论文。

一位数学家以此为题,设置100美元奖项,谁先解出来给谁。
然后计算机学家借助计算机设计算法解出来是17152种,后来数学家利用排列组合的方式,也得到了正解。阿基米德无意间开创了西方世界的组合数学的篇章。
1666年,莱布尼茨研究概率学时,生造了**组合数学(Combinatorics)**这个单词。
三、手机密码安全吗
平时在学校基本都是翘课,有一次遇到学习通4位密码签到,我一看乐了,整个程序暴力枚举,几乎一瞬间就签上到了。
为什么这么快呢?
4位密码,每位10种可能,也就10000种,计算机基本几毫秒就能枚举完所有可能。
很多人手机都有3 * 3 的手势密码,其实手势密码可以看作是从一个格子出发得到的一条路径,我们怎么计数呢?
正难则反,总情况 - 不合法路径。
不合法的定义:如果选择的两个点连成的线段,穿越了第三个点,如果这第三个点,之前没有被连过,则不合法;反之,则合法
通过计算机程序得到一共有 389112 种方案。
可见,如果手机没有输入次数限制的话,一部手机很快就能被破解。
计数问题是一类很常见的问题,但是并不简单,如何做到不重不漏,是一个难点。
四、世界杯引出的问题
n 支球队参加比赛,一共需要多少场复赛?
比较笨的方法:局面抽象成节点,代表当前剩下的队伍集合,挑出两个队伍比赛,扔掉一个败者,得到新的节点,最后节点的数目就是总比赛场数。
但事实上,每进行一场比赛都会产生一个败者,一个胜者,我们最后只有一个冠军,所以要进行n - 1场比赛。
可见同样是计数问题,不同方法的效率是天差地别的。
五、哥尼斯堡七桥问题
即欧拉路径问题:欧拉图,欧拉通路,欧拉回路,Hierholzer算法详解-CSDN博客
沿着桥走,每个桥恰好走一次有多少种走法?
我们能直接取排列数作为答案吗?
显然不能,太多非法解了。
不过我们可以借助定理 + 计算机枚举来求解。
通过定理,我们保证枚举方案的合法性,可见有技巧的枚举可以更加精巧简洁。
相关文章:

一、引论,《组合数学(第4版)》卢开澄 卢华明
零、前言 发现自己数数题做的很烂,重新学一遍组合数学吧。 参考卢开澄 卢华明 编著的《组合数学(第4版)》,只打算学前四章。 通过几个经典问题来了解组合数学所研究的内容。 一、幻方问题 据说大禹治水之前,河里冒出来一只乌龟,…...

Vue3+TS 实现批量拖拽文件夹上传图片组件封装
1、html 代码: 代码中的表格引入了 vxe-table 插件 <Tag /> 是自己封装的说明组件 表格列表这块我使用了插槽来增加扩展性,可根据自己需求,在组件外部做调整 <template><div class"dragUpload"><el-dialo…...
)
二叉树的所有路径(力扣257)
因为题目要求路径是从上到下的,所以最好采用前序遍历。这样可以保证按从上到下的顺序将节点的值存入一个路径数组中。另外,此题还有一个难点就是如何求得所有路径。为了解决这个问题,我们需要用到回溯。回溯和递归不分家,每递归一…...
缓存)
Python OrderedDict 实现 Least Recently used(LRU)缓存
OrderedDict 实现 Least Recently used(LRU)缓存 引言正文 引言 LRU 缓存是一种缓存替换策略,当缓存空间不足时,会移除最久未使用的数据以腾出空间存放新的数据。LRU 缓存的特点: 有限容量:缓存拥有固定的…...

LabVIEW项目中的工控机与普通电脑选择
工控机(Industrial PC)与普通电脑在硬件设计、性能要求、稳定性、环境适应性等方面存在显著差异。了解这些区别对于在LabVIEW项目中选择合适的硬件至关重要。下面将详细分析这两种设备的主要差异,并为LabVIEW项目中的选择提供指导。 硬件设…...

Ansys Speos | Speos Meshing 网格最佳实践
概述 网格划分是在各种计算应用中处理3D几何的基本步骤: 表面和体积:网格允许通过将复杂的表面和体积分解成更简单的几何元素(如三角形、四边形、四面体或六面体)来表示复杂的表面和体积。 模拟和渲染:网格是创建离散…...

elasticsearch segment数量对读写性能的影响
index.merge.policy.segments_per_tier 是一个配置选项,用于控制 Elasticsearch 中段(segment)合并策略的行为。它定义了在每一层的段合并过程中,允许存在的最大段数量。调整这个参数可以优化索引性能和资源使用。 假设你有一个索…...

全同态加密理论、生态现状与未来展望(中2)
《全同态加密理论、生态现状与未来展望》系列由lynndell2010gmail.com和mutourend2010gmail.com整理原创发布,分为上中下三个系列: 全同态加密理论、生态现状与未来展望(上):专注于介绍全同态加密理论知识。全同态加密…...
鸿蒙UI(ArkUI-方舟UI框架)-开发布局
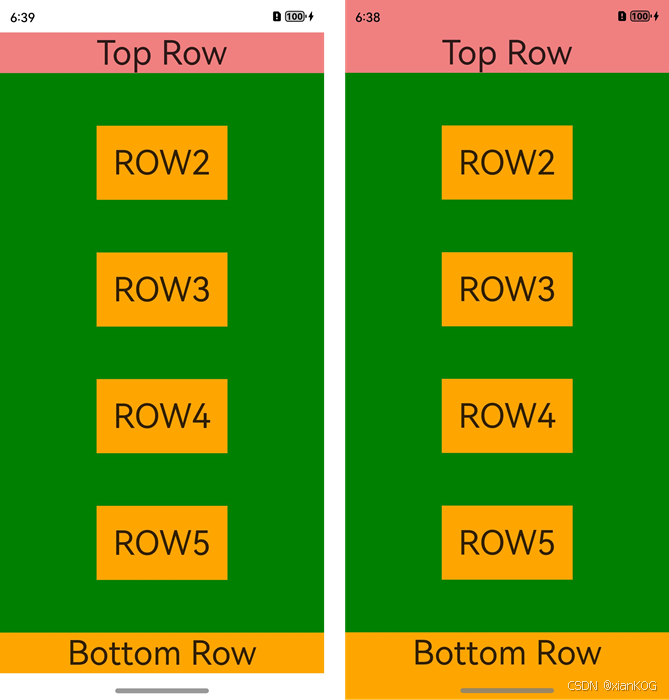
返回主章节 → 鸿蒙UI(ArkUI-方舟UI框架) 开发布局 1、布局概述 1)布局结构 2)布局元素组成 3)如何选择布局 声明式UI提供了以下10种常见布局,开发者可根据实际应用场景选择合适的布局进行页面开发。 …...
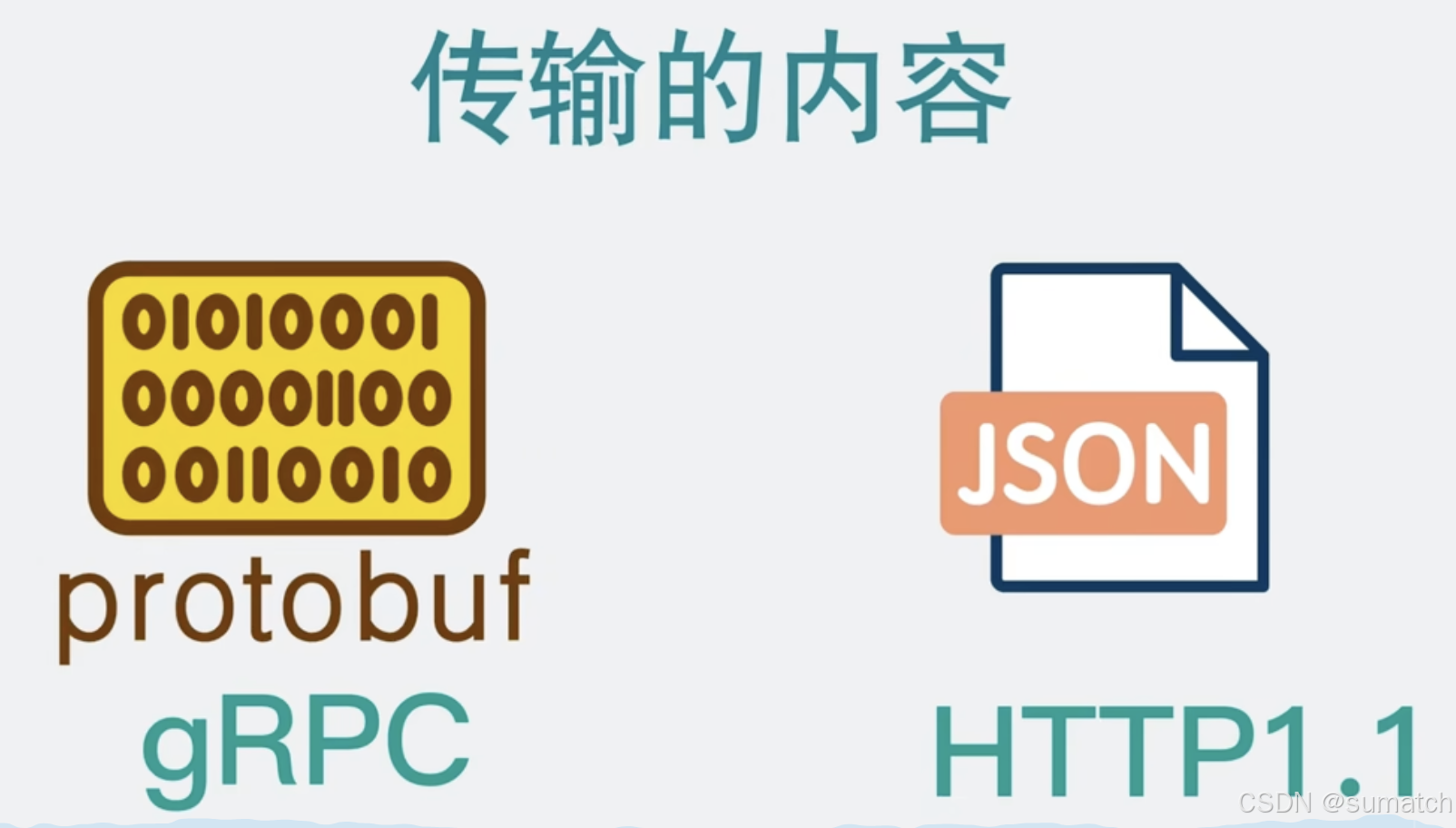
RPC是什么?和HTTP区别?
RPC 是什么?HTTP 是什么? 作为一个程序员,假设我们需要从A电脑的进程发送一段数据到B电脑的进程,我们一般会在代码中使用 Socket 进行编程。 此时,可选性一般就是 TCP 和 UDP 二选一,由于 TCP 可靠、UDP 不…...

Linux C\C++编程-建立文件和内存映射
【图书推荐】《Linux C与C一线开发实践(第2版)》_linux c与c一线开发实践pdf-CSDN博客 《Linux C与C一线开发实践(第2版)(Linux技术丛书)》(朱文伟,李建英)【摘要 书评 试读】- 京东图书 Linu…...
行政纠错——pycorrector学习
pycorrector是一个开源中文文本纠错工具,它支持对中文文本进行音似、形似和语法错误的纠正。此工具是使用Python3进行开发的,并整合了Kenlm、ConvSeq2Seq、BERT、MacBERT、ELECTRA、ERNIE、Transformer等多种模型来实现文本纠错功能。pycorrector官方仓库…...

Go的defer原理
Go 的 defer 原理 defer 是 Go 语言中的一个关键字,用于延迟执行一个函数调用。它通常用于处理资源释放、连接关闭等操作,确保这些操作在函数返回之前执行。 1. 什么是 defer? defer 关键字用于延迟执行一个函数调用,直到包含它…...

Windows 下本地 Docker RAGFlow 部署指南
Windows 下本地 Docker RAGFlow 部署指南 环境要求部署步骤1. 克隆代码仓库2. 配置 Docker 镜像加速(可选)3. 修改端口配置(可选)4. 启动服务5. 验证服务状态6. 访问服务7. 登录系统8. 配置模型8.1 使用 Ollama 本地模型8.2 使用在线 API 服务9. 开始使用10. 常见问题处理端…...

专题三_穷举vs暴搜vs深搜vs回溯vs剪枝_全排列
dfs解决 全排列&子集 1.全排列 link:46. 全排列 - 力扣(LeetCode) 全局变量回溯 code class Solution { public:vector<vector<int>> ans;vector<int> cur;vector<bool> used;vector<vector<int>> permute…...

【IEEE Fellow 主讲报告| EI检索稳定】第五届机器学习与智能系统工程国际学术会议(MLISE 2025)
重要信息 会议时间地点:2025年6月13-15日 中国深圳 会议官网:http://mlise.org EI Compendex/Scopus稳定检索 会议简介 第五届机器学习与智能系统工程国际学术会议将于6月13-15日在中国深圳隆重召开。本次会议旨在搭建一个顶尖的学术交流平台…...

华为E9000刀箱服务器监控指标解读
美信监控易内置了数千种常见设备监测器,能够监测超过20万项指标。这些指标涵盖了从硬件设备到软件系统,从网络性能到安全状态等各个方面。如下基于美信监控易——IT基础监控模块,对华为E9000刀箱服务器部分监控指标进行解读。 一、华为E9000…...

【LC】2544. 交替数字和
题目描述: 给你一个正整数 n 。n 中的每一位数字都会按下述规则分配一个符号: 最高有效位 上的数字分配到 正 号。剩余每位上数字的符号都与其相邻数字相反。 返回所有数字及其对应符号的和。 示例 1: 输入:n 521 输出&…...
QT QTreeWidget控件 全面详解
本系列文章全面的介绍了QT中的57种控件的使用方法以及示例,包括 Button(PushButton、toolButton、radioButton、checkBox、commandLinkButton、buttonBox)、Layouts(verticalLayout、horizontalLayout、gridLayout、formLayout)、Spacers(verticalSpacer、horizontalSpacer)、…...
欧几里得算法求最小公倍数和最大公约数
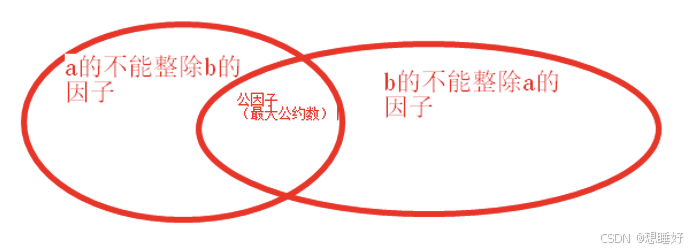
一.最大公约数 gcd(a,b)gcd(b,a%b) 递归式,当且仅当b0,易得0和a的公约数为a.(可作为递归的出口) 证明: int gcd(int a, int b) {if (b 0) return a;else return gcd(b, a % b); } 二.最小公倍数 给定整数a b,求a b的最小公倍数 有图可知…...

TDengine 快速体验(Docker 镜像方式)
简介 TDengine 可以通过安装包、Docker 镜像 及云服务快速体验 TDengine 的功能,本节首先介绍如何通过 Docker 快速体验 TDengine,然后介绍如何在 Docker 环境下体验 TDengine 的写入和查询功能。如果你不熟悉 Docker,请使用 安装包的方式快…...

QMC5883L的驱动
简介 本篇文章的代码已经上传到了github上面,开源代码 作为一个电子罗盘模块,我们可以通过I2C从中获取偏航角yaw,相对于六轴陀螺仪的yaw,qmc5883l几乎不会零飘并且成本较低。 参考资料 QMC5883L磁场传感器驱动 QMC5883L磁力计…...

YSYX学习记录(八)
C语言,练习0: 先创建一个文件夹,我用的是物理机: 安装build-essential 练习1: 我注释掉了 #include <stdio.h> 出现下面错误 在你的文本编辑器中打开ex1文件,随机修改或删除一部分,之后…...

(二)原型模式
原型的功能是将一个已经存在的对象作为源目标,其余对象都是通过这个源目标创建。发挥复制的作用就是原型模式的核心思想。 一、源型模式的定义 原型模式是指第二次创建对象可以通过复制已经存在的原型对象来实现,忽略对象创建过程中的其它细节。 📌 核心特点: 避免重复初…...

从零实现STL哈希容器:unordered_map/unordered_set封装详解
本篇文章是对C学习的STL哈希容器自主实现部分的学习分享 希望也能为你带来些帮助~ 那咱们废话不多说,直接开始吧! 一、源码结构分析 1. SGISTL30实现剖析 // hash_set核心结构 template <class Value, class HashFcn, ...> class hash_set {ty…...

Linux-07 ubuntu 的 chrome 启动不了
文章目录 问题原因解决步骤一、卸载旧版chrome二、重新安装chorme三、启动不了,报错如下四、启动不了,解决如下 总结 问题原因 在应用中可以看到chrome,但是打不开(说明:原来的ubuntu系统出问题了,这个是备用的硬盘&a…...

12.找到字符串中所有字母异位词
🧠 题目解析 题目描述: 给定两个字符串 s 和 p,找出 s 中所有 p 的字母异位词的起始索引。 返回的答案以数组形式表示。 字母异位词定义: 若两个字符串包含的字符种类和出现次数完全相同,顺序无所谓,则互为…...

vue3+vite项目中使用.env文件环境变量方法
vue3vite项目中使用.env文件环境变量方法 .env文件作用命名规则常用的配置项示例使用方法注意事项在vite.config.js文件中读取环境变量方法 .env文件作用 .env 文件用于定义环境变量,这些变量可以在项目中通过 import.meta.env 进行访问。Vite 会自动加载这些环境变…...

学习STC51单片机32(芯片为STC89C52RCRC)OLED显示屏2
每日一言 今天的每一份坚持,都是在为未来积攒底气。 案例:OLED显示一个A 这边观察到一个点,怎么雪花了就是都是乱七八糟的占满了屏幕。。 解释 : 如果代码里信号切换太快(比如 SDA 刚变,SCL 立刻变&#…...
-HIve数据分析)
大数据学习(132)-HIve数据分析
🍋🍋大数据学习🍋🍋 🔥系列专栏: 👑哲学语录: 用力所能及,改变世界。 💖如果觉得博主的文章还不错的话,请点赞👍收藏⭐️留言Ǵ…...
