基于相机内参推导的透视投影矩阵
基于相机内参推导透视投影矩阵(splatam):
M c a m = [ 2 ⋅ f x w 0.0 ( w − 2 ⋅ c x ) w 0.0 0.0 2 ⋅ f y h ( h − 2 ⋅ c y ) h 0.0 0 0 f a r + n e a r n e a r − f a r 2 f a r ⋅ n e a r n e a r − f a r 0.0 0.0 − 1.0 0.0 ] M_{cam}= \begin{bmatrix} \frac{2 \cdot fx}{w} & 0.0 & \frac{(w - 2 \cdot cx)}{w} & 0.0 \\ 0.0 & \frac{2 \cdot fy}{h} & \frac{(h - 2 \cdot cy)}{h} & 0.0 \\ 0 & 0 & \frac{far + near}{near - far} & \frac{2far \cdot near}{near - far} \\ 0.0 & 0.0 & -1.0 & 0.0 \end{bmatrix} Mcam= w2⋅fx0.000.00.0h2⋅fy00.0w(w−2⋅cx)h(h−2⋅cy)near−farfar+near−1.00.00.0near−far2far⋅near0.0
fx: 相机内参中的焦距在x方向上的分量。fy: 相机内参中的焦距在y方向上的分量。cx: 图像中心在x方向上的坐标。cy: 图像中心在y方向上的坐标。w: 图像宽度。h: 图像高度。near: 视锥体(frustum)的近裁剪平面距离。far: 视锥体(frustum)的远裁剪平面距离。
注:此处深度为负
参考透射投影矩阵的数学推导的推导得到透视投影矩阵另一种形式:
M p = [ 2 n r − l 0 r + l r − l 0 0 2 n t − b t + b t − b 0 0 0 f + n n − f 2 f n n − f 0 0 − 1 0 ] M_p = \begin{bmatrix} \frac{2n}{r - l} & 0 & \frac{r + l}{r - l} & 0 \\ 0 & \frac{2n}{t - b} & \frac{t + b}{t - b} & 0 \\ 0 & 0 & \frac{f + n}{n - f} & \frac{2fn}{n - f} \\ 0 & 0 & -1 & 0 \end{bmatrix} Mp= r−l2n0000t−b2n00r−lr+lt−bt+bn−ff+n−100n−f2fn0
n: 近裁剪平面距离。f: 远裁剪平面距离。r: 近裁剪平面的右边界。l: 近裁剪平面的左边界。t: 近裁剪平面的上边界。b: 近裁剪平面的下边界。
可以先看这两个参考再往下看:
参考:
https://zhuanlan.zhihu.com/p/421962223
https://blog.csdn.net/qq_43758883/article/details/116503614
通过视场角来从 M p M_p Mp得到 M c a m M_{cam} Mcam:

上图,忽略y轴,上半部分是相机坐标系,下班部分是像素坐标系,可见相机坐标下的视场角和像素坐标下的视场角是一致的,
1、
在相机坐标系下:
t a n ( f o v x / 2 ) = r − l 2 n tan(fovx/2) = \frac{r-l}{2n} tan(fovx/2)=2nr−l
在像素坐标系下:
t a n ( f o v x / 2 ) = f x w / 2 tan(fovx/2 )= \frac{fx}{w/2} tan(fovx/2)=w/2fx
将上式公式同时提取缩放因子:
t a n ( f o v x / 2 ) = α f α w ′ / 2 = f w ′ / 2 = r − l 2 n tan(fovx/2) = \frac{ \alpha f}{\alpha w'/2} = \frac{ f}{ w'/2} = \frac{r-l}{2n} tan(fovx/2)=αw′/2αf=w′/2f=2nr−l
2、
α ( r − l ) = w α ( r + l ) = ( w − 2 c x ) \begin{align} \alpha (r-l) &= w \\ \alpha (r+l) &= (w - 2cx) \end{align} α(r−l)α(r+l)=w=(w−2cx)
所以,
r + l r − l = ( w − 2 c x ) w \frac {r+l}{r-l} = \frac {(w - 2cx)}{w} r−lr+l=w(w−2cx)
同理,透视投影矩阵y轴也是如此推导。
splatam非标准透视投影
splatam使用的非标准透视投影,与一般不同,splatam是把深度缩放到 [0,1]:
此处深度全取正数,因此第三、四列需要加个负号。
M s p l a t a m = [ 2 ⋅ f x w 0.0 − ( w − 2 ⋅ c x ) w 0.0 0.0 2 ⋅ f y h − ( h − 2 ⋅ c y ) h 0.0 0.0 0.0 f a r f a r − n e a r − ( f a r ⋅ n e a r ) f a r − n e a r 0.0 0.0 1.0 0.0 ] M_{splatam}= \begin{bmatrix} \frac{2 \cdot fx}{w} & 0.0 & \frac{-(w - 2 \cdot cx)}{w} & 0.0 \\ 0.0 & \frac{2 \cdot fy}{h} & \frac{-(h - 2 \cdot cy)}{h} & 0.0 \\ 0.0 & 0.0 & \frac{far}{far - near} & \frac{-(far \cdot near)}{far - near} \\ 0.0 & 0.0 & 1.0 & 0.0 \end{bmatrix} Msplatam= w2⋅fx0.00.00.00.0h2⋅fy0.00.0w−(w−2⋅cx)h−(h−2⋅cy)far−nearfar1.00.00.0far−near−(far⋅near)0.0
可以看到矩阵的第三行与之前的不同,它的作用是把深度最后归一化到 [0,1]。
设相机坐标下的点位置为 [ x c a m , y c a m , z c a m , 1 ] [x_{cam} , y_{cam} ,z_{cam},1] [xcam,ycam,zcam,1],对应裁剪空间坐标为 [ x c , y c , z c , w c ] [x_{c} , y_{c} ,z_{c},w_c] [xc,yc,zc,wc],对应NDC坐标 [ x n , y n , z n , 1 ] [x_{n} , y_{n} ,z_{n},1] [xn,yn,zn,1]。
故:
[ x c y c z c w c ] = M s p l a t a m [ x c a m y c a m z c a m 1 ] \begin{bmatrix}x_{c} \\ y_{c} \\ z_{c} \\w_c \end{bmatrix} =M_{splatam} \begin{bmatrix}x_{cam} \\ y_{cam} \\ z_{cam} \\1 \end{bmatrix} xcyczcwc =Msplatam xcamycamzcam1
考虑深度,即z轴的变换有:
z c = f a r f a r − n e a r z c a m − ( f a r ⋅ n e a r ) f a r − n e a r w c = z c a m \begin{align} z_c &= \frac{far}{far - near} z_{cam} - \frac{(far \cdot near)}{far - near} \\ w_c &= z_{cam} \end{align} zcwc=far−nearfarzcam−far−near(far⋅near)=zcam
归一化处理,得到NDC坐标
z n = z c w c = f a r f a r − n e a r z c a m − ( f a r ⋅ n e a r ) f a r − n e a r z c a m = f a r − ( f a r ⋅ n e a r ) z c a m f a r − n e a r \begin{align} z_n &= \frac {z_c}{w_c} = \frac{\frac{far}{far - near} z_{cam} - \frac{(far \cdot near)}{far - near}}{z_{cam}} \\ &= \frac{far - \frac{(far \cdot near)}{z_{cam}}}{far - near} \end{align} zn=wczc=zcamfar−nearfarzcam−far−near(far⋅near)=far−nearfar−zcam(far⋅near)
故,当 z c a m = n e a r z_{cam} = near zcam=near时, z n = 0 z_n = 0 zn=0, 当 z c a m = f a r z_{cam} = far zcam=far时, z n = 1 z_n = 1 zn=1,所以深度最后是限制在 [0,1]。为什么要怎样设计呢,因为使用3DGS渲染时,只考虑深度大于0的。
相关文章:

基于相机内参推导的透视投影矩阵
基于相机内参推导透视投影矩阵(splatam): M c a m [ 2 ⋅ f x w 0.0 ( w − 2 ⋅ c x ) w 0.0 0.0 2 ⋅ f y h ( h − 2 ⋅ c y ) h 0.0 0 0 f a r n e a r n e a r − f a r 2 f a r ⋅ n e a r n e a r − f a r 0.0 0.0 − 1.0 0.0 ] M_…...

浅析Dubbo 原理:架构、通信与调用流程
一、Dubbo 简介 Dubbo 是阿里巴巴开源的高性能、轻量级的 Java RPC(Remote Procedure Call,远程过程调用)框架,旨在实现不同服务之间的远程通信和调用。在分布式系统中,不同服务可能部署在不同的服务器上,D…...

03垃圾回收篇(D3_垃圾收集器的选择及相关参数)
目录 学习前言 一、收集器的选择 二、GC日志参数 三、垃圾收集相关的常用参数 四、内存分配与回收策略 1. 对象优先在Eden分配 2. 大对象直接进入老年代 3. 长期存活的对象将进入老年代 4. 动态对象年龄判定 5. 空间分配担保 学习前言 本章主要学习垃圾收集器的选择及…...

一、引论,《组合数学(第4版)》卢开澄 卢华明
零、前言 发现自己数数题做的很烂,重新学一遍组合数学吧。 参考卢开澄 卢华明 编著的《组合数学(第4版)》,只打算学前四章。 通过几个经典问题来了解组合数学所研究的内容。 一、幻方问题 据说大禹治水之前,河里冒出来一只乌龟,…...

Vue3+TS 实现批量拖拽文件夹上传图片组件封装
1、html 代码: 代码中的表格引入了 vxe-table 插件 <Tag /> 是自己封装的说明组件 表格列表这块我使用了插槽来增加扩展性,可根据自己需求,在组件外部做调整 <template><div class"dragUpload"><el-dialo…...
)
二叉树的所有路径(力扣257)
因为题目要求路径是从上到下的,所以最好采用前序遍历。这样可以保证按从上到下的顺序将节点的值存入一个路径数组中。另外,此题还有一个难点就是如何求得所有路径。为了解决这个问题,我们需要用到回溯。回溯和递归不分家,每递归一…...
缓存)
Python OrderedDict 实现 Least Recently used(LRU)缓存
OrderedDict 实现 Least Recently used(LRU)缓存 引言正文 引言 LRU 缓存是一种缓存替换策略,当缓存空间不足时,会移除最久未使用的数据以腾出空间存放新的数据。LRU 缓存的特点: 有限容量:缓存拥有固定的…...

LabVIEW项目中的工控机与普通电脑选择
工控机(Industrial PC)与普通电脑在硬件设计、性能要求、稳定性、环境适应性等方面存在显著差异。了解这些区别对于在LabVIEW项目中选择合适的硬件至关重要。下面将详细分析这两种设备的主要差异,并为LabVIEW项目中的选择提供指导。 硬件设…...

Ansys Speos | Speos Meshing 网格最佳实践
概述 网格划分是在各种计算应用中处理3D几何的基本步骤: 表面和体积:网格允许通过将复杂的表面和体积分解成更简单的几何元素(如三角形、四边形、四面体或六面体)来表示复杂的表面和体积。 模拟和渲染:网格是创建离散…...

elasticsearch segment数量对读写性能的影响
index.merge.policy.segments_per_tier 是一个配置选项,用于控制 Elasticsearch 中段(segment)合并策略的行为。它定义了在每一层的段合并过程中,允许存在的最大段数量。调整这个参数可以优化索引性能和资源使用。 假设你有一个索…...

全同态加密理论、生态现状与未来展望(中2)
《全同态加密理论、生态现状与未来展望》系列由lynndell2010gmail.com和mutourend2010gmail.com整理原创发布,分为上中下三个系列: 全同态加密理论、生态现状与未来展望(上):专注于介绍全同态加密理论知识。全同态加密…...
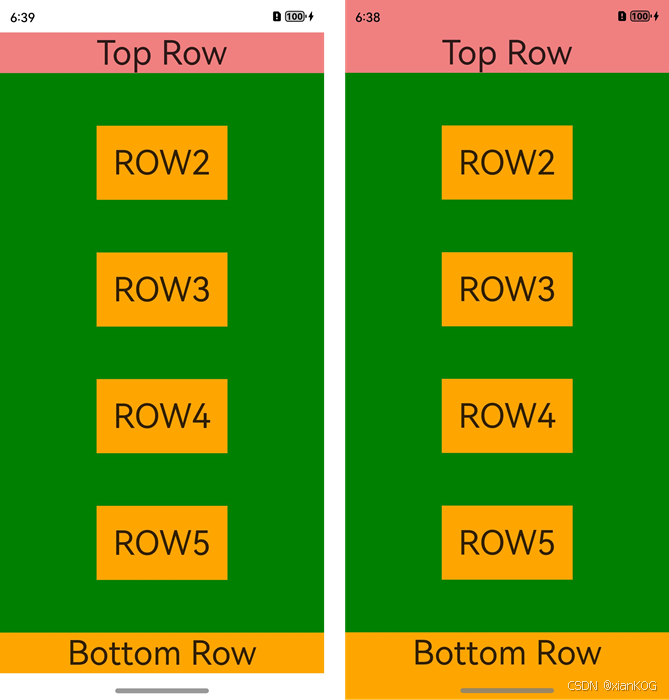
鸿蒙UI(ArkUI-方舟UI框架)-开发布局
返回主章节 → 鸿蒙UI(ArkUI-方舟UI框架) 开发布局 1、布局概述 1)布局结构 2)布局元素组成 3)如何选择布局 声明式UI提供了以下10种常见布局,开发者可根据实际应用场景选择合适的布局进行页面开发。 …...
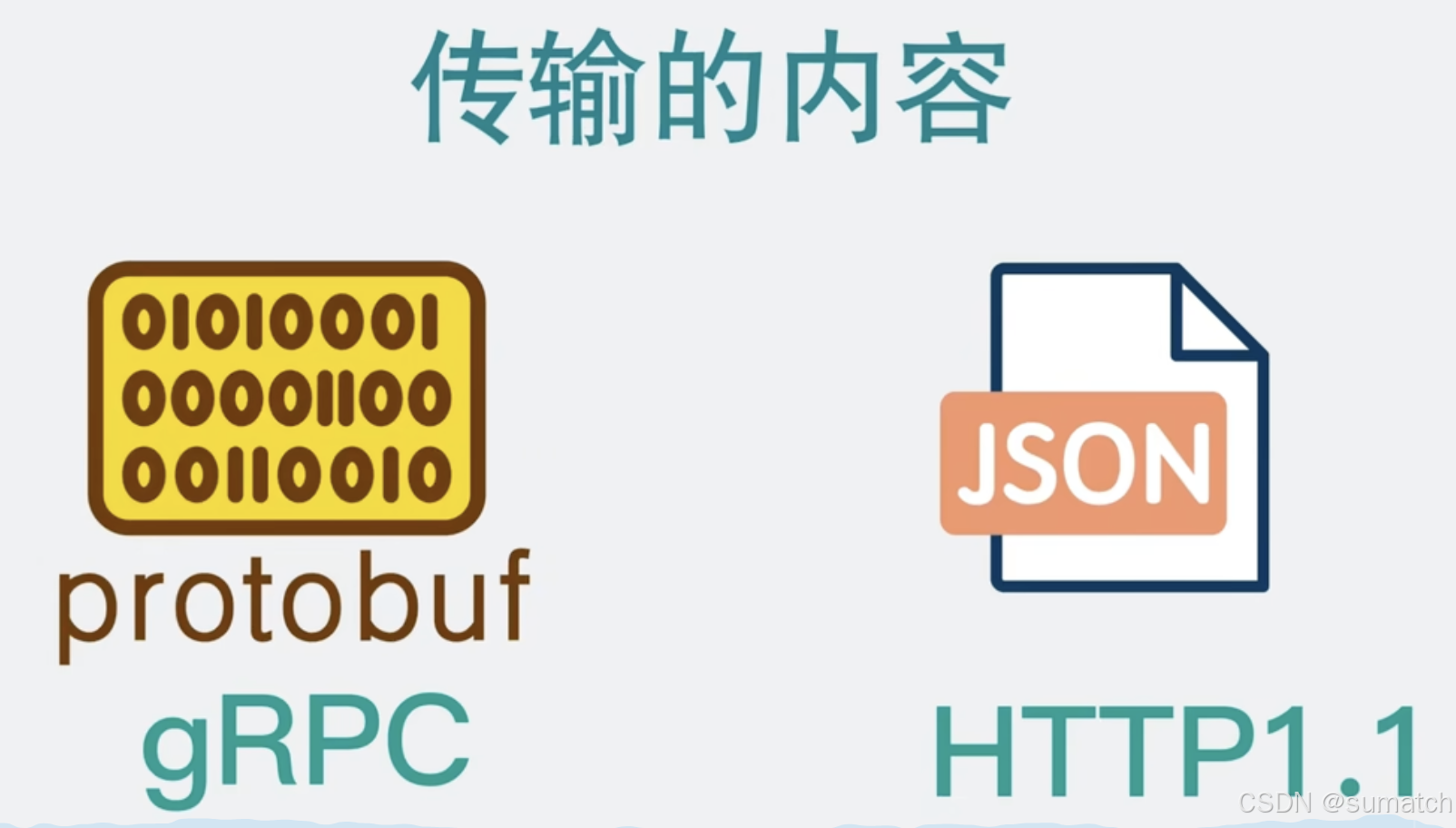
RPC是什么?和HTTP区别?
RPC 是什么?HTTP 是什么? 作为一个程序员,假设我们需要从A电脑的进程发送一段数据到B电脑的进程,我们一般会在代码中使用 Socket 进行编程。 此时,可选性一般就是 TCP 和 UDP 二选一,由于 TCP 可靠、UDP 不…...

Linux C\C++编程-建立文件和内存映射
【图书推荐】《Linux C与C一线开发实践(第2版)》_linux c与c一线开发实践pdf-CSDN博客 《Linux C与C一线开发实践(第2版)(Linux技术丛书)》(朱文伟,李建英)【摘要 书评 试读】- 京东图书 Linu…...
行政纠错——pycorrector学习
pycorrector是一个开源中文文本纠错工具,它支持对中文文本进行音似、形似和语法错误的纠正。此工具是使用Python3进行开发的,并整合了Kenlm、ConvSeq2Seq、BERT、MacBERT、ELECTRA、ERNIE、Transformer等多种模型来实现文本纠错功能。pycorrector官方仓库…...

Go的defer原理
Go 的 defer 原理 defer 是 Go 语言中的一个关键字,用于延迟执行一个函数调用。它通常用于处理资源释放、连接关闭等操作,确保这些操作在函数返回之前执行。 1. 什么是 defer? defer 关键字用于延迟执行一个函数调用,直到包含它…...

Windows 下本地 Docker RAGFlow 部署指南
Windows 下本地 Docker RAGFlow 部署指南 环境要求部署步骤1. 克隆代码仓库2. 配置 Docker 镜像加速(可选)3. 修改端口配置(可选)4. 启动服务5. 验证服务状态6. 访问服务7. 登录系统8. 配置模型8.1 使用 Ollama 本地模型8.2 使用在线 API 服务9. 开始使用10. 常见问题处理端…...

专题三_穷举vs暴搜vs深搜vs回溯vs剪枝_全排列
dfs解决 全排列&子集 1.全排列 link:46. 全排列 - 力扣(LeetCode) 全局变量回溯 code class Solution { public:vector<vector<int>> ans;vector<int> cur;vector<bool> used;vector<vector<int>> permute…...

【IEEE Fellow 主讲报告| EI检索稳定】第五届机器学习与智能系统工程国际学术会议(MLISE 2025)
重要信息 会议时间地点:2025年6月13-15日 中国深圳 会议官网:http://mlise.org EI Compendex/Scopus稳定检索 会议简介 第五届机器学习与智能系统工程国际学术会议将于6月13-15日在中国深圳隆重召开。本次会议旨在搭建一个顶尖的学术交流平台…...

华为E9000刀箱服务器监控指标解读
美信监控易内置了数千种常见设备监测器,能够监测超过20万项指标。这些指标涵盖了从硬件设备到软件系统,从网络性能到安全状态等各个方面。如下基于美信监控易——IT基础监控模块,对华为E9000刀箱服务器部分监控指标进行解读。 一、华为E9000…...

大话软工笔记—需求分析概述
需求分析,就是要对需求调研收集到的资料信息逐个地进行拆分、研究,从大量的不确定“需求”中确定出哪些需求最终要转换为确定的“功能需求”。 需求分析的作用非常重要,后续设计的依据主要来自于需求分析的成果,包括: 项目的目的…...

Java多线程实现之Callable接口深度解析
Java多线程实现之Callable接口深度解析 一、Callable接口概述1.1 接口定义1.2 与Runnable接口的对比1.3 Future接口与FutureTask类 二、Callable接口的基本使用方法2.1 传统方式实现Callable接口2.2 使用Lambda表达式简化Callable实现2.3 使用FutureTask类执行Callable任务 三、…...

HBuilderX安装(uni-app和小程序开发)
下载HBuilderX 访问官方网站:https://www.dcloud.io/hbuilderx.html 根据您的操作系统选择合适版本: Windows版(推荐下载标准版) Windows系统安装步骤 运行安装程序: 双击下载的.exe安装文件 如果出现安全提示&…...

EtherNet/IP转DeviceNet协议网关详解
一,设备主要功能 疆鸿智能JH-DVN-EIP本产品是自主研发的一款EtherNet/IP从站功能的通讯网关。该产品主要功能是连接DeviceNet总线和EtherNet/IP网络,本网关连接到EtherNet/IP总线中做为从站使用,连接到DeviceNet总线中做为从站使用。 在自动…...

多种风格导航菜单 HTML 实现(附源码)
下面我将为您展示 6 种不同风格的导航菜单实现,每种都包含完整 HTML、CSS 和 JavaScript 代码。 1. 简约水平导航栏 <!DOCTYPE html> <html lang"zh-CN"> <head><meta charset"UTF-8"><meta name"viewport&qu…...

dify打造数据可视化图表
一、概述 在日常工作和学习中,我们经常需要和数据打交道。无论是分析报告、项目展示,还是简单的数据洞察,一个清晰直观的图表,往往能胜过千言万语。 一款能让数据可视化变得超级简单的 MCP Server,由蚂蚁集团 AntV 团队…...

Docker 本地安装 mysql 数据库
Docker: Accelerated Container Application Development 下载对应操作系统版本的 docker ;并安装。 基础操作不再赘述。 打开 macOS 终端,开始 docker 安装mysql之旅 第一步 docker search mysql 》〉docker search mysql NAME DE…...

AI+无人机如何守护濒危物种?YOLOv8实现95%精准识别
【导读】 野生动物监测在理解和保护生态系统中发挥着至关重要的作用。然而,传统的野生动物观察方法往往耗时耗力、成本高昂且范围有限。无人机的出现为野生动物监测提供了有前景的替代方案,能够实现大范围覆盖并远程采集数据。尽管具备这些优势…...

并发编程 - go版
1.并发编程基础概念 进程和线程 A. 进程是程序在操作系统中的一次执行过程,系统进行资源分配和调度的一个独立单位。B. 线程是进程的一个执行实体,是CPU调度和分派的基本单位,它是比进程更小的能独立运行的基本单位。C.一个进程可以创建和撤销多个线程;同一个进程中…...

[ACTF2020 新生赛]Include 1(php://filter伪协议)
题目 做法 启动靶机,点进去 点进去 查看URL,有 ?fileflag.php说明存在文件包含,原理是php://filter 协议 当它与包含函数结合时,php://filter流会被当作php文件执行。 用php://filter加编码,能让PHP把文件内容…...
