【第一天】零基础入门刷题Python-算法篇-数据结构与算法的介绍(持续更新)
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档
文章目录
- 前言
- 一、Python数据结构与算法的详细介绍
- 1.基本概念
- 2.Python中的数据结构
- 1. 列表(List)
- 2. 元组(Tuple)
- 3. 字典(Dictionary)
- 4. 集合(Set)
- 5. 字符串(String)
- 3.Python中的常用算法
- 1. 排序算法
- 2. 搜索算法
- 3. 递归算法
- 4. 动态规划
- 5. 贪心算法
- 6. 分治算法
- 7. 回溯算法
- 8. 图论算法
- 9. 字符串算法
- 4.算法的时间复杂度和空间复杂度
- 1. 时间复杂度
- 2. 空间复杂度
- 总结
前言
提示:这里可以添加本文要记录的大概内容:
第一天Python数据结构与算法的详细介绍
第二天五种常见的排序算法
第三天两种常见的搜索算法
第四天两种常见的递归算法
第五天一种常见的动态规划算法
第六天一种常见的贪心算法
提示:以下是本篇文章正文内容,下面案例可供参考
一、Python数据结构与算法的详细介绍
1.基本概念
数据结构:是指计算机中存储和组织数据的方式。不同的数据结构适用于不同的应用场景,选择合适的数据结构可以显著提高程序的运行效率。数据结构涵盖数据内容、数据之间关系和数据操作方法,具有以下设计目标:
- 空间占用尽量少,以节省计算机内存。
- 数据操作尽可能快速,涵盖数据访问、添加、删除、更新等。
- 提供简洁的数据表示和逻辑信息,以便算法高效运行。
算法:是指完成特定任务的一系列步骤或规则,它在有限时间内解决特定问题的一组指令或操作步骤。算法具有以下特性:
- 问题是明确的,包含清晰的输入和输出定义。
- 具有可行性,能够在有限步骤、时间和内存空间下完成。
- 各步骤都有确定的含义,在相同的输入和运行条件下,输出始终相同。
数据结构与算法高度相关、紧密结合,具体表现在以下三个方面:
- 数据结构是算法的基石。数据结构为算法提供了结构化存储的数据,以及操作数据的方法。
- 算法是数据结构发挥作用的舞台。数据结构本身仅存储数据信息,结合算法才能解决特定问题。
- 算法通常可以基于不同的数据结构实现,但执行效率可能相差很大,选择合适的数据结构是关键。
2.Python中的数据结构
Python内置了多种数据结构,涵盖了常见的线性和非线性数据结构。以下是Python中一些主要的数据结构:
1. 列表(List)
- 列表(List):Python中最常用的内置数据结构之一,可以存储任意类型的元素,并且支持动态调整大小。 创建列表:my_list = [](空列表)或my_list = [1, 2, 3, 4, 5](包含元素的列表)。
列表操作:添加元素my_list.append(6)、删除元素my_list.remove(3)、访问元素print(my_list[2])、列表切片print(my_list[1:4])。
2. 元组(Tuple)
- 元组(Tuple):不可变的序列,创建后不能修改。元组通常用于存储固定数量的元素。 创建元组:my_tuple = ()(空元组)或my_tuple = (1, 2, 3, 4, 5)(包含元素的元组)。
元组操作:访问元素print(my_tuple[2])、元组切片print(my_tuple[1:4])。
3. 字典(Dictionary)
- 字典(Dictionary):键值对数据结构,支持快速查找、插入和删除操作。 创建字典:my_dict = {}(空字典)或my_dict = {‘name’: ‘Alice’, ‘age’: 25, ‘city’: ‘New York’}(包含键值对的字典)。
字典操作:添加或更新键值对my_dict[‘age’] = 26、删除键值对del
my_dict[‘city’]、访问值print(my_dict[‘name’])、遍历字典for key, value in
my_dict.items(): print(f’{key}:{value}')。
4. 集合(Set)
- 集合(Set):无序的、不可重复的数据结构,支持集合运算如交集、并集和差集。 创建集合:my_set = set()(空集合)或my_set
= {1, 2, 3, 4, 5}(包含元素的集合)。 集合操作:添加元素my_set.add(6)、删除元素my_set.remove(3)、集合运算(如并集my_set.union(other_set)、交集my_set.intersection(other_set)、差集my_set.difference(other_set))。
5. 字符串(String)
- 字符串(String):有序字符集合,支持多种字符串操作,如拼接、切片、查找等。
此外,Python还支持其他更复杂的数据结构,如栈(Stack)、队列(Queue)、树(Tree)、图(Graph)等。
3.Python中的常用算法
以下是Python中的一些常用算法:
1. 排序算法
- 排序算法:将一组数据按特定顺序排列。常见的排序算法有冒泡排序、选择排序、插入排序、快速排序和归并排序等。
- 冒泡排序:通过重复遍历要排序的数列,比较相邻元素的值,若发现逆序则交换,直到没有逆序为止。时间复杂度为O(n^2),空间复杂度为O(1)。
- 选择排序:每次从未排序部分选择最小(或最大)元素,放到已排序部分的末尾。时间复杂度O(n^2),空间复杂度O(1)。
- 插入排序:将每个新元素插入到已排序部分的适当位置。时间复杂度O(n^2)(最坏情况),空间复杂度O(1)。
- 快速排序:选择一个基准元素,通过一趟排序将待排序的数据分割成独立的两部分,其中一部分的所有数据都比另外一部分的所有数据要小,然后再按此方法对这两部分数据分别进行快速排序,以达到整个数据变成有序序列。时间复杂度为O(n
log n),空间复杂度为O(log n)(递归栈空间)。- 归并排序:采用分治法,将数组分成两半,递归排序后合并。时间复杂度O(n log n),空间复杂度O(n)(需要额外空间合并)。
2. 搜索算法
- 搜索算法:在数据集中查找特定元素。常见的搜索算法有线性搜索和二分搜索等。
- 线性搜索:从数据集的第一个元素开始,依次比较每个元素,直到找到目标元素或搜索完整个数据集为止。时间复杂度为O(n),空间复杂度为O(1)。
- 二分搜索:要求数据集必须是有序的,通过不断将搜索范围减半来查找目标元素。时间复杂度为O(log n),空间复杂度为O(1)。
3. 递归算法
- 递归算法:函数调用自身来解决问题的编程技巧。递归通常用于分治法、树和图的遍历等。
- 斐波那契数列:通过递归调用自身来计算斐波那契数列的第n项。时间复杂度为O(2^n),空间复杂度为O(n)(递归栈空间)。
- 阶乘:通过递归调用自身来计算一个数的阶乘。时间复杂度为O(n),空间复杂度为O(n)(递归栈空间)。
4. 动态规划
- 动态规划:解决最优化问题,通过将问题分解为子问题,并记录子问题的解以避免重复计算。时间复杂度和空间复杂度依具体问题而定,但通常较低于朴素递归解法。
5. 贪心算法
- 贪心算法:在每一步选择中都采取最好或最优(即最有利)的选择,从而希望能够导致结果是全局最好或最优的算法。时间复杂度依具体问题而定。
6. 分治算法
- 分治算法:
将问题划分为几个规模较小的子问题分别解决,然后将子问题的解合并得到原问题的解。快速排序和归并排序是分治算法的典型例子。
7. 回溯算法
- 回溯算法:通过搜索所有可能的候选解来找出所有解的算法。如果候选解被确认不是一个解(或者至少不是最后一个解),回溯算法会通过在上一步进行一些变化来丢弃该解,即“回溯”并尝试另一个可能的候选解。时间复杂度通常很高,因为需要探索所有可能的解空间。
8. 图论算法
- 图论算法:
- 深度优先搜索(DFS):
用途:用于图的遍历或路径查找。
时间复杂度:O(V+E),其中V是顶点数,E是边数。
空间复杂度:O(V)(递归栈空间)。- 广度优先搜索(BFS):
用途:用于图的遍历或最短路径查找(无权图)。
时间复杂度:O(V+E)。
空间复杂度:O(V)(队列空间)。- Dijkstra算法:
用途:用于计算单源最短路径(有权图)。
时间复杂度:O(V^2)(朴素实现)或O((V+E) log V)(优先队列实现)。
空间复杂度:O(V)。
最小生成树算法:- Prim算法:
用途:用于求解最小生成树。
时间复杂度:
使用邻接矩阵:O(V^2)。
使用斐波那契堆等数据结构:O(E log V)。
空间复杂度:根据具体实现而定,通常与顶点数和边的数量相关。- Kruskal算法:
用途:用于求解最小生成树。
时间复杂度:O(E log E),其中E是边的数量。
空间复杂度:O(E)(存储边)和O(V)(并查集数据结构)。- Floyd-Warshall算法:
用途:用于计算所有顶点对之间的最短路径(有权图)。
时间复杂度:O(V^3),其中V是顶点数。注意这里的复杂度是立方,与上述算法不同。
空间复杂度:O(V^2)(存储距离矩阵)。
9. 字符串算法
- 字符串算法:
- KMP算法:用于字符串匹配,时间复杂度O(n+m),其中n和m分别是文本和模式的长度。空间复杂度O(m)。
- Rabin-Karp算法:基于哈希的字符串匹配算法,时间复杂度平均O(n+m),最坏O(n*m)。空间复杂度O(1)(不考虑哈希表)。
4.算法的时间复杂度和空间复杂度
1. 时间复杂度
- 时间复杂度:是指算法运行时间随输入规模增长的变化情况。常见的时间复杂度包括常数时间O(1)、线性时间O(n)、对数时间O(log n)、线性对数时间O(n log n)、平方时间O(n2)、立方时间O(n3)和指数时间O(2^n)等。
2. 空间复杂度
- 空间复杂度:是指算法运行时所需的存储空间随输入规模增长的变化情况。空间复杂度主要衡量算法在运行过程中临时占用存储空间的大小。 在实际应用中,需要根据具体问题的需求和约束条件,选择合适的数据结构和算法,以优化程序的性能。同时,也需要关注算法的时间复杂度和空间复杂度,以确保程序在可接受的范围内运行。
总结
提示:这里对文章进行总结:
例如:以上就是今天要讲的内容,本文简单介绍数据结构与算法的介绍。
相关文章:
)
【第一天】零基础入门刷题Python-算法篇-数据结构与算法的介绍(持续更新)
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言一、Python数据结构与算法的详细介绍1.基本概念2.Python中的数据结构1. 列表(List)2. 元组(Tuple)3. 字典&#…...

租房管理系统实现智能化租赁提升用户体验与运营效率
内容概要 在当今快速发展的租赁市场中,租房管理系统的智能化转型显得尤为重要。它不仅帮助房东和租客之间建立更高效的沟通桥梁,还优化了整个租赁流程。通过智能化技术,这套系统能够自动处理资产管理、合同签署、财务管理等所有关键环节。这…...

python3+TensorFlow 2.x(四)反向传播
目录 反向传播算法 反向传播算法基本步骤: 反向中的参数变化 总结 反向传播算法 反向传播算法(Backpropagation)是训练人工神经网络时使用的一个重要算法,它是通过计算梯度并优化神经网络的权重来最小化误差。反向传播算法的核…...

Flutter 使用 flutter_inappwebview 加载 App 本地 HTML 文件
在 Flutter 开发中,加载本地 HTML 文件是一个常见的需求,尤其是在需要展示离线内容或自定义页面时。flutter_inappwebview 是一个功能强大的插件,支持加载本地文件和网络资源。本文将详细介绍如何使用 flutter_inappwebview 加载 App 本地 HT…...
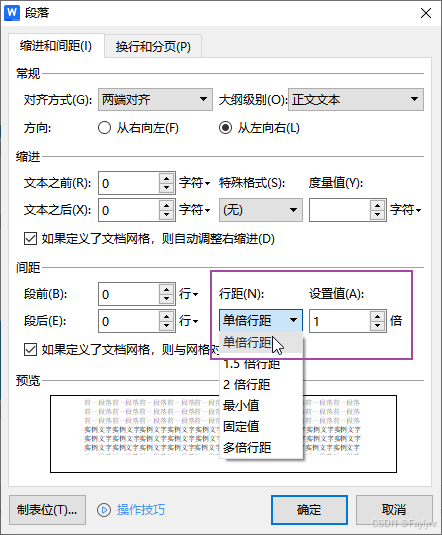
Word常见问题:嵌入图片无法显示完整
场景:在Word中,嵌入式图片显示不全,一部分图片在文字下方。如: 问题原因:因段落行距导致 方法一 快捷方式 选中图片,通过"ctrl1"快捷调整为1倍行距 方法二 通过工具栏调整 选中图片࿰…...

为AI聊天工具添加一个知识系统 之68 详细设计 之9 三种中台和时间度量 之1
本文要点 要点 在维度0上 被分离出来 的业务中台 需求、技术中台要求、和数据中台请求 (分别在时间层/空间层/时空层上 对应一个不同种类槽的容器,分别表示业务特征Feature[3]/技术方面Aspect[3]/数据流Fluent[3]) 在维度1~3的运动过程中 从…...

On to OpenGL and 3D computer graphics
2. On to OpenGL and 3D computer graphics 声明:该代码来自:Computer Graphics Through OpenGL From Theory to Experiments,仅用作学习参考 2.1 First Program Square.cpp完整代码 /// // square.cpp // // OpenGL program to draw a squ…...

从曾国藩的经历看如何打破成长中的瓶颈
《曾国藩传》是一部充满智慧与人生哲理的传记,而曾国藩本人更是一个从“最笨”到“最智慧”的奇人。看他的成长与蜕变,不仅能感受到他如何超越自己的局限,也能从中获得关于人性、社会和历史的重要启示。曾国藩的一生让人深思,正是…...
)
JavaWeb学习-SpringBotWeb开发入门(HTTP协议)
(一)SpringBotWeb开发步骤 (1)创建springboot工程,并勾选开发相关依赖 (2)定义HelloController类,添加方法hello,并添加注解 (3)运行测试 (二)HTTP入门概述 创建请求页面 package com.itheima.demo3; /*请求处理类,加上注解标识为请求处理类*/import org.spr…...

数据库用户管理
数据库用户管理 1.创建用户 MySQL在安装是,会默认创建一个名位root的用户,该用户拥有超级权限,可以控制整个MySQL服务器。 在对MySQL的日常管理和操作中,通常创建一些具有适当权限的用户,尽可能的不用或少用root登录…...

BGP边界网关协议(Border Gateway Protocol)路由聚合详解
一、路由聚合 1、意义 在大规模的网络中,BGP路由表十分庞大,给设备造成了很大的负担,同时使发生路由振荡的几率也大大增加,影响网络的稳定性。 路由聚合是将多条路由合并的机制,它通过只向对等体发送聚合后的路由而…...

ASP.NET Core WebAPI的异步及返回值
目录 Action方法的异步 Action方法参数 捕捉URL占位符 捕捉QueryString的值 JSON报文体 其他方式 Action方法的异步 Action方法既可以同步也可以异步。异步Action方法的名字一般不需要以Async结尾。Web API中Action方法的返回值如果是普通数据类型,那么返回值…...

「 机器人 」仿生扑翼飞行器中的“被动旋转机制”概述
前言 在仿生扑翼飞行器的机翼设计中,模仿昆虫翼的被动旋转机制是一项关键技术。其核心思想在于:机翼旋转角度(攻角)并非完全通过主动伺服来控制,而是利用空气动力和惯性力的作用,自然地实现被动调节。以下对这种设计的背景、原理与优势进行详细说明。 1. 背景:昆虫的被动…...

「 机器人 」扑翼飞行器的数据驱动建模核心方法
前言 数据驱动建模可充分利用扑翼飞行器的已有运行数据,改进动力学模型与控制策略,并对未建模动态做出更精确的预测。在复杂的非线性飞行环境中,该方法能有效弥补传统解析建模的不足,具有较高的研究与应用价值。以下针对主要研究方向和实现步骤进行整理与阐述。 1. 数据驱动…...

个人网站搭建
搭建 LNMP环境搭建: LNMP环境指:Linux Nginx MySQL/MariaDB PHP,在debian上安装整体需要300MB的磁盘空间。MariaDB 是 MySQL 的一个分支,由 MySQL 的原开发者维护,通常在性能和优化上有所改进。由于其轻量化和与M…...

飞书项目流程入门指导手册
飞书项目流程入门指导手册 参考资料准备工作新建空间国际化配置新建工作项字段管理新建字段对接标识授权角色 流程管理基础说明流程节点配置流程节点的布局配置页面上布局按钮布局配置 流程节点驳回流程图展示自动化字段修改 局限性 参考资料 飞书官方参考文档:飞书…...

xss靶场
xss-labs下载地址:GitHub - do0dl3/xss-labs: xss 跨站漏洞平台 xss常见触发标签:XSS跨站脚本攻击实例与防御策略-CSDN博客 level-1 首先查看网页的源代码发现get传参的name的值test插入了html里头,还回显了payload的长度。 <!DOCTYPE …...

XML实体注入漏洞攻与防
JAVA中的XXE攻防 回显型 无回显型 cve-2014-3574...

switch组件的功能与用法
文章目录 1 概念介绍2 使用方法3 示例代码 我们在上一章回中介绍了PageView这个Widget,本章回中将介绍Switch Widget.闲话休提,让我们一起Talk Flutter吧。 1 概念介绍 我们在这里介绍的Switch是指左右滑动的开关,常用来表示某项设置是打开还是关闭。Fl…...

cursor重构谷粒商城05——docker容器化技术快速入门【番外篇】
前言:这个系列将使用最前沿的cursor作为辅助编程工具,来快速开发一些基础的编程项目。目的是为了在真实项目中,帮助初级程序员快速进阶,以最快的速度,效率,快速进阶到中高阶程序员。 本项目将基于谷粒商城…...

AtCoder 第409场初级竞赛 A~E题解
A Conflict 【题目链接】 原题链接:A - Conflict 【考点】 枚举 【题目大意】 找到是否有两人都想要的物品。 【解析】 遍历两端字符串,只有在同时为 o 时输出 Yes 并结束程序,否则输出 No。 【难度】 GESP三级 【代码参考】 #i…...

RNN避坑指南:从数学推导到LSTM/GRU工业级部署实战流程
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文全面剖析RNN核心原理,深入讲解梯度消失/爆炸问题,并通过LSTM/GRU结构实现解决方案,提供时间序列预测和文本生成…...

在QWebEngineView上实现鼠标、触摸等事件捕获的解决方案
这个问题我看其他博主也写了,要么要会员、要么写的乱七八糟。这里我整理一下,把问题说清楚并且给出代码,拿去用就行,照着葫芦画瓢。 问题 在继承QWebEngineView后,重写mousePressEvent或event函数无法捕获鼠标按下事…...

宇树科技,改名了!
提到国内具身智能和机器人领域的代表企业,那宇树科技(Unitree)必须名列其榜。 最近,宇树科技的一项新变动消息在业界引发了不少关注和讨论,即: 宇树向其合作伙伴发布了一封公司名称变更函称,因…...

怎么让Comfyui导出的图像不包含工作流信息,
为了数据安全,让Comfyui导出的图像不包含工作流信息,导出的图像就不会拖到comfyui中加载出来工作流。 ComfyUI的目录下node.py 直接移除 pnginfo(推荐) 在 save_images 方法中,删除或注释掉所有与 metadata …...

向量几何的二元性:叉乘模长与内积投影的深层联系
在数学与物理的空间世界中,向量运算构成了理解几何结构的基石。叉乘(外积)与点积(内积)作为向量代数的两大支柱,表面上呈现出截然不同的几何意义与代数形式,却在深层次上揭示了向量间相互作用的…...

2.2.2 ASPICE的需求分析
ASPICE的需求分析是汽车软件开发过程中至关重要的一环,它涉及到对需求进行详细分析、验证和确认,以确保软件产品能够满足客户和用户的需求。在ASPICE中,需求分析的关键步骤包括: 需求细化:将从需求收集阶段获得的高层需…...

13.10 LangGraph多轮对话系统实战:Ollama私有部署+情感识别优化全解析
LangGraph多轮对话系统实战:Ollama私有部署+情感识别优化全解析 LanguageMentor 对话式训练系统架构与实现 关键词:多轮对话系统设计、场景化提示工程、情感识别优化、LangGraph 状态管理、Ollama 私有化部署 1. 对话训练系统技术架构 采用四层架构实现高扩展性的对话训练…...

验证redis数据结构
一、功能验证 1.验证redis的数据结构(如字符串、列表、哈希、集合、有序集合等)是否按照预期工作。 2、常见的数据结构验证方法: ①字符串(string) 测试基本操作 set、get、incr、decr 验证字符串的长度和内容是否正…...

自定义线程池1.2
自定义线程池 1.2 1. 简介 上次我们实现了 1.1 版本,将线程池中的线程数量交给使用者决定,并且将线程的创建延迟到任务提交的时候,在本文中我们将对这个版本进行如下的优化: 在新建线程时交给线程一个任务。让线程在某种情况下…...
