leetcode-不同路径问题
一个机器人位于一个
m x n网格的左上角 (起始点在下图中标记为 “Start” )。机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish” )。
问总共有多少条不同的路径?
看见题目我们首先用动态规划四步曲进行分析。
dp数组应该怎么看?我们回想一下爬楼梯,其实本题和他也没什么区别,唯一不同的我们这个是二维的,既然要记录总共的路径那么我们就定义一个二维数组,每一个记录到该点要走多少步,和爬楼梯一样,他是只能走一步或者两步,我们是只能向下或者向右,所以我们每一点的值就等于他上面的和左边的和,毕竟他们俩是不重复的,加起来就是能到该点的所有的路径。
所以得到递推公式: dp[i][j] = dp[i-1][j]+dp[i][j-1];
那么我们怎么初始化呢,首先我们看一下递推公式,需要-1,那就意味着我们的第一行和第一列都是要初始化的,所以我们直接把他们赋值成1就可以了。
我们直接上代码
class Solution {public int uniquePaths(int m, int n) {int[][] dp = new int[m][n];for(int i = 0;i<m;i++){dp[i][0] = 1;for(int j = 0;j<n;j++){dp[0][j] = 1;}}for(int i = 1;i<m;i++){for(int j = 1;j<n;j++){dp[i][j] = dp[i-1][j]+dp[i][j-1];}}return dp[m-1][n-1];}
} 给定一个
m x n的整数数组grid。一个机器人初始位于 左上角(即grid[0][0])。机器人尝试移动到 右下角(即grid[m - 1][n - 1])。机器人每次只能向下或者向右移动一步。网格中的障碍物和空位置分别用
1和0来表示。机器人的移动路径中不能包含 任何 有障碍物的方格。返回机器人能够到达右下角的不同路径数量。
测试用例保证答案小于等于
2 * 109。示例 1:
输入:obstacleGrid = [[0,0,0],[0,1,0],[0,0,0]] 输出:2 解释:3x3 网格的正中间有一个障碍物。 从左上角到右下角一共有2条不同的路径: 1. 向右 -> 向右 -> 向下 -> 向下 2. 向下 -> 向下 -> 向右 -> 向右
这一题是上一题的变种,我们的路上有障碍了,我们如何规避这个障碍呢 ,首先就是在路程中把障碍物都变成让他没办法走,一开始我就只加了这一个逻辑,但是运行起来发现不对,后来我思考了一下发现还有问题,因为我们的初始化也有问题,如果第一排就有障碍,后面的都是0啊都得不到值,所以把这俩逻辑加进来这个问题就解决啦
class Solution {public int uniquePathsWithObstacles(int[][] obstacleGrid) {int m = obstacleGrid.length;int n = obstacleGrid[0].length;if (obstacleGrid[0][0] == 1) {return 0;}// 初始化 dp 数组int[][] dp = new int[m][n];dp[0][0] = 1; // 起点路径数为 1for (int j = 1; j < n; j++) {if (obstacleGrid[0][j] == 1) {break; // 遇到障碍物,后续路径都为 0}dp[0][j] = 1;}// 初始化第一列for (int i = 1; i < m; i++) {if (obstacleGrid[i][0] == 1) {break; // 遇到障碍物,后续路径都为 0}dp[i][0] = 1;}for (int i = 1; i < m; i++) {for (int j = 1; j < n; j++) {if (obstacleGrid[i][j] == 1) {dp[i][j] = 0; // 当前格子有障碍物,路径数为 0} else {dp[i][j] = dp[i - 1][j] + dp[i][j - 1]; // 状态转移}}}return dp[m - 1][n - 1];}
}相关文章:

leetcode-不同路径问题
一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。 机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish” )。 问总共有多少条不同的路径? 看见题目…...

MongoDB 数据库备份和恢复全攻略
在当今数据驱动的时代,数据库的稳定运行和数据安全至关重要。MongoDB 作为一款流行的 NoSQL 数据库,以其灵活的文档模型和高扩展性备受青睐。然而,无论数据库多么强大,数据丢失的风险始终存在,因此掌握 MongoDB 的备份…...

CentOS7使用源码安装PHP8教程整理
CentOS7使用源码安装PHP8教程整理 下载安装包解压下载的php tar源码包安装所需的一些依赖扩展库安装前的配置修改配置文件1、进入php8的安装包 配置环境变量开机自启启动服务创建软连接常见问题1、checking for icu-uc > 50.1 icu-io icu-i18n... no2、configure: error: Pa…...

Baklib助力内容中台实施的最佳实践与成功案例探索
内容概要 在当今数字化发展的背景下,内容中台的概念逐渐受到重视。内容中台不仅仅是一个技术平台,更是企业在内容管理和运营效率提升方面的重要助力。它通过整合内部资源,实现信息的集中管理与高效利用,帮助企业应对日益复杂的市…...

rocketmq-product-send方法源码分析
先看有哪些send方法 首先说红圈的 有3个红圈。归类成3种发送方式。假设前提条件,发送的topic,有3个broker,每个broker总共4个write队列,总共有12个队列。 普通发送。负载均衡12个队列。指定超时时间指定MessageQueue,发送&#…...

python flask中使用or查询和and查询,还有同时使用or、and的情况
在 Flask 中处理数据库查询时,通常会结合使用 ORM 工具,例如 SQLAlchemy。以下是 or 查询、and 查询以及两者同时使用的示例。 文章目录 基础准备1. 使用 or_ 查询2. 使用 and_ 查询3. 同时使用 or_ 和 and_4. 更加复杂的嵌套查询 基础准备 假设有一个…...
)
【第一天】零基础入门刷题Python-算法篇-数据结构与算法的介绍(持续更新)
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言一、Python数据结构与算法的详细介绍1.基本概念2.Python中的数据结构1. 列表(List)2. 元组(Tuple)3. 字典&#…...

租房管理系统实现智能化租赁提升用户体验与运营效率
内容概要 在当今快速发展的租赁市场中,租房管理系统的智能化转型显得尤为重要。它不仅帮助房东和租客之间建立更高效的沟通桥梁,还优化了整个租赁流程。通过智能化技术,这套系统能够自动处理资产管理、合同签署、财务管理等所有关键环节。这…...

python3+TensorFlow 2.x(四)反向传播
目录 反向传播算法 反向传播算法基本步骤: 反向中的参数变化 总结 反向传播算法 反向传播算法(Backpropagation)是训练人工神经网络时使用的一个重要算法,它是通过计算梯度并优化神经网络的权重来最小化误差。反向传播算法的核…...

Flutter 使用 flutter_inappwebview 加载 App 本地 HTML 文件
在 Flutter 开发中,加载本地 HTML 文件是一个常见的需求,尤其是在需要展示离线内容或自定义页面时。flutter_inappwebview 是一个功能强大的插件,支持加载本地文件和网络资源。本文将详细介绍如何使用 flutter_inappwebview 加载 App 本地 HT…...
Word常见问题:嵌入图片无法显示完整
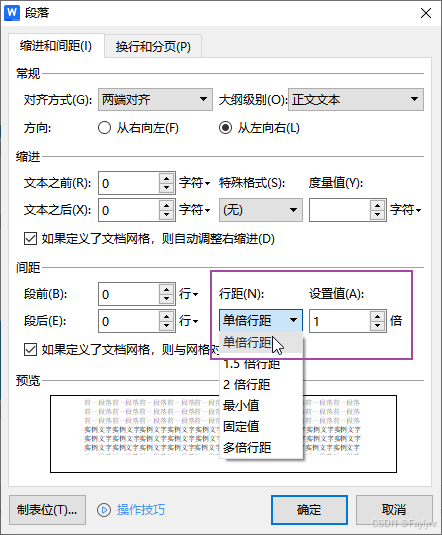
场景:在Word中,嵌入式图片显示不全,一部分图片在文字下方。如: 问题原因:因段落行距导致 方法一 快捷方式 选中图片,通过"ctrl1"快捷调整为1倍行距 方法二 通过工具栏调整 选中图片࿰…...

为AI聊天工具添加一个知识系统 之68 详细设计 之9 三种中台和时间度量 之1
本文要点 要点 在维度0上 被分离出来 的业务中台 需求、技术中台要求、和数据中台请求 (分别在时间层/空间层/时空层上 对应一个不同种类槽的容器,分别表示业务特征Feature[3]/技术方面Aspect[3]/数据流Fluent[3]) 在维度1~3的运动过程中 从…...

On to OpenGL and 3D computer graphics
2. On to OpenGL and 3D computer graphics 声明:该代码来自:Computer Graphics Through OpenGL From Theory to Experiments,仅用作学习参考 2.1 First Program Square.cpp完整代码 /// // square.cpp // // OpenGL program to draw a squ…...

从曾国藩的经历看如何打破成长中的瓶颈
《曾国藩传》是一部充满智慧与人生哲理的传记,而曾国藩本人更是一个从“最笨”到“最智慧”的奇人。看他的成长与蜕变,不仅能感受到他如何超越自己的局限,也能从中获得关于人性、社会和历史的重要启示。曾国藩的一生让人深思,正是…...
)
JavaWeb学习-SpringBotWeb开发入门(HTTP协议)
(一)SpringBotWeb开发步骤 (1)创建springboot工程,并勾选开发相关依赖 (2)定义HelloController类,添加方法hello,并添加注解 (3)运行测试 (二)HTTP入门概述 创建请求页面 package com.itheima.demo3; /*请求处理类,加上注解标识为请求处理类*/import org.spr…...

数据库用户管理
数据库用户管理 1.创建用户 MySQL在安装是,会默认创建一个名位root的用户,该用户拥有超级权限,可以控制整个MySQL服务器。 在对MySQL的日常管理和操作中,通常创建一些具有适当权限的用户,尽可能的不用或少用root登录…...

BGP边界网关协议(Border Gateway Protocol)路由聚合详解
一、路由聚合 1、意义 在大规模的网络中,BGP路由表十分庞大,给设备造成了很大的负担,同时使发生路由振荡的几率也大大增加,影响网络的稳定性。 路由聚合是将多条路由合并的机制,它通过只向对等体发送聚合后的路由而…...

ASP.NET Core WebAPI的异步及返回值
目录 Action方法的异步 Action方法参数 捕捉URL占位符 捕捉QueryString的值 JSON报文体 其他方式 Action方法的异步 Action方法既可以同步也可以异步。异步Action方法的名字一般不需要以Async结尾。Web API中Action方法的返回值如果是普通数据类型,那么返回值…...

「 机器人 」仿生扑翼飞行器中的“被动旋转机制”概述
前言 在仿生扑翼飞行器的机翼设计中,模仿昆虫翼的被动旋转机制是一项关键技术。其核心思想在于:机翼旋转角度(攻角)并非完全通过主动伺服来控制,而是利用空气动力和惯性力的作用,自然地实现被动调节。以下对这种设计的背景、原理与优势进行详细说明。 1. 背景:昆虫的被动…...

「 机器人 」扑翼飞行器的数据驱动建模核心方法
前言 数据驱动建模可充分利用扑翼飞行器的已有运行数据,改进动力学模型与控制策略,并对未建模动态做出更精确的预测。在复杂的非线性飞行环境中,该方法能有效弥补传统解析建模的不足,具有较高的研究与应用价值。以下针对主要研究方向和实现步骤进行整理与阐述。 1. 数据驱动…...
结构体的进阶应用)
基于算法竞赛的c++编程(28)结构体的进阶应用
结构体的嵌套与复杂数据组织 在C中,结构体可以嵌套使用,形成更复杂的数据结构。例如,可以通过嵌套结构体描述多层级数据关系: struct Address {string city;string street;int zipCode; };struct Employee {string name;int id;…...

浅谈 React Hooks
React Hooks 是 React 16.8 引入的一组 API,用于在函数组件中使用 state 和其他 React 特性(例如生命周期方法、context 等)。Hooks 通过简洁的函数接口,解决了状态与 UI 的高度解耦,通过函数式编程范式实现更灵活 Rea…...

django filter 统计数量 按属性去重
在Django中,如果你想要根据某个属性对查询集进行去重并统计数量,你可以使用values()方法配合annotate()方法来实现。这里有两种常见的方法来完成这个需求: 方法1:使用annotate()和Count 假设你有一个模型Item,并且你想…...

cf2117E
原题链接:https://codeforces.com/contest/2117/problem/E 题目背景: 给定两个数组a,b,可以执行多次以下操作:选择 i (1 < i < n - 1),并设置 或,也可以在执行上述操作前执行一次删除任意 和 。求…...

现代密码学 | 椭圆曲线密码学—附py代码
Elliptic Curve Cryptography 椭圆曲线密码学(ECC)是一种基于有限域上椭圆曲线数学特性的公钥加密技术。其核心原理涉及椭圆曲线的代数性质、离散对数问题以及有限域上的运算。 椭圆曲线密码学是多种数字签名算法的基础,例如椭圆曲线数字签…...

OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别
OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别 直接训练提示词嵌入向量的核心区别 您提到的代码: prompt_embedding = initial_embedding.clone().requires_grad_(True) optimizer = torch.optim.Adam([prompt_embedding...

【JavaWeb】Docker项目部署
引言 之前学习了Linux操作系统的常见命令,在Linux上安装软件,以及如何在Linux上部署一个单体项目,大多数同学都会有相同的感受,那就是麻烦。 核心体现在三点: 命令太多了,记不住 软件安装包名字复杂&…...

AspectJ 在 Android 中的完整使用指南
一、环境配置(Gradle 7.0 适配) 1. 项目级 build.gradle // 注意:沪江插件已停更,推荐官方兼容方案 buildscript {dependencies {classpath org.aspectj:aspectjtools:1.9.9.1 // AspectJ 工具} } 2. 模块级 build.gradle plu…...

九天毕昇深度学习平台 | 如何安装库?
pip install 库名 -i https://pypi.tuna.tsinghua.edu.cn/simple --user 举个例子: 报错 ModuleNotFoundError: No module named torch 那么我需要安装 torch pip install torch -i https://pypi.tuna.tsinghua.edu.cn/simple --user pip install 库名&#x…...

【网络安全】开源系统getshell漏洞挖掘
审计过程: 在入口文件admin/index.php中: 用户可以通过m,c,a等参数控制加载的文件和方法,在app/system/entrance.php中存在重点代码: 当M_TYPE system并且M_MODULE include时,会设置常量PATH_OWN_FILE为PATH_APP.M_T…...

