代码随想录_栈与队列
栈与队列
232.用栈实现队列
232. 用栈实现队列
使用栈实现队列的下列操作:
push(x) – 将一个元素放入队列的尾部。
pop() – 从队列首部移除元素。
peek() – 返回队列首部的元素。
empty() – 返回队列是否为空。
思路: 定义两个栈: 入队栈, 出队栈, 控制出入栈顺序, 进入的元素倒两次就是原顺序
代码:
class MyQueue {Stack<Integer> in;Stack<Integer> out;public MyQueue() {in = new Stack<>();out = new Stack<>();}public void push(int x) {in.push(x);}public int pop() {inToOut();return out.pop();}public int peek() {inToOut();return out.peek();}private void inToOut() {// out非空时不能往里面倒, 出的时候要先把out里的出完, 再倒入// 否则原来的数据会被覆盖if(!out.isEmpty()) return;while(!in.isEmpty()) {out.push(in.pop());}}public boolean empty() {return in.isEmpty() && out.isEmpty();}
}
225. 用队列实现栈
225. 用队列实现栈
使用队列实现栈的下列操作:
- push(x) – 元素 x 入栈
- pop() – 移除栈顶元素
- top() – 获取栈顶元素
- empty() – 返回栈是否为空
思路: 每次pop, peek都要reposition
代码:
class MyStack {Queue<Integer> queue;public MyStack() {queue = new LinkedList<>();}public void push(int x) {queue.offer(x);}public int pop() {reposition();// 每次pop时将队列前size - 1个放到队列末尾return queue.poll();}public int top() {reposition();// 每次pop时将队列前size - 1个放到队列末尾int n = queue.poll();queue.offer(n);return n;}public boolean empty() {return queue.isEmpty();}private void reposition() {int size = queue.size();size--;while(size-- > 0) {queue.offer(queue.poll());}}
}
20. 有效的括号
20. 有效的括号
给定一个只包括 ‘(’,‘)’,‘{’,‘}’,‘[’,‘]’ 的字符串,判断字符串是否有效。
有效字符串需满足:
- 左括号必须用相同类型的右括号闭合。
- 左括号必须以正确的顺序闭合。
- 注意空字符串可被认为是有效字符串。
思路:
一共有三种情况:
-
字符串里左方向的括号多余了 ,所以不匹配。
-
括号没有多余,但是 括号的类型没有匹配上。
-
字符串里右方向的括号多余了,所以不匹配。
每一个左括号, 压入对应的右括号, 当开始遍历右括号时, 按照如下方式和栈中元素进行对比
代码:
class Solution {public boolean isValid(String s) {// 0. 剪枝int len = s.length();if(len % 2 != 0) return false;// 长度为奇数, 则一定不能匹配// 1. 初始化栈Stack<Character> stack = new Stack<>();// 2. 遍历每一个字符for(int i = 0;i < len;i++) {// 2.1 每一个左括号, 压入对应的右括号if(s.charAt(i) == '(') {stack.push(')');}else if(s.charAt(i) == '[') {stack.push(']');}else if(s.charAt(i) == '{') {stack.push('}');// 2.2 每一个右括号, 查看栈中对应的右括号是否相等}else if(stack.isEmpty() || s.charAt(i) != stack.peek()) {// 不能是s.pop,否则在判断时就会将元素弹出return false;}else {// 右括号匹配, 出栈stack.pop();}}// 3. 遍历完后, 查看栈中是否还有右括号(左括号多余)return stack.isEmpty();}
}
1047. 删除字符串中的所有相邻重复项
1047. 删除字符串中的所有相邻重复项
给出由小写字母组成的字符串 S,重复项删除操作会选择两个相邻且相同的字母,并删除它们。
在 S 上反复执行重复项删除操作,直到无法继续删除。
在完成所有重复项删除操作后返回最终的字符串。答案保证唯一。
示例:
- 输入:“abbaca”
- 输出:“ca”
- 解释:例如,在 “abbaca” 中,我们可以删除 “bb” 由于两字母相邻且相同,这是此时唯一可以执行删除操作的重复项。之后我们得到字符串 “aaca”,其中又只有 “aa” 可以执行重复项删除操作,所以最后的字符串为 “ca”。
法一: 栈
思路: 用字符串模拟栈(也可以直接用栈, 需要再转为字符串)进行"消消乐", 留下的就是最终的字符串
代码:
class Solution {public String removeDuplicates(String s) {// 1. 定义字符串模拟栈StringBuilder sb = new StringBuilder();// 2. 遍历s的每一位, 与栈进行消除int top = -1;for(int i = 0;i < s.length();i++) {if(top >= 0 && s.charAt(i) == sb.charAt(top)) {sb.deleteCharAt(top--);}else {sb.append(s.charAt(i));top++;}}// 3. 返回return sb.toString();}
}
法二:双指针
思路: 快指针指向原字符串要处理的字符, 慢指针指向新的字符串, 当新字符串出现相邻相等的情况, 则将两个同时排除, 回退到第一次出现该字符的位置, 继续遍历原字符串的下一个字符, 否则, 快慢指针同时往前走.
代码:
class Solution {public String removeDuplicates(String s) {// 1. 初始化char[] str = s.toCharArray();int fast = 0,slow = 0;// 2. 遍历原字符串while(fast < str.length) {str[slow] = str[fast++];// 2.1 新的字符串出现成对可消除, 走到第一次出现的位置, 覆盖(同时消除)if(slow > 0 && str[slow] == str[slow - 1]) {slow--;}else{// 2.2 没有可消除的字符, fast slow都往后走slow++;}}// 3. 返回return new String(str,0,slow);}
}
150. 逆波兰表达式求值
150. 逆波兰表达式求值
根据 逆波兰表示法,求表达式的值。
有效的运算符包括 + , - , * , / 。每个运算对象可以是整数,也可以是另一个逆波兰表达式。
说明:
整数除法只保留整数部分。 给定逆波兰表达式总是有效的。换句话说,表达式总会得出有效数值且不存在除数为 0 的情况。
示例 1:
- 输入: [“2”, “1”, “+”, “3”, " * "]
- 输出: 9
- 解释: 该算式转化为常见的中缀算术表达式为:((2 + 1) * 3) = 9
思路: 栈, 每遇到一个操作符, 就对栈中的两个数组进行计算, 注意: 栈中的顺序与原来后缀表达式计算顺序相反, 因此弹出来的两个数字运算时交换顺序注意: 栈中的顺序与原来后缀表达式计算顺序相反, 因此弹出来的两个数字运算时交换顺序.
代码:
class Solution {public int evalRPN(String[] tokens) {// 0. 剪枝if(tokens.length == 1) return Integer.valueOf(tokens[0]);// 1. 定义栈Stack<Integer> sk = new Stack<>();// 2. 逐个处理for(String s : tokens) {// 2.1 处理运算符if("+".equals(s) || "-".equals(s) || "*".equals(s) || "/".equals(s)) {// 注意: 栈中的顺序与原来后缀表达式计算顺序相反, 因此弹出来的两个数字运算时交换顺序int n = sk.pop();int m = sk.pop();if("+".equals(s)) {sk.push(m + n);}else if("-".equals(s)) {sk.push(m - n);}else if("*".equals(s)) {sk.push(m * n);}else if("/".equals(s)) {sk.push(m / n);}}else {// 2.2 处理数字sk.push(Integer.valueOf(s));}}// 3. 返回return sk.pop();}
}
239. 滑动窗口最大值
239. 滑动窗口最大值
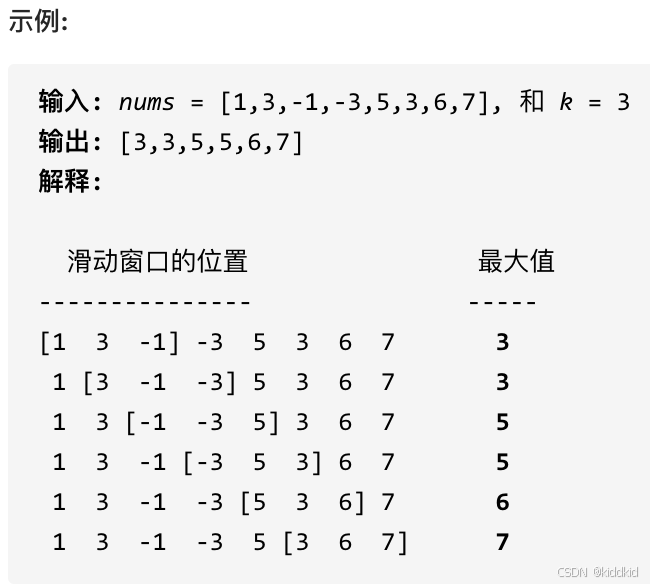
给定一个数组 nums,有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。
返回滑动窗口中的最大值。
进阶:
你能在线性时间复杂度内解决此题吗?
提示:
- 1 <= nums.length <= 10^5
- -10^4 <= nums[i] <= 10^4
- 1 <= k <= nums.length
思路: 单调队列, 保证队头为窗口内最大值, 保证每次队列内有不多于k个元素
代码:
class Solution {public int[] maxSlidingWindow(int[] nums, int k) {// 1. 定义容器ArrayDeque<Integer> q = new ArrayDeque<>();int n = nums.length,index = 0;int[] ans = new int[n - k + 1];// 2. 循环遍历for(int i = 0;i < n;i++) {// 2.1 出: 将不符合窗口范围的移出while(!q.isEmpty() && q.peek() < (i - k + 1)) q.poll();// 2.2 入: 先将比该数值小的从后往前依次移出(保证单调), 再放入while(!q.isEmpty() && nums[q.peekLast()] < nums[i]) q.pollLast();q.offer(i);// 2.3 收集: 当窗口中走够k个元素时, 开始收集if(i >= k - 1) ans[index++] = nums[q.peek()];}// 3. 返回return ans;}
}
347.前 K 个高频元素
347. 前 K 个高频元素
给定一个非空的整数数组,返回其中出现频率前 k 高的元素。
示例 1:
- 输入: nums = [1,1,1,2,2,3], k = 2
- 输出: [1,2]
示例 2:
- 输入: nums = [1], k = 1
- 输出: [1]
思路: map统计num及其出现次数, PriorityQueue用作小顶堆, 维护前k个出现次数最多的entry
代码:
class Solution {public int[] topKFrequent(int[] nums, int k) {// 1. 定义容器int[] ans = new int[k];Map<Integer,Integer> map = new HashMap<>();PriorityQueue<int[]> pq = new PriorityQueue<>((o1,o2) -> o1[1] - o2[1]);// 2. 填充mapfor(int num : nums) {map.put(num,map.getOrDefault(num,0) + 1);}// 3. 填充pqSet<Map.Entry<Integer,Integer>> entries = map.entrySet();for(Map.Entry<Integer,Integer> e : entries) {int[] t = new int[2];t[0] = e.getKey();t[1] = e.getValue();pq.offer(t);// 维持小顶堆中3个出现次数最多元素if(pq.size() > k) pq.poll();}// 4. 返回for(int i = 0;i < k;i++) {ans[i] = pq.poll()[0];}return ans;}
}
相关文章:

代码随想录_栈与队列
栈与队列 232.用栈实现队列 232. 用栈实现队列 使用栈实现队列的下列操作: push(x) – 将一个元素放入队列的尾部。 pop() – 从队列首部移除元素。 peek() – 返回队列首部的元素。 empty() – 返回队列是否为空。 思路: 定义两个栈: 入队栈, 出队栈, 控制出入…...

【微服务与分布式实践】探索 Sentinel
参数设置 熔断时长 、最小请求数、最大RT ms、比例阈值、异常数 熔断策略 慢调⽤⽐例 当单位统计时⻓内请求数⽬⼤于设置的最⼩请求数⽬,并且慢调⽤的⽐例⼤于阈值,则接下来的熔断时⻓内请求会⾃动被熔断 异常⽐例 当单位统计时⻓内请求数⽬⼤于设置…...
深入研究异常处理机制
一、原理探究 C异常处理 本节内容针对 Linux 下的 C 异常处理机制,重点在于研究如何在异常处理流程中利用溢出漏洞,所以不对异常处理及 unwind 的过程做详细分析,只做简单介绍 异常机制中主要的三个关键字:throw 抛出异常&#x…...

【memgpt】letta 课程4:基于latta框架构建MemGpt代理并与之交互
Lab 3: Building Agents with memory 基于latta框架构建MemGpt代理并与之交互理解代理状态,例如作为系统提示符、工具和agent的内存查看和编辑代理存档内存MemGPT 代理是有状态的 agents的设计思路 每个步骤都要定义代理行为 Letta agents persist information over time and…...

讯飞智作 AI 配音技术浅析(二):深度学习与神经网络
讯飞智作 AI 配音技术依赖于深度学习与神经网络,特别是 Tacotron、WaveNet 和 Transformer-TTS 模型。这些模型通过复杂的神经网络架构和数学公式,实现了从文本到自然语音的高效转换。 一、Tacotron 模型 Tacotron 是一种端到端的语音合成模型ÿ…...
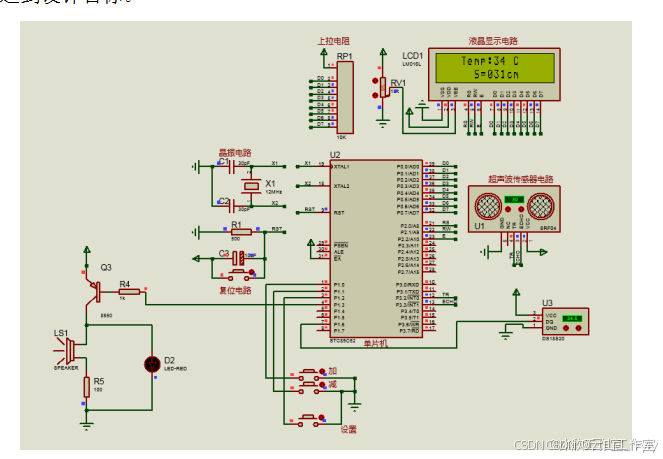
基于单片机的超声波液位检测系统(论文+源码)
1总体设计 本课题为基于单片机的超声波液位检测系统的设计,系统的结构框图如图2.1所示。其中包括了按键模块,温度检测模块,超声波液位检测模块,显示模块,蜂鸣器等器件设备。其中,采用STC89C52单片机作为主控…...

Autogen_core: test_code_executor.py
目录 代码代码解释 代码 import textwrapimport pytest from autogen_core.code_executor import (Alias,FunctionWithRequirements,FunctionWithRequirementsStr,ImportFromModule, ) from autogen_core.code_executor._func_with_reqs import build_python_functions_file f…...

从0开始使用面对对象C语言搭建一个基于OLED的图形显示框架
目录 前言 环境介绍 代码与动机 架构设计,优缺点 博客系列指引 前言 笔者前段时间花费了一周,整理了一下自从TM1637开始打算的,使用OLED来搭建一个通用的显示库的一个工程。笔者的OLED库已经开源到Github上了,地址在…...
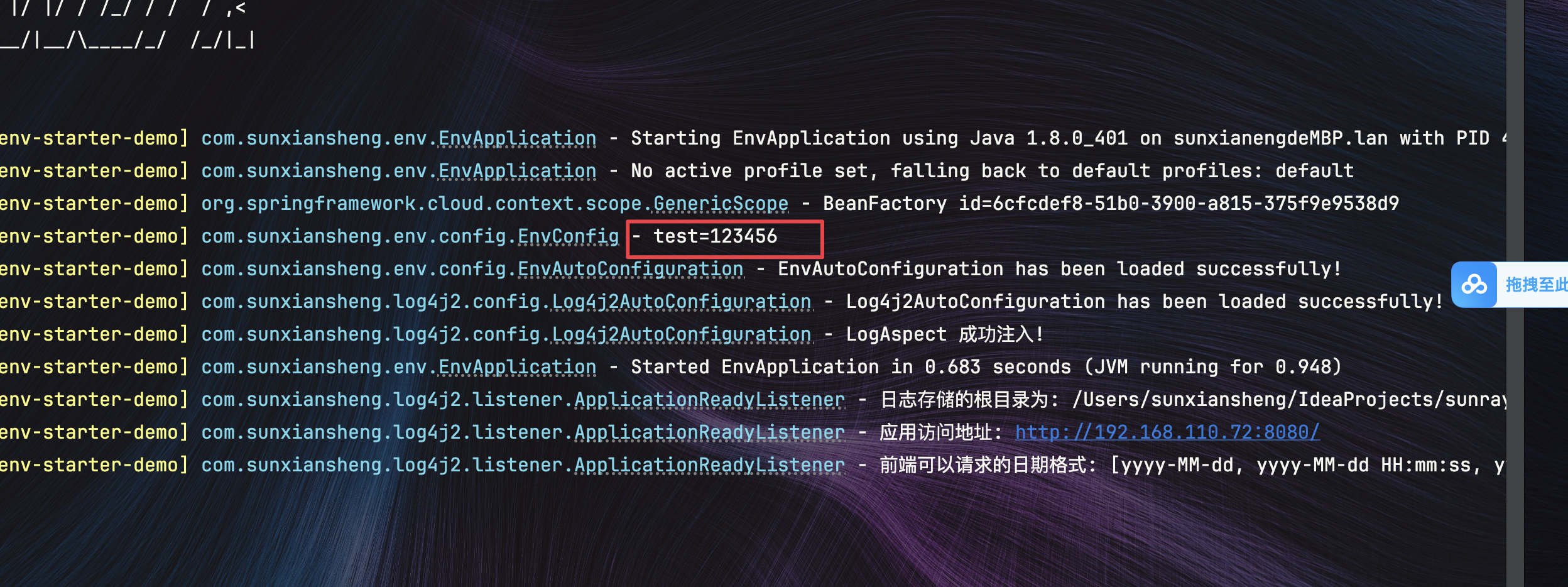
Java实现.env文件读取敏感数据
文章目录 1.common-env-starter模块1.目录结构2.DotenvEnvironmentPostProcessor.java 在${xxx}解析之前执行,提前读取配置3.EnvProperties.java 这里的path只是为了代码提示4.EnvAutoConfiguration.java Env模块自动配置类5.spring.factories 自动配置和注册Enviro…...

Go反射指南
概念: 官方对此有个非常简明的介绍,两句话耐人寻味: 反射提供一种让程序检查自身结构的能力反射是困惑的源泉 第1条,再精确点的描述是“反射是一种检查interface变量的底层类型和值的机制”。 第2条,很有喜感的自嘲…...
Fullcalendar @fullcalendar/react 样式错乱丢失问题和导致页面卡顿崩溃问题
问题描述: 我使用 fullcalendar的react版本时,出现了一个诡异的问题,当我切换到 一个iframe页面时(整个页面是一个iframe嵌入的),再切换回来日历的样式丢失了!不仅丢失了样式还导致页面崩溃了&…...
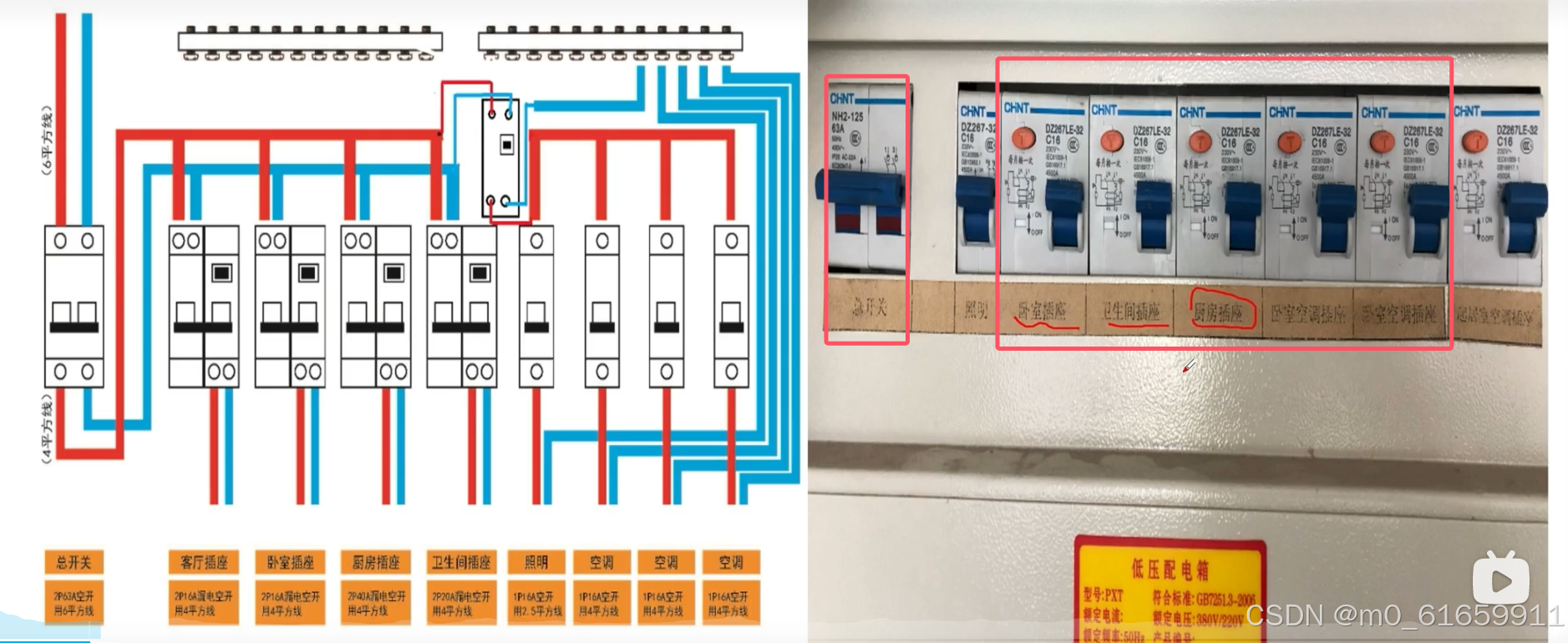
【电工基础】4.低压电器元件,漏电保护器,熔断器,中间继电器
一。漏电保护器 1.使用区域 我们在家用总开关上使用空气开关(断路器),其余的厨房卧室为漏电保护器。 2.漏电保护器的简介 1.漏电:就是流入的电流和流出的电流不等,意味着电路回路中还有其它分支,可能是电流通过人体进…...
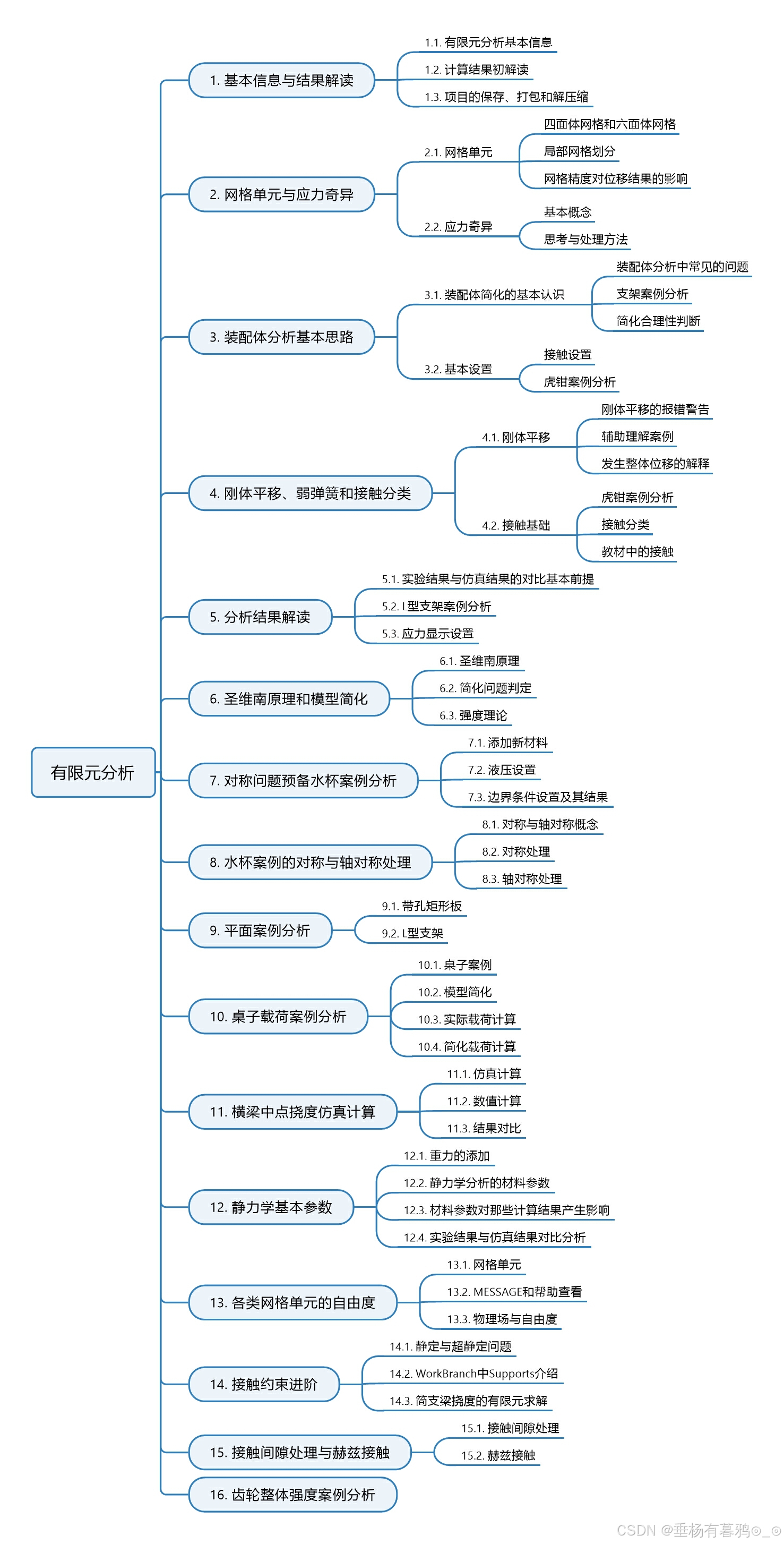
有限元分析学习——Anasys Workbanch第一阶段笔记梳理
第一阶段笔记主要源自于哔哩哔哩《ANSYS-workbench 有限元分析应用基础教程》 张晔 主要内容导图: 笔记导航如下: Anasys Workbanch第一阶段笔记(1)基本信息与结果解读_有限元分析变形比例-CSDN博客 Anasys Workbanch第一阶段笔记(2)网格单元与应力奇…...

C++中常用的十大排序方法之1——冒泡排序
成长路上不孤单😊😊😊😊😊😊 【😊///计算机爱好者😊///持续分享所学😊///如有需要欢迎收藏转发///😊】 今日分享关于C中常用的排序方法之——冒泡排序的相关…...
vscode+WSL2(ubuntu22.04)+pytorch+conda+cuda+cudnn安装系列
最近在家过年闲的没事,于是研究起深度学习开发工具链的配置和安装,之前欲与天公试比高,尝试在win上用vscodecuda11.6vs2019的cl编译器搭建cuda c编程环境,最后惨败,沦为笑柄,痛定思痛,这次直接和…...
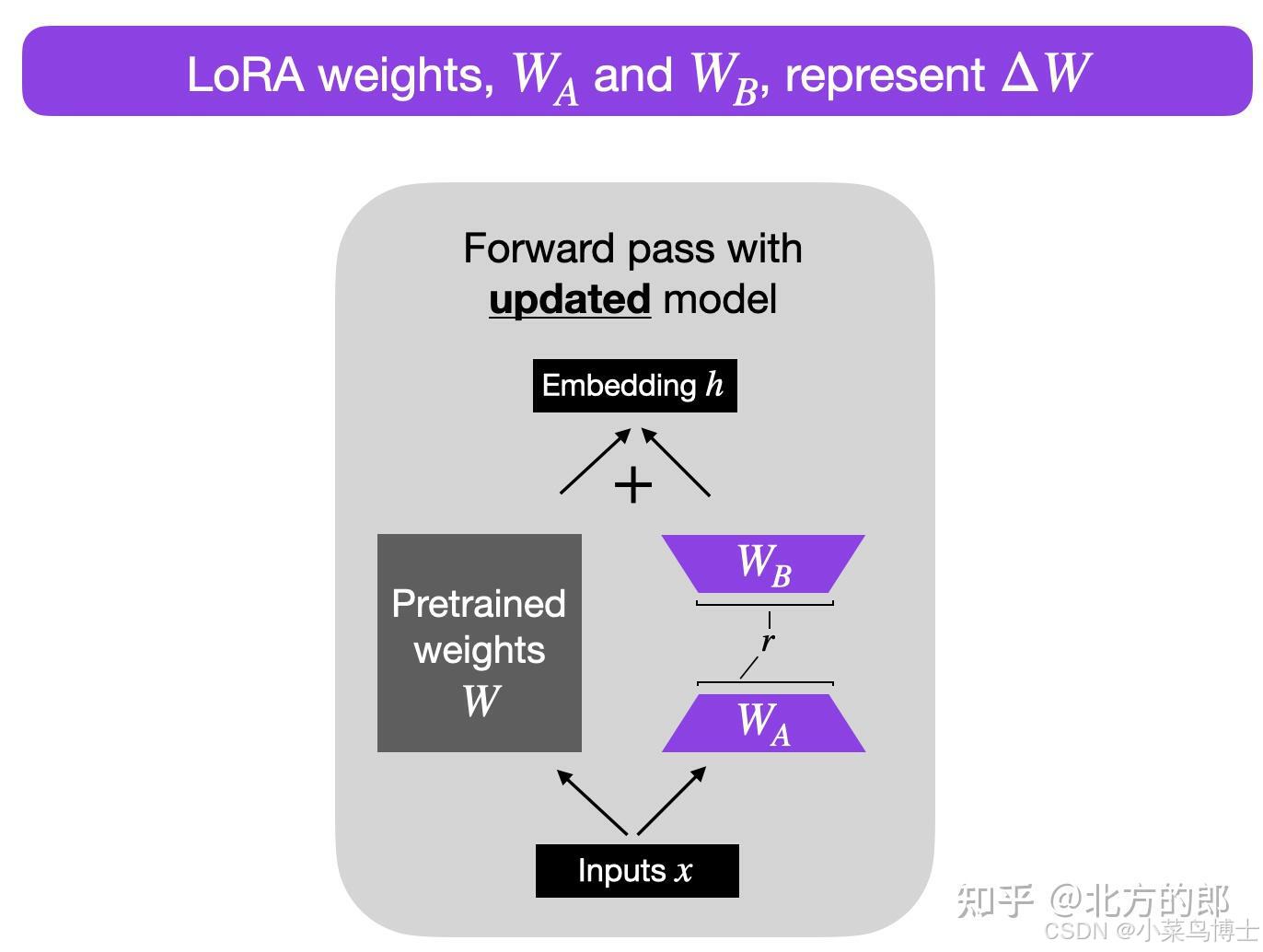
手撕Diffusion系列 - 第十一期 - lora微调 - 基于Stable Diffusion(代码)
手撕Diffusion系列 - 第十一期 - lora微调 - 基于Stable Diffusion(代码) 目录 手撕Diffusion系列 - 第十一期 - lora微调 - 基于Stable Diffusion(代码)Stable Diffusion 原理图Stable Diffusion的原理解释Stable Diffusion 和Di…...

【Block总结】OutlookAttention注意力,捕捉细节和局部特征|即插即用
论文信息 标题: VOLO: Vision Outlooker for Visual Recognition作者: Li Yuan, Qibin Hou, Zihang Jiang, Jiashi Feng, Shuicheng Yan代码链接: https://github.com/sail-sg/volo论文链接: https://arxiv.org/pdf/2106.13112 创新点 前景注意力机制: VOLO引入了一种称为“…...

网络攻防实战指北专栏讲解大纲与网络安全法
专栏 本专栏为网络攻防实战指北,大纲如下所示 进度:目前已更完准备篇、HTML基础 计划:所谓基础不牢,地动山摇。所以下一步将持续更新基础篇内容 讲解信息安全时,结合《中华人民共和国网络安全法》(以下简…...

【已解决】windows7虚拟机安装VMtools频繁报错
为了在虚拟机VMware中安装win7,题主先在网上下载了windows7 professional版本的镜像,在vmware中安装vmtools时报错,信息如下 (安装程序无法继续,本程序需要您将此虚拟机上安装的操作系统更新到SP1) 然后就…...

蓝桥杯模拟算法:多项式输出
P1067 [NOIP2009 普及组] 多项式输出 - 洛谷 | 计算机科学教育新生态 这道题是一道模拟题,我们需要分情况讨论,我们需要做一下分类讨论 #include <iostream> #include <cstdlib> using namespace std;int main() {int n;cin >> n;for…...

Lombok 的 @Data 注解失效,未生成 getter/setter 方法引发的HTTP 406 错误
HTTP 状态码 406 (Not Acceptable) 和 500 (Internal Server Error) 是两类完全不同的错误,它们的含义、原因和解决方法都有显著区别。以下是详细对比: 1. HTTP 406 (Not Acceptable) 含义: 客户端请求的内容类型与服务器支持的内容类型不匹…...

关于nvm与node.js
1 安装nvm 安装过程中手动修改 nvm的安装路径, 以及修改 通过nvm安装node后正在使用的node的存放目录【这句话可能难以理解,但接着往下看你就了然了】 2 修改nvm中settings.txt文件配置 nvm安装成功后,通常在该文件中会出现以下配置&…...

Frozen-Flask :将 Flask 应用“冻结”为静态文件
Frozen-Flask 是一个用于将 Flask 应用“冻结”为静态文件的 Python 扩展。它的核心用途是:将一个 Flask Web 应用生成成纯静态 HTML 文件,从而可以部署到静态网站托管服务上,如 GitHub Pages、Netlify 或任何支持静态文件的网站服务器。 &am…...

Java 加密常用的各种算法及其选择
在数字化时代,数据安全至关重要,Java 作为广泛应用的编程语言,提供了丰富的加密算法来保障数据的保密性、完整性和真实性。了解这些常用加密算法及其适用场景,有助于开发者在不同的业务需求中做出正确的选择。 一、对称加密算法…...

NLP学习路线图(二十三):长短期记忆网络(LSTM)
在自然语言处理(NLP)领域,我们时刻面临着处理序列数据的核心挑战。无论是理解句子的结构、分析文本的情感,还是实现语言的翻译,都需要模型能够捕捉词语之间依时序产生的复杂依赖关系。传统的神经网络结构在处理这种序列依赖时显得力不从心,而循环神经网络(RNN) 曾被视为…...

第 86 场周赛:矩阵中的幻方、钥匙和房间、将数组拆分成斐波那契序列、猜猜这个单词
Q1、[中等] 矩阵中的幻方 1、题目描述 3 x 3 的幻方是一个填充有 从 1 到 9 的不同数字的 3 x 3 矩阵,其中每行,每列以及两条对角线上的各数之和都相等。 给定一个由整数组成的row x col 的 grid,其中有多少个 3 3 的 “幻方” 子矩阵&am…...

全面解析各类VPN技术:GRE、IPsec、L2TP、SSL与MPLS VPN对比
目录 引言 VPN技术概述 GRE VPN 3.1 GRE封装结构 3.2 GRE的应用场景 GRE over IPsec 4.1 GRE over IPsec封装结构 4.2 为什么使用GRE over IPsec? IPsec VPN 5.1 IPsec传输模式(Transport Mode) 5.2 IPsec隧道模式(Tunne…...

技术栈RabbitMq的介绍和使用
目录 1. 什么是消息队列?2. 消息队列的优点3. RabbitMQ 消息队列概述4. RabbitMQ 安装5. Exchange 四种类型5.1 direct 精准匹配5.2 fanout 广播5.3 topic 正则匹配 6. RabbitMQ 队列模式6.1 简单队列模式6.2 工作队列模式6.3 发布/订阅模式6.4 路由模式6.5 主题模式…...

JVM 内存结构 详解
内存结构 运行时数据区: Java虚拟机在运行Java程序过程中管理的内存区域。 程序计数器: 线程私有,程序控制流的指示器,分支、循环、跳转、异常处理、线程恢复等基础功能都依赖这个计数器完成。 每个线程都有一个程序计数…...

MySQL 索引底层结构揭秘:B-Tree 与 B+Tree 的区别与应用
文章目录 一、背景知识:什么是 B-Tree 和 BTree? B-Tree(平衡多路查找树) BTree(B-Tree 的变种) 二、结构对比:一张图看懂 三、为什么 MySQL InnoDB 选择 BTree? 1. 范围查询更快 2…...
