数据结构---图的遍历
图的遍历(Travering Graph):从图的某一顶点出发,访遍图中的其余顶点,且每个顶点仅被访问一次,图的遍历算法是各种图的操作的基础。
复杂性:图的任意顶点可能和其余的顶点相邻接,可能在访问了某个顶点后,沿某条路径搜索后又回到原顶点。
解决办法:在遍历过程中记下已被访问过的顶点。设置一个辅助向量 Visited[1…nl(n为顶点数),其初值为0,一旦访问了顶点v后,使Visited[li]为1或为访问的次序号。
深度优先搜索(Depth First Search – DFS)
深度优先搜索(Depth-First Search,DFS) 是一种遍历或搜索树或图的算法。其基本思想是:从起始节点出发,沿着每一条路径一直走下去,直到无法继续为止,再回溯到最近的分叉点,继续沿着另一条路径走。这样递归地进行,直到所有节点都被访问到。
- DFS 适用于树和图这两种数据结构。DFS 的搜索方式“深度优先”,即尽量深入每一条路径,直到没有更多节点可以访问,再回溯并继续遍历其他路径。
DFS 工作流程
1.从起始节点开始:选择一个未被访问的节点作为起始节点。
2.访问当前节点:首先标记该节点为已访问,并处理该节点(例如打印或执行其他操作)。
3.递归访问邻居节点:然后继续访问该节点的一个未被访问的邻居节点,递归进行深度优先搜索。
4.回溯:当所有邻居节点都已经访问过时,回溯到上一个节点,继续探索其他未访问的邻居节点。
5.结束条件:直到所有节点都被访问过为止,DFS 完成。
深度优先搜索的特征:
1.递归:DFS 最自然的实现方式是递归。
2.回溯:DFS 通过回溯的方式,重新返回到上一个节点,继续探索。
3.栈结构:DFS 也可以通过显式栈来实现,栈结构符合 DFS 中的“后进先出”(LIFO)特性。
4.图的遍历:DFS 可以遍历图中的所有节点和边,适用于查找图的连通性、寻找环等问题。
DFS遍历下图C语言示例:
0/ \1 2/ \
3 4
#include <stdio.h>
#include <stdbool.h>#define MAX_VERTICES 5 // 最大顶点数(本例中为 5)// 图的邻接矩阵表示
int graph[MAX_VERTICES][MAX_VERTICES];// visited 数组用于记录顶点是否被访问过
bool visited[MAX_VERTICES];// 深度优先搜索函数
void dfs(int vertex, int n) {// 标记当前顶点为已访问visited[vertex] = true;printf("%d ", vertex);// 遍历所有相邻的顶点for (int i = 0; i < n; i++) {if (graph[vertex][i] == 1 && !visited[i]) {dfs(i, n); // 递归访问相邻的未访问顶点}}
}int main() {int n = 5; // 顶点数int m = 4; // 边数// 初始化图的邻接矩阵和 visited 数组for (int i = 0; i < n; i++) {for (int j = 0; j < n; j++) {graph[i][j] = 0;}visited[i] = false;}// 输入图的边(无向图)graph[0][1] = 1; graph[1][0] = 1; // 0-1graph[0][2] = 1; graph[2][0] = 1; // 0-2graph[1][3] = 1; graph[3][1] = 1; // 1-3graph[1][4] = 1; graph[4][1] = 1; // 1-4// 从顶点 0 开始进行 DFSprintf("深度优先搜索的结果:\n");dfs(0, n);return 0;
}广度优先搜索(Breadth First Search – BFS)
广度优先搜索(Breadth-First Search,BFS) 是一种图遍历算法,它从图的起始节点开始,首先访问该节点的所有邻居,然后访问这些邻居的邻居,依此类推,直到所有节点都被访问。
与**深度优先搜索(DFS)**不同,BFS 的搜索顺序是“广度优先”的,即先访问离起始节点较近的节点,然后逐渐向远离起始节点的地方扩展。
BFS 的核心思想是:
1.从起始节点开始,先访问当前节点的所有邻居。
2.将这些邻居节点按顺序加入一个队列。
3.然后从队列中取出下一个节点,访问该节点的所有未被访问过的邻居。
4.将这些邻居节点加入队列中,继续重复该过程,直到所有节点都被访问过为止。
BFS 的工作流程
1.初始化:首先,将起始节点加入队列,并标记为已访问。
2.队列操作:从队列中取出一个节点,访问它,并将该节点的所有未被访问的邻居加入队列。
3.重复操作:重复步骤 2,直到队列为空为止。
BFS 关键点:
1.队列(Queue):BFS 使用队列来存储待访问的节点,队列保证了“先进先出”(FIFO)的顺序。
2.层次遍历:BFS 会按层次逐级访问图中的节点,层与层之间是按距离起始节点的远近来定义的。
3.适用于无权图的最短路径:BFS 能在无权图中找到从起始节点到目标节点的最短路径。
示例BFS遍历下图
0/ \1 2/ \
3 4
#include <stdio.h>
#include <stdbool.h>
#include <stdlib.h>#define MAX_VERTICES 5 // 最大顶点数(本例中为 5)
#define MAX_QUEUE_SIZE 100 // 队列的最大大小// 图的邻接矩阵表示
int graph[MAX_VERTICES][MAX_VERTICES];// visited 数组用于记录顶点是否被访问过
bool visited[MAX_VERTICES];// 队列结构
typedef struct {int items[MAX_QUEUE_SIZE];int front;int rear;
} Queue;// 初始化队列
void initQueue(Queue* q) {q->front = -1;q->rear = -1;
}// 判断队列是否为空
int isEmpty(Queue* q) {return q->front == -1;
}// 队列入队
void enqueue(Queue* q, int value) {if (q->rear == MAX_QUEUE_SIZE - 1) {printf("队列已满!\n");return;}if (q->front == -1) {q->front = 0;}q->rear++;q->items[q->rear] = value;
}// 队列出队
int dequeue(Queue* q) {if (isEmpty(q)) {printf("队列为空!\n");return -1;}int value = q->items[q->front];q->front++;if (q->front > q->rear) {q->front = q->rear = -1; // 队列为空}return value;
}// 广度优先搜索(BFS)函数
void bfs(int startVertex, int n) {Queue q;initQueue(&q);// 将起始顶点入队,并标记为已访问visited[startVertex] = true;enqueue(&q, startVertex);while (!isEmpty(&q)) {int currentVertex = dequeue(&q);printf("%d ", currentVertex);// 遍历当前顶点的所有相邻顶点for (int i = 0; i < n; i++) {if (graph[currentVertex][i] == 1 && !visited[i]) {visited[i] = true; // 标记相邻顶点为已访问enqueue(&q, i); // 将未访问的相邻顶点入队}}}
}int main() {int n = 5; // 顶点数int m = 4; // 边数// 初始化图的邻接矩阵和 visited 数组for (int i = 0; i < n; i++) {for (int j = 0; j < n; j++) {graph[i][j] = 0;}visited[i] = false;}// 输入图的边(无向图)graph[0][1] = 1; graph[1][0] = 1; // 0-1graph[0][2] = 1; graph[2][0] = 1; // 0-2graph[1][3] = 1; graph[3][1] = 1; // 1-3graph[1][4] = 1; graph[4][1] = 1; // 1-4// 从顶点 0 开始进行 BFSprintf("广度优先搜索的结果:\n");bfs(0, n);return 0;
}
BFS 与 DFS 的区别:
DFS(深度优先搜索) 是“深度优先”,BFS 是“广度优先”。
DFS 会一直沿着一条路径走下去,直到没有未访问的邻居,之后才会回溯;BFS 则是逐层访问,保证了先访问起始节点的所有邻居,再访问下一层。
BFS 在无权图中可以保证找到最短路径,而 DFS 不一定。
在图论中,**最小生成树(Minimum Spanning Tree,MST) **是一个无向连通加权图的生成树,其边的权重之和最小。生成树是图的一部分,它包含图中所有的节点,并且是一个树结构(无环连通图)。
最小生成树边与点的关系:最小生成树的顶点数n与边数e之间的关系:n=e+1
普里姆算法(Prim)算法
Prim 算法 是一种贪心算法,用来求解图的最小生成树。它从一个节点出发,逐步选择最小权重的边,直到图中的所有节点都被包含在内。与 Kruskal 算法 相比,Prim 算法更适用于稠密图。
Prim 算法的基本思想:
1.从图的任意一个节点开始,加入最小生成树的集合。
2.在已加入的节点集合所相连的边中,选择一条最小权重的边,将其相邻的节点加入集合。
3.重复步骤 2,直到所有节点都被加入最小生成树中。




#include <stdio.h>
#include <limits.h> // 包含 INT_MAX#define MAX_VERTICES 5 // 图中的顶点数// 图的邻接矩阵表示(用 -1 表示没有边)
int graph[MAX_VERTICES][MAX_VERTICES] = {{0, 2, 3, 4, -1},{2, 0, -1, 5, -1},{3, -1, 0, 1, -1},{4, 5, 1, 0, -1},{-1, -1, -1, -1, 0}
};// Prim 算法函数
void prim(int n) {int parent[MAX_VERTICES]; // 存储最小生成树的父节点int key[MAX_VERTICES]; // 存储每个顶点到生成树的最小边权值int inMST[MAX_VERTICES]; // 判断顶点是否在最小生成树中// 初始化所有值for (int i = 0; i < n; i++) {key[i] = INT_MAX; // 关键值初始化为无穷大inMST[i] = 0; // 所有顶点都不在最小生成树中parent[i] = -1; // 没有父节点}key[0] = 0; // 从顶点 0 开始for (int count = 0; count < n - 1; count++) {// 选择一个最小权值的顶点int u = -1;int min = INT_MAX;for (int v = 0; v < n; v++) {if (!inMST[v] && key[v] < min) {min = key[v];u = v;}}// 将选择的顶点 u 加入最小生成树inMST[u] = 1;// 更新与 u 相邻的顶点的关键值for (int v = 0; v < n; v++) {// graph[u][v] != -1 表示 u 和 v 之间有边if (graph[u][v] != -1 && !inMST[v] && graph[u][v] < key[v]) {key[v] = graph[u][v];parent[v] = u;}}}// 输出最小生成树的边和权值printf("最小生成树的边和权值:\n");for (int i = 1; i < n; i++) {printf("%d - %d: %d\n", parent[i], i, graph[i][parent[i]]);}
}int main() {int n = 5; // 图中的顶点数prim(n); // 调用 Prim 算法return 0;
}克鲁斯卡尔(Kruskal)算法
Kruskal 算法 是求解最小生成树的另一种经典算法。它是一个贪心算法,选择图中权重最小的边,将它们逐步添加到生成树中,确保每次添加的边不会形成环。Kruskal 算法非常适合用于稀疏图。
Kruskal 算法的基本思想
1.排序:将图中的所有边按边的权重进行升序排序。
2.并查集:使用并查集(Union-Find)数据结构来判断添加边后是否形成环。若添加的边连接了两个不同的连通分量,则将这两个分量合并;若它们已经在同一个连通分量中,则跳过这条边。
3.构建最小生成树:从排序后的边中依次选择,若选择的边不形成环,则将其添加到最小生成树中,直到最小生成树中包含 V-1 条边(V 是节点的数量)。






#include <stdio.h>
#include <stdlib.h>#define MAX_VERTICES 5 // 顶点数// 边的结构体
typedef struct {int u, v, weight;
} Edge;// 并查集的数据结构
int parent[MAX_VERTICES];
int rank[MAX_VERTICES];// 初始化并查集
void initUnionFind(int n) {for (int i = 0; i < n; i++) {parent[i] = i; // 每个顶点的父节点初始化为自己rank[i] = 0; // 初始秩为 0}
}// 查找操作(带路径压缩)
int find(int x) {if (parent[x] != x) {parent[x] = find(parent[x]); // 路径压缩}return parent[x];
}// 合并操作(按秩合并)
void unionSets(int x, int y) {int rootX = find(x);int rootY = find(y);if (rootX != rootY) {// 按秩合并if (rank[rootX] > rank[rootY]) {parent[rootY] = rootX;} else if (rank[rootX] < rank[rootY]) {parent[rootX] = rootY;} else {parent[rootY] = rootX;rank[rootX]++;}}
}// 比较函数,用于按权值升序排序边
int compare(const void* a, const void* b) {return ((Edge*)a)->weight - ((Edge*)b)->weight;
}// 克鲁斯卡尔算法
void kruskal(Edge edges[], int n, int m) {// 初始化并查集initUnionFind(n);// 排序边qsort(edges, m, sizeof(Edge), compare);int mstWeight = 0;printf("最小生成树的边和权值:\n");// 遍历所有边,选择不形成环的边for (int i = 0; i < m; i++) {int u = edges[i].u;int v = edges[i].v;int weight = edges[i].weight;if (find(u) != find(v)) {unionSets(u, v);printf("%d - %d: %d\n", u, v, weight);mstWeight += weight;}}printf("最小生成树的总权值:%d\n", mstWeight);
}int main() {// 图的边(每条边包含两个顶点和边的权值)Edge edges[] = {{0, 1, 2},{0, 2, 3},{0, 3, 4},{1, 3, 5},{2, 3, 1}};int n = 5; // 顶点数int m = 5; // 边数// 调用克鲁斯卡尔算法kruskal(edges, n, m);return 0;
}迪杰斯特拉(Dijkstra)算法




#include <stdio.h>
#include <limits.h> // 包含 INT_MAX,表示无穷大
#include <stdbool.h>#define MAX_VERTICES 6 // 顶点数// 图的邻接矩阵表示
int graph[MAX_VERTICES][MAX_VERTICES] = {{0, 7, -1, 9, 9, -1},{7, 0, 5, 6, -1, -1},{-1, 5, 0, -1, -1, 8},{9, 6, -1, 0, 4, 1},{9, -1, -1, 4, 0, 3},{-1, -1, 8, 1, 3, 0}
};// 迪杰斯特拉算法
void dijkstra(int start, int n) {int dist[MAX_VERTICES]; // 存储起点到各个顶点的最短距离bool visited[MAX_VERTICES]; // 标记顶点是否已访问过// 初始化for (int i = 0; i < n; i++) {dist[i] = INT_MAX; // 设置初始距离为无穷大visited[i] = false; // 标记所有顶点为未访问}dist[start] = 0; // 起点到自身的距离为 0for (int count = 0; count < n - 1; count++) {// 在未访问的顶点中找到最小的距离int u = -1;int minDist = INT_MAX;for (int v = 0; v < n; v++) {if (!visited[v] && dist[v] < minDist) {minDist = dist[v];u = v;}}// 标记该顶点为已访问visited[u] = true;// 更新与 u 相邻的顶点的距离for (int v = 0; v < n; v++) {if (graph[u][v] != -1 && !visited[v] && dist[u] + graph[u][v] < dist[v]) {dist[v] = dist[u] + graph[u][v]; // 更新最短距离}}}// 输出最短路径printf("从顶点 %d 到其他顶点的最短路径为:\n", start);for (int i = 0; i < n; i++) {if (dist[i] == INT_MAX) {printf("%d 到 %d: 无路径\n", start, i);} else {printf("%d 到 %d: %d\n", start, i, dist[i]);}}
}int main() {int n = 6; // 图中的顶点数int start = 0; // 起点选择 0// 调用 Dijkstra 算法dijkstra(start, n);return 0;
}我们一天天地活着并不是理所当然,而是莫大的奇迹。归根结底,连我们此刻的心脏搏动都是一种奇迹。 —星野道夫
相关文章:

数据结构---图的遍历
图的遍历(Travering Graph):从图的某一顶点出发,访遍图中的其余顶点,且每个顶点仅被访问一次,图的遍历算法是各种图的操作的基础。 复杂性:图的任意顶点可能和其余的顶点相邻接,可能在访问了某个顶点后,沿某条路径搜索…...

Qwen 模型自动构建知识图谱,生成病例 + 评价指标优化策略
关于数据库和检索方式的选择 AI Medical Consultant for Visual Question Answering (VQA) 系统:更适合在前端使用向量数据库(如FAISS)结合关系型数据库来实现图像和文本的检索与存储。因为在 VQA 场景中,你需要对患者上传的图像或…...

.Net Web API 访问权限限定
看到一个代码是这样的: c# webapi 上 [Route("api/admin/file-service"), AuthorizeAdmin] AuthorizeAdmin 的定义是这样的 public class AuthorizeAdminAttribute : AuthorizeAttribute {public AuthorizeAdminAttribute(){Roles "admin"…...

项目架构调整,切换版本并发布到中央仓库
文章目录 0.完成运维篇maven发布到中央仓库的部分1.配置server到settings.xml2.配置gpg 1.架构调整1.sunrays-dependencies(统一管理依赖和配置)1.作为单独的模块2.填写发布到中央仓库的配置1.基础属性2.基本配置3.插件配置 3.完整的pom.xml 2.sunrays-f…...

考试知识点位运算
深入理解位运算 在C编程的世界里,位运算作为一种直接对二进制位进行操作的运算方式,虽然不像加减乘除等算术运算那样广为人知,却在许多关键领域发挥着至关重要的作用。从底层系统开发到高效算法设计,位运算都展现出其独特的魅力与…...
-- 数据处理与可视化)
matlab快速入门(2)-- 数据处理与可视化
MATLAB的数据处理 1. 数据导入与导出 (1) 从文件读取数据 Excel 文件:data readtable(data.xlsx); % 读取为表格(Table)CSV 文件:data readtable(data.csv); % 自动处理表头和分隔符文本文件:data load(data.t…...

Kafka中文文档
文章来源:https://kafka.cadn.net.cn 什么是事件流式处理? 事件流是人体中枢神经系统的数字等价物。它是 为“永远在线”的世界奠定技术基础,在这个世界里,企业越来越多地使用软件定义 和 automated,而软件的用户更…...

Python-列表
3.1 列表是什么 在Python中,列表是一种非常重要的数据结构,用于存储一系列有序的元素。列表中的每个元素都有一个索引,索引从0开始。列表可以包含任何类型的元素,包括其他列表。 # 创建一个列表my_list [1, 2, 3, four, 5.0]…...

51单片机开发:定时器中断
目标:利用定时器中断,每隔1s开启/熄灭LED1灯。 外部中断结构图如下图所示,要使用定时器中断T0,须开启TE0、ET0。: 系统中断号如下图所示:定时器0的中断号为1。 定时器0的工作方式1原理图如下图所示&#x…...

【HarmonyOS之旅】基于ArkTS开发(三) -> 兼容JS的类Web开发(二)
目录 1 -> HML语法 1.1 -> 页面结构 1.2 -> 数据绑定 1.3 -> 普通事件绑定 1.4 -> 冒泡事件绑定5 1.5 -> 捕获事件绑定5 1.6 -> 列表渲染 1.7 -> 条件渲染 1.8 -> 逻辑控制块 1.9 -> 模板引用 2 -> CSS语法 2.1 -> 尺寸单位 …...

算法【混合背包】
混合背包是指多种背包模型的组合与转化。 下面通过题目加深理解。 题目一 测试链接:1742 -- Coins 分析:这道题可以通过硬币的个数将其转化为01背包,完全背包和多重背包。如果硬币的个数是1个,则是01背包;如果硬币的…...
)
WordPress eventon-lite插件存在未授权信息泄露漏洞(CVE-2024-0235)
免责声明: 本文旨在提供有关特定漏洞的深入信息,帮助用户充分了解潜在的安全风险。发布此信息的目的在于提升网络安全意识和推动技术进步,未经授权访问系统、网络或应用程序,可能会导致法律责任或严重后果。因此,作者不对读者基于本文内容所采取的任何行为承担责任。读者在…...

基于微信小程序的医院预约挂号系统设计与实现(LW+源码+讲解)
专注于大学生项目实战开发,讲解,毕业答疑辅导,欢迎高校老师/同行前辈交流合作✌。 技术范围:SpringBoot、Vue、SSM、HLMT、小程序、Jsp、PHP、Nodejs、Python、爬虫、数据可视化、安卓app、大数据、物联网、机器学习等设计与开发。 主要内容:…...

C++初阶 -- 手撕string类(模拟实现string类)
目录 一、string类的成员变量 二、构造函数 2.1 无参版本 2.2 有参版本 2.3 缺省值版本 三、析构函数 四、拷贝构造函数 五、c_str函数 六、operator重载 七、size函数 八、迭代器iterator 8.1 正常版本 8.2 const版本 九、operator[] 9.1 正常版本 9.2 const版…...

【Postman接口测试】Postman的安装和使用
在软件测试领域,接口测试是保障软件质量的关键环节之一,而Postman作为一款功能强大且广受欢迎的接口测试工具,能够帮助测试人员高效地进行接口测试工作。本文将详细介绍Postman的安装和使用方法,让你快速上手这款工具。 一、Pos…...
miniconda学习笔记
文章主要内容:演示miniconda切换不同python环境,安装python库,使用pycharm配置不同的conda建的python环境 目录 一、miniconda 1. 是什么? 2.安装miniconda 3.基本操作 一、miniconda 1. 是什么? miniconda是一个anac…...

区块链项目孵化与包装设计:从概念到市场的全流程指南
区块链技术的快速发展催生了大量创新项目,但如何将一个区块链项目从概念孵化成市场认可的产品,是许多团队面临的挑战。本文将从孵化策略、包装设计和市场落地三个维度,为你解析区块链项目成功的关键步骤。 一、区块链项目孵化的核心要素 明确…...

JavaScript的基本组成
1、JavaScript的组成部分 JavaScript可以分为三个部分:ECMAScript标准、DOM、BOM。 ECMAScript标准 即JS的基本语法,JavaScript的核心,描述了语言的基本语法和数据类型,ECMAScript是一套标 准,定义了一种语言…...
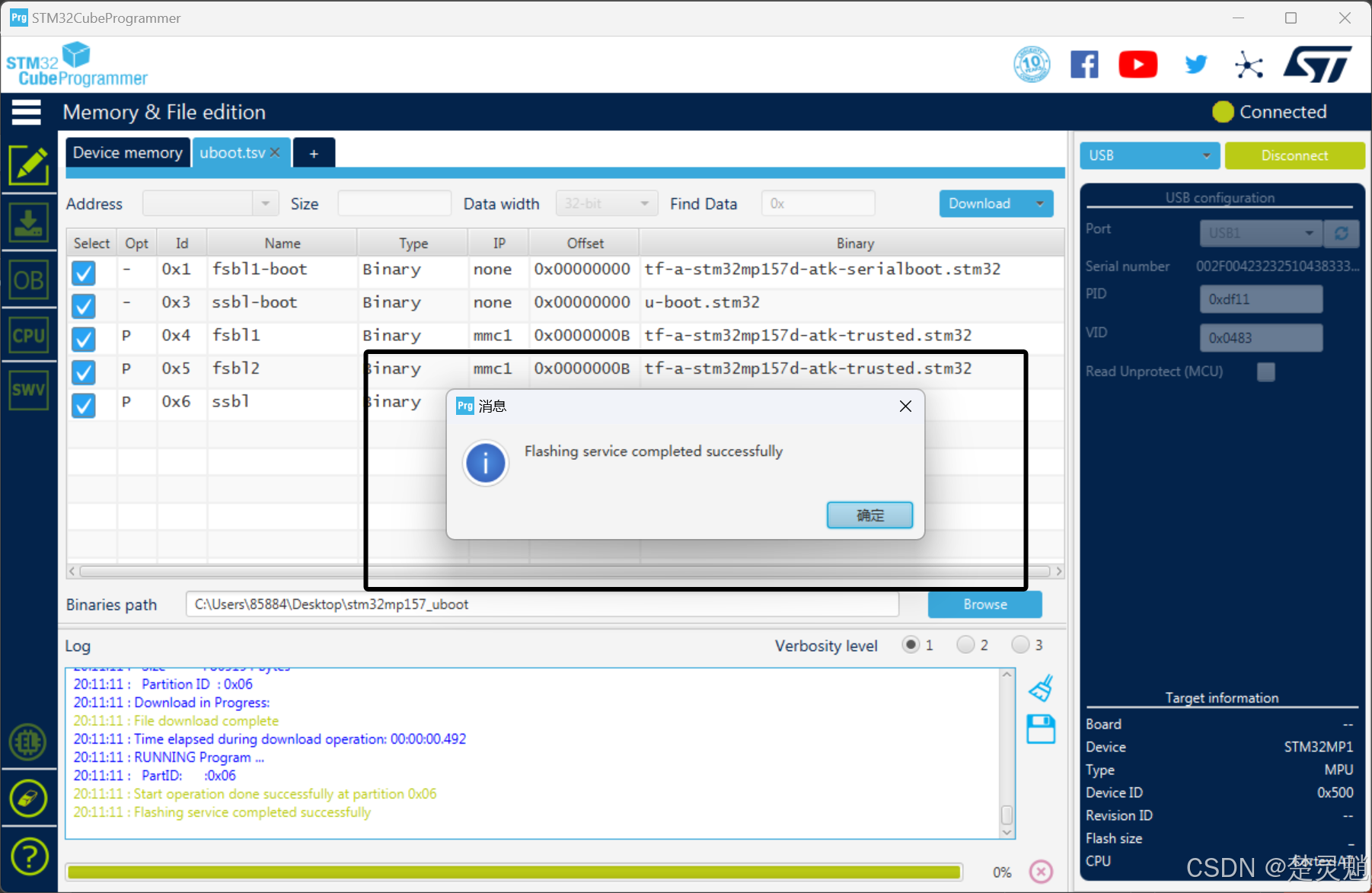
[Linux]从零开始的STM32MP157 U-Boot移植
一、前言 在上一次教程中,我们了解了STM32MP157的启动流程与安全启动机制。我们还将FSBL的相关代码移植成功了。大家还记得FSBL的下一个步骤是什么吗?没错,就是SSBL,而且常见的我们将SSBL作为存放U-Boot的地方。所以本次教程&…...

【Unity3D】实现横版2D游戏——攀爬绳索(简易版)
目录 GeneRope.cs 场景绳索生成类 HeroColliderController.cs 控制角色与单向平台是否忽略碰撞 HeroClampController.cs 控制角色攀爬 OnTriggerEnter2D方法 OnTriggerStay2D方法 OnTriggerExit2D方法 Update方法 开始攀爬 结束攀爬 Sensor_HeroKnight.cs 角色触发器…...
)
Java 语言特性(面试系列2)
一、SQL 基础 1. 复杂查询 (1)连接查询(JOIN) 内连接(INNER JOIN):返回两表匹配的记录。 SELECT e.name, d.dept_name FROM employees e INNER JOIN departments d ON e.dept_id d.dept_id; 左…...
)
进程地址空间(比特课总结)
一、进程地址空间 1. 环境变量 1 )⽤户级环境变量与系统级环境变量 全局属性:环境变量具有全局属性,会被⼦进程继承。例如当bash启动⼦进程时,环 境变量会⾃动传递给⼦进程。 本地变量限制:本地变量只在当前进程(ba…...

SCAU期末笔记 - 数据分析与数据挖掘题库解析
这门怎么题库答案不全啊日 来简单学一下子来 一、选择题(可多选) 将原始数据进行集成、变换、维度规约、数值规约是在以下哪个步骤的任务?(C) A. 频繁模式挖掘 B.分类和预测 C.数据预处理 D.数据流挖掘 A. 频繁模式挖掘:专注于发现数据中…...

iPhone密码忘记了办?iPhoneUnlocker,iPhone解锁工具Aiseesoft iPhone Unlocker 高级注册版分享
平时用 iPhone 的时候,难免会碰到解锁的麻烦事。比如密码忘了、人脸识别 / 指纹识别突然不灵,或者买了二手 iPhone 却被原来的 iCloud 账号锁住,这时候就需要靠谱的解锁工具来帮忙了。Aiseesoft iPhone Unlocker 就是专门解决这些问题的软件&…...

UDP(Echoserver)
网络命令 Ping 命令 检测网络是否连通 使用方法: ping -c 次数 网址ping -c 3 www.baidu.comnetstat 命令 netstat 是一个用来查看网络状态的重要工具. 语法:netstat [选项] 功能:查看网络状态 常用选项: n 拒绝显示别名&#…...

对WWDC 2025 Keynote 内容的预测
借助我们以往对苹果公司发展路径的深入研究经验,以及大语言模型的分析能力,我们系统梳理了多年来苹果 WWDC 主题演讲的规律。在 WWDC 2025 即将揭幕之际,我们让 ChatGPT 对今年的 Keynote 内容进行了一个初步预测,聊作存档。等到明…...

基于Docker Compose部署Java微服务项目
一. 创建根项目 根项目(父项目)主要用于依赖管理 一些需要注意的点: 打包方式需要为 pom<modules>里需要注册子模块不要引入maven的打包插件,否则打包时会出问题 <?xml version"1.0" encoding"UTF-8…...

CRMEB 框架中 PHP 上传扩展开发:涵盖本地上传及阿里云 OSS、腾讯云 COS、七牛云
目前已有本地上传、阿里云OSS上传、腾讯云COS上传、七牛云上传扩展 扩展入口文件 文件目录 crmeb\services\upload\Upload.php namespace crmeb\services\upload;use crmeb\basic\BaseManager; use think\facade\Config;/*** Class Upload* package crmeb\services\upload* …...

图表类系列各种样式PPT模版分享
图标图表系列PPT模版,柱状图PPT模版,线状图PPT模版,折线图PPT模版,饼状图PPT模版,雷达图PPT模版,树状图PPT模版 图表类系列各种样式PPT模版分享:图表系列PPT模板https://pan.quark.cn/s/20d40aa…...

CMake控制VS2022项目文件分组
我们可以通过 CMake 控制源文件的组织结构,使它们在 VS 解决方案资源管理器中以“组”(Filter)的形式进行分类展示。 🎯 目标 通过 CMake 脚本将 .cpp、.h 等源文件分组显示在 Visual Studio 2022 的解决方案资源管理器中。 ✅ 支持的方法汇总(共4种) 方法描述是否推荐…...
