算法【混合背包】
混合背包是指多种背包模型的组合与转化。
下面通过题目加深理解。
题目一
测试链接:1742 -- Coins
分析:这道题可以通过硬币的个数将其转化为01背包,完全背包和多重背包。如果硬币的个数是1个,则是01背包;如果硬币的面值×硬币的个数大于当前需要找零的数额,则是完全背包;否则是多重背包。对于不同的背包进行不同的可能性展开,最后统计,即可得到答案。代码如下。
#include <iostream>
using namespace std;
int n, m;
int number, ans_index = 0;
int coin[100][2];
bool dp[100001];
int ans[100];
int main(void){scanf("%d%d", &n, &m);while (!(n == 0 && m == 0)){number = 0;for(int i = 0;i < n;++i){scanf("%d", &coin[i][0]);}for(int i = 0;i < n;++i){scanf("%d", &coin[i][1]);}for(int i = 1;i <= m;++i){dp[i] = false;}dp[0] = true;for(int i = 0;i < n;++i){if(coin[i][1] == 1){for(int j = m;j >= 0 && j - coin[i][0] >= 0;--j){dp[j] |= dp[j-coin[i][0]];}}else if(coin[i][0] * coin[i][1] > m){for(int j = 0;j <= m;++j){if(j - coin[i][0] >= 0){dp[j] |= dp[j-coin[i][0]];}}}else{for(int j = m;j >= 0;--j){for(int k = 1;k <= coin[i][1] && j - k * coin[i][0] >= 0;++k){dp[j] |= dp[j-k*coin[i][0]];}}}}for(int i = 1;i <= m;++i){if(dp[i]){++number;}}ans[ans_index++] = number;scanf("%d%d", &n, &m);}for(int i = 0;i < ans_index;++i){printf("%d\n", ans[i]);}return 0;
}
其中,求dp数组循环中,i为在下标0~i的物品中取。当然,这道题其实可以直接将其当作一个多重背包,二进制优化后转化为01背包进行求解。代码如下。
#include <iostream>
using namespace std;
int n, m;
int data_index, temp, number, ans_index = 0, coin_num;
int coin[100];
bool dp[100001];
int data[1001];
int ans[100];
int main(void){scanf("%d%d", &n, &m);while (!(n == 0 && m == 0)){data_index = 0;number = 0;for(int i = 0;i < n;++i){scanf("%d", &coin[i]);}for(int i = 0;i < n;++i){scanf("%d", &coin_num);temp = 1;while (coin_num >= temp){data[data_index++] = temp * coin[i];coin_num -= temp;temp *= 2;}if(coin_num > 0){data[data_index++] = coin_num * coin[i];}}for(int i = 1;i <= m;++i){dp[i] = false;}dp[0] = true;for(int i = 0;i < data_index;++i){for(int j = m;j >= 0 && j - data[i] >= 0;--j){dp[j] |= dp[j-data[i]];}}for(int i = 1;i <= m;++i){if(dp[i]){++number;}}ans[ans_index++] = number;scanf("%d%d", &n, &m);}for(int i = 0;i < ans_index;++i){printf("%d\n", ans[i]);}return 0;
}
相关文章:

算法【混合背包】
混合背包是指多种背包模型的组合与转化。 下面通过题目加深理解。 题目一 测试链接:1742 -- Coins 分析:这道题可以通过硬币的个数将其转化为01背包,完全背包和多重背包。如果硬币的个数是1个,则是01背包;如果硬币的…...
)
WordPress eventon-lite插件存在未授权信息泄露漏洞(CVE-2024-0235)
免责声明: 本文旨在提供有关特定漏洞的深入信息,帮助用户充分了解潜在的安全风险。发布此信息的目的在于提升网络安全意识和推动技术进步,未经授权访问系统、网络或应用程序,可能会导致法律责任或严重后果。因此,作者不对读者基于本文内容所采取的任何行为承担责任。读者在…...

基于微信小程序的医院预约挂号系统设计与实现(LW+源码+讲解)
专注于大学生项目实战开发,讲解,毕业答疑辅导,欢迎高校老师/同行前辈交流合作✌。 技术范围:SpringBoot、Vue、SSM、HLMT、小程序、Jsp、PHP、Nodejs、Python、爬虫、数据可视化、安卓app、大数据、物联网、机器学习等设计与开发。 主要内容:…...

C++初阶 -- 手撕string类(模拟实现string类)
目录 一、string类的成员变量 二、构造函数 2.1 无参版本 2.2 有参版本 2.3 缺省值版本 三、析构函数 四、拷贝构造函数 五、c_str函数 六、operator重载 七、size函数 八、迭代器iterator 8.1 正常版本 8.2 const版本 九、operator[] 9.1 正常版本 9.2 const版…...

【Postman接口测试】Postman的安装和使用
在软件测试领域,接口测试是保障软件质量的关键环节之一,而Postman作为一款功能强大且广受欢迎的接口测试工具,能够帮助测试人员高效地进行接口测试工作。本文将详细介绍Postman的安装和使用方法,让你快速上手这款工具。 一、Pos…...
miniconda学习笔记
文章主要内容:演示miniconda切换不同python环境,安装python库,使用pycharm配置不同的conda建的python环境 目录 一、miniconda 1. 是什么? 2.安装miniconda 3.基本操作 一、miniconda 1. 是什么? miniconda是一个anac…...

区块链项目孵化与包装设计:从概念到市场的全流程指南
区块链技术的快速发展催生了大量创新项目,但如何将一个区块链项目从概念孵化成市场认可的产品,是许多团队面临的挑战。本文将从孵化策略、包装设计和市场落地三个维度,为你解析区块链项目成功的关键步骤。 一、区块链项目孵化的核心要素 明确…...

JavaScript的基本组成
1、JavaScript的组成部分 JavaScript可以分为三个部分:ECMAScript标准、DOM、BOM。 ECMAScript标准 即JS的基本语法,JavaScript的核心,描述了语言的基本语法和数据类型,ECMAScript是一套标 准,定义了一种语言…...
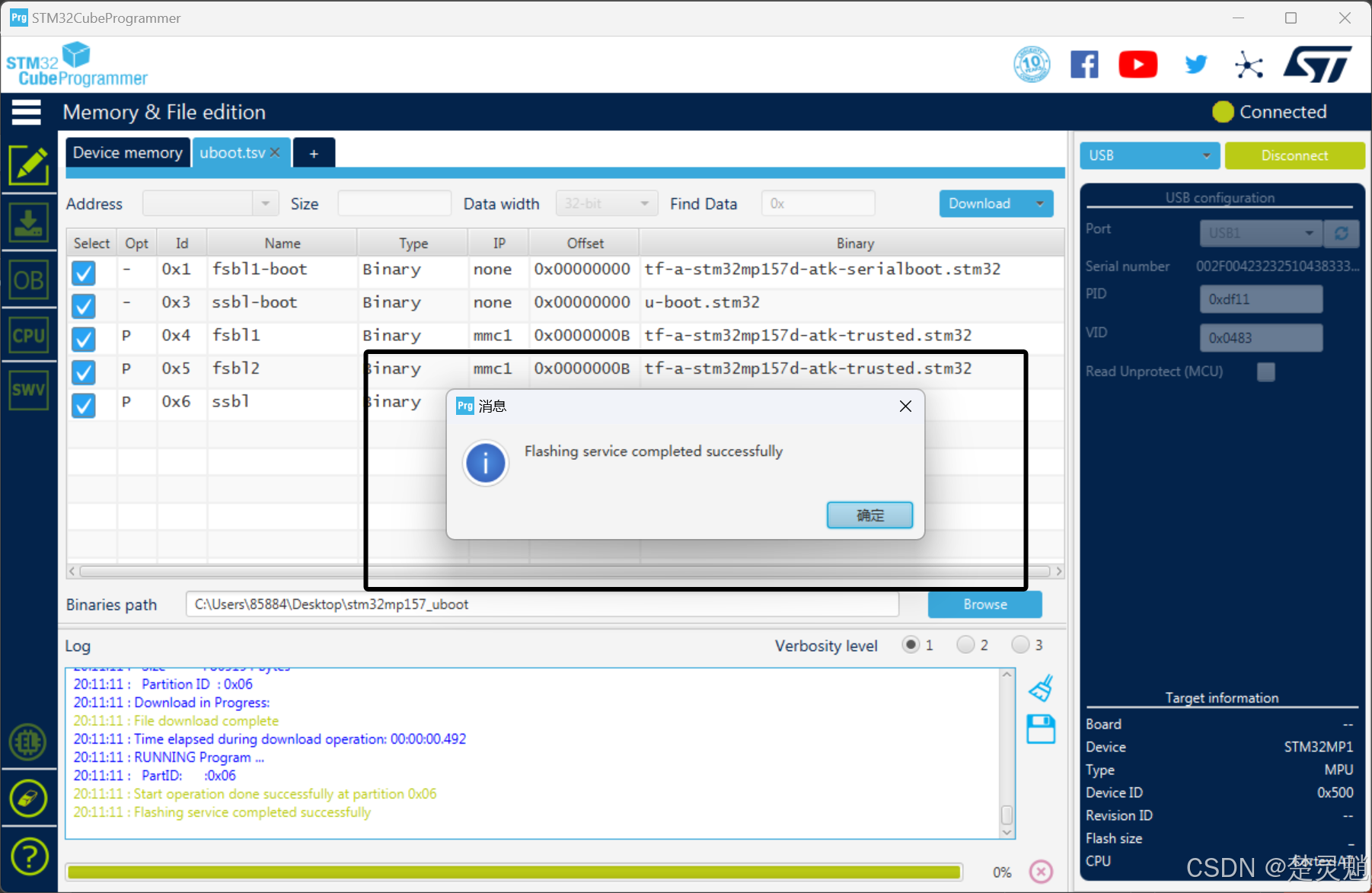
[Linux]从零开始的STM32MP157 U-Boot移植
一、前言 在上一次教程中,我们了解了STM32MP157的启动流程与安全启动机制。我们还将FSBL的相关代码移植成功了。大家还记得FSBL的下一个步骤是什么吗?没错,就是SSBL,而且常见的我们将SSBL作为存放U-Boot的地方。所以本次教程&…...

【Unity3D】实现横版2D游戏——攀爬绳索(简易版)
目录 GeneRope.cs 场景绳索生成类 HeroColliderController.cs 控制角色与单向平台是否忽略碰撞 HeroClampController.cs 控制角色攀爬 OnTriggerEnter2D方法 OnTriggerStay2D方法 OnTriggerExit2D方法 Update方法 开始攀爬 结束攀爬 Sensor_HeroKnight.cs 角色触发器…...

【llm对话系统】大模型 Llama 源码分析之 LoRA 微调
1. 引言 微调 (Fine-tuning) 是将预训练大模型 (LLM) 应用于下游任务的常用方法。然而,直接微调大模型的所有参数通常需要大量的计算资源和内存。LoRA (Low-Rank Adaptation) 是一种高效的微调方法,它通过引入少量可训练参数,固定预训练模型…...

算法随笔_35: 每日温度
上一篇:算法随笔_34: 最后一个单词的长度-CSDN博客 题目描述如下: 给定一个整数数组 temperatures ,表示每天的温度,返回一个数组 answer ,其中 answer[i] 是指对于第 i 天,下一个更高温度出现在几天后。如果气温在这之后都不会升…...

嵌入式硬件篇---CPUGPUTPU
文章目录 第一部分:处理器CPU(中央处理器)1.通用性2.核心数3.缓存4.指令集5.功耗和发热 GPU(图形处理器)1.并行处理2.核心数量3.内存带宽4.专门的应用 TPU(张量处理单元)1.为深度学习定制2.低精…...
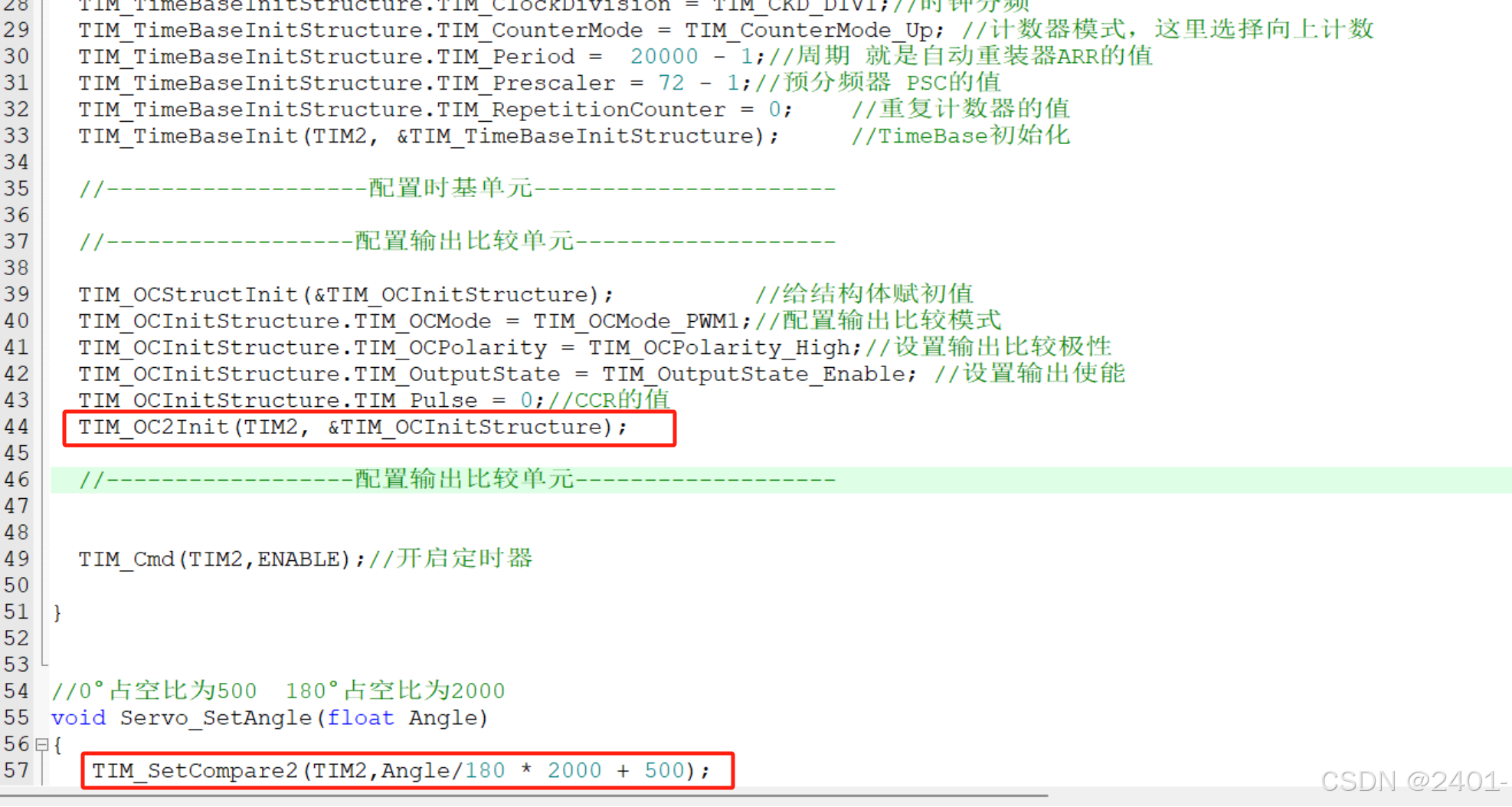
STM32 PWM驱动舵机
接线图: 这里将信号线连接到了开发板的PA1上 代码配置: 这里的PWM配置与呼吸灯一样,呼吸灯连接的是PA0引脚,输出比较单元用的是OC1通道,这里只需改为OC2通道即可。 完整代码: #include "servo.h&quo…...

设计心得——平衡和冗余
一、平衡 在前面分析了一些软件设计的基础和原则后,今天分析一下整体设计上的一些实践问题。首先分析一下设计上的平衡问题。平衡非常好理解,看到过天平或者标称的同学们应该都知道什么平衡。无论在哪个环境里,平衡都是稳定的基础。 既然说到…...

webrtc协议详细解释
### 一、概述与背景 WebRTC(Web Real-Time Communication)最早由 Google 在 2011 年开源,旨在为浏览器与移动端应用提供客户端直连(点对点)方式进行实时音视频及数据传输的能力。传统的网络应用在进行高实时性音视频通…...
动手学强化学习(四)——蒙特卡洛方法
一、蒙特卡洛方法 蒙特卡洛方法是一种无模型(Model-Free)的强化学习算法,它通过直接与环境交互采样轨迹(episodes)来估计状态或动作的价值函数(Value Function),而不需要依赖环境动态…...
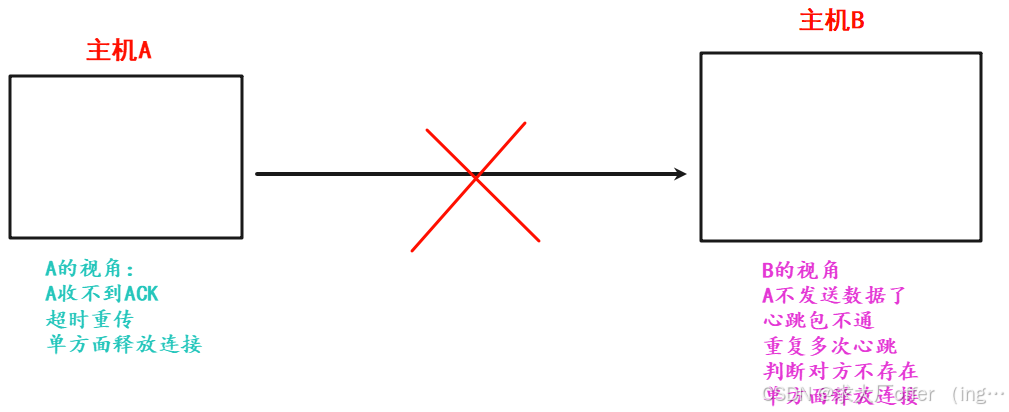
网络原理(3)—— 传输层详解
目录 一. 再谈端口号 二. UDP协议(用户数据报协议) 2.1 UDP协议端格式 2.2 UDP报文长度 2.3 UDP校验和 三. TCP协议(传输控制协议) 3.1 TCP协议段格式 3.2 核心机制 3.2.1 确认应答 —— “感知对方是否收到” 3.2.2 超时重传 3.3.3 连接管理 —— 三次握手与四…...
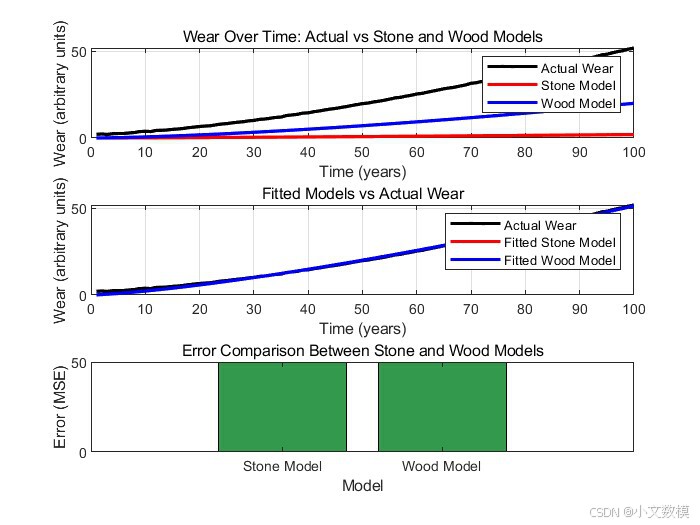
2025美赛美国大学生数学建模竞赛A题完整思路分析论文(43页)(含模型、可运行代码和运行结果)
2025美国大学生数学建模竞赛A题完整思路分析论文 目录 摘要 一、问题重述 二、 问题分析 三、模型假设 四、 模型建立与求解 4.1问题1 4.1.1问题1思路分析 4.1.2问题1模型建立 4.1.3问题1样例代码(仅供参考) 4.1.4问题1样例代码运行结果&…...
Elasticsearch的开发工具(Dev Tools)
目录 说明1. **Console**2. **Search Profiler**3. **Grok Debugger**4. **Painless Lab**总结 说明 Elasticsearch的开发工具(Dev Tools)在Kibana中提供了多种功能强大的工具,用于调试、优化和测试Elasticsearch查询和脚本。以下是关于Cons…...

AI Agent与Agentic AI:原理、应用、挑战与未来展望
文章目录 一、引言二、AI Agent与Agentic AI的兴起2.1 技术契机与生态成熟2.2 Agent的定义与特征2.3 Agent的发展历程 三、AI Agent的核心技术栈解密3.1 感知模块代码示例:使用Python和OpenCV进行图像识别 3.2 认知与决策模块代码示例:使用OpenAI GPT-3进…...

MFC内存泄露
1、泄露代码示例 void X::SetApplicationBtn() {CMFCRibbonApplicationButton* pBtn GetApplicationButton();// 获取 Ribbon Bar 指针// 创建自定义按钮CCustomRibbonAppButton* pCustomButton new CCustomRibbonAppButton();pCustomButton->SetImage(IDB_BITMAP_Jdp26)…...

前端导出带有合并单元格的列表
// 导出async function exportExcel(fileName "共识调整.xlsx") {// 所有数据const exportData await getAllMainData();// 表头内容let fitstTitleList [];const secondTitleList [];allColumns.value.forEach(column > {if (!column.children) {fitstTitleL…...

【Zephyr 系列 10】实战项目:打造一个蓝牙传感器终端 + 网关系统(完整架构与全栈实现)
🧠关键词:Zephyr、BLE、终端、网关、广播、连接、传感器、数据采集、低功耗、系统集成 📌目标读者:希望基于 Zephyr 构建 BLE 系统架构、实现终端与网关协作、具备产品交付能力的开发者 📊篇幅字数:约 5200 字 ✨ 项目总览 在物联网实际项目中,**“终端 + 网关”**是…...

Unit 1 深度强化学习简介
Deep RL Course ——Unit 1 Introduction 从理论和实践层面深入学习深度强化学习。学会使用知名的深度强化学习库,例如 Stable Baselines3、RL Baselines3 Zoo、Sample Factory 和 CleanRL。在独特的环境中训练智能体,比如 SnowballFight、Huggy the Do…...

短视频矩阵系统文案创作功能开发实践,定制化开发
在短视频行业迅猛发展的当下,企业和个人创作者为了扩大影响力、提升传播效果,纷纷采用短视频矩阵运营策略,同时管理多个平台、多个账号的内容发布。然而,频繁的文案创作需求让运营者疲于应对,如何高效产出高质量文案成…...

Linux 下 DMA 内存映射浅析
序 系统 I/O 设备驱动程序通常调用其特定子系统的接口为 DMA 分配内存,但最终会调到 DMA 子系统的dma_alloc_coherent()/dma_alloc_attrs() 等接口。 关于 dma_alloc_coherent 接口详细的代码讲解、调用流程,可以参考这篇文章,我觉得写的非常…...

TCP/IP 网络编程 | 服务端 客户端的封装
设计模式 文章目录 设计模式一、socket.h 接口(interface)二、socket.cpp 实现(implementation)三、server.cpp 使用封装(main 函数)四、client.cpp 使用封装(main 函数)五、退出方法…...

Axure Rp 11 安装、汉化、授权
Axure Rp 11 安装、汉化、授权 1、前言2、汉化2.1、汉化文件下载2.2、windows汉化流程2.3、 macOs汉化流程 3、授权 1、前言 Axure Rp 11官方下载链接:https://www.axure.com/downloadthanks 2、汉化 2.1、汉化文件下载 链接: https://pan.baidu.com/s/18Clf…...

设计模式-3 行为型模式
一、观察者模式 1、定义 定义对象之间的一对多的依赖关系,这样当一个对象改变状态时,它的所有依赖项都会自动得到通知和更新。 描述复杂的流程控制 描述多个类或者对象之间怎样互相协作共同完成单个对象都无法单独度完成的任务 它涉及算法与对象间职责…...
