动手学强化学习(四)——蒙特卡洛方法
一、蒙特卡洛方法
蒙特卡洛方法是一种无模型(Model-Free)的强化学习算法,它通过直接与环境交互采样轨迹(episodes)来估计状态或动作的价值函数(Value Function),而不需要依赖环境动态模型(如转移概率矩阵 P(s′∣s,a)和奖励函数 R(s,a)的显式知识)。简单来说,我们前面来说的策略都是通过公式推导出公式q,但是蒙特卡洛可以直接通过数据量来推出q,这样就省略勒模型
假设,有一枚硬币,抛硬币后,若正面朝上,定义随机变量X=1;若反面朝上X=-1,。目标是计算X的期望E(X)。
基于Model-base的方法,基于已知的概率模型,概率都为0.5,那么期望计算公式E(X)=0.5*1+0.5*(-1)=0
如果通过蒙特卡洛方法,就直接从数据入手。通过多次独立地抛硬币进行采样。比如,抛次硬币,假设得到6次正面,4次反面,对应的值分别为1和-1,计算这次采样的平均值为(6-4)/10 = 0.2,用这个平均数来近似期望。当抛硬币的次数逐渐增大时,根据大数定律,样本均值会越来越趋近于随机变量的期望值。
二、 MC Basic
MC Basic 是蒙特卡洛方法的一种简单实现,结合了策略评估(Policy Evaluation)和策略改进(Policy Improvement)的迭代过程,属于基于策略迭代(Policy Iteration)的无模型算法。在强化学习中,要计算在策略pi下的状态 - 动作值函数 q(s,a),即从状态出发,采取动作a后,遵循策略pi所获得的期望回报。
从状态s出发,采取动作a,然后按照策略pi在环境中进行交互,直到到达终止状态,这一过程称为一个 episode,得到一个回报 g(s,a)。重复上述过程多次,得到多个回报,对这些回报取平均值
随着采样次数的增加,该估计会越来越接近真实的。
2.1 网格世界的蒙特卡洛
在一个M * N 的网格世界中,智能体需要从一个位置移动到另一个位置。每个网格可能有不同的奖励值,例如,有些网格代表正奖励,有些代表负奖励,还有些可能是障碍。智能体要学习一个策略,以最大化从起始状态到终止状态的累积奖励。
智能体从初始状态 s0 开始,按照当前策略选择动作进行移动。假设在某一时刻智能体处于状态,根据策略选择动作,然后转移到下一个状态,并获得奖励。重复这个过程,直到到达终止状态,形成一个 episode,如(s0,a0,r0,s1,a1,r1,...,st,at,r),其中T是终止时刻,该 episode 的回报
2.2 首次访问法
对于每个状态 - 动作对(s,a),只考虑在一个 episode 中第一次访问到(s,a)时后续所获得的回报来估计qpi(s,a)。例如,在一个 episode 中多次访问到(s,a),但只使用第一次访问后得到的回报 G 来更新对qpi(s,a)的估计。若有n个 episode 中首次访问到(s,a),得到的回报分别为G1,G2,G3...,则的估计值为。
2.3 每次访问法
对于每个状态 - 动作对(s,a),在一个 episode 中每次访问到(s,a)时后续所获得的回报都用于估计qpi(s,a)。即每次访问到(s,a)都记录下后续的回报,然后对所有这些回报求平均值来更新qpi(s,a)的估计。
同样使用贪心策略来迭代到最终
相关文章:
动手学强化学习(四)——蒙特卡洛方法
一、蒙特卡洛方法 蒙特卡洛方法是一种无模型(Model-Free)的强化学习算法,它通过直接与环境交互采样轨迹(episodes)来估计状态或动作的价值函数(Value Function),而不需要依赖环境动态…...
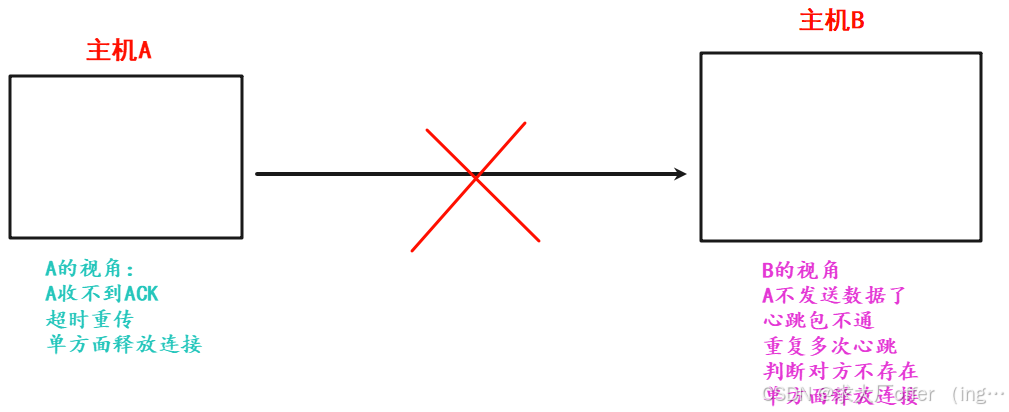
网络原理(3)—— 传输层详解
目录 一. 再谈端口号 二. UDP协议(用户数据报协议) 2.1 UDP协议端格式 2.2 UDP报文长度 2.3 UDP校验和 三. TCP协议(传输控制协议) 3.1 TCP协议段格式 3.2 核心机制 3.2.1 确认应答 —— “感知对方是否收到” 3.2.2 超时重传 3.3.3 连接管理 —— 三次握手与四…...
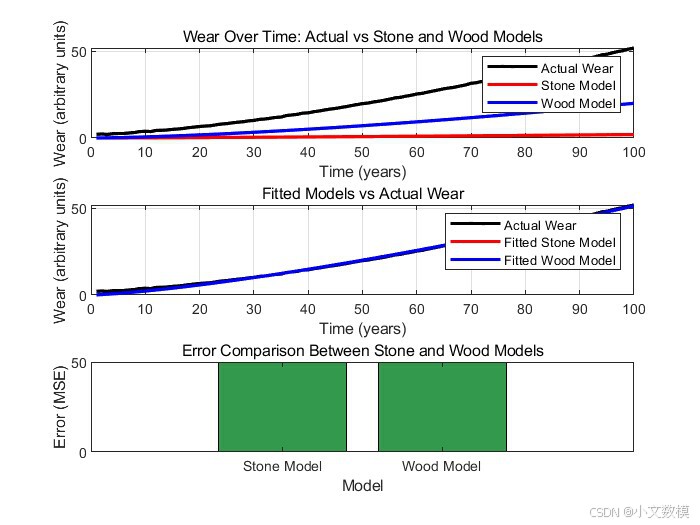
2025美赛美国大学生数学建模竞赛A题完整思路分析论文(43页)(含模型、可运行代码和运行结果)
2025美国大学生数学建模竞赛A题完整思路分析论文 目录 摘要 一、问题重述 二、 问题分析 三、模型假设 四、 模型建立与求解 4.1问题1 4.1.1问题1思路分析 4.1.2问题1模型建立 4.1.3问题1样例代码(仅供参考) 4.1.4问题1样例代码运行结果&…...
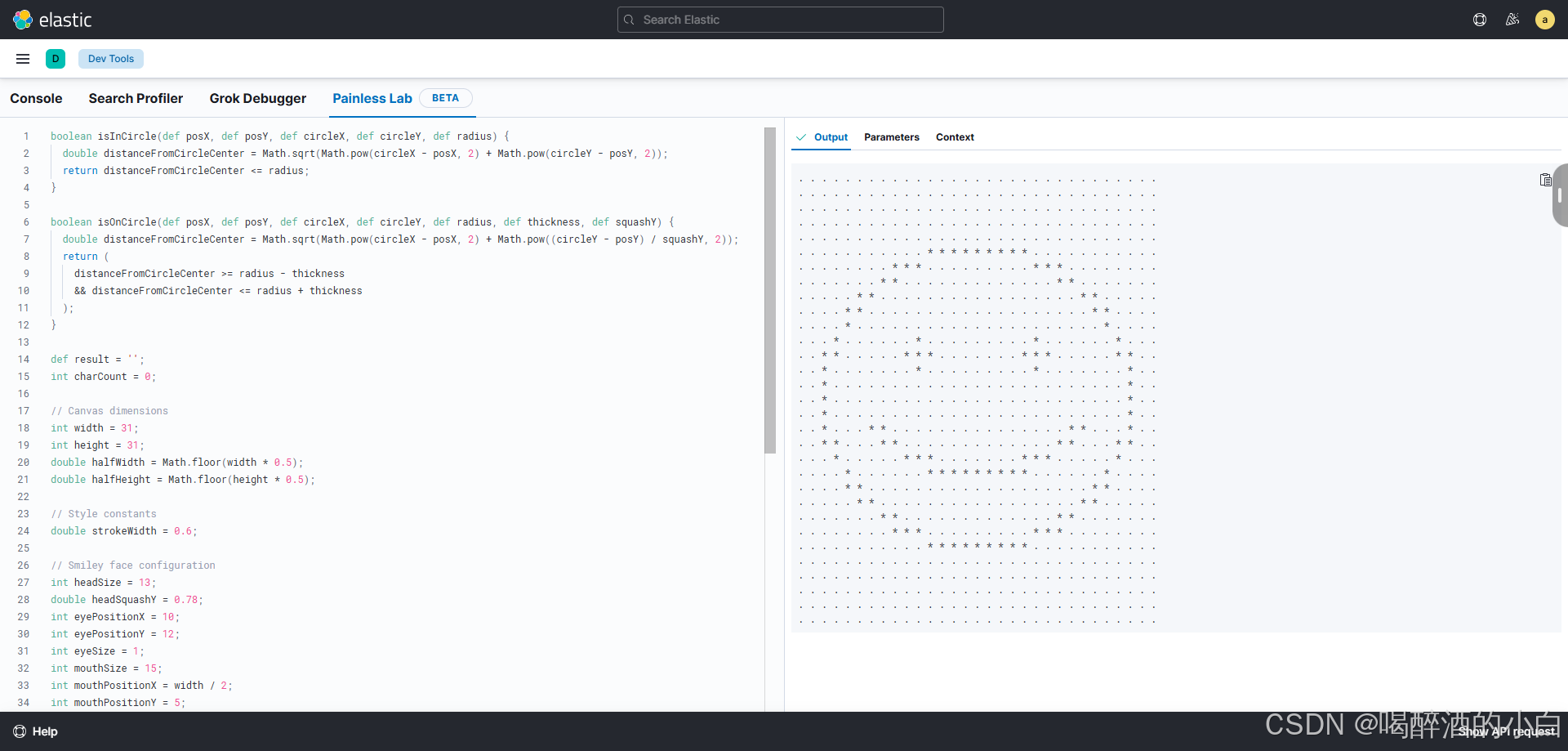
Elasticsearch的开发工具(Dev Tools)
目录 说明1. **Console**2. **Search Profiler**3. **Grok Debugger**4. **Painless Lab**总结 说明 Elasticsearch的开发工具(Dev Tools)在Kibana中提供了多种功能强大的工具,用于调试、优化和测试Elasticsearch查询和脚本。以下是关于Cons…...

Python-基于PyQt5,pdf2docx,pathlib的PDF转Word工具
前言:日常生活中,我们常常会跟WPS Office打交道。作表格,写报告,写PPT......可以说,我们的生活已经离不开WPS Office了。与此同时,我们在这个过程中也会遇到各种各样的技术阻碍,例如部分软件的PDF转Word需要收取额外费用等。那么,可不可以自己开发一个小工具来实现PDF转…...
小程序-视图与逻辑
前言 1. 声明式导航 open-type"switchTab"如果没有写这个,因为是tabBar所以写这个,就无法跳转。路径开始也必须为斜线 open-type"navigate"这个可以不写 现在开始实现后退的效果 现在我们就在list页面里面实现后退 2.编程式导航…...
UE5制作视差图
双目深度估计开源数据集很多都是用UE制作的,那么我们自己能否通过UE制作自己想要的场景的数据集呢。最近花了点时间研究了一下,分享给需要的小伙伴。 主要使用的是UnrealCV插件,UnrealCV是一个开源项目,旨在帮助计算机视觉研究人…...

海浪波高预测(背景调研)
#新星杯14天创作挑战营第7期# ps:图片由通义千问生成 历史工作: 针对更高细粒度、更高精度的波浪高度预测任务: Mumtaz Ali 等人提出了一种多元线性回归模型(MLR-CWLS),该模型利用协方差加权最小二乘法&a…...

代码随想录算法训练营第四十二天-动态规划-股票-188.买卖股票的最佳时机IV
题目要求进行k次买卖其实就是上一题的扩展,把2次扩展为k次定义动规数组依然是二维,第一个维度表示第几天,第二个维度表示第几次买入和卖出所以第二个维度的长度应该是2k1在for循环内,要使用一个内循环来表示第几次买入或卖出&…...
Gradle配置指南:深入解析settings.gradle.kts(Kotlin DSL版)
文章目录 Gradle配置指南:深入解析settings.gradle.kts(Kotlin DSL版)settings.gradle.kts 基础配置选项单项目配置多项目配置 高级配置选项插件管理(Plugin Management)基础配置模板案例:Android项目标准配…...
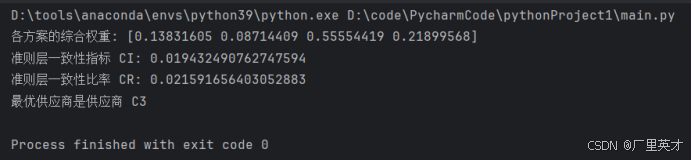
软件工程经济学-日常作业+大作业
目录 一、作业1 作业内容 解答 二、作业2 作业内容 解答 三、作业3 作业内容 解答 四、大作业 作业内容 解答 1.建立层次结构模型 (1)目标层 (2)准则层 (3)方案层 2.构造判断矩阵 (1)准则层判断矩阵 (2)方案层判断矩阵 3.层次单排序及其一致性检验 代码 …...
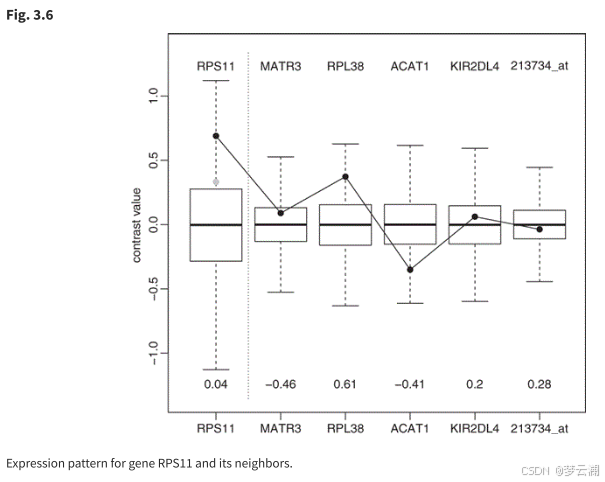
论文阅读(三):微阵列数据的图形模型和多变量分析
1.论文链接:Graphical Models and Multivariate Analysis of Microarray Data 摘要: 基因表达数据的通常分析忽略了基因表达值之间的相关性。从生物学上讲,这种假设是不合理的。本章介绍的方法允许通过稀疏高斯图形模型来描述基因之间的相关…...
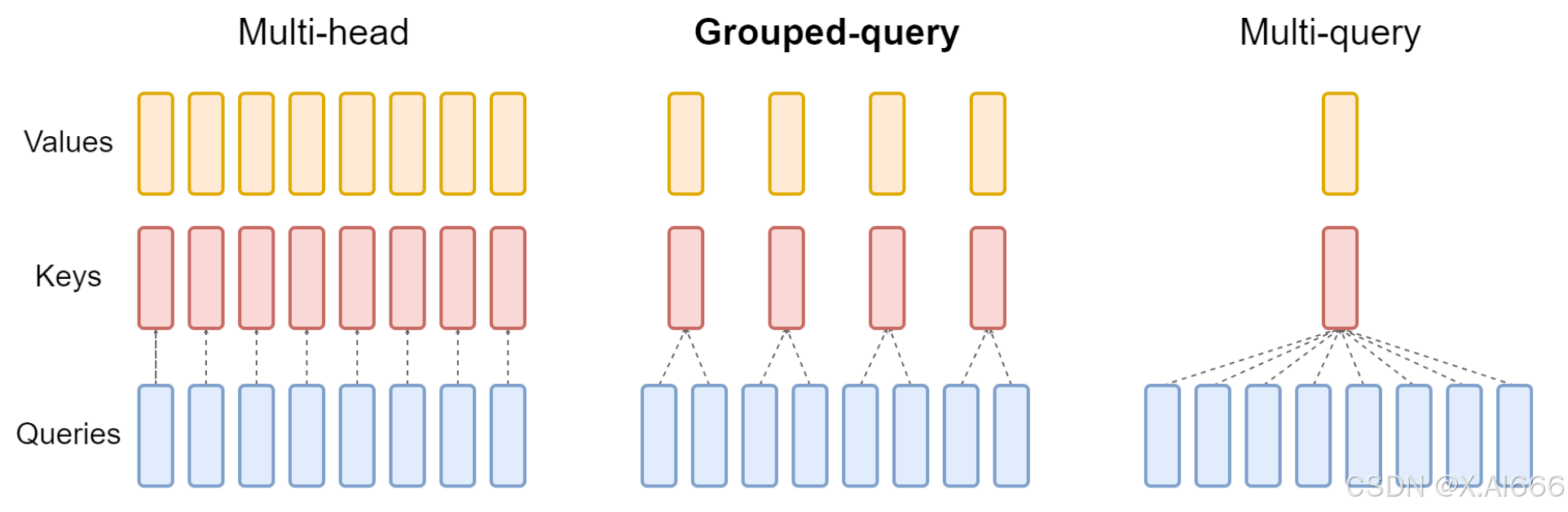
【大模型LLM面试合集】大语言模型架构_MHA_MQA_GQA
MHA_MQA_GQA 1.总结 在 MHA(Multi Head Attention) 中,每个头有自己单独的 key-value 对;标准的多头注意力机制,h个Query、Key 和 Value 矩阵。在 MQA(Multi Query Attention) 中只会有一组 k…...
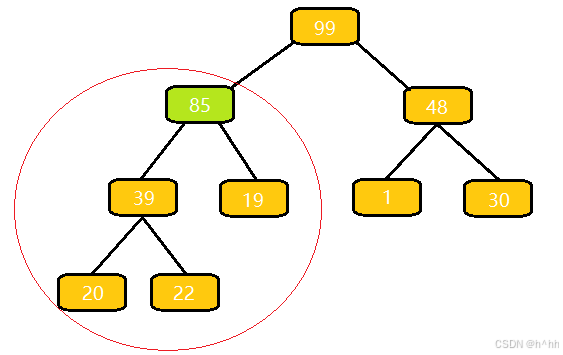
向上调整算法(详解)c++
算法流程: 与⽗结点的权值作⽐较,如果⽐它⼤,就与⽗亲交换; 交换完之后,重复 1 操作,直到⽐⽗亲⼩,或者换到根节点的位置 这里为什么插入85完后合法? 我们插入一个85,…...
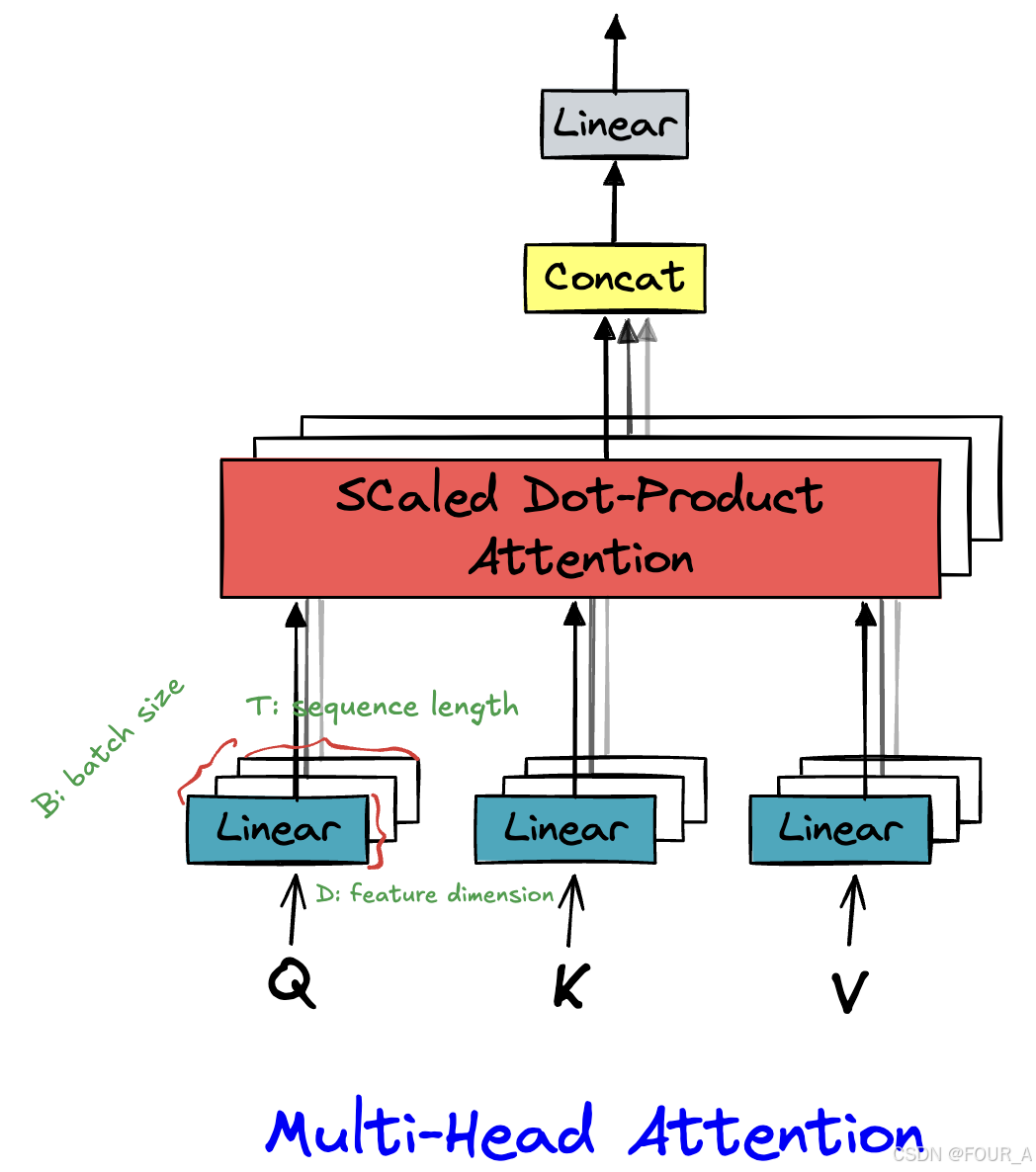
【Transformer】手撕Attention
import torch from torch import nn import torch.functional as F import mathX torch.randn(16,64,512) # B,T,Dd_model 512 # 模型的维度 n_head 8 # 注意力头的数量多头注意力机制 class multi_head_attention(nn.Module): def __init__(self, d_model, n_hea…...

844.比较含退格的字符串
目录 题目思路解法收获 题目 给定 s 和 t 两个字符串,当它们分别被输入到空白的文本编辑器后,如果两者相等,返回 true 。# 代表退格字符。 注意:如果对空文本输入退格字符,文本继续为空。 思路 如何解退格之后left…...

图书管理系统 Axios 源码__编辑图书
目录 功能概述: 代码实现(index.js): 代码解析: 图书管理系统中,删除图书功能是核心操作之一。下是基于 HTML、Bootstrap、JavaScript 和 Axios 实现的删除图书功能的详细介绍。 功能概述: …...
LabVIEW纤维集合体微电流测试仪
LabVIEW开发纤维集合体微电流测试仪。该设备精确测量纤维材料在特定电压下的电流变化,以分析纤维的结构、老化及回潮率等属性,对于纤维材料的科学研究及质量控制具有重要意义。 项目背景 在纤维材料的研究与应用中,电学性能是评估其性能…...

Commander 一款命令行自定义命令依赖
一、安装 commander 插件 npm install commander 二、基本用法 1. 创建一个简单的命令行程序 创建一个 JavaScript 文件,例如 mycli.js,并添加以下代码: // 引入 commander 模块并获取 program 对象。const { program } require("…...
)
Day24 洛谷普及2004(内涵前缀和与差分算法)
零基础洛谷刷题记录 Day01 2024.11.18 Day02 2024.11.25 Day03 2024.11.26 Day04 2024.11.28 Day05 2024.11.29 Day06 2024 12.02 Day07 2024.12.03 Day08 2024 12 05 Day09 2024.12.07 Day10 2024.12.09 Day11 2024.12.10 Day12 2024.12.12 Day13 2024.12.16 Day14 2024.12.1…...

日语AI面试高效通关秘籍:专业解读与青柚面试智能助攻
在如今就业市场竞争日益激烈的背景下,越来越多的求职者将目光投向了日本及中日双语岗位。但是,一场日语面试往往让许多人感到步履维艰。你是否也曾因为面试官抛出的“刁钻问题”而心生畏惧?面对生疏的日语交流环境,即便提前恶补了…...

令牌桶 滑动窗口->限流 分布式信号量->限并发的原理 lua脚本分析介绍
文章目录 前言限流限制并发的实际理解限流令牌桶代码实现结果分析令牌桶lua的模拟实现原理总结: 滑动窗口代码实现结果分析lua脚本原理解析 限并发分布式信号量代码实现结果分析lua脚本实现原理 双注解去实现限流 并发结果分析: 实际业务去理解体会统一注…...

C# 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

初学 pytest 记录
安装 pip install pytest用例可以是函数也可以是类中的方法 def test_func():print()class TestAdd: # def __init__(self): 在 pytest 中不可以使用__init__方法 # self.cc 12345 pytest.mark.api def test_str(self):res add(1, 2)assert res 12def test_int(self):r…...

在Ubuntu24上采用Wine打开SourceInsight
1. 安装wine sudo apt install wine 2. 安装32位库支持,SourceInsight是32位程序 sudo dpkg --add-architecture i386 sudo apt update sudo apt install wine32:i386 3. 验证安装 wine --version 4. 安装必要的字体和库(解决显示问题) sudo apt install fonts-wqy…...

AirSim/Cosys-AirSim 游戏开发(四)外部固定位置监控相机
这个博客介绍了如何通过 settings.json 文件添加一个无人机外的 固定位置监控相机,因为在使用过程中发现 Airsim 对外部监控相机的描述模糊,而 Cosys-Airsim 在官方文档中没有提供外部监控相机设置,最后在源码示例中找到了,所以感…...
提供了哪些便利?)
现有的 Redis 分布式锁库(如 Redisson)提供了哪些便利?
现有的 Redis 分布式锁库(如 Redisson)相比于开发者自己基于 Redis 命令(如 SETNX, EXPIRE, DEL)手动实现分布式锁,提供了巨大的便利性和健壮性。主要体现在以下几个方面: 原子性保证 (Atomicity)ÿ…...

vulnyx Blogger writeup
信息收集 arp-scan nmap 获取userFlag 上web看看 一个默认的页面,gobuster扫一下目录 可以看到扫出的目录中得到了一个有价值的目录/wordpress,说明目标所使用的cms是wordpress,访问http://192.168.43.213/wordpress/然后查看源码能看到 这…...

Bean 作用域有哪些?如何答出技术深度?
导语: Spring 面试绕不开 Bean 的作用域问题,这是面试官考察候选人对 Spring 框架理解深度的常见方式。本文将围绕“Spring 中的 Bean 作用域”展开,结合典型面试题及实战场景,帮你厘清重点,打破模板式回答,…...

嵌入式学习之系统编程(九)OSI模型、TCP/IP模型、UDP协议网络相关编程(6.3)
目录 一、网络编程--OSI模型 二、网络编程--TCP/IP模型 三、网络接口 四、UDP网络相关编程及主要函数 编辑编辑 UDP的特征 socke函数 bind函数 recvfrom函数(接收函数) sendto函数(发送函数) 五、网络编程之 UDP 用…...
