软件工程经济学-日常作业+大作业
目录
一、作业1
作业内容
解答
二、作业2
作业内容
解答
三、作业3
作业内容
解答
四、大作业
作业内容
解答
1.建立层次结构模型
(1)目标层
(2)准则层
(3)方案层
2.构造判断矩阵
(1)准则层判断矩阵
(2)方案层判断矩阵
3.层次单排序及其一致性检验
代码
运行结果
4.层次总排序及其一致性检验
代码
运行结果
决策
一、作业1
作业内容
练习题1:请根据下表绘制相应的网络计划图

解答

二、作业2
作业内容
练习题2:请根据下表绘制相应的网络计划图

解答

三、作业3
作业内容
作业3:某软件工程项目经工作分解后,给出了活动明细表,如下表所示:
1、求解每个活动的te值,并填入表中;
2、绘制对应计划网络图;
3、求解该计划网络图的关键活动、关键节点和关键路线。

解答
1、求解每个活动的te值,并填入表中
| 编号 | 活动代号 | t0 | tm | tp | te | 紧前活动 |
| 1 | A | 6 | 7.5 | 12 | 8 | - |
| 2 | B | 4.5 | 4.8 | 6.3 | 5 | A |
| 3 | C | 1.2 | 2 | 2.8 | 2 | A |
| 4 | D | 5 | 6.7 | 10.2 | 7 | A |
| 5 | E | 4.6 | 5.7 | 8.6 | 6 | B |
| 6 | F | 5.5 | 6 | 6.5 | 6 | C |
| 7 | G | 0 | 0 | 0 | 0 | B |
| 8 | H | 5.5 | 7 | 8.5 | 7 | F、G |
| 9 | I | 3.5 | 5.2 | 5.7 | 5 | H |
| 10 | J | 4.7 | 5.9 | 7.7 | 6 | D、E、I |
2、绘制对应计划网络图

3、求解该计划网络图的关键活动、关键节点和关键路线
关键活动:A、C、F、H、I、J
关键节点:1、2、3、5、6、7、8
关键路线:A->C->F->H->I->J
四、大作业
作业内容
要求:某企业计划采购一批生产设备,现有四家供应商提供的设备备选。请运用层次分析法,从设备的功能性、价格、外观、售后服务等多个方面(可添加考虑因素,自由发挥)进行综合评价,选出最优的供应商。
解答
1.建立层次结构模型
(1)目标层
选择最优的生产设备供应商
(2)准则层
功能性(B1)
价格(B2)
外观(B3)
售后服务(B4)
(3)方案层
供应商C1
供应商C2
供应商C3
供应商C4
2.构造判断矩阵
(1)准则层判断矩阵
为了建立准则层的判断矩阵,我们对各个准则进行成对比较,判断它们在选择供应商时的重要性。我们使用1-9标度法进行比较(1表示两者同等重要,9表示一个因素比另一个重要9倍,反之使用倒数)。
| 功能性 (B1) | 价格 (B2) | 外观 (B3) | 售后服务 (B4) | |
| 功能性 (B1) | 1 | 5 | 3 | 7 |
| 价格 (B2) | 1/5 | 1 | 1/3 | 2 |
| 外观 (B3) | 1/3 | 3 | 1 | 4 |
| 售后服务 (B4) | 1/7 | 1/2 | 1/4 | 1 |
(2)方案层判断矩阵
接下来,我们对每个准则下的供应商进行成对比较。以下为供应商在功能性(B1)、价格(B2)、外观(B3)和售后服务(B4)方面的判断矩阵。我们同样采用1-9标度法进行比较。
供应商在功能性(B1)方面的判断矩阵:
| C1 | C2 | C3 | C4 | |
| C1 | 1 | 3 | 1/5 | 2 |
| C2 | 1/3 | 1 | 1/7 | 1/3 |
| C3 | 5 | 7 | 1 | 9 |
| C4 | 1/2 | 3 | 1/9 | 1 |
供应商在价格(B2)方面的判断矩阵:
| C1 | C2 | C3 | C4 | |
| C1 | 1 | 1/3 | 5 | 1/7 |
| C2 | 3 | 1 | 7 | 1/3 |
| C3 | 1/5 | 1/7 | 1 | 1/9 |
| C4 | 7 | 3 | 9 | 1 |
供应商在外观(B3)方面的判断矩阵:
| C1 | C2 | C3 | C4 | |
| C1 | 1 | 1/2 | 3 | 1/5 |
| C2 | 2 | 1 | 5 | 1/3 |
| C3 | 1/3 | 1/5 | 1 | 1/7 |
| C4 | 5 | 3 | 7 | 1 |
供应商在售后服务(B4)方面的判断矩阵:
| C1 | C2 | C3 | C4 | |
| C1 | 1 | 5 | 1/3 | 2 |
| C2 | 1/5 | 1 | 1/7 | 1/3 |
| C3 | 3 | 7 | 1 | 5 |
| C4 | 1/2 | 3 | 1/5 | 1 |
3.层次单排序及其一致性检验
代码
import numpy as np# 计算特征向量和最大特征值def calculate_eigenvector(matrix):# 计算矩阵的特征值和特征向量eigvals, eigvecs = np.linalg.eig(matrix)# 选择最大特征值的索引max_eigval_index = np.argmax(eigvals)max_eigval = eigvals[max_eigval_index]# 归一化特征向量eigvec = eigvecs[:, max_eigval_index]eigvec = eigvec / np.sum(eigvec) # 归一化,使其和为1return eigvec.real, max_eigval.real# 一致性检验def consistency_check(matrix, max_eigval):n = matrix.shape[0] # 矩阵的维度CI = (max_eigval - n) / (n - 1) # 一致性指标 CIRI = [0, 0, 0.58, 0.9, 1.12, 1.24, 1.32, 1.41, 1.45] # 随机一致性指标 RI(根据矩阵维度n)CR = CI / RI[n - 1] # 一致性比率 CRreturn CI, CR# 示例:准则层判断矩阵B1_matrix = np.array([[1, 5, 3, 7],[1 / 5, 1, 1 / 3, 2],[1 / 3, 3, 1, 4],[1 / 7, 1 / 2, 1 / 4, 1]])# 计算特征向量和最大特征值eigvec_B1, max_eigval_B1 = calculate_eigenvector(B1_matrix)# 输出特征向量和最大特征值print("准则层特征向量:", eigvec_B1)print("准则层最大特征值:", max_eigval_B1)# 一致性检验CI_B1, CR_B1 = consistency_check(B1_matrix, max_eigval_B1)# 输出一致性检验结果print("准则层一致性指标 CI:", CI_B1)print("准则层一致性比率 CR:", CR_B1)# 判断一致性if CR_B1 < 0.1:print("准则层判断矩阵一致性通过")else:print("准则层判断矩阵一致性不通过,需要重新构造判断矩阵")运行结果

4.层次总排序及其一致性检验
代码
import numpy as np# 计算特征向量和最大特征值def calculate_eigenvector(matrix):eigvals, eigvecs = np.linalg.eig(matrix)max_eigval_index = np.argmax(eigvals)max_eigval = eigvals[max_eigval_index]eigvec = eigvecs[:, max_eigval_index]eigvec = eigvec / np.sum(eigvec) # 归一化,使其和为1return eigvec.real, max_eigval.real# 一致性检验def consistency_check(matrix, max_eigval):n = matrix.shape[0] # 矩阵的维度CI = (max_eigval - n) / (n - 1) # 一致性指标 CIRI = [0, 0, 0.58, 0.9, 1.12, 1.24, 1.32, 1.41, 1.45] # 随机一致性指标 RI(根据矩阵维度n)CR = CI / RI[n - 1] # 一致性比率 CRreturn CI, CR# 计算层次总排序def calculate_total_ranking(criteria_weights, matrix_list):# matrix_list 是方案层的判断矩阵列表rankings = []for i, matrix in enumerate(matrix_list):eigvec, max_eigval = calculate_eigenvector(matrix)CI, CR = consistency_check(matrix, max_eigval)# 计算每个方案在该准则下的权重weight = np.dot(eigvec, criteria_weights[i])rankings.append(weight)# 综合排序,得到每个方案的总权重total_weights = np.sum(rankings, axis=0)return total_weights# 示例:准则层判断矩阵B1_matrix = np.array([[1, 5, 3, 7],[1 / 5, 1, 1 / 3, 2],[1 / 3, 3, 1, 4],[1 / 7, 1 / 2, 1 / 4, 1]])# 示例:方案层判断矩阵C1_matrix = np.array([[1, 3, 1 / 5, 2],[1 / 3, 1, 1 / 7, 1 / 3],[5, 7, 1, 9],[1 / 2, 3, 1 / 9, 1]])C2_matrix = np.array([[1, 1 / 3, 5, 1 / 7],[3, 1, 7, 1 / 3],[1 / 5, 1 / 7, 1, 1 / 9],[7, 3, 9, 1]])C3_matrix = np.array([[1, 2, 1 / 3, 1 / 5],[1 / 2, 1, 1 / 9, 1 / 7],[3, 9, 1, 7],[5, 7, 1 / 7, 1]])C4_matrix = np.array([[1, 1 / 2, 3, 1 / 4],[2, 1, 5, 1 / 3],[1 / 3, 1 / 5, 1, 1 / 7],[4, 3, 7, 1]])# 计算准则层的权重(特征向量)criteria_matrix = B1_matrix # 假设准则层只有一个判断矩阵criteria_weights, max_eigval_B1 = calculate_eigenvector(criteria_matrix)# 计算方案层的综合权重matrix_list = [C1_matrix, C2_matrix, C3_matrix, C4_matrix] # 方案层判断矩阵列表total_weights = calculate_total_ranking(criteria_weights, matrix_list)# 输出层次总排序print("各方案的综合权重:", total_weights)# 判断是否一致CI_B1, CR_B1 = consistency_check(criteria_matrix, max_eigval_B1)print("准则层一致性指标 CI:", CI_B1)print("准则层一致性比率 CR:", CR_B1)# 根据综合权重选择最优方案best_supplier_index = np.argmax(total_weights)print(f"最优供应商是供应商 C{best_supplier_index + 1}")运行结果
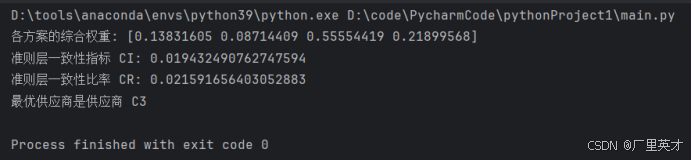
决策
最优供应商为C3
相关文章:

软件工程经济学-日常作业+大作业
目录 一、作业1 作业内容 解答 二、作业2 作业内容 解答 三、作业3 作业内容 解答 四、大作业 作业内容 解答 1.建立层次结构模型 (1)目标层 (2)准则层 (3)方案层 2.构造判断矩阵 (1)准则层判断矩阵 (2)方案层判断矩阵 3.层次单排序及其一致性检验 代码 …...
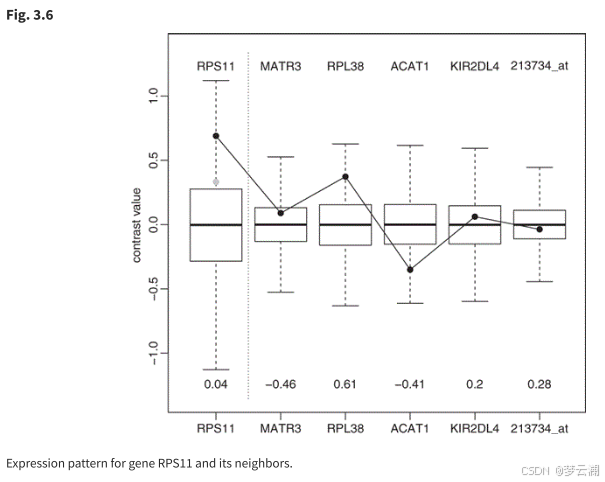
论文阅读(三):微阵列数据的图形模型和多变量分析
1.论文链接:Graphical Models and Multivariate Analysis of Microarray Data 摘要: 基因表达数据的通常分析忽略了基因表达值之间的相关性。从生物学上讲,这种假设是不合理的。本章介绍的方法允许通过稀疏高斯图形模型来描述基因之间的相关…...
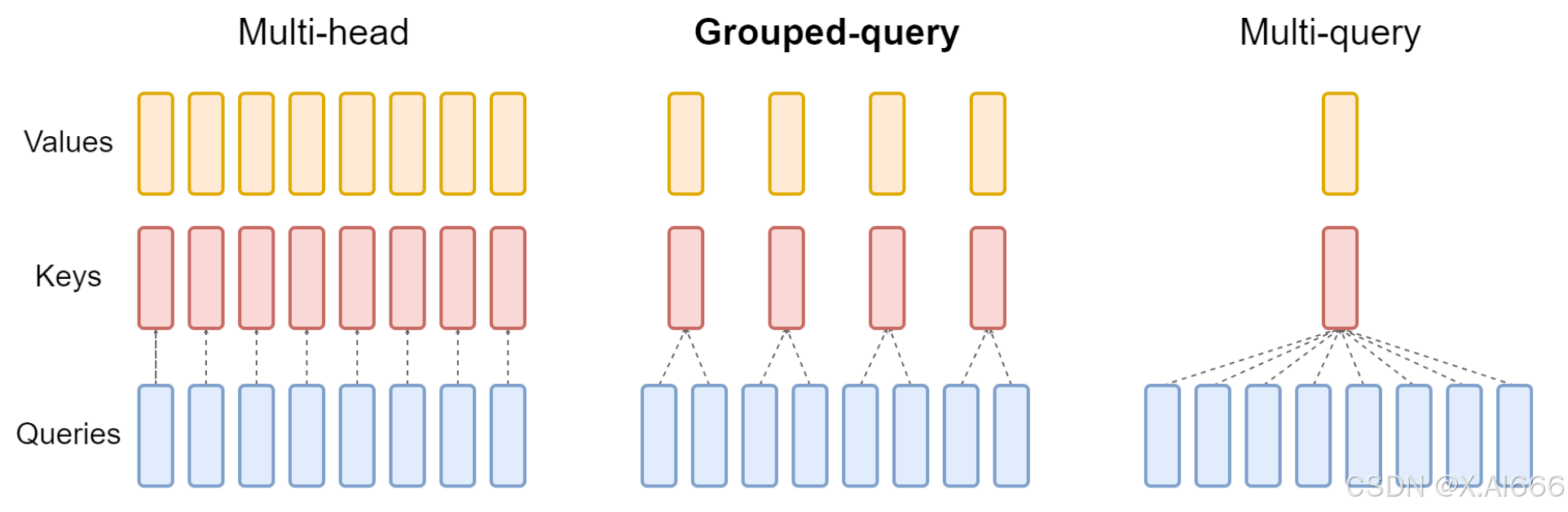
【大模型LLM面试合集】大语言模型架构_MHA_MQA_GQA
MHA_MQA_GQA 1.总结 在 MHA(Multi Head Attention) 中,每个头有自己单独的 key-value 对;标准的多头注意力机制,h个Query、Key 和 Value 矩阵。在 MQA(Multi Query Attention) 中只会有一组 k…...
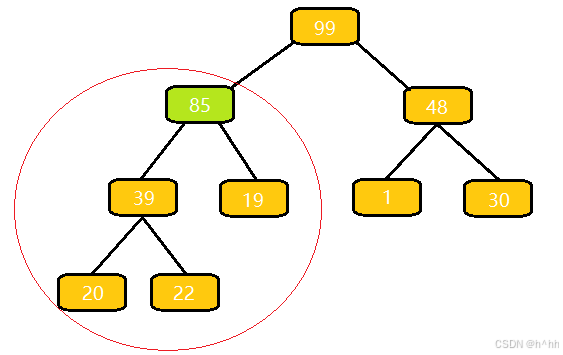
向上调整算法(详解)c++
算法流程: 与⽗结点的权值作⽐较,如果⽐它⼤,就与⽗亲交换; 交换完之后,重复 1 操作,直到⽐⽗亲⼩,或者换到根节点的位置 这里为什么插入85完后合法? 我们插入一个85,…...
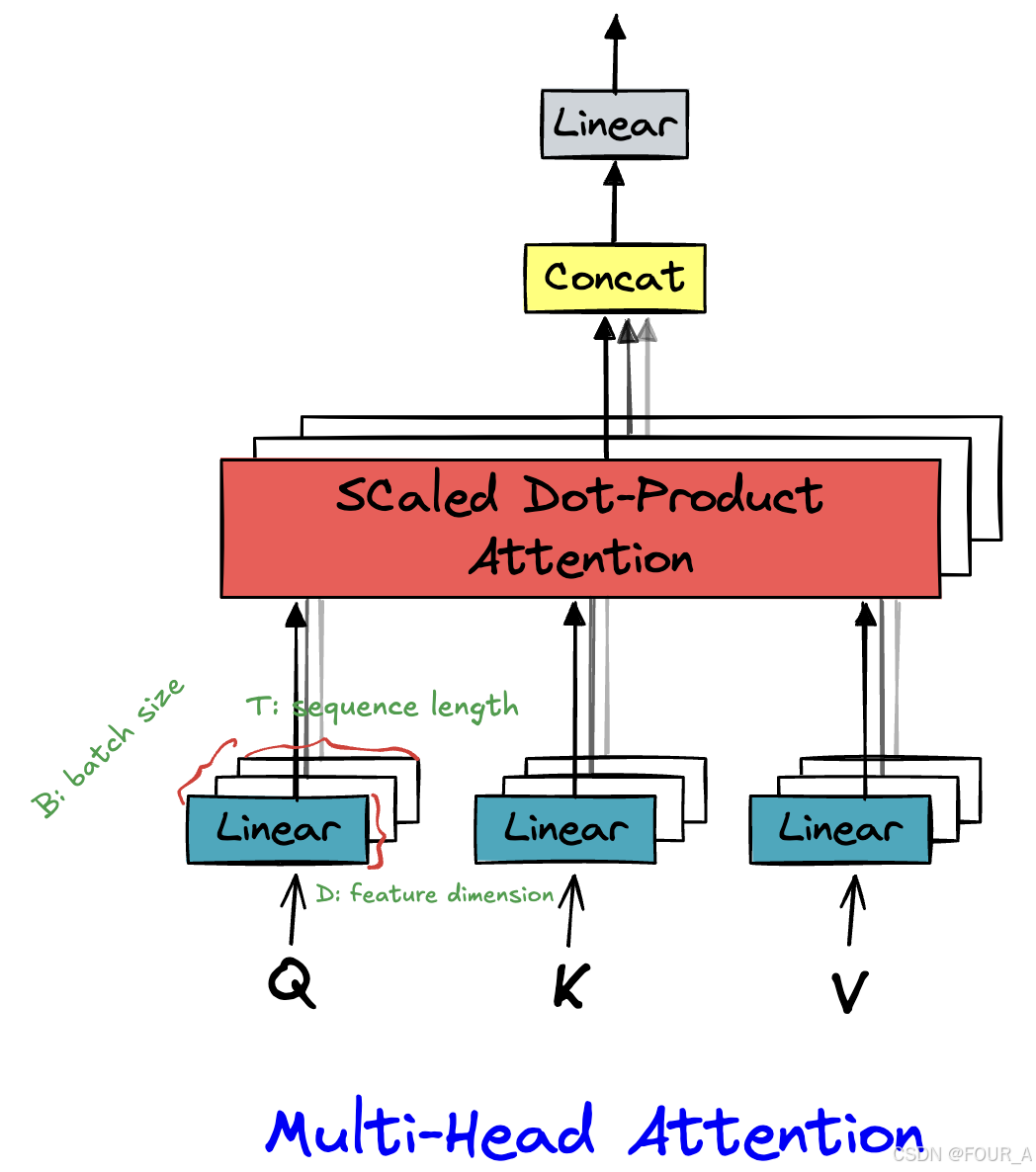
【Transformer】手撕Attention
import torch from torch import nn import torch.functional as F import mathX torch.randn(16,64,512) # B,T,Dd_model 512 # 模型的维度 n_head 8 # 注意力头的数量多头注意力机制 class multi_head_attention(nn.Module): def __init__(self, d_model, n_hea…...

844.比较含退格的字符串
目录 题目思路解法收获 题目 给定 s 和 t 两个字符串,当它们分别被输入到空白的文本编辑器后,如果两者相等,返回 true 。# 代表退格字符。 注意:如果对空文本输入退格字符,文本继续为空。 思路 如何解退格之后left…...

图书管理系统 Axios 源码__编辑图书
目录 功能概述: 代码实现(index.js): 代码解析: 图书管理系统中,删除图书功能是核心操作之一。下是基于 HTML、Bootstrap、JavaScript 和 Axios 实现的删除图书功能的详细介绍。 功能概述: …...
LabVIEW纤维集合体微电流测试仪
LabVIEW开发纤维集合体微电流测试仪。该设备精确测量纤维材料在特定电压下的电流变化,以分析纤维的结构、老化及回潮率等属性,对于纤维材料的科学研究及质量控制具有重要意义。 项目背景 在纤维材料的研究与应用中,电学性能是评估其性能…...

Commander 一款命令行自定义命令依赖
一、安装 commander 插件 npm install commander 二、基本用法 1. 创建一个简单的命令行程序 创建一个 JavaScript 文件,例如 mycli.js,并添加以下代码: // 引入 commander 模块并获取 program 对象。const { program } require("…...
)
Day24 洛谷普及2004(内涵前缀和与差分算法)
零基础洛谷刷题记录 Day01 2024.11.18 Day02 2024.11.25 Day03 2024.11.26 Day04 2024.11.28 Day05 2024.11.29 Day06 2024 12.02 Day07 2024.12.03 Day08 2024 12 05 Day09 2024.12.07 Day10 2024.12.09 Day11 2024.12.10 Day12 2024.12.12 Day13 2024.12.16 Day14 2024.12.1…...
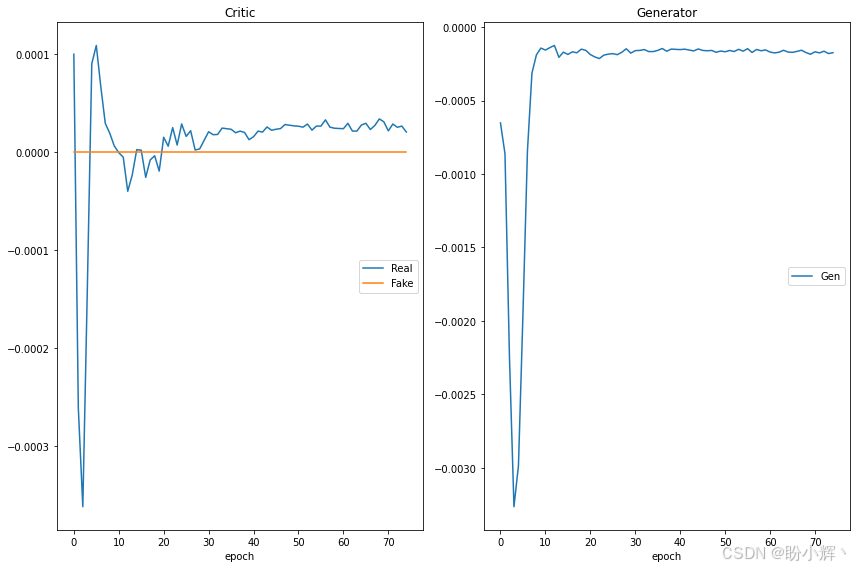
遗传算法与深度学习实战(33)——WGAN详解与实现
遗传算法与深度学习实战(33)——WGAN详解与实现 0. 前言1. 训练生成对抗网络的挑战2. GAN 优化问题2.1 梯度消失2.2 模式崩溃 2.3 无法收敛3 Wasserstein GAN3.1 Wasserstein 损失3.2 使用 Wasserstein 损失改进 DCGAN 小结系列链接 0. 前言 原始的生成…...
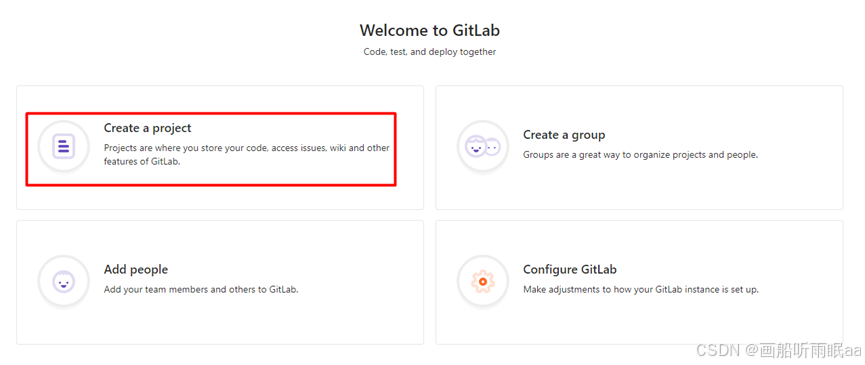
gitlab云服务器配置
目录 1、关闭防火墙 2、安装gitlab 3、修改配置 4、查看版本 GitLab终端常用命令 5、访问 1、关闭防火墙 firewall-cmd --state 检查防火墙状态 systemctl stop firewalld.service 停止防火墙 2、安装gitlab xftp中导入安装包 [rootgitlab ~]#mkdir -p /service/tool…...

SAP SD学习笔记27 - 请求计划(开票计划)之1 - 定期请求(定期开票)
上两章讲了贩卖契约(框架协议)的概要,以及贩卖契约中最为常用的 基本契约 - 数量契约和金额契约。 SAP SD学习笔记26 - 贩卖契约(框架协议)的概要,基本契约 - 数量契约_sap 框架协议-CSDN博客 SAP SD学习笔记27 - 贩卖契约(框架…...

HTML DOM 修改 HTML 内容
HTML DOM 修改 HTML 内容 引言 HTML DOM(文档对象模型)是浏览器内部用来解析和操作HTML文档的一种机制。通过DOM,我们可以轻松地修改HTML文档的结构、样式和行为。本文将详细介绍如何使用HTML DOM来修改HTML内容,包括元素的增删改查、属性修改以及事件处理等。 1. HTML …...

基于VMware的ubuntu与vscode建立ssh连接
1.首先安装openssh服务 sudo apt update sudo apt install openssh-server -y 2.启动并检查ssh服务状态 到这里可以按q退出 之后输入命令 : ip a 红色挡住的部分就是我们要的地址,这里就不展示了哈 3.配置vscode 打开vscode 搜索并安装:…...
Flutter Candies 一桶天下
| | | | | | | | 入魔的冬瓜 最近刚入桶的兄弟,有责任心的开发者,对自己的项目会不断进行优化,达到最完美的状态 自定义日历组件 主要功能 支持公历,农历,节气,传统节日,常用节假日 …...

maven如何不把依赖的jar打包到同一个jar?
spring boot项目打jar包部署: 经过以下步骤, 最终会形成maven依赖的多个jar(包括lib下添加的)、 我们编写的程序代码打成一个jar,将程序jar与 依赖jar分开,便于管理: success: 最终…...

HTML5 技术深度解读:本地存储与地理定位的最佳实践
系列文章目录 01-从零开始学 HTML:构建网页的基本框架与技巧 02-HTML常见文本标签解析:从基础到进阶的全面指南 03-HTML从入门到精通:链接与图像标签全解析 04-HTML 列表标签全解析:无序与有序列表的深度应用 05-HTML表格标签全面…...

AIGC技术中常提到的 “嵌入转换到同一个向量空间中”该如何理解
在AIGC(人工智能生成内容)技术中,“嵌入转换到同一个向量空间中”是一个核心概念,其主要目的是将不同类型的输入数据(如文本、图像、音频等)映射到一个统一的连续向量空间中,从而实现数据之间的…...

【机器学习理论】朴素贝叶斯网络
基础知识: 先验概率:对某个事件发生的概率的估计。可以是基于历史数据的估计,可以由专家知识得出等等。一般是单独事件概率。 后验概率:指某件事已经发生,计算事情发生是由某个因素引起的概率。一般是一个条件概率。 …...

XCTF-web-easyupload
试了试php,php7,pht,phtml等,都没有用 尝试.user.ini 抓包修改将.user.ini修改为jpg图片 在上传一个123.jpg 用蚁剑连接,得到flag...

将对透视变换后的图像使用Otsu进行阈值化,来分离黑色和白色像素。这句话中的Otsu是什么意思?
Otsu 是一种自动阈值化方法,用于将图像分割为前景和背景。它通过最小化图像的类内方差或等价地最大化类间方差来选择最佳阈值。这种方法特别适用于图像的二值化处理,能够自动确定一个阈值,将图像中的像素分为黑色和白色两类。 Otsu 方法的原…...

基于数字孪生的水厂可视化平台建设:架构与实践
分享大纲: 1、数字孪生水厂可视化平台建设背景 2、数字孪生水厂可视化平台建设架构 3、数字孪生水厂可视化平台建设成效 近几年,数字孪生水厂的建设开展的如火如荼。作为提升水厂管理效率、优化资源的调度手段,基于数字孪生的水厂可视化平台的…...

微信小程序云开发平台MySQL的连接方式
注:微信小程序云开发平台指的是腾讯云开发 先给结论:微信小程序云开发平台的MySQL,无法通过获取数据库连接信息的方式进行连接,连接只能通过云开发的SDK连接,具体要参考官方文档: 为什么? 因为…...

NLP学习路线图(二十三):长短期记忆网络(LSTM)
在自然语言处理(NLP)领域,我们时刻面临着处理序列数据的核心挑战。无论是理解句子的结构、分析文本的情感,还是实现语言的翻译,都需要模型能够捕捉词语之间依时序产生的复杂依赖关系。传统的神经网络结构在处理这种序列依赖时显得力不从心,而循环神经网络(RNN) 曾被视为…...

IoT/HCIP实验-3/LiteOS操作系统内核实验(任务、内存、信号量、CMSIS..)
文章目录 概述HelloWorld 工程C/C配置编译器主配置Makefile脚本烧录器主配置运行结果程序调用栈 任务管理实验实验结果osal 系统适配层osal_task_create 其他实验实验源码内存管理实验互斥锁实验信号量实验 CMISIS接口实验还是得JlINKCMSIS 简介LiteOS->CMSIS任务间消息交互…...

Ubuntu Cursor升级成v1.0
0. 当前版本低 使用当前 Cursor v0.50时 GitHub Copilot Chat 打不开,快捷键也不好用,当看到 Cursor 升级后,还是蛮高兴的 1. 下载 Cursor 下载地址:https://www.cursor.com/cn/downloads 点击下载 Linux (x64) ,…...

elementUI点击浏览table所选行数据查看文档
项目场景: table按照要求特定的数据变成按钮可以点击 解决方案: <el-table-columnprop"mlname"label"名称"align"center"width"180"><template slot-scope"scope"><el-buttonv-if&qu…...

Vue 模板语句的数据来源
🧩 Vue 模板语句的数据来源:全方位解析 Vue 模板(<template> 部分)中的表达式、指令绑定(如 v-bind, v-on)和插值({{ }})都在一个特定的作用域内求值。这个作用域由当前 组件…...

Unity中的transform.up
2025年6月8日,周日下午 在Unity中,transform.up是Transform组件的一个属性,表示游戏对象在世界空间中的“上”方向(Y轴正方向),且会随对象旋转动态变化。以下是关键点解析: 基本定义 transfor…...
