【机器学习理论】朴素贝叶斯网络
基础知识:
先验概率:对某个事件发生的概率的估计。可以是基于历史数据的估计,可以由专家知识得出等等。一般是单独事件概率。
后验概率:指某件事已经发生,计算事情发生是由某个因素引起的概率。一般是一个条件概率。
条件概率:条件事件发生后,另一个事件发生的概率。一般的形式为 P ( B ∣ A ) P(B|A) P(B∣A),表示 A A A发生的条件下 B B B发生的概率。
P ( B ∣ A ) = P ( A B ) P ( A ) P(B|A) = \frac {P(AB)}{P(A)} P(B∣A)=P(A)P(AB)
贝叶斯公式基于先验概率,计算后验概率的方法;公式为:
P ( A ∣ B ) = P ( B ∣ A ) ⋅ P ( A ) P ( B ) P(A|B) = \frac {P(B|A) \cdot P(A)}{P(B)} P(A∣B)=P(B)P(B∣A)⋅P(A)
- P ( A ∣ B ) P(A∣B) P(A∣B): 在事件 B B B 发生的条件下,事件 A A A 发生的概率(后验概率)。
- P ( B ∣ A ) P(B | A) P(B∣A):在事件 A A A 发生的条件下,事件 B B B 的发生概率(似然概率)。
- P ( A ) P(A) P(A):事件 A A A 发生的先验概率(先验知识)。
- P ( B ) P(B) P(B):事件 B B B 发生的总概率。
贝叶斯公式可以从条件概率和全概率公式推导得出:
- 条件概率定义:
P ( A ∣ B ) = P ( A ∩ B ) P ( B ) , P ( B ∣ A ) = P ( A ∩ B ) P ( A ) P(A | B) = \frac {P(A \cap B)}{P(B)}, P(B|A) = \frac {P(A \cap B)}{P(A)} P(A∣B)=P(B)P(A∩B),P(B∣A)=P(A)P(A∩B) - 公式联立:
P ( A ∩ B ) = P ( B ∣ A ) ⋅ P ( A ) = P ( A ∣ B ) ⋅ P ( B ) P(A \cap B) = P(B|A) \cdot P(A) = P(A | B) \cdot P(B) P(A∩B)=P(B∣A)⋅P(A)=P(A∣B)⋅P(B) - 整理得到贝叶斯公式:
P ( A ∣ B ) = P ( B ∣ A ) P ( A ) P ( B ) P(A | B) = \frac {P(B | A) P(A)}{P(B)} P(A∣B)=P(B)P(B∣A)P(A)
- 贝叶斯公式:将先验概率 P ( A ) P(A) P(A)、似然概率 P ( B ∣ A ) P(B∣A) P(B∣A) 和证据 P ( B ) P(B) P(B) 结合,计算后验概率 P ( A ∣ B ) P(A∣B) P(A∣B)。
朴素贝叶斯做出了一个假设”属性条件独立假设“:对所有已知标签的样本,假设每个属性独立地对标签结果产生影响。(这是一个很强的条件)
假设样本为: x = { a 1 , a 2 , . . . , a d } x=\{a_{1}, a_{2}, ..., a_{d} \} x={a1,a2,...,ad},label为 Y = { c 1 , c 2 , c 3 , . . . , c n } Y = \{c_{1}, c_{2}, c_{3}, ...,c_{n} \} Y={c1,c2,c3,...,cn};则计算这样一个样本 x x x 的所属类别的公式为:
P ( c k ∣ x ) = max { P ( c 1 ∣ x ) , P ( c 2 ∣ x ) , P ( c 3 ∣ x ) , . . . , P ( c n ∣ x ) } P(c_{k} | x) = \max \{ P(c_{1} |x), P(c_{2} | x), P(c_{3} | x), ..., P(c_{n} |x)\} P(ck∣x)=max{P(c1∣x),P(c2∣x),P(c3∣x),...,P(cn∣x)}
基于条件独立假设;可以得到
P ( c ∣ x ) = P ( c ) P ( x ∣ c ) P ( x ) = P ( c ) P ( x ) ∏ i = 1 d P ( x i ∣ c ) P(c|x) = \frac {P(c)P(x|c)}{P(x)} = \frac {P(c)}{P(x)} \prod_{i=1}^{d} P(x_{i}|c) P(c∣x)=P(x)P(c)P(x∣c)=P(x)P(c)i=1∏dP(xi∣c)
其中 d d d为属性数目, x i x_{i} xi为 x x x 在第 i i i 个属性上的取值。
我们重写上述公式:
h n b ( x ) = max { P ( c 1 ∣ x ) , P ( c 2 ∣ x ) , P ( c 3 ∣ x ) , . . . , P ( c n ∣ x ) } = arg max c ∈ Y P ( c ) P ( x ) ∏ i = 1 d P ( x i ∣ C ) = arg max c ∈ Y P ( c ) ∏ i = 1 d P ( x i ∣ C ) \begin{align} h_{nb}(x) &= \max \{ P(c_{1} |x), P(c_{2} | x), P(c_{3} | x), ..., P(c_{n} |x)\} \\ &= \arg \max_{c \in Y} \frac {P(c)}{P(x)} \prod_{i=1}^{d}P(x_{i} | C) \\ &= \arg \max_{c \in Y} P(c) \prod_{i=1}^{d}P(x_{i} | C) \end{align} hnb(x)=max{P(c1∣x),P(c2∣x),P(c3∣x),...,P(cn∣x)}=argc∈YmaxP(x)P(c)i=1∏dP(xi∣C)=argc∈YmaxP(c)i=1∏dP(xi∣C) 令 D c D_{c} Dc 表示训练集 D D D 中第 c c c 类样本组成的集合,若有充足的独立同分布样本,则可以容易地估计出类别的先验概率:
P ( c ) = ∣ D c ∣ ∣ D ∣ P(c) = \frac {|D_{c}|}{|D|} P(c)=∣D∣∣Dc∣
对于离散属性而言,令 D c , x i D_{c, x_{i}} Dc,xi 表示 D c D_{c} Dc 中第 i i i 个属性上取值为 x i x_{i} xi 的样本组成的集合,则条件概率 P ( x i ∣ c ) P(x_{i} |c) P(xi∣c) 可估计为:
P x i ∣ c = ∣ D c , x i ∣ ∣ D c ∣ P{x_{i} | c} = \frac {|D_{c, x_{i}}|}{|D_{c}|} Pxi∣c=∣Dc∣∣Dc,xi∣
对于连续属性可考虑概率密度函数,假定 p ( x i ∣ c ) ∼ N ( μ c , i , σ c , i 2 ) p(x_{i}|c) \sim \mathcal{N}(\mu _{c, i}, \sigma _{c,i}^{2}) p(xi∣c)∼N(μc,i,σc,i2)d,其中 μ c , i \mu_{c, i} μc,i和 σ c , i 2 \sigma_{c, i}^{2} σc,i2分别是第 c c c 类样本在第 i i i 个属性上取值的均值和方差,则有:
p ( x i ∣ c ) = 1 2 π σ c , i exp ( − ( x i − μ c , i ) 2 2 σ c , i 2 ) p(x_{i} | c) = \frac {1}{\sqrt{2 \pi} \sigma_{c, i}} \exp (- \frac {(x_{i}-\mu_{c, i})^2}{2 \sigma_{c, i}^{2}}) p(xi∣c)=2πσc,i1exp(−2σc,i2(xi−μc,i)2)
相关文章:

【机器学习理论】朴素贝叶斯网络
基础知识: 先验概率:对某个事件发生的概率的估计。可以是基于历史数据的估计,可以由专家知识得出等等。一般是单独事件概率。 后验概率:指某件事已经发生,计算事情发生是由某个因素引起的概率。一般是一个条件概率。 …...
)
Docker 部署 GLPI(IT 资产管理软件系统)
GLPI 简介 GLPI open source tool to manage Helpdesk and IT assets GLPI stands for Gestionnaire Libre de Parc Informatique(法语 资讯设备自由软件 的缩写) is a Free Asset and IT Management Software package, that provides ITIL Service De…...

【Vaadin flow 实战】第5讲-使用常用UI组件绘制页面元素
vaadin flow官方提供的UI组件文档地址是 https://vaadin.com/docs/latest/components这里,我简单实战了官方提供的一些免费的UI组件,使用案例如下: Accordion 手风琴 Accordion 手风琴效果组件 Accordion 手风琴-测试案例代码 Slf4j PageT…...

强化学习 DAY1:什么是 RL、马尔科夫决策、贝尔曼方程
第一部分 RL基础:什么是RL与MRP、MDP 1.1 入门强化学习所需掌握的基本概念 1.1.1 什么是强化学习:依据策略执行动作-感知状态-得到奖励 强化学习里面的概念、公式,相比ML/DL特别多,初学者刚学RL时,很容易被接连不断…...
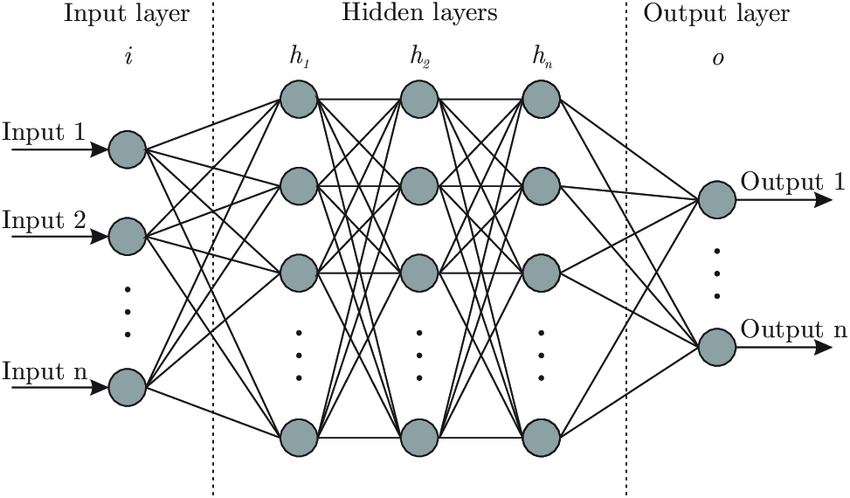
理解神经网络:Brain.js 背后的核心思想
温馨提示 这篇文章篇幅较长,主要是为后续内容做铺垫和说明。如果你觉得文字太多,可以: 先收藏,等后面文章遇到不懂的地方再回来查阅。直接跳读,重点关注加粗或高亮的部分。放心,这种“文字轰炸”不会常有的,哈哈~ 感谢你的耐心阅读!😊 欢迎来到 brain.js 的学习之旅!…...

【Docker】dockerfile识别当前构建的镜像平台
在编写dockerfile的时候,可能会遇到需要针对不同平台进行不同操作的时候,这需要我们对dockerfile进行针对性修改。 比如opencv的依赖项libjasper-dev在ubuntu18.04上就需要根据不同的平台做不同的处理,关于这个库的安装在另外一篇博客里面有…...
【VM】VirtualBox安装CentOS8虚拟机
阅读本文前,请先根据 VirtualBox软件安装教程 安装VirtualBox虚拟机软件。 1. 下载centos8系统iso镜像 可以去两个地方下载,推荐跟随本文的操作用阿里云的镜像 centos官网:https://www.centos.org/download/阿里云镜像:http://…...
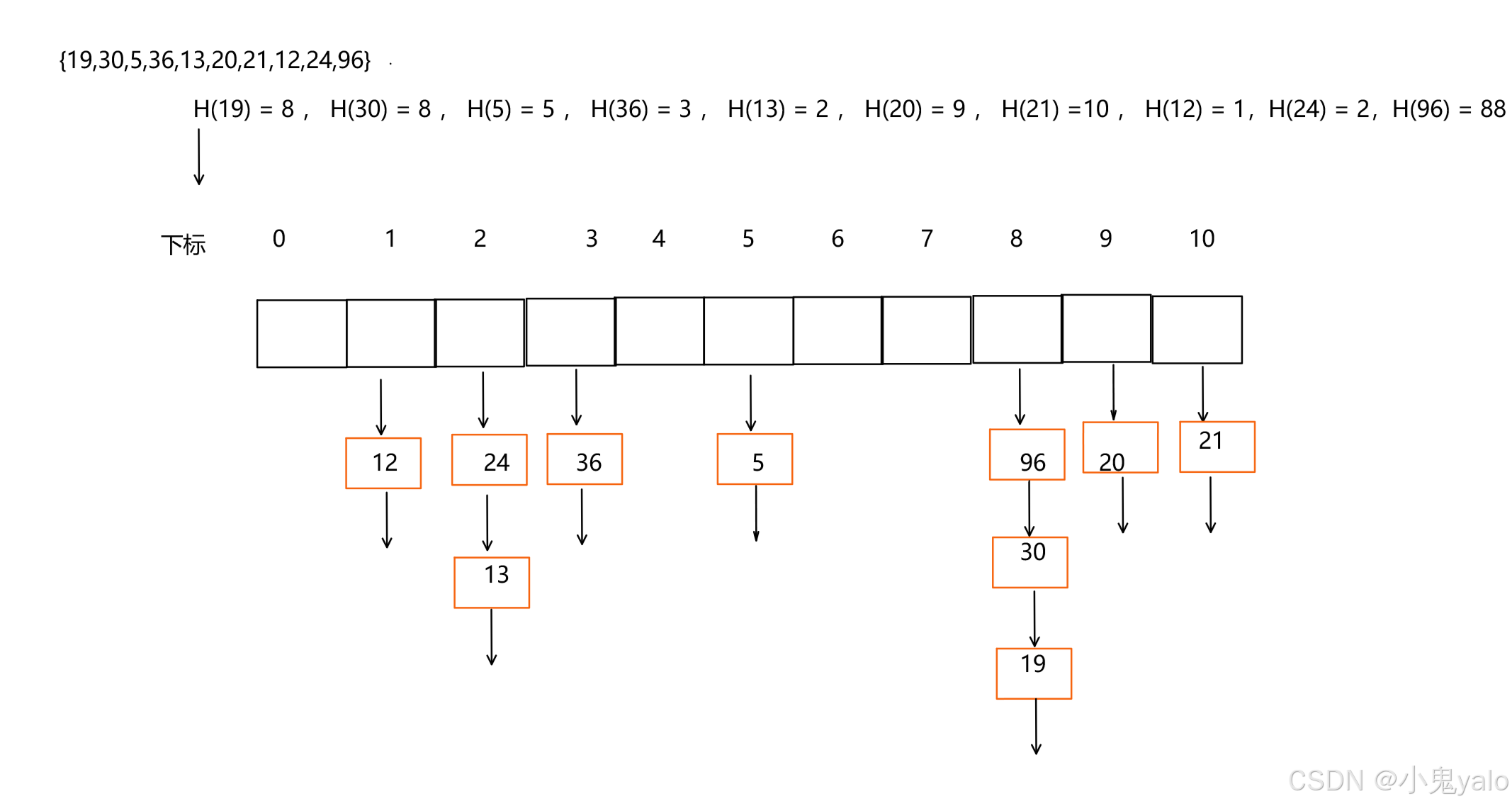
【C++篇】哈希表
目录 一,哈希概念 1.1,直接定址法 1.2,哈希冲突 1.3,负载因子 二,哈希函数 2.1,除法散列法 /除留余数法 2.2,乘法散列法 2.3,全域散列法 三,处理哈希冲突 3.1&…...

Java篇之继承
目录 一. 继承 1. 为什么需要继承 2. 继承的概念 3. 继承的语法 4. 访问父类成员 4.1 子类中访问父类的成员变量 4.2 子类中访问父类的成员方法 5. super关键字 6. super和this关键字 7. 子类构造方法 8. 代码块的执行顺序 9. protected访问修饰限定符 10. 继承方式…...

边缘检测算法(candy)
人工智能例子汇总:AI常见的算法和例子-CSDN博客 Canny 边缘检测的步骤 1. 灰度转换 如果输入的是彩色图像,则需要先转换为 灰度图像,因为边缘检测通常在单通道图像上进行。 2. 高斯滤波(Gaussian Blur) 由于边缘…...

设计模式Python版 组合模式
文章目录 前言一、组合模式二、组合模式实现方式三、组合模式示例四、组合模式在Django中的应用 前言 GOF设计模式分三大类: 创建型模式:关注对象的创建过程,包括单例模式、简单工厂模式、工厂方法模式、抽象工厂模式、原型模式和建造者模式…...
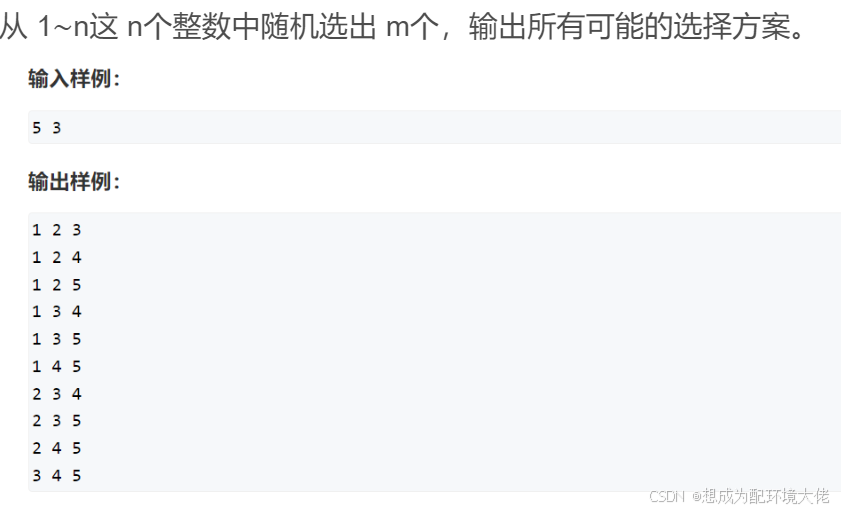
dfs枚举问题
碎碎念:要开始刷算法题备战蓝桥杯了,一切的开头一定是dfs 定义 枚举问题就是咱数学上学到的,从n个数里面选m个数,有三种题型(来自Acwing) 从 1∼n 这 n个整数中随机选取任意多个,输出所有可能的选择方案。 把 1∼n这…...
【开源免费】基于SpringBoot+Vue.JS社区智慧养老监护管理平台(JAVA毕业设计)
本文项目编号 T 163 ,文末自助获取源码 \color{red}{T163,文末自助获取源码} T163,文末自助获取源码 目录 一、系统介绍二、数据库设计三、配套教程3.1 启动教程3.2 讲解视频3.3 二次开发教程 四、功能截图五、文案资料5.1 选题背景5.2 国内…...
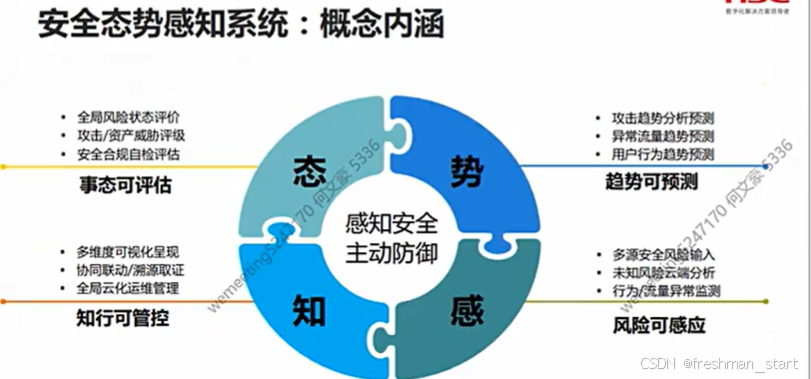
安全防护前置
就业概述 网络安全工程师/安全运维工程师/安全工程师 安全架构师/安全专员/研究院(数学要好) 厂商工程师(售前/售后) 系统集成工程师(所有计算机知识都要会一点) 学习目标 前言 网络安全事件 蠕虫病毒--&…...
高性能消息队列Disruptor
定义一个事件模型 之后创建一个java类来使用这个数据模型。 /* <h1>事件模型工程类,用于生产事件消息</h1> */ no usages public class EventMessageFactory implements EventFactory<EventMessage> { Overridepublic EventMessage newInstance(…...

kamailio中的sctp模块
以下是关于 Kamailio 配置中 enable_sctpno 的详细解释: 1. 参数作用 enable_sctp: 该参数用于控制 Kamailio 是否启用 SCTP(Stream Control Transmission Protocol) 协议支持。 设置为 yes:启用 SCTP,并加…...
)
前端学习-事件解绑,mouseover和mouseenter的区别(二十九)
目录 前言 解绑事件 语法 鼠标经过事件的区别 鼠标经过事件 示例代码 两种注册事件的区别 总结 前言 人道洛阳花似锦,偏我来时不逢春 解绑事件 on事件方式,直接使用null覆盖就可以实现事件的解绑 语法 btn.onclick function(){alert(点击了…...

独立游戏RPG回顾:高成本
刚看了某纪录片, 内容是rpg项目的回顾。也是这个以钱为核心话题的系列的最后一集。 对这期特别有代入感,因为主角是曾经的同事,曾经在某天晚上听过其项目组的争论。 对其这些年的起伏特别的能体会。 主角是制作人,在访谈中透露这…...

10.4 LangChain核心架构揭秘:模块化设计如何重塑大模型应用开发?
LangChain核心架构揭秘:模块化设计如何重塑大模型应用开发? 关键词: LangChain模块化设计、大模型开发框架、LangChain核心概念、AI应用开发、LLM工程化 一、LangChain的模块化设计哲学:从“手工作坊”到“工业化生产” 传统开发痛点: 代码重复:每个项目从零开始编写胶…...
【学习笔记】深度学习网络-正则化方法
作者选择了由 Ian Goodfellow、Yoshua Bengio 和 Aaron Courville 三位大佬撰写的《Deep Learning》(人工智能领域的经典教程,深度学习领域研究生必读教材),开始深度学习领域学习,深入全面的理解深度学习的理论知识。 在之前的文章中介绍了深度学习中用…...
)
云计算——弹性云计算器(ECS)
弹性云服务器:ECS 概述 云计算重构了ICT系统,云计算平台厂商推出使得厂家能够主要关注应用管理而非平台管理的云平台,包含如下主要概念。 ECS(Elastic Cloud Server):即弹性云服务器,是云计算…...

解决Ubuntu22.04 VMware失败的问题 ubuntu入门之二十八
现象1 打开VMware失败 Ubuntu升级之后打开VMware上报需要安装vmmon和vmnet,点击确认后如下提示 最终上报fail 解决方法 内核升级导致,需要在新内核下重新下载编译安装 查看版本 $ vmware -v VMware Workstation 17.5.1 build-23298084$ lsb_release…...

《用户共鸣指数(E)驱动品牌大模型种草:如何抢占大模型搜索结果情感高地》
在注意力分散、内容高度同质化的时代,情感连接已成为品牌破圈的关键通道。我们在服务大量品牌客户的过程中发现,消费者对内容的“有感”程度,正日益成为影响品牌传播效率与转化率的核心变量。在生成式AI驱动的内容生成与推荐环境中࿰…...

五年级数学知识边界总结思考-下册
目录 一、背景二、过程1.观察物体小学五年级下册“观察物体”知识点详解:由来、作用与意义**一、知识点核心内容****二、知识点的由来:从生活实践到数学抽象****三、知识的作用:解决实际问题的工具****四、学习的意义:培养核心素养…...
)
postgresql|数据库|只读用户的创建和删除(备忘)
CREATE USER read_only WITH PASSWORD 密码 -- 连接到xxx数据库 \c xxx -- 授予对xxx数据库的只读权限 GRANT CONNECT ON DATABASE xxx TO read_only; GRANT USAGE ON SCHEMA public TO read_only; GRANT SELECT ON ALL TABLES IN SCHEMA public TO read_only; GRANT EXECUTE O…...

oracle与MySQL数据库之间数据同步的技术要点
Oracle与MySQL数据库之间的数据同步是一个涉及多个技术要点的复杂任务。由于Oracle和MySQL的架构差异,它们的数据同步要求既要保持数据的准确性和一致性,又要处理好性能问题。以下是一些主要的技术要点: 数据结构差异 数据类型差异ÿ…...

ServerTrust 并非唯一
NSURLAuthenticationMethodServerTrust 只是 authenticationMethod 的冰山一角 要理解 NSURLAuthenticationMethodServerTrust, 首先要明白它只是 authenticationMethod 的选项之一, 并非唯一 1 先厘清概念 点说明authenticationMethodURLAuthenticationChallenge.protectionS…...

Python 包管理器 uv 介绍
Python 包管理器 uv 全面介绍 uv 是由 Astral(热门工具 Ruff 的开发者)推出的下一代高性能 Python 包管理器和构建工具,用 Rust 编写。它旨在解决传统工具(如 pip、virtualenv、pip-tools)的性能瓶颈,同时…...

push [特殊字符] present
push 🆚 present 前言present和dismiss特点代码演示 push和pop特点代码演示 前言 在 iOS 开发中,push 和 present 是两种不同的视图控制器切换方式,它们有着显著的区别。 present和dismiss 特点 在当前控制器上方新建视图层级需要手动调用…...

android13 app的触摸问题定位分析流程
一、知识点 一般来说,触摸问题都是app层面出问题,我们可以在ViewRootImpl.java添加log的方式定位;如果是touchableRegion的计算问题,就会相对比较麻烦了,需要通过adb shell dumpsys input > input.log指令,且通过打印堆栈的方式,逐步定位问题,并找到修改方案。 问题…...
