Day24 洛谷普及2004(内涵前缀和与差分算法)
零基础洛谷刷题记录
Day01 2024.11.18
Day02 2024.11.25
Day03 2024.11.26
Day04 2024.11.28
Day05 2024.11.29
Day06 2024 12.02
Day07 2024.12.03
Day08 2024 12 05
Day09 2024.12.07
Day10 2024.12.09
Day11 2024.12.10
Day12 2024.12.12
Day13 2024.12.16
Day14 2024.12.17
Day15 2024.12.18
Day16 2024.12.19
Day17 2024.12.21
Day18 2024.12.23
Day19 2024.12.24
Day20 2024.12.25
Day21 2024.12.26
Day22 2025.01.19
Day23 2025.01.21
Day24 2025.02.01
文章目录
- 零基础洛谷刷题记录
- 2004:题目描述
- 2004:AC代码
- 2004:学习成果
- 算法:一维前缀和
- 算法:一维差分
- 算法:二维前缀和
- 算法:二维差分
- 2004:代码优化
领地选择
2004:题目描述
作为在虚拟世界里统帅千军万马的领袖,小 Z 认为天时、地利、人和三者是缺一不可的,所以,谨慎地选择首都的位置对于小 Z 来说是非常重要的。
首都被认为是一个占地 C×C 的正方形。小 Z 希望你寻找到一个合适的位置,使得首都所占领的位置的土地价值和最高。
2004:AC代码
#define _CRT_SECURE_NO_WARNINGS 1
#include<stdio.h>
#include<string.h>
#include<math.h>int main()
{static int arr[1005][1005];int ditu_kuan, ditu_chang, shoudu_bianchang;scanf("%d %d %d", &ditu_kuan, &ditu_chang, &shoudu_bianchang);for (int i = 1; i <= ditu_kuan; i++){for (int j = 1; j <= ditu_chang; j++){scanf("%d", &arr[i][j]);}}int shoudu_hang = 0, shoudu_zhong = 0;int max = 0;for (int i = 1; i <= ditu_chang - shoudu_bianchang + 1;i++){for (int j = 1; j <= ditu_kuan - shoudu_bianchang + 1;j++){int jiazhi = 0;int hang = i;while (hang <= i + shoudu_bianchang - 1){int lie = j;while (lie < j + shoudu_bianchang){jiazhi += arr[hang][lie];lie++;}hang++;}if (jiazhi > max){shoudu_hang = i;shoudu_zhong = j;max = jiazhi;}}}printf("%d %d\n", shoudu_hang, shoudu_zhong);return 0;
}
2004:学习成果
- 是一道简单的比较题,但是对时间复杂度如何优化呢
一维前缀和
算法:一维前缀和
- 对于数组arr={1,3,7,5,2},进行q次询问,例如询问【2,4】、【0,3】、【3,4】求和,会有几个数的和进行了重复的计算,时间复杂度是0(nq)
- 前缀和数组的撰写:
> 若 arr={1,3,7,5,2}
> 则 sum{1,1+3=4,7+4=11,11+5=16,16+2=18}
> 其中sum【i】=sum【0】+sum【1】+...+sum【i】=sum【i-1】+arr【i】
> 由此得到arr【i】+arr【i+1】+...+arr【j】=sum【j】-sum【i-1】
一维差分
算法:一维差分
- 对于数组arr={1,3,7,5,2},进行m次操作,给区间【i,j】中的每个元素都+value,并询问arr的更新结果,复杂度为O(mn)
- 优化思路:由于我们只关心各种操作的结果,而不关心过程(例如对a-5+3+1-2其实就是a-3)
- 引入差分数组
> 对于arr={1,3,7,5,2}
> 差分数组d={1,2,4,-2,-3}
> 观察前缀和数组sum_d={1,3,4,7,2}
> 总结:前缀和是差分的逆运算
- 差分标记
[L,R]+value = d[L]+value,d[R+1]+value//中间都+ value 所以中间差分是不变的,d[R+1]可能不存在
此时时间复杂度变为O(2m+n)
二维前缀和
算法:二维前缀和
- 对于二维矩阵arr【10】【10】,若想计算由arr【2】【2】和arr【5】【5】围成的矩阵元素的和,原始做法就是一个一个累加,时间复杂度为O(mn)
- 优化思路:利用二维前缀和将问题转化为【0,0】到【i,j】的提取算好的简单计算
- 计算公式
sum(【i】【j】到【m】【n】)=sum【m】【n】-sum【i-1】【j】-sum【i】【j-1】+sum【i-1】【j-1】//没写哪到哪,默认(0,0),注意i-1和j-1的越界情况,也可以把下标从1开始避免越界的问题
- 二维前缀和数组的构造
就是利用上面的计算公式即可得到
算法:二维差分
- 对于二维矩阵arr【10】【10】,若想计算由arr【2】【2】和arr【5】【5】围成的矩阵元素都+3,再将由arr【1】【1】和arr【3】【4】围成的矩阵元素都-6,原始做法就是一个一个加,再一个一个减,时间复杂度为O(mn)
- 优化思路:利用差分进行差分标记,将内部的加减转化为差分边界的加减
- 差分标记的影响:将d【i】【j】+1,会导致d【i】【j】的右下角矩阵元素都+1
- 差分标记的公式:
在n×n的矩阵中,将arr【i】【j】到arr【m】【l】的元素都+value,则
d【i】【j】+value
d【i】【l+1】-value
d【m+1】【j】-value
d【m+1】【l+1】+value
2004:代码优化
#define _CRT_SECURE_NO_WARNINGS 1
#include<stdio.h>
#include<string.h>
#include<math.h>int main()
{static long long int arr[1005][1005];int ditu_kuan, ditu_chang, shoudu_bianchang;scanf("%d %d %d", &ditu_kuan, &ditu_chang, &shoudu_bianchang);for (int i = 1; i <= ditu_kuan; i++){for (int j = 1; j <= ditu_chang; j++){scanf("%lld", &arr[i][j]);}}//构建二维前缀和数组static long long int sum[1005][1005] = { 0 };for (int i = 1; i <= ditu_kuan; i++){for (int j = 1; j <= ditu_chang; j++){sum[i][j] = sum[i - 1][j] + sum[i][j - 1] - sum[i - 1][j - 1] + arr[i][j];}}int shoudu_hang = 0, shoudu_zhong = 0;long long int max = 0;for (int i = shoudu_bianchang; i <= ditu_chang; i++){for (int j = shoudu_bianchang; j <= ditu_kuan; j++){if (sum[i][j] - sum[i][j - shoudu_bianchang] - sum[i - shoudu_bianchang][j] + sum[i - shoudu_bianchang][j - shoudu_bianchang] > max){shoudu_hang = i - shoudu_bianchang + 1;shoudu_zhong = j - shoudu_bianchang + 1;max = sum[i][j] - sum[i][j - shoudu_bianchang] - sum[i - shoudu_bianchang][j] + sum[i - shoudu_bianchang][j - shoudu_bianchang];}}}printf("%lld %lld\n", shoudu_hang, shoudu_zhong);return 0;
}
- 记得开long long
相关文章:
)
Day24 洛谷普及2004(内涵前缀和与差分算法)
零基础洛谷刷题记录 Day01 2024.11.18 Day02 2024.11.25 Day03 2024.11.26 Day04 2024.11.28 Day05 2024.11.29 Day06 2024 12.02 Day07 2024.12.03 Day08 2024 12 05 Day09 2024.12.07 Day10 2024.12.09 Day11 2024.12.10 Day12 2024.12.12 Day13 2024.12.16 Day14 2024.12.1…...
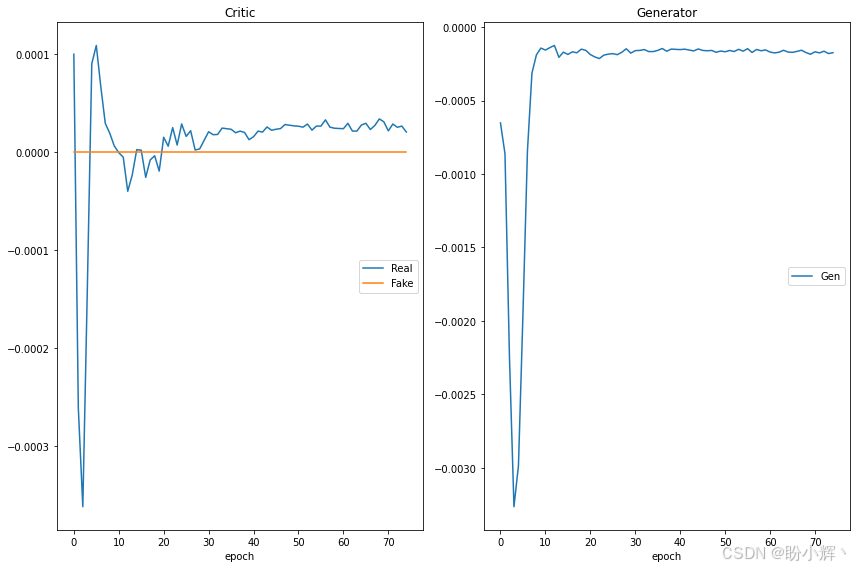
遗传算法与深度学习实战(33)——WGAN详解与实现
遗传算法与深度学习实战(33)——WGAN详解与实现 0. 前言1. 训练生成对抗网络的挑战2. GAN 优化问题2.1 梯度消失2.2 模式崩溃 2.3 无法收敛3 Wasserstein GAN3.1 Wasserstein 损失3.2 使用 Wasserstein 损失改进 DCGAN 小结系列链接 0. 前言 原始的生成…...
gitlab云服务器配置
目录 1、关闭防火墙 2、安装gitlab 3、修改配置 4、查看版本 GitLab终端常用命令 5、访问 1、关闭防火墙 firewall-cmd --state 检查防火墙状态 systemctl stop firewalld.service 停止防火墙 2、安装gitlab xftp中导入安装包 [rootgitlab ~]#mkdir -p /service/tool…...

SAP SD学习笔记27 - 请求计划(开票计划)之1 - 定期请求(定期开票)
上两章讲了贩卖契约(框架协议)的概要,以及贩卖契约中最为常用的 基本契约 - 数量契约和金额契约。 SAP SD学习笔记26 - 贩卖契约(框架协议)的概要,基本契约 - 数量契约_sap 框架协议-CSDN博客 SAP SD学习笔记27 - 贩卖契约(框架…...

HTML DOM 修改 HTML 内容
HTML DOM 修改 HTML 内容 引言 HTML DOM(文档对象模型)是浏览器内部用来解析和操作HTML文档的一种机制。通过DOM,我们可以轻松地修改HTML文档的结构、样式和行为。本文将详细介绍如何使用HTML DOM来修改HTML内容,包括元素的增删改查、属性修改以及事件处理等。 1. HTML …...

基于VMware的ubuntu与vscode建立ssh连接
1.首先安装openssh服务 sudo apt update sudo apt install openssh-server -y 2.启动并检查ssh服务状态 到这里可以按q退出 之后输入命令 : ip a 红色挡住的部分就是我们要的地址,这里就不展示了哈 3.配置vscode 打开vscode 搜索并安装:…...
Flutter Candies 一桶天下
| | | | | | | | 入魔的冬瓜 最近刚入桶的兄弟,有责任心的开发者,对自己的项目会不断进行优化,达到最完美的状态 自定义日历组件 主要功能 支持公历,农历,节气,传统节日,常用节假日 …...

maven如何不把依赖的jar打包到同一个jar?
spring boot项目打jar包部署: 经过以下步骤, 最终会形成maven依赖的多个jar(包括lib下添加的)、 我们编写的程序代码打成一个jar,将程序jar与 依赖jar分开,便于管理: success: 最终…...

HTML5 技术深度解读:本地存储与地理定位的最佳实践
系列文章目录 01-从零开始学 HTML:构建网页的基本框架与技巧 02-HTML常见文本标签解析:从基础到进阶的全面指南 03-HTML从入门到精通:链接与图像标签全解析 04-HTML 列表标签全解析:无序与有序列表的深度应用 05-HTML表格标签全面…...

AIGC技术中常提到的 “嵌入转换到同一个向量空间中”该如何理解
在AIGC(人工智能生成内容)技术中,“嵌入转换到同一个向量空间中”是一个核心概念,其主要目的是将不同类型的输入数据(如文本、图像、音频等)映射到一个统一的连续向量空间中,从而实现数据之间的…...

【机器学习理论】朴素贝叶斯网络
基础知识: 先验概率:对某个事件发生的概率的估计。可以是基于历史数据的估计,可以由专家知识得出等等。一般是单独事件概率。 后验概率:指某件事已经发生,计算事情发生是由某个因素引起的概率。一般是一个条件概率。 …...
)
Docker 部署 GLPI(IT 资产管理软件系统)
GLPI 简介 GLPI open source tool to manage Helpdesk and IT assets GLPI stands for Gestionnaire Libre de Parc Informatique(法语 资讯设备自由软件 的缩写) is a Free Asset and IT Management Software package, that provides ITIL Service De…...

【Vaadin flow 实战】第5讲-使用常用UI组件绘制页面元素
vaadin flow官方提供的UI组件文档地址是 https://vaadin.com/docs/latest/components这里,我简单实战了官方提供的一些免费的UI组件,使用案例如下: Accordion 手风琴 Accordion 手风琴效果组件 Accordion 手风琴-测试案例代码 Slf4j PageT…...

强化学习 DAY1:什么是 RL、马尔科夫决策、贝尔曼方程
第一部分 RL基础:什么是RL与MRP、MDP 1.1 入门强化学习所需掌握的基本概念 1.1.1 什么是强化学习:依据策略执行动作-感知状态-得到奖励 强化学习里面的概念、公式,相比ML/DL特别多,初学者刚学RL时,很容易被接连不断…...
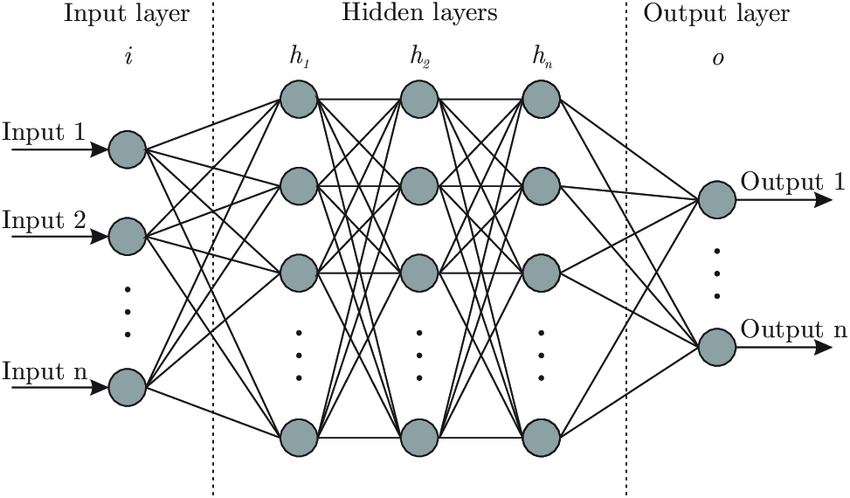
理解神经网络:Brain.js 背后的核心思想
温馨提示 这篇文章篇幅较长,主要是为后续内容做铺垫和说明。如果你觉得文字太多,可以: 先收藏,等后面文章遇到不懂的地方再回来查阅。直接跳读,重点关注加粗或高亮的部分。放心,这种“文字轰炸”不会常有的,哈哈~ 感谢你的耐心阅读!😊 欢迎来到 brain.js 的学习之旅!…...

【Docker】dockerfile识别当前构建的镜像平台
在编写dockerfile的时候,可能会遇到需要针对不同平台进行不同操作的时候,这需要我们对dockerfile进行针对性修改。 比如opencv的依赖项libjasper-dev在ubuntu18.04上就需要根据不同的平台做不同的处理,关于这个库的安装在另外一篇博客里面有…...
【VM】VirtualBox安装CentOS8虚拟机
阅读本文前,请先根据 VirtualBox软件安装教程 安装VirtualBox虚拟机软件。 1. 下载centos8系统iso镜像 可以去两个地方下载,推荐跟随本文的操作用阿里云的镜像 centos官网:https://www.centos.org/download/阿里云镜像:http://…...
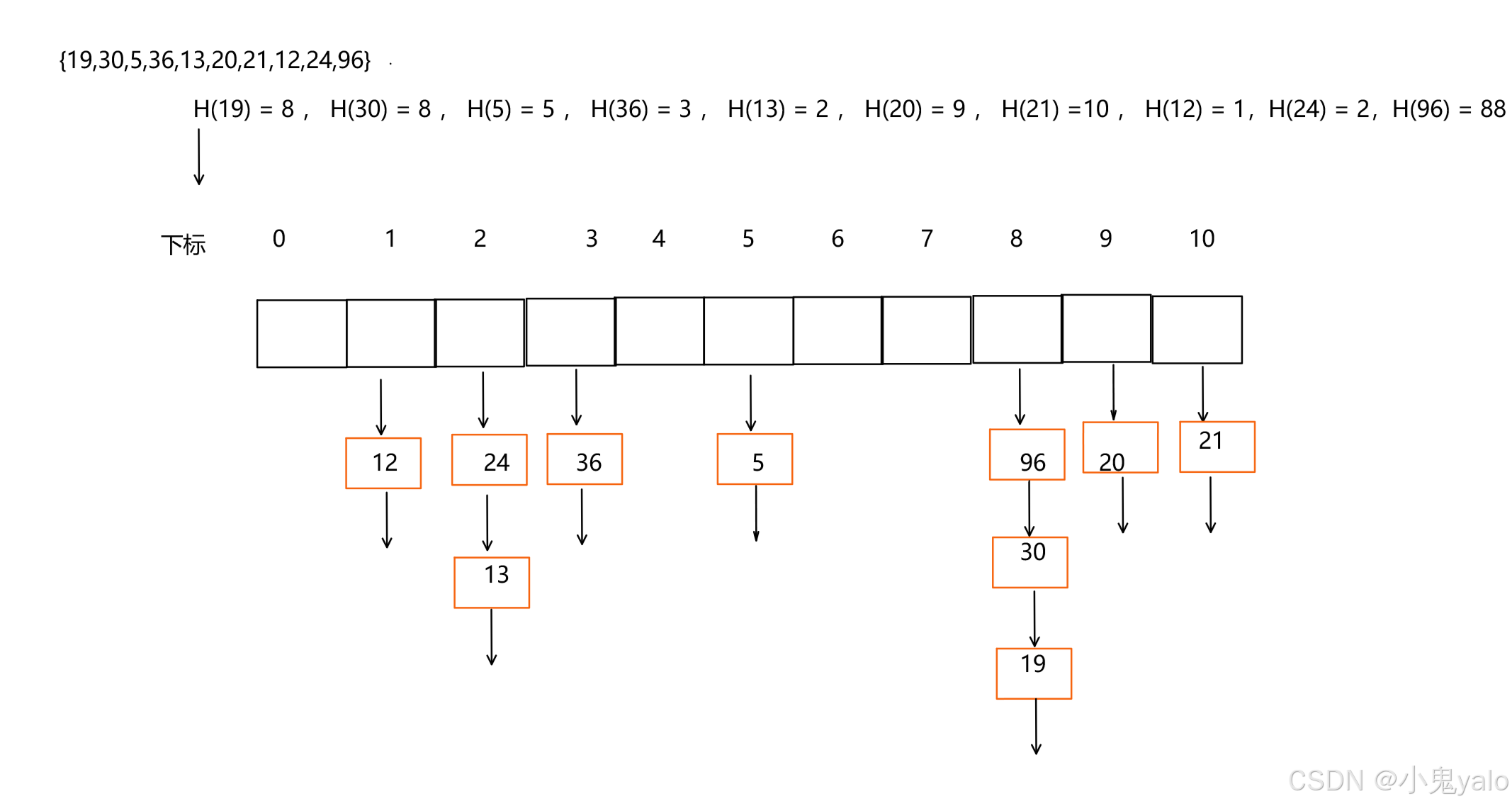
【C++篇】哈希表
目录 一,哈希概念 1.1,直接定址法 1.2,哈希冲突 1.3,负载因子 二,哈希函数 2.1,除法散列法 /除留余数法 2.2,乘法散列法 2.3,全域散列法 三,处理哈希冲突 3.1&…...

Java篇之继承
目录 一. 继承 1. 为什么需要继承 2. 继承的概念 3. 继承的语法 4. 访问父类成员 4.1 子类中访问父类的成员变量 4.2 子类中访问父类的成员方法 5. super关键字 6. super和this关键字 7. 子类构造方法 8. 代码块的执行顺序 9. protected访问修饰限定符 10. 继承方式…...

边缘检测算法(candy)
人工智能例子汇总:AI常见的算法和例子-CSDN博客 Canny 边缘检测的步骤 1. 灰度转换 如果输入的是彩色图像,则需要先转换为 灰度图像,因为边缘检测通常在单通道图像上进行。 2. 高斯滤波(Gaussian Blur) 由于边缘…...

Cursor实现用excel数据填充word模版的方法
cursor主页:https://www.cursor.com/ 任务目标:把excel格式的数据里的单元格,按照某一个固定模版填充到word中 文章目录 注意事项逐步生成程序1. 确定格式2. 调试程序 注意事项 直接给一个excel文件和最终呈现的word文件的示例,…...

k8s从入门到放弃之Ingress七层负载
k8s从入门到放弃之Ingress七层负载 在Kubernetes(简称K8s)中,Ingress是一个API对象,它允许你定义如何从集群外部访问集群内部的服务。Ingress可以提供负载均衡、SSL终结和基于名称的虚拟主机等功能。通过Ingress,你可…...

从零实现富文本编辑器#5-编辑器选区模型的状态结构表达
先前我们总结了浏览器选区模型的交互策略,并且实现了基本的选区操作,还调研了自绘选区的实现。那么相对的,我们还需要设计编辑器的选区表达,也可以称为模型选区。编辑器中应用变更时的操作范围,就是以模型选区为基准来…...
)
Java入门学习详细版(一)
大家好,Java 学习是一个系统学习的过程,核心原则就是“理论 实践 坚持”,并且需循序渐进,不可过于着急,本篇文章推出的这份详细入门学习资料将带大家从零基础开始,逐步掌握 Java 的核心概念和编程技能。 …...

JAVA后端开发——多租户
数据隔离是多租户系统中的核心概念,确保一个租户(在这个系统中可能是一个公司或一个独立的客户)的数据对其他租户是不可见的。在 RuoYi 框架(您当前项目所使用的基础框架)中,这通常是通过在数据表中增加一个…...

视频行为标注工具BehaviLabel(源码+使用介绍+Windows.Exe版本)
前言: 最近在做行为检测相关的模型,用的是时空图卷积网络(STGCN),但原有kinetic-400数据集数据质量较低,需要进行细粒度的标注,同时粗略搜了下已有开源工具基本都集中于图像分割这块,…...

PAN/FPN
import torch import torch.nn as nn import torch.nn.functional as F import mathclass LowResQueryHighResKVAttention(nn.Module):"""方案 1: 低分辨率特征 (Query) 查询高分辨率特征 (Key, Value).输出分辨率与低分辨率输入相同。"""def __…...

【堆垛策略】设计方法
堆垛策略的设计是积木堆叠系统的核心,直接影响堆叠的稳定性、效率和容错能力。以下是分层次的堆垛策略设计方法,涵盖基础规则、优化算法和容错机制: 1. 基础堆垛规则 (1) 物理稳定性优先 重心原则: 大尺寸/重量积木在下…...

如何配置一个sql server使得其它用户可以通过excel odbc获取数据
要让其他用户通过 Excel 使用 ODBC 连接到 SQL Server 获取数据,你需要完成以下配置步骤: ✅ 一、在 SQL Server 端配置(服务器设置) 1. 启用 TCP/IP 协议 打开 “SQL Server 配置管理器”。导航到:SQL Server 网络配…...

Vue3中的computer和watch
computed的写法 在页面中 <div>{{ calcNumber }}</div>script中 写法1 常用 import { computed, ref } from vue; let price ref(100);const priceAdd () > { //函数方法 price 1price.value ; }//计算属性 let calcNumber computed(() > {return ${p…...
