代码随想录算法训练营第四十二天-动态规划-股票-188.买卖股票的最佳时机IV
- 题目要求进行k次买卖
- 其实就是上一题的扩展,把2次扩展为k次
- 定义动规数组依然是二维,第一个维度表示第几天,第二个维度表示第几次买入和卖出
- 所以第二个维度的长度应该是
2k+1 - 在for循环内,要使用一个内循环来表示第几次买入或卖出,根据上一题的过程,可以发现其中的规律
class Solution {
public:int maxProfit(int k, std::vector<int>& prices) {int len = prices.size();if (len == 0) {return 0;}std::vector<std::vector<int>> dp(len, std::vector<int>(2 * k + 2, 0));for (int i = 0; i < 2 * k; i += 2) {dp[0][i + 1] = -prices[0];}for (int i = 1; i < len; ++i) {for (int j = 0; j < 2 * k; j += 2) {dp[i][j + 1] = std::max(dp[i - 1][j + 1], dp[i - 1][j] - prices[i]);dp[i][j + 2] = std::max(dp[i - 1][j + 2], dp[i - 1][j + 1] + prices[i]);}}return dp[len - 1][2 * k];}
};
- 汇总
相关文章:

代码随想录算法训练营第四十二天-动态规划-股票-188.买卖股票的最佳时机IV
题目要求进行k次买卖其实就是上一题的扩展,把2次扩展为k次定义动规数组依然是二维,第一个维度表示第几天,第二个维度表示第几次买入和卖出所以第二个维度的长度应该是2k1在for循环内,要使用一个内循环来表示第几次买入或卖出&…...
Gradle配置指南:深入解析settings.gradle.kts(Kotlin DSL版)
文章目录 Gradle配置指南:深入解析settings.gradle.kts(Kotlin DSL版)settings.gradle.kts 基础配置选项单项目配置多项目配置 高级配置选项插件管理(Plugin Management)基础配置模板案例:Android项目标准配…...
软件工程经济学-日常作业+大作业
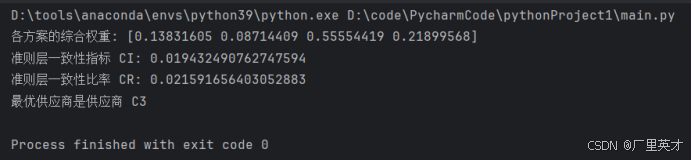
目录 一、作业1 作业内容 解答 二、作业2 作业内容 解答 三、作业3 作业内容 解答 四、大作业 作业内容 解答 1.建立层次结构模型 (1)目标层 (2)准则层 (3)方案层 2.构造判断矩阵 (1)准则层判断矩阵 (2)方案层判断矩阵 3.层次单排序及其一致性检验 代码 …...
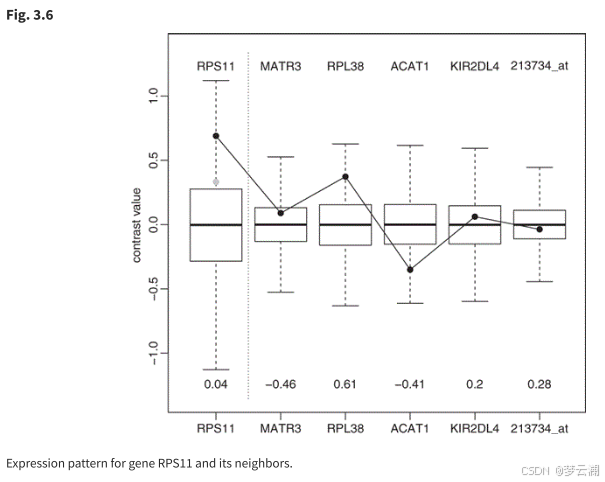
论文阅读(三):微阵列数据的图形模型和多变量分析
1.论文链接:Graphical Models and Multivariate Analysis of Microarray Data 摘要: 基因表达数据的通常分析忽略了基因表达值之间的相关性。从生物学上讲,这种假设是不合理的。本章介绍的方法允许通过稀疏高斯图形模型来描述基因之间的相关…...
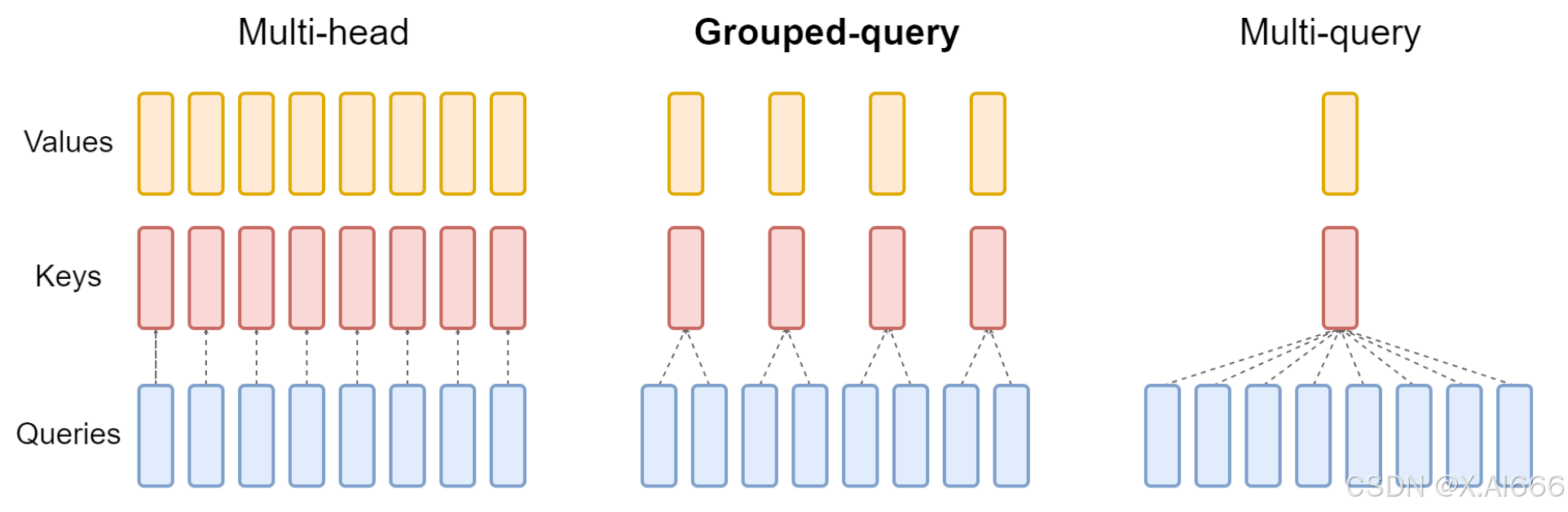
【大模型LLM面试合集】大语言模型架构_MHA_MQA_GQA
MHA_MQA_GQA 1.总结 在 MHA(Multi Head Attention) 中,每个头有自己单独的 key-value 对;标准的多头注意力机制,h个Query、Key 和 Value 矩阵。在 MQA(Multi Query Attention) 中只会有一组 k…...
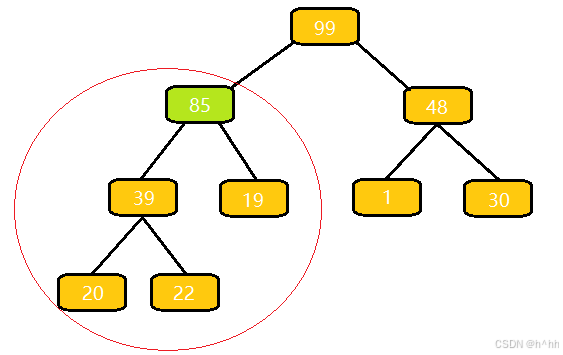
向上调整算法(详解)c++
算法流程: 与⽗结点的权值作⽐较,如果⽐它⼤,就与⽗亲交换; 交换完之后,重复 1 操作,直到⽐⽗亲⼩,或者换到根节点的位置 这里为什么插入85完后合法? 我们插入一个85,…...
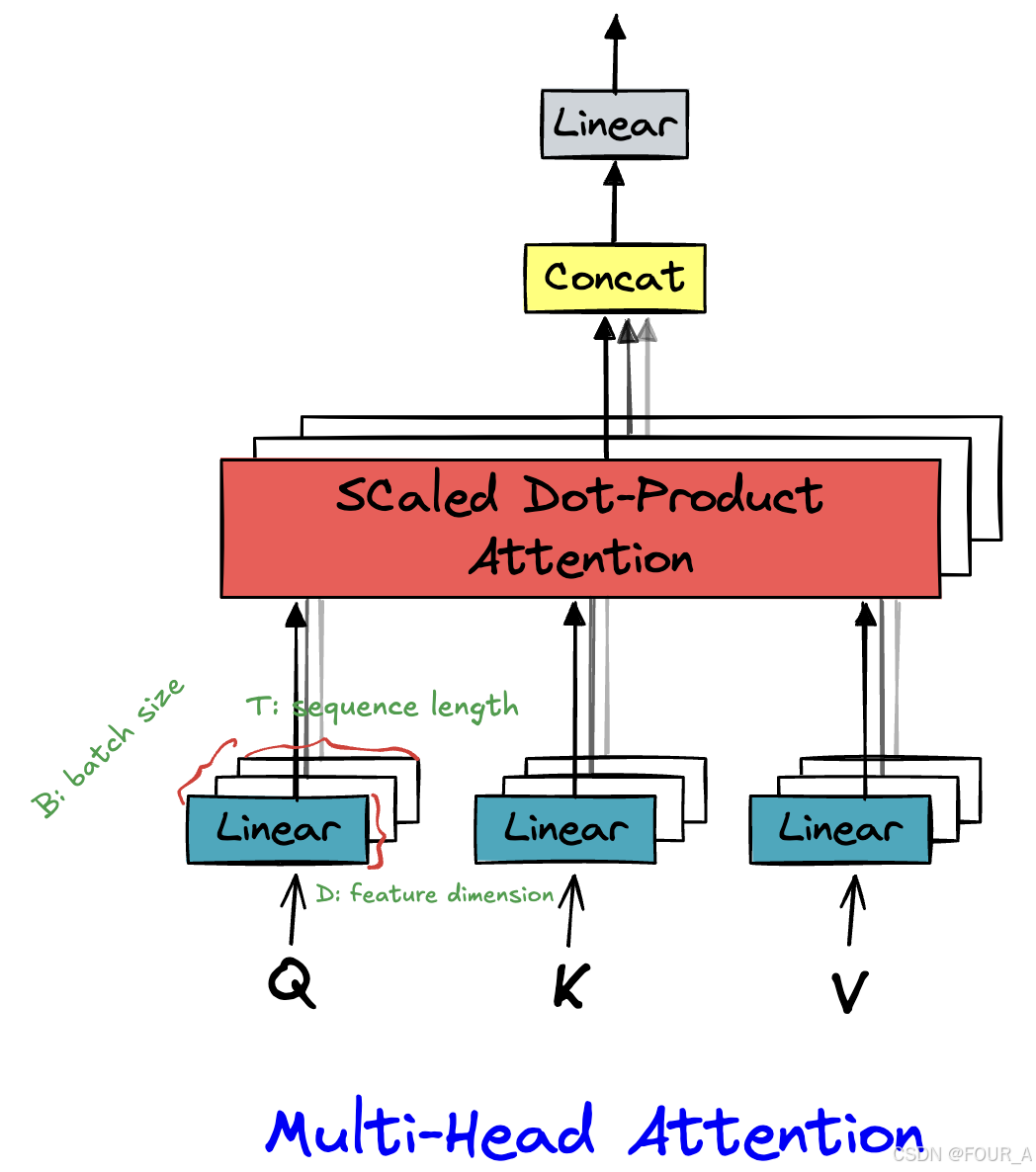
【Transformer】手撕Attention
import torch from torch import nn import torch.functional as F import mathX torch.randn(16,64,512) # B,T,Dd_model 512 # 模型的维度 n_head 8 # 注意力头的数量多头注意力机制 class multi_head_attention(nn.Module): def __init__(self, d_model, n_hea…...

844.比较含退格的字符串
目录 题目思路解法收获 题目 给定 s 和 t 两个字符串,当它们分别被输入到空白的文本编辑器后,如果两者相等,返回 true 。# 代表退格字符。 注意:如果对空文本输入退格字符,文本继续为空。 思路 如何解退格之后left…...

图书管理系统 Axios 源码__编辑图书
目录 功能概述: 代码实现(index.js): 代码解析: 图书管理系统中,删除图书功能是核心操作之一。下是基于 HTML、Bootstrap、JavaScript 和 Axios 实现的删除图书功能的详细介绍。 功能概述: …...
LabVIEW纤维集合体微电流测试仪
LabVIEW开发纤维集合体微电流测试仪。该设备精确测量纤维材料在特定电压下的电流变化,以分析纤维的结构、老化及回潮率等属性,对于纤维材料的科学研究及质量控制具有重要意义。 项目背景 在纤维材料的研究与应用中,电学性能是评估其性能…...

Commander 一款命令行自定义命令依赖
一、安装 commander 插件 npm install commander 二、基本用法 1. 创建一个简单的命令行程序 创建一个 JavaScript 文件,例如 mycli.js,并添加以下代码: // 引入 commander 模块并获取 program 对象。const { program } require("…...
)
Day24 洛谷普及2004(内涵前缀和与差分算法)
零基础洛谷刷题记录 Day01 2024.11.18 Day02 2024.11.25 Day03 2024.11.26 Day04 2024.11.28 Day05 2024.11.29 Day06 2024 12.02 Day07 2024.12.03 Day08 2024 12 05 Day09 2024.12.07 Day10 2024.12.09 Day11 2024.12.10 Day12 2024.12.12 Day13 2024.12.16 Day14 2024.12.1…...
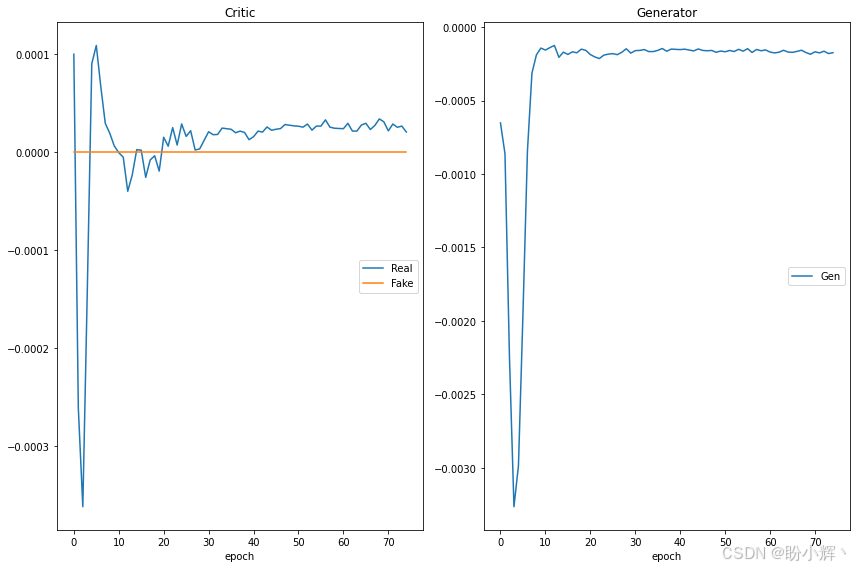
遗传算法与深度学习实战(33)——WGAN详解与实现
遗传算法与深度学习实战(33)——WGAN详解与实现 0. 前言1. 训练生成对抗网络的挑战2. GAN 优化问题2.1 梯度消失2.2 模式崩溃 2.3 无法收敛3 Wasserstein GAN3.1 Wasserstein 损失3.2 使用 Wasserstein 损失改进 DCGAN 小结系列链接 0. 前言 原始的生成…...
gitlab云服务器配置
目录 1、关闭防火墙 2、安装gitlab 3、修改配置 4、查看版本 GitLab终端常用命令 5、访问 1、关闭防火墙 firewall-cmd --state 检查防火墙状态 systemctl stop firewalld.service 停止防火墙 2、安装gitlab xftp中导入安装包 [rootgitlab ~]#mkdir -p /service/tool…...

SAP SD学习笔记27 - 请求计划(开票计划)之1 - 定期请求(定期开票)
上两章讲了贩卖契约(框架协议)的概要,以及贩卖契约中最为常用的 基本契约 - 数量契约和金额契约。 SAP SD学习笔记26 - 贩卖契约(框架协议)的概要,基本契约 - 数量契约_sap 框架协议-CSDN博客 SAP SD学习笔记27 - 贩卖契约(框架…...

HTML DOM 修改 HTML 内容
HTML DOM 修改 HTML 内容 引言 HTML DOM(文档对象模型)是浏览器内部用来解析和操作HTML文档的一种机制。通过DOM,我们可以轻松地修改HTML文档的结构、样式和行为。本文将详细介绍如何使用HTML DOM来修改HTML内容,包括元素的增删改查、属性修改以及事件处理等。 1. HTML …...

基于VMware的ubuntu与vscode建立ssh连接
1.首先安装openssh服务 sudo apt update sudo apt install openssh-server -y 2.启动并检查ssh服务状态 到这里可以按q退出 之后输入命令 : ip a 红色挡住的部分就是我们要的地址,这里就不展示了哈 3.配置vscode 打开vscode 搜索并安装:…...
Flutter Candies 一桶天下
| | | | | | | | 入魔的冬瓜 最近刚入桶的兄弟,有责任心的开发者,对自己的项目会不断进行优化,达到最完美的状态 自定义日历组件 主要功能 支持公历,农历,节气,传统节日,常用节假日 …...

maven如何不把依赖的jar打包到同一个jar?
spring boot项目打jar包部署: 经过以下步骤, 最终会形成maven依赖的多个jar(包括lib下添加的)、 我们编写的程序代码打成一个jar,将程序jar与 依赖jar分开,便于管理: success: 最终…...

HTML5 技术深度解读:本地存储与地理定位的最佳实践
系列文章目录 01-从零开始学 HTML:构建网页的基本框架与技巧 02-HTML常见文本标签解析:从基础到进阶的全面指南 03-HTML从入门到精通:链接与图像标签全解析 04-HTML 列表标签全解析:无序与有序列表的深度应用 05-HTML表格标签全面…...

[2025CVPR]DeepVideo-R1:基于难度感知回归GRPO的视频强化微调框架详解
突破视频大语言模型推理瓶颈,在多个视频基准上实现SOTA性能 一、核心问题与创新亮点 1.1 GRPO在视频任务中的两大挑战 安全措施依赖问题 GRPO使用min和clip函数限制策略更新幅度,导致: 梯度抑制:当新旧策略差异过大时梯度消失收敛困难:策略无法充分优化# 传统GRPO的梯…...

idea大量爆红问题解决
问题描述 在学习和工作中,idea是程序员不可缺少的一个工具,但是突然在有些时候就会出现大量爆红的问题,发现无法跳转,无论是关机重启或者是替换root都无法解决 就是如上所展示的问题,但是程序依然可以启动。 问题解决…...

Zustand 状态管理库:极简而强大的解决方案
Zustand 是一个轻量级、快速和可扩展的状态管理库,特别适合 React 应用。它以简洁的 API 和高效的性能解决了 Redux 等状态管理方案中的繁琐问题。 核心优势对比 基本使用指南 1. 创建 Store // store.js import create from zustandconst useStore create((set)…...

STM32标准库-DMA直接存储器存取
文章目录 一、DMA1.1简介1.2存储器映像1.3DMA框图1.4DMA基本结构1.5DMA请求1.6数据宽度与对齐1.7数据转运DMA1.8ADC扫描模式DMA 二、数据转运DMA2.1接线图2.2代码2.3相关API 一、DMA 1.1简介 DMA(Direct Memory Access)直接存储器存取 DMA可以提供外设…...

【从零学习JVM|第三篇】类的生命周期(高频面试题)
前言: 在Java编程中,类的生命周期是指类从被加载到内存中开始,到被卸载出内存为止的整个过程。了解类的生命周期对于理解Java程序的运行机制以及性能优化非常重要。本文会深入探寻类的生命周期,让读者对此有深刻印象。 目录 …...

MySQL 部分重点知识篇
一、数据库对象 1. 主键 定义 :主键是用于唯一标识表中每一行记录的字段或字段组合。它具有唯一性和非空性特点。 作用 :确保数据的完整性,便于数据的查询和管理。 示例 :在学生信息表中,学号可以作为主键ÿ…...
)
uniapp 集成腾讯云 IM 富媒体消息(地理位置/文件)
UniApp 集成腾讯云 IM 富媒体消息全攻略(地理位置/文件) 一、功能实现原理 腾讯云 IM 通过 消息扩展机制 支持富媒体类型,核心实现方式: 标准消息类型:直接使用 SDK 内置类型(文件、图片等)自…...

【Veristand】Veristand环境安装教程-Linux RT / Windows
首先声明,此教程是针对Simulink编译模型并导入Veristand中编写的,同时需要注意的是老用户编译可能用的是Veristand Model Framework,那个是历史版本,且NI不会再维护,新版本编译支持为VeriStand Model Generation Suppo…...

Cursor AI 账号纯净度维护与高效注册指南
Cursor AI 账号纯净度维护与高效注册指南:解决限制问题的实战方案 风车无限免费邮箱系统网页端使用说明|快速获取邮箱|cursor|windsurf|augment 问题背景 在成功解决 Cursor 环境配置问题后,许多开发者仍面临账号纯净度不足导致的限制问题。无论使用 16…...

在ubuntu等linux系统上申请https证书
使用 Certbot 自动申请 安装 Certbot Certbot 是 Let’s Encrypt 官方推荐的自动化工具,支持多种操作系统和服务器环境。 在 Ubuntu/Debian 上: sudo apt update sudo apt install certbot申请证书 纯手动方式(不自动配置)&…...
