25寒假算法刷题 | Day1 | LeetCode 240. 搜索二维矩阵 II,148. 排序链表
目录
- 240. 搜索二维矩阵 II
- 题目描述
- 题解
- 148. 排序链表
- 题目描述
- 题解
240. 搜索二维矩阵 II
点此跳转题目链接
题目描述
编写一个高效的算法来搜索 m x n 矩阵 matrix 中的一个目标值 target 。该矩阵具有以下特性:
- 每行的元素从左到右升序排列。
- 每列的元素从上到下升序排列。
示例 1:

输入:matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 5
输出:true
示例 2:

输入:matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 20
输出:false
提示:
m == matrix.lengthn == matrix[i].length1 <= n, m <= 300-109 <= matrix[i][j] <= 109- 每行的所有元素从左到右升序排列
- 每列的所有元素从上到下升序排列
-109 <= target <= 109
题解
暴力算法直接遍历整个矩阵,时间复杂度为 O ( m n ) O(mn) O(mn) , m 、 n m、n m、n 分别为矩阵的行、列数。
由于题中矩阵在行和列上的元素都是升序的,所以想到可以从上到下逐行利用二分查找解决:
class Solution {
public:int binarySearch(const vector<int>& arr, int target) {int left = 0;int right = arr.size() - 1;while (left <= right) {int mid = left + (right - left) / 2;if (arr[mid] < target) {left = mid + 1;} else if (arr[mid] > target) {right = mid - 1;} else {return mid;}}return -1;}bool searchMatrix(vector<vector<int>>& matrix, int target) {if (matrix.empty()) {return false;}// 逐行使用二分法查找targetfor (const vector<int>& line : matrix) {if (binarySearch(line, target) != -1) {return true;}}return false;}
};
行内 n n n 个元素做二分查找的时间复杂度为 O ( l o g n ) O(logn) O(logn) ,共 m m m 行,故时间复杂度为 O ( m l o g n ) O(mlogn) O(mlogn) 。
不过上面两种方法似乎都过于直白简单了,考虑到这个题目带的是“中等”tag,肯定还有更高效的算法:
🔗 以下内容来自 LeetCode官方题解
我们可以从矩阵 matrix 的右上角 (0,n−1) 进行搜索。在每一步的搜索过程中,如果我们位于位置 (x,y) ,那么我们希望在以 matrix 的左下角为左下角、以 (x,y) 为右上角的矩阵中进行搜索,即行的范围为 [x,m−1] ,列的范围为 [0,y] :
- 如果
matrix[x,y]=target,说明搜索完成 - 如果
matrix[x,y]>target,由于每一列的元素都是升序排列的,那么在当前的搜索矩阵中,所有位于第y列的元素都是严格大于target的,因此我们可以将它们全部忽略,即将y减少 1 - 如果
matrix[x,y]<target,由于每一行的元素都是升序排列的,那么在当前的搜索矩阵中,所有位于第x行的元素都是严格小于target的,因此我们可以将它们全部忽略,即将x增加 1。
在搜索的过程中,如果我们超出了矩阵的边界,那么说明矩阵中不存在 target 。代码实现如下:
class Solution {
public:bool searchMatrix(vector<vector<int>>& matrix, int target) {int x = 0;int y = matrix[0].size() - 1;while (x < matrix.size() && y >= 0) {if (matrix[x][y] < target) {x++;} else if (matrix[x][y] > target) {y--;} else {return true;}}return false;}
};
时间复杂度: O ( m + n ) O(m+n) O(m+n) 。在搜索的过程中,如果我们没有找到 target ,那么我们要么将 y 减少 1,要么将 x 增加 1。由于 (x,y) 的初始值分别为 (0,n−1) ,因此 y 最多能被减少 n 次, x 最多能被增加 m 次,总搜索次数为 m+n 。在这之后, x 和 y 就会超出矩阵的边界。
148. 排序链表
点此跳转题目链接
题目描述
给你链表的头结点 head ,请将其按 升序 排列并返回 排序后的链表 。
示例 1:

输入:head = [4,2,1,3]
输出:[1,2,3,4]
示例 2:
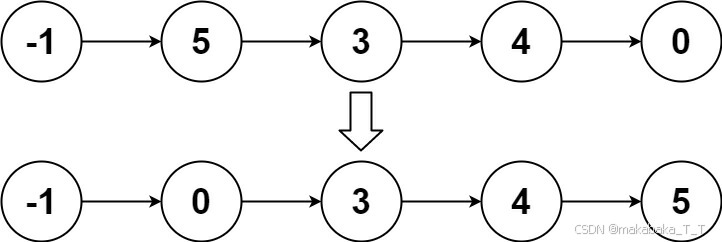
输入:head = [-1,5,3,4,0]
输出:[-1,0,3,4,5]
示例 3:
输入:head = []
输出:[]
提示:
- 链表中节点的数目在范围
[0, 5 * 104]内 -105 <= Node.val <= 105
进阶: 你可以在 O(n log n) 时间复杂度和常数级空间复杂度下,对链表进行排序吗?
题解
暴力解法无需多言,遍历一遍链表获取全部元素、排序后重新整一个新链表即可:
struct ListNode
{int val;ListNode *next;ListNode() : val(0), next(nullptr) {}ListNode(int x) : val(x), next(nullptr) {}ListNode(int x, ListNode *next) : val(x), next(next) {}
};class Solution {
public:ListNode* sortList(ListNode* head) {vector<int> elements;while (head){elements.push_back(head->val);head = head->next;}sort(elements.begin(), elements.end());ListNode *dummyHead = new ListNode();ListNode *cur = dummyHead;for (int element : elements) {cur->next = new ListNode(element);cur = cur->next;}return dummyHead->next;}
};
上述算法时间复杂度为 sort() 的 O ( n log n ) O(n\log{n}) O(nlogn) ,空间复杂度为 O ( n ) O(n) O(n) ——因为新建了一个链表。 直接看看进阶要求:时间复杂度为 O ( n log n ) O(n\log{n}) O(nlogn) ,空间复杂度为常数级。
考虑算法题中常用的高效排序算法——归并排序,有:
class Solution {
public:ListNode *merge(ListNode *L, ListNode *R) {ListNode dummyHead;ListNode *cur = &dummyHead;while (L && R) {if (L->val < R->val) {cur->next = L;L = L->next;} else {cur->next = R;R = R->next;}cur = cur->next;}cur->next = L ? L : R;return dummyHead.next;}ListNode *sortList(ListNode *head, ListNode *tail) {if (!head || head == tail) return head;// 快慢指针找到链表中点ListNode *slow = head, *fast = head;while (fast != tail && fast->next != tail) {slow = slow->next;fast = fast->next->next;}ListNode *mid = slow->next;slow->next = nullptr; // 断开链表return merge(sortList(head, slow), sortList(mid, tail));}ListNode *sortList(ListNode *head) { return sortList(head, nullptr); }
};
上述算法时间复杂度为 O ( n log n ) O(n\log{n}) O(nlogn) ,即归并排序的时间复杂度。空间复杂度取决于递归调用的栈空间,为 O ( log n ) O(\log{n}) O(logn) ,还是没到最佳的常数级别。为此,需要采用“自底向上”的归并排序实现 O ( 1 ) O(1) O(1) 的空间复杂度:
🔗 以下内容参考 LeetCode官方题解
首先求得链表的长度 length ,然后将链表拆分成子链表进行合并。具体做法如下:
- 用
subLength表示每次需要排序的子链表的长度,初始时subLength=1。 - 每次将链表拆分成若干个长度为
subLength的子链表(最后一个子链表的长度可以小于subLength),按照每两个子链表一组进行合并,合并后即可得到若干个长度为subLength×2的有序子链表(最后一个子链表的长度可以小于subLength×2)。合并两个子链表仍然使用之前用过的归并算法。 - 将
subLength的值加倍,重复第 2 步,对更长的有序子链表进行合并操作,直到有序子链表的长度大于或等于length,整个链表排序完毕。
通过数学归纳法易证最后得到的链表是有序的(每次合并用到的子链表是有序的,合并后的也是有序的)。
class Solution {
public:ListNode *merge(ListNode *L, ListNode *R) {ListNode dummyHead;ListNode *cur = &dummyHead;while (L && R) {if (L->val < R->val) {cur->next = L;L = L->next;} else {cur->next = R;R = R->next;}cur = cur->next;}cur->next = L ? L : R;return dummyHead.next;}ListNode *sortList(ListNode *head) {if (!head) {return nullptr;}// 获取链表长度int length = 0;ListNode *cur = head;while (cur != nullptr) {length++;cur = cur->next;}// 自底向上,两两合并长度为subLength的子链表ListNode *dummyHead = new ListNode(0, head);for (int subLength = 1; subLength < length; subLength <<= 1) {ListNode *prev = dummyHead;cur = prev->next;while (cur != nullptr) {// 获取第一个子链表ListNode *head1 = cur;for (int i = 1; i < subLength && cur->next != nullptr; ++i) {cur = cur->next;}// 获取第二个子链表ListNode *head2 = cur->next;cur->next = nullptr; // 断开第一个子链表结尾cur = head2;for (int i = 1; i < subLength && cur && cur->next; ++i) {cur = cur->next;}// 预存第三个子链表(即下一轮的第一个子链表)的头节点// 即第二个子链表结尾节点的next节点ListNode *nextHead = nullptr;if (cur != nullptr) {nextHead = cur->next;cur->next = nullptr; // 断开第二个子链表结尾}// 合并第一、二个子链表ListNode *merged = merge(head1, head2);// 更新prev、cur指针prev->next = merged;while (prev->next != nullptr) {prev = prev->next;}cur = nextHead;}}return dummyHead->next;}
};
该算法时间复杂度为 O ( n log n ) O(n \log{n}) O(nlogn) ,空间复杂度为 O ( 1 ) O(1) O(1) 。
相关文章:

25寒假算法刷题 | Day1 | LeetCode 240. 搜索二维矩阵 II,148. 排序链表
目录 240. 搜索二维矩阵 II题目描述题解 148. 排序链表题目描述题解 240. 搜索二维矩阵 II 点此跳转题目链接 题目描述 编写一个高效的算法来搜索 m x n 矩阵 matrix 中的一个目标值 target 。该矩阵具有以下特性: 每行的元素从左到右升序排列。每列的元素从上到…...
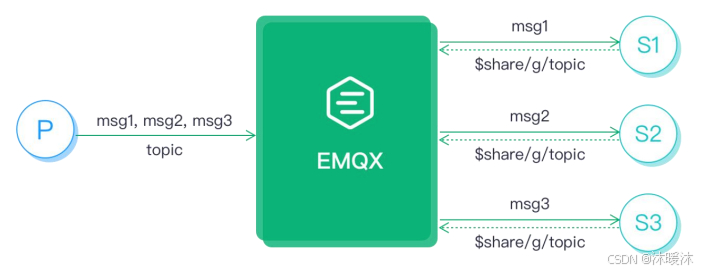
MQTT知识
MQTT协议 MQTT 是一种基于发布/订阅模式的轻量级消息传输协议,专门针对低带宽和不稳定网络环境的物联网应用而设计,可以用极少的代码为联网设备提供实时可靠的消息服务。MQTT 协议广泛应用于物联网、移动互联网、智能硬件、车联网、智慧城市、远程医疗、…...

【机器学习与数据挖掘实战】案例11:基于灰色预测和SVR的企业所得税预测分析
【作者主页】Francek Chen 【专栏介绍】 ⌈ ⌈ ⌈机器学习与数据挖掘实战 ⌋ ⌋ ⌋ 机器学习是人工智能的一个分支,专注于让计算机系统通过数据学习和改进。它利用统计和计算方法,使模型能够从数据中自动提取特征并做出预测或决策。数据挖掘则是从大型数据集中发现模式、关联…...

新一代搜索引擎,是 ES 的15倍?
Manticore Search介绍 Manticore Search 是一个使用 C 开发的高性能搜索引擎,创建于 2017 年,其前身是 Sphinx Search 。Manticore Search 充分利用了 Sphinx,显着改进了它的功能,修复了数百个错误,几乎完全重写了代码…...

使用 Context API 管理临时状态,避免 Redux/Zustand 的持久化陷阱
在开发 React Native 应用时,我们经常需要管理全局状态,比如用户信息、主题设置、网络状态等。而对于某些临时状态,例如 数据同步进行中的状态 (isSyncing),我们应该选择什么方式来管理它? 在项目开发过程中ÿ…...
PyTorch框架——基于深度学习YOLOv8神经网络学生课堂行为检测识别系统
基于YOLOv8深度学习的学生课堂行为检测识别系统,其能识别三种学生课堂行为:names: [举手, 读书, 写字] 具体图片见如下: 第一步:YOLOv8介绍 YOLOv8 是 ultralytics 公司在 2023 年 1月 10 号开源的 YOLOv5 的下一个重大更新版本…...

word2vec 实战应用介绍
Word2Vec 是一种由 Google 在 2013 年推出的重要词嵌入模型,通过将单词映射为低维向量,实现了对自然语言处理任务的高效支持。其核心思想是利用深度学习技术,通过训练大量文本数据,将单词表示为稠密的向量形式,从而捕捉单词之间的语义和语法关系。以下是关于 Word2Vec 实战…...

C# 操作符重载对象详解
.NET学习资料 .NET学习资料 .NET学习资料 一、操作符重载的概念 在 C# 中,操作符重载允许我们为自定义的类或结构体定义操作符的行为。通常,我们熟悉的操作符,如加法()、减法(-)、乘法&#…...

python学opencv|读取图像(五十四)使用cv2.blur()函数实现图像像素均值处理
【1】引言 前序学习进程中,对图像的操作均基于各个像素点上的BGR值不同而展开。 对于彩色图像,每个像素点上的BGR值为三个整数,因为是三通道图像;对于灰度图像,各个像素上的BGR值是一个整数,因为这是单通…...
: 非极大值抑制(Non-Maximum Suppression, NMS))
CNN的各种知识点(四): 非极大值抑制(Non-Maximum Suppression, NMS)
非极大值抑制(Non-Maximum Suppression, NMS) 1. 非极大值抑制(Non-Maximum Suppression, NMS)概念:算法步骤:具体例子:PyTorch实现: 总结: 1. 非极大值抑制(…...

虚幻基础16:locomotion direction
locomotion locomotion:角色运动系统的总称:包含移动、奔跑、跳跃、转向等。 locomotion direction 玩家输入 玩家输入:通常代表玩家想要的移动方向。 direction 可以计算当前朝向与移动方向的Δ。从而实现朝向与移动(玩家输入)方向的分…...

C++游戏开发实战:从引擎架构到物理碰撞
📝个人主页🌹:一ge科研小菜鸡-CSDN博客 🌹🌹期待您的关注 🌹🌹 1. 引言 C 是游戏开发中最受欢迎的编程语言之一,因其高性能、低延迟和强大的底层控制能力,被广泛用于游戏…...

代理模式——C++实现
目录 1. 代理模式简介 2. 代码示例 1. 代理模式简介 代理模式是一种行为型模式。 代理模式的定义:由于某些原因需要给某对象提供一个代理以控制该对象的访问。这时,访问对象不适合或者不能直接访问引用目标对象,代理对象作为访问对象和目标…...

什么情况下,C#需要手动进行资源分配和释放?什么又是非托管资源?
扩展:如何使用C#的using语句释放资源?什么是IDisposable接口?与垃圾回收有什么关系?-CSDN博客 托管资源的回收有GC自动触发,而非托管资源需要手动释放。 在 C# 中,非托管资源是指那些不由 CLR(…...

LeetCode 2909. 元素和最小的山形三元组 II
**### LeetCode 2909. 元素和最小的山形三元组 II 问题描述 给定一个下标从 0 开始的整数数组 nums,我们需要找到一个“山形三元组”(i, j, k)满足以下条件: i < j < knums[i] < nums[j] 且 nums[k] < nums[j] 并…...

搬迁至bilibili声明
我将搬迁到bilibili ,用户名:北苏清风 在这个用户名上的文章部分将出自csdn的这个账号,均属于本人原创...

【周易哲学】生辰八字入门讲解(八)
😊你好,我是小航,一个正在变秃、变强的文艺倾年。 🔔本文讲解【周易哲学】生辰八字入门讲解,期待与你一同探索、学习、进步,一起卷起来叭! 目录 一、六亲女命六亲星六亲宫位相互关系 男命六亲星…...

复制粘贴小工具——Ditto
在日常工作中,复制粘贴是常见的操作,但Windows系统自带的剪贴板功能较为有限,只能保存最近一次的复制记录,这对于需要频繁复制粘贴的用户来说不太方便。今天,我们介绍一款开源、免费且功能强大的剪贴板增强工具——Dit…...

3、从langchain到rag
文章目录 本文介绍向量和向量数据库向量向量数据库 索引开始动手实现rag加载文档数据并建立索引将向量存放到向量数据库中检索生成构成一条链 本文介绍 从本节开始,有了上一节的langchain基础学习,接下来使用langchain实现一个rag应用,并稍微…...

稀疏进化训练:机器学习优化算法中的高效解决方案
稀疏进化训练:机器学习优化算法中的高效解决方案 稀疏进化训练:机器学习优化算法中的高效解决方案引言第一部分:背景与动机1.1 传统优化算法的局限性1.2 进化策略的优势1.3 稀疏性的重要性 第二部分:稀疏进化训练的核心思想2.1 稀…...

LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器的上位机配置操作说明
LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器专为工业环境精心打造,完美适配AGV和无人叉车。同时,集成以太网与语音合成技术,为各类高级系统(如MES、调度系统、库位管理、立库等)提供高效便捷的语音交互体验。 L…...

web vue 项目 Docker化部署
Web 项目 Docker 化部署详细教程 目录 Web 项目 Docker 化部署概述Dockerfile 详解 构建阶段生产阶段 构建和运行 Docker 镜像 1. Web 项目 Docker 化部署概述 Docker 化部署的主要步骤分为以下几个阶段: 构建阶段(Build Stage):…...

深入剖析AI大模型:大模型时代的 Prompt 工程全解析
今天聊的内容,我认为是AI开发里面非常重要的内容。它在AI开发里无处不在,当你对 AI 助手说 "用李白的风格写一首关于人工智能的诗",或者让翻译模型 "将这段合同翻译成商务日语" 时,输入的这句话就是 Prompt。…...
使用rpicam-app通过网络流式传输视频)
树莓派超全系列教程文档--(62)使用rpicam-app通过网络流式传输视频
使用rpicam-app通过网络流式传输视频 使用 rpicam-app 通过网络流式传输视频UDPTCPRTSPlibavGStreamerRTPlibcamerasrc GStreamer 元素 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 使用 rpicam-app 通过网络流式传输视频 本节介绍来自 rpica…...

从WWDC看苹果产品发展的规律
WWDC 是苹果公司一年一度面向全球开发者的盛会,其主题演讲展现了苹果在产品设计、技术路线、用户体验和生态系统构建上的核心理念与演进脉络。我们借助 ChatGPT Deep Research 工具,对过去十年 WWDC 主题演讲内容进行了系统化分析,形成了这份…...

Go 语言接口详解
Go 语言接口详解 核心概念 接口定义 在 Go 语言中,接口是一种抽象类型,它定义了一组方法的集合: // 定义接口 type Shape interface {Area() float64Perimeter() float64 } 接口实现 Go 接口的实现是隐式的: // 矩形结构体…...

什么是库存周转?如何用进销存系统提高库存周转率?
你可能听说过这样一句话: “利润不是赚出来的,是管出来的。” 尤其是在制造业、批发零售、电商这类“货堆成山”的行业,很多企业看着销售不错,账上却没钱、利润也不见了,一翻库存才发现: 一堆卖不动的旧货…...

linux arm系统烧录
1、打开瑞芯微程序 2、按住linux arm 的 recover按键 插入电源 3、当瑞芯微检测到有设备 4、松开recover按键 5、选择升级固件 6、点击固件选择本地刷机的linux arm 镜像 7、点击升级 (忘了有没有这步了 估计有) 刷机程序 和 镜像 就不提供了。要刷的时…...

基于Docker Compose部署Java微服务项目
一. 创建根项目 根项目(父项目)主要用于依赖管理 一些需要注意的点: 打包方式需要为 pom<modules>里需要注册子模块不要引入maven的打包插件,否则打包时会出问题 <?xml version"1.0" encoding"UTF-8…...

Caliper 配置文件解析:config.yaml
Caliper 是一个区块链性能基准测试工具,用于评估不同区块链平台的性能。下面我将详细解释你提供的 fisco-bcos.json 文件结构,并说明它与 config.yaml 文件的关系。 fisco-bcos.json 文件解析 这个文件是针对 FISCO-BCOS 区块链网络的 Caliper 配置文件,主要包含以下几个部…...
