面试经典150题——栈
文章目录
- 1、有效的括号
- 1.1 题目链接
- 1.2 题目描述
- 1.3 解题代码
- 1.4 解题思路
- 2、
- 2.1 题目链接
- 2.2 题目描述
- 2.3 解题代码
- 2.4 解题思路
- 3、最小栈
- 3.1 题目链接
- 3.2 题目描述
- 3.3 解题代码
- 3.4 解题思路
- 4、逆波兰表达式求值
- 4.1 题目链接
- 4.2 题目描述
- 4.3 解题代码
- 4.4 解题思路
- 5、基本计算器
- 5.1 题目链接
- 5.2 题目描述
- 5.3 解题代码
- 5.4 解题思路
1、有效的括号
1.1 题目链接
点击跳转到题目位置
1.2 题目描述
给定一个只包括 ‘(’,‘)’,‘{’,‘}’,‘[’,‘]’ 的字符串 s ,判断字符串是否有效。
有效字符串需满足:
- 左括号必须用相同类型的右括号闭合。
- 左括号必须以正确的顺序闭合。
- 每个右括号都有一个对应的相同类型的左括号。
1.3 解题代码
class Solution {public boolean isValid(String s) {int n = s.length();if((n & 1) > 0){return false;}Stack<Character> stk = new Stack<>();for(int i = 0; i < n; ++i){char ch = s.charAt(i);if(stk.isEmpty()){stk.push(ch);continue;}char ch1 = stk.peek();if(ch == ')' && ch1 == '(' || ch == ']' && ch1 == '[' || ch == '}' && ch1 == '{'){stk.pop();} else if(ch == '(' || ch == '[' || ch == '{'){stk.push(ch);} else{return false;}}return stk.isEmpty();}
}
1.4 解题思路
- 栈的经典题目括号匹配问题。
- 如果栈为空则将括号压入数组中,如果栈顶元素和当前元素括号匹配,则出栈,否则入栈。
- 最后遍历完毕若栈为空则返回false,否则返回true。
2、
2.1 题目链接
点击跳转到题目位置
2.2 题目描述
给你一个字符串 path ,表示指向某一文件或目录的 Unix 风格 绝对路径 (以 ‘/’ 开头),请你将其转化为 更加简洁的规范路径。
在 Unix 风格的文件系统中规则如下:
- 一个点 ‘.’ 表示当前目录本身。
- 此外,两个点 ‘…’ 表示将目录切换到上一级(指向父目录)。
- 任意多个连续的斜杠(即,‘//’ 或 ‘///’)都被视为单个斜杠 ‘/’。
- 任何其他格式的点(例如,‘…’ 或 ‘…’)均被视为有效的文件/目录名称。
返回的 简化路径 必须遵循下述格式:
- 始终以斜杠 ‘/’ 开头。
- 两个目录名之间必须只有一个斜杠 ‘/’ 。
- 最后一个目录名(如果存在)不能 以 ‘/’ 结尾。
- 此外,路径仅包含从根目录到目标文件或目录的路径上的目录(即,不含 ‘.’ 或 ‘…’)。
返回简化后得到的 规范路径 。
提示:
- 1 <= path.length <= 3000
- path 由英文字母,数字,‘.’,‘/’ 或 ‘_’ 组成。
- path 是一个有效的 Unix 风格绝对路径。
2.3 解题代码
class Solution {public String simplifyPath(String path) {StringBuffer ret = new StringBuffer();Stack<String> stk = new Stack<>();StringBuffer sb = new StringBuffer();for(int i = 0; i < path.length(); ++i){if(path.charAt(i) == '/'){if(sb.length() != 0){stk.push(sb.toString());}sb.delete(0, sb.length());} else{sb.append(path.charAt(i));}}if(sb.length() > 0){stk.push(sb.toString());}List<String> temp = new ArrayList<String>();while(!stk.empty()){if(stk.peek().equals(".")){stk.pop();} else if(stk.peek().equals("..")){stk.pop();int num = 1;while(!stk.empty() && num > 0){if(stk.peek().equals(".")){stk.pop();continue;} else if(stk.peek().equals("..")){stk.pop();num++;} else{stk.pop();num--;}}} else{temp.add(stk.peek());stk.pop();}}int n = temp.size();for(int i = n - 1; i >= 0; --i){ret.append("/");ret.append(temp.get(i));}if(n == 0){ret.append("/");}return ret.toString();}
}
2.4 解题思路
- 先用字符串数组存储所有的字符串(以一个或多个‘/’分隔)。
- 接着用栈来去除掉所有多余的字符串,‘.’去除栈顶一个,‘…’去除栈顶两个,如果去除的有‘…’则需要再多去除一个。其他非上述的字符串则放入字符串数组中。
- 最后再逆序遍历该字符串数组,按照正确的格式拼接成一个字符串返回。
3、最小栈
3.1 题目链接
点击跳转到题目位置
3.2 题目描述
设计一个支持 push ,pop ,top 操作,并能在常数时间内检索到最小元素的栈。
实现 MinStack 类:
- MinStack() 初始化堆栈对象。
- void push(int val) 将元素val推入堆栈。
- void pop() 删除堆栈顶部的元素。
- int top() 获取堆栈顶部的元素。
- int getMin() 获取堆栈中的最小元素。
提示:
- -231 <= val <= 231 - 1
- pop、top 和 getMin 操作总是在 非空栈 上调用
- push, pop, top, and getMin最多被调用 3 * 104 次
3.3 解题代码
class MinStack {Stack<Integer> Min = new Stack<>();Stack<Integer> stk = new Stack<>();public MinStack() {while(!Min.empty()){Min.pop();}while(!stk.empty()){stk.pop();}}public void push(int val) {stk.push(val);if(Min.empty()){Min.push(val);} else{if(val < Min.peek()){Min.push(val);} else{Min.push(Min.peek());}}}public void pop() {stk.pop();Min.pop();}public int top() {return stk.peek();}public int getMin() {return Min.peek();}
}/*** Your MinStack object will be instantiated and called as such:* MinStack obj = new MinStack();* obj.push(val);* obj.pop();* int param_3 = obj.top();* int param_4 = obj.getMin();*/
3.4 解题思路
- 用一个栈正常进入入栈出栈操作。
- 维护一个最小栈,当栈顶为空的时候正常入栈,如果栈顶非空,如果当前栈中元素大于该元素则入最小栈,否则的话则将最小栈顶元素继续入栈。
4、逆波兰表达式求值
4.1 题目链接
点击跳转到题目位置
4.2 题目描述
给你一个字符串数组 tokens ,表示一个根据 逆波兰表示法 表示的算术表达式。
请你计算该表达式。返回一个表示表达式值的整数。
注意:
- 有效的算符为 ‘+’、‘-’、‘*’ 和 ‘/’ 。
- 每个操作数(运算对象)都可以是一个整数或者另一个表达式。
- 两个整数之间的除法总是 向零截断 。
- 表达式中不含除零运算。
- 输入是一个根据逆波兰表示法表示的算术表达式。
- 答案及所有中间计算结果可以用 32 位 整数表示。
提示:
1 <= tokens.length <= 104
tokens[i] 是一个算符(“+”、“-”、“*” 或 “/”),或是在范围 [-200, 200] 内的一个整数
逆波兰表达式:
逆波兰表达式是一种后缀表达式,所谓后缀就是指算符写在后面。
- 平常使用的算式则是一种中缀表达式,如 ( 1 + 2 ) * ( 3 + 4 ) 。
- 该算式的逆波兰表达式写法为 ( ( 1 2 + ) ( 3 4 + ) * ) 。
逆波兰表达式主要有以下两个优点:
去掉括号后表达式无歧义,上式即便写成 1 2 + 3 4 + * 也可以依据次序计算出正确结果。
- 适合用栈操作运算:遇到数字则入栈;
- 遇到算符则取出栈顶两个数字进行计算,并将结果压入栈中
4.3 解题代码
class Solution {int Alter(String s){int num = 0;if(s.charAt(0) >= '0' && s.charAt(0) <= '9'){for(int i = 0; i < s.length(); ++i){num *= 10;num += s.charAt(i) - '0';}} else{for(int i = 1; i < s.length(); ++i){num *= 10;num += s.charAt(i) - '0';}num *= -1;}return num;}int calculate(char ch, int num1, int num2){if(ch == '+'){return num2 + num1;} else if(ch == '-'){return num2 - num1;} else if(ch == '*'){return num2 * num1;} else if(ch == '/'){return num2 / num1;}return -1;}public int evalRPN(String[] tokens) {Stack<Integer> stk = new Stack<>();int n = tokens.length;for(int i = 0; i < n; ++i){String str = tokens[i];if(!str.equals("+") && !str.equals("-") && !str.equals("*") && !str.equals("/")){stk.push(Alter(str));} else{int num1 = stk.peek();stk.pop();int num2 = stk.peek();stk.pop();stk.push(calculate(str.charAt(0), num1, num2));}}return stk.peek();}
}
4.4 解题思路
- 用栈直接模拟逆波兰表达式的过程即可。
5、基本计算器
5.1 题目链接
点击跳转到题目位置
5.2 题目描述
给你一个字符串表达式 s ,请你实现一个基本计算器来计算并返回它的值。
注意:不允许使用任何将字符串作为数学表达式计算的内置函数,比如 eval() 。
提示:
- 1 <= s.length <= 3 * 105
- s 由数字、‘+’、‘-’、‘(’、‘)’、和 ’ ’ 组成
- s 表示一个有效的表达式
- ‘+’ 不能用作一元运算(例如, “+1” 和 “+(2 + 3)” 无效)
- ‘-’ 可以用作一元运算(即 “-1” 和 “-(2 + 3)” 是有效的)
- 输入中不存在两个连续的操作符
- 每个数字和运行的计算将适合于一个有符号的 32位 整数
5.3 解题代码
class Solution {public int calculate(String s) {int sum = 0;int i = 0;int n = s.length();Stack<Integer> stk = new Stack<>();int sign = 1;stk.push(1); // 一开始默认是加号while(i < n){char ch = s.charAt(i);if(ch == ' '){++i;} else if(ch == '+'){sign = stk.peek(); ++i;} else if(ch == '-'){sign = (stk.peek() * -1);++i;} else if(ch == '('){stk.push(sign);++i;} else if(ch == ')'){stk.pop();++i;} else{int num = 0;while(i < n && s.charAt(i) >= '0' && s.charAt(i) <= '9'){num *= 10;num += s.charAt(i) - '0';++i;}sum += sign * num;} }return sum;}
}
5.4 解题思路
- 首先往栈顶放入数字1,表示加号。
- 如果碰到‘+’则符号位设置为栈顶元素,如果碰到‘-’则符号位设置为栈顶元素 * -1,如果遇到左括号,则当前符号为负,则往栈顶元素放入-1,反之则为1,即当前存储的符号位。
- 从左往后每次遇到数字则结果加上符号位 * 数字即可。
相关文章:

面试经典150题——栈
文章目录 1、有效的括号1.1 题目链接1.2 题目描述1.3 解题代码1.4 解题思路 2、2.1 题目链接2.2 题目描述2.3 解题代码2.4 解题思路 3、最小栈3.1 题目链接3.2 题目描述3.3 解题代码3.4 解题思路 4、逆波兰表达式求值4.1 题目链接4.2 题目描述4.3 解题代码4.4 解题思路 5、基本…...

openmv的端口被拆分为两个 导致电脑无法访问openmv文件系统解决办法 openmv USB功能改动 openmv驱动被更改如何修复
我之前误打误撞遇到一次,直接把openmv的全部端口删除卸载然后重新插上就会自动重新装上一个openmv端口修复成功,大家可以先试试不行再用下面的方法 全部卸载再重新插拔openmv 要解决OpenMV IDE中出现的两个端口问题,可以尝试以下步骤&#x…...

自制虚拟机(C/C++)(三、做成标准GUI Windows软件,扩展指令集,直接支持img软盘)
开源地址:VMwork 要使终端不弹出, #pragma comment(linker, "/subsystem:windows /ENTRY:mainCRTStartup") 还要实现jmp near 0x01类似的 本次的main.cpp #include <graphics.h> #include <conio.h> #include <windows.h> #includ…...

算法题(56):旋转链表
审题: 我们需要根据k的大小把链表向右移动对应次数,并返回移动后的链表的头结点指针 思路: 根据提示中的数据大小我们发现:k的值可以远大于节点数。 也就是说我们对链表的操作存在周期,如果k%len0,说明我们…...

解决PyG安装中torch-sparse安装失败问题:详细指南
1 问题描述 最近在学习GNN,需要使用PyTorch Geometric(PyG)库。在安装PyG的过程中,遇到了torch-sparse安装失败的问题,错误提示为: ERROR: Failed building wheel for torch-sparse本文将详细记录问题的解…...

如何创建折叠式Title
文章目录 1 概念介绍2 使用方法3 示例代码 我们在上一章回中介绍了SliverGrid组件相关的内容,本章回中将介绍SliverAppBar组件.闲话休提,让我们一起Talk Flutter吧。 1 概念介绍 我们在本章回中介绍的SliverAppBar和普通的AppBar类似,它们的…...

go-zero学习笔记(三)
利用goctl生成rpc服务 编写proto文件 // 声明 proto 使用的语法版本 syntax "proto3";// proto 包名 package demoRpc;// golang 包名(可选) option go_package "./demo";// 如需为 .proto 文件添加注释,请使用 C/C 样式的 // 和 /* ... */…...

Wildcard工具详解:从入门到精通
1. Wildcard基础知识 什么是Wildcard? Wildcard(通配符)是一种用于匹配文件名或字符串的特殊字符。它允许用户使用简单的符号来表示复杂的匹配规则,从而快速定位目标文件或数据。 常见的Wildcard符号 *:匹配任意数量…...

冰蝎v3.0 beta7来啦
我用了一台kali,一台centos,一台windows,做了一个文件上传和一个反弹shell实验,载荷是AES加密的,终于感受到了对加密流量的无可奈何~ kali(php8.1)centos(php7.1)window…...

React中使用箭头函数定义事件处理程序
React中使用箭头函数定义事件处理程序 为什么使用箭头函数?1. 传递动态参数2. 避免闭包问题3. 确保每个方块的事件处理程序是独立的4. 代码可读性和维护性 示例代码总结 在React开发中,处理事件是一个常见的任务。特别是当我们需要传递动态参数时&#x…...

记忆化搜索和动态规划 --最长回文子串为例
记忆化搜索 记忆化搜索是一种优化递归算法的方法,通过将已经计算过的子问题的结果存储起来(通常使用哈希表或数组),避免重复计算相同的子问题。 本质上是通过缓存中间结果来减少计算的重复性。 动态规划 动态规划是通过将问题分…...
 ))
Tree Compass( Codeforces Round 934 (Div. 2) )
Tree Compass( Codeforces Round 934 (Div. 2) ) You are given a tree with n n n vertices numbered 1 , 2 , … , n 1, 2, \ldots, n 1,2,…,n. Initially, all vertices are colored white. You can perform the following two-step operation: …...

【Numpy核心编程攻略:Python数据处理、分析详解与科学计算】2.17 掩码数组:缺失值处理的优雅方案
2.17 掩码数组:缺失值处理的优雅方案 目录 #mermaid-svg-12vjJJbyudPnkYBO {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-12vjJJbyudPnkYBO .error-icon{fill:#552222;}#mermaid-svg-12vjJJbyudPnkYBO…...

PHP 常用函数2025.02
PHP implode() 函数 语法 implode(separator,array) 参数描述separator可选。规定数组元素之间放置的内容。默认是 ""(空字符串)。array必需。要组合为字符串的数组。 技术细节 返回值:返回一个由数组元素组合成的字符串。PHP 版…...

react中如何获取dom元素
实现代码 const inputRef useRef(null) inputRef.current.focus()...

【C++】继承(下)
大家好,我是苏貝,本篇博客带大家了解C的继承(下),如果你觉得我写的还不错的话,可以给我一个赞👍吗,感谢❤️ 目录 5.继承与友元6.继承与静态成员7.复杂的菱形继承及菱形虚拟继承8.继…...

C语言实现字符串排序:从代码到原理深度解析
在编程的世界里,字符串处理是一项基础且重要的技能。今天,我们通过分析一段C语言代码来深入了解如何对字符串进行排序。 一、代码呈现 #include <stdio.h> #include <string.h> int main() { char s[1001]; scanf("%s", s); int…...

Vue3的el-table-column下拉输入实时查询API数据选择的实现方法
由于本人对el-table-column有下拉输入选择的要求,根据网上搜索的资料及本人优化,推出我比较满意的方法,供各位读者参考使用。 效果图 el-table-column写法 <el-table-columnlabel"货品编号"align"center"prop"…...
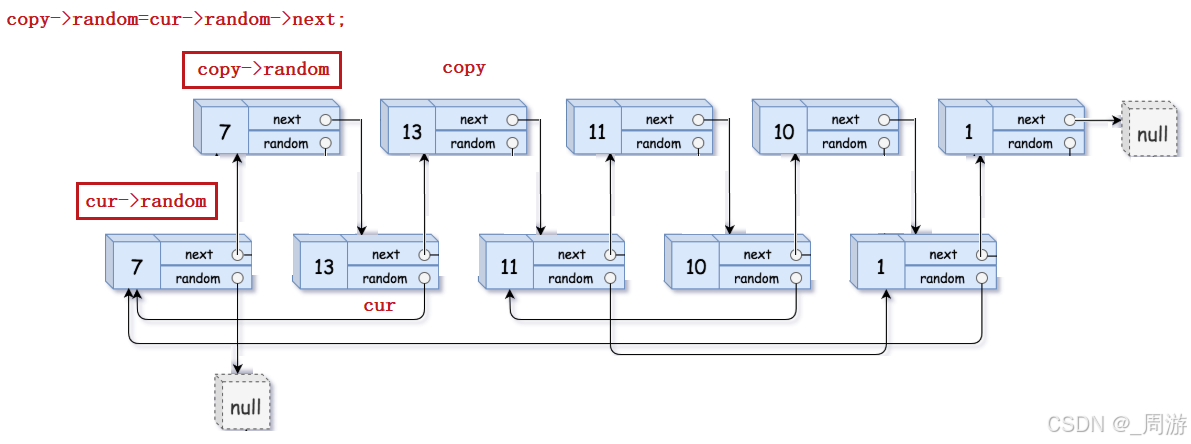
【数据结构】_链表经典算法OJ:复杂链表的复制
目录 1. 题目链接及描述 2. 解题思路 3. 程序 1. 题目链接及描述 题目链接:138. 随机链表的复制 - 力扣(LeetCode) 题目描述: 给你一个长度为 n 的链表,每个节点包含一个额外增加的随机指针 random ,…...

Vue 图片引用方式详解:静态资源与动态路径访问
目录 前言1. 引用 public/ 目录2. assets/ 目录3. 远程服务器4. Vue Router 动态访问5. 总结6. 扩展(图片不显示) 前言 🤟 找工作,来万码优才:👉 #小程序://万码优才/r6rqmzDaXpYkJZF 在 Vue 开发中&#x…...

Vim 调用外部命令学习笔记
Vim 外部命令集成完全指南 文章目录 Vim 外部命令集成完全指南核心概念理解命令语法解析语法对比 常用外部命令详解文本排序与去重文本筛选与搜索高级 grep 搜索技巧文本替换与编辑字符处理高级文本处理编程语言处理其他实用命令 范围操作示例指定行范围处理复合命令示例 实用技…...

黑马Mybatis
Mybatis 表现层:页面展示 业务层:逻辑处理 持久层:持久数据化保存 在这里插入图片描述 Mybatis快速入门 
多场景 OkHttpClient 管理器 - Android 网络通信解决方案
下面是一个完整的 Android 实现,展示如何创建和管理多个 OkHttpClient 实例,分别用于长连接、普通 HTTP 请求和文件下载场景。 <?xml version"1.0" encoding"utf-8"?> <LinearLayout xmlns:android"http://schemas…...
)
Java入门学习详细版(一)
大家好,Java 学习是一个系统学习的过程,核心原则就是“理论 实践 坚持”,并且需循序渐进,不可过于着急,本篇文章推出的这份详细入门学习资料将带大家从零基础开始,逐步掌握 Java 的核心概念和编程技能。 …...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现录音机应用
1. 项目配置与权限设置 1.1 配置module.json5 {"module": {"requestPermissions": [{"name": "ohos.permission.MICROPHONE","reason": "录音需要麦克风权限"},{"name": "ohos.permission.WRITE…...
可以参考以下方法:)
根据万维钢·精英日课6的内容,使用AI(2025)可以参考以下方法:
根据万维钢精英日课6的内容,使用AI(2025)可以参考以下方法: 四个洞见 模型已经比人聪明:以ChatGPT o3为代表的AI非常强大,能运用高级理论解释道理、引用最新学术论文,生成对顶尖科学家都有用的…...
)
GitHub 趋势日报 (2025年06月06日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 590 cognee 551 onlook 399 project-based-learning 348 build-your-own-x 320 ne…...

三分算法与DeepSeek辅助证明是单峰函数
前置 单峰函数有唯一的最大值,最大值左侧的数值严格单调递增,最大值右侧的数值严格单调递减。 单谷函数有唯一的最小值,最小值左侧的数值严格单调递减,最小值右侧的数值严格单调递增。 三分的本质 三分和二分一样都是通过不断缩…...

Web后端基础(基础知识)
BS架构:Browser/Server,浏览器/服务器架构模式。客户端只需要浏览器,应用程序的逻辑和数据都存储在服务端。 优点:维护方便缺点:体验一般 CS架构:Client/Server,客户端/服务器架构模式。需要单独…...

HubSpot推出与ChatGPT的深度集成引发兴奋与担忧
上周三,HubSpot宣布已构建与ChatGPT的深度集成,这一消息在HubSpot用户和营销技术观察者中引发了极大的兴奋,但同时也存在一些关于数据安全的担忧。 许多网络声音声称,这对SaaS应用程序和人工智能而言是一场范式转变。 但向任何技…...
