激活函数篇 03 —— ReLU、LeakyReLU、ELU
本篇文章收录于专栏【机器学习】
以下是激活函数系列的相关的所有内容:
一文搞懂激活函数在神经网络中的关键作用
逻辑回归:Sigmoid函数在分类问题中的应用
整流线性单位函数(Rectified Linear Unit, ReLU),又称修正线性单元,是一种人工神经网络中常用的激活函数,通常指代以斜坡函数及其变种为代表的非线性函数。
ReLU ( x ) = max ( 0 , x ) \text{ReLU}(x) = \max(0, x) ReLU(x)=max(0,x)
当输入 x > 0 x > 0 x>0 时,输出等于输入;当输入 x ≤ 0 x \leq 0 x≤0 时,输出为 0。

传统的激活函数如 Sigmoid 和 Tanh 存在梯度消失和计算效率较低的问题。ReLU 函数解决了这些问题,具有计算简单、不易出现梯度消失等特点。
应用场景
- 神经网络隐藏层:引入非线性,使网络能够学习复杂的特征表示。
- 输出层:在需要输出非负值的回归任务中使用。
- 特定任务:广泛应用于图像识别、自然语言处理等领域,如 CNN 和 RNN。
函数特点
- 控制输出范围:输出值限制在 [ 0 , ∞ ) [0, \infty) [0,∞),防止梯度消失或爆炸。
- 引入稀疏性:许多输出为零,减少模型复杂度,提高计算效率,防止过拟合。
- 提供可导性:其导数为:
ReLU ′ ( x ) = { 1 if x > 0 0 if x ≤ 0 \text{ReLU}'(x) = \begin{cases} 1 & \text{if } x > 0 \\ 0 & \text{if } x \leq 0 \end{cases} ReLU′(x)={10if x>0if x≤0
- 优点:
- 计算简单,计算效率高。
- 不易出现梯度消失问题。
- 引入稀疏性,有助于减少模型复杂度,提高计算效率,防止过拟合。
- 缺点:
- 神经元死亡:当 x ≤ 0 x \leq 0 x≤0 时,导数为 0,可能导致神经元死亡。
- 输出不以 0 为中心,可能影响梯度稳定性。
ReLU 函数的两个变体
Leaky ReLU:是 ReLU 的一个变体,在输入小于等于 0 时有一个小的非零斜率 α \alpha α,从而避免了神经元死亡问题:
Leaky ReLU ( x ) = { x if x > 0 α x if x ≤ 0 \text{Leaky ReLU}(x) = \begin{cases} x & \text{if } x > 0 \\ \alpha x & \text{if } x \leq 0 \end{cases} Leaky ReLU(x)={xαxif x>0if x≤0
α \alpha α 是一个小常数,通常取 0.01。在反向传播过程中,对于LeakyReLU激活函数输入小于 0 0 0 的部分,也可以计算得到梯度(ReLU的值为0),这样就避免了梯度方向锯齿问题。

ELU,即指数线性单元(Exponential Linear Unit),解决神经网络训练中的一些问题,如梯度消失、非连续性以及输出均值偏离零等问题。
理想的激活函数应满足两个条件:
- 输出的分布是零均值的,加快训练速度。
- 激活函数是单侧饱和的,更好的收敛。
LeakyReLU满足1不满足2;而ReLU满足2不满足1,ELU 都满足。
ELU:在 x ≤ 0 x \leq 0 x≤0 时有平滑的指数衰减,解决神经元死亡问题,数学表达式为:
ELU ( x ) = { x if x > 0 α ( e x − 1 ) if x ≤ 0 \text{ELU}(x) = \begin{cases} x & \text{if } x > 0 \\ \alpha (e^x - 1) & \text{if } x \leq 0 \end{cases} ELU(x)={xα(ex−1)if x>0if x≤0

特点
缓解梯度消失问题:当 ( x > 0 ),ELU 函数的行为类似于ReLU,允许直接传递输入,从而避免了梯度消失的问题。
对负值的处理更加温和:与ReLU不同的是,当 ( x < 0 ),ELU 不是简单地将它们置为0,而是通过指数函数给出一个非零的输出,这有助于保持网络中的信息流动。
输出的均值更接近于零:由于其在负区间内的特性,ELU 能够帮助神经网络学习到更具有鲁棒性的特征表示,并且倾向于产生更接近于零的输出均值,这对于加速学习过程是有益的。
ELU 的导数在 x > 0 x > 0 x>0 时为1,在 x < 0 x < 0 x<0 时为 α ⋅ e x \alpha \cdot e^x α⋅ex。特别地,在 x = 0 x = 0 x=0 处,通常认为其导数是连续的,取左侧或右侧极限值之一。
ELU 适用于需要减少偏移量并加快学习速度的任务,但计算上比ReLU稍微复杂一些,因为它涉及到指数运算。因此,在设计深度学习模型时,需权衡这些因素来决定最适合的激活函数。
相关文章:

激活函数篇 03 —— ReLU、LeakyReLU、ELU
本篇文章收录于专栏【机器学习】 以下是激活函数系列的相关的所有内容: 一文搞懂激活函数在神经网络中的关键作用 逻辑回归:Sigmoid函数在分类问题中的应用 整流线性单位函数(Rectified Linear Unit, ReLU),又称修正线性单元&a…...

山东大学软件学院人机交互期末复习笔记
文章目录 2022-2023 数媒方向2023-2024 软工方向重点题目绪论发展阶段 感知和认知基础视觉听觉肤觉知觉认知过程和交互设计原则感知和识别注意记忆问题解决语言处理影响认知的因素 立体显示技术及其应用红蓝眼镜偏振式眼镜主动式(快门时)立体眼镜 交互设…...

python 语音识别方案对比
目录 一、语音识别 二、代码实践 2.1 使用vosk三方库 2.2 使用SpeechRecognition 2.3 使用Whisper 一、语音识别 今天识别了别人做的这个app,觉得虽然是个日记app 但是用来学英语也挺好的,能进行语音识别,然后矫正语法,自己说的时候 ,实在不知道怎么说可以先乱说,然…...

docker常用命令及案例
以下是 Docker 的所有常用命令及其案例说明,按功能分类整理: 1. 镜像管理 1.1 拉取镜像 命令: docker pull <镜像名>:<标签>案例: 拉取官方的 nginx 镜像docker pull nginx:latest1.2 列出本地镜像 命令: docker images案例: 查看本地所有…...

DeepSeek-R1 云环境搭建部署流程
DeepSeek横空出世,在国际AI圈备受关注,作为个人开发者,AI的应用可以有效地提高个人开发效率。除此之外,DeepSeek的思考过程、思考能力是开放的,这对我们对结果调优有很好的帮助效果。 DeepSeek是一个基于人工智能技术…...

Java_双列集合
双列集合特点 存放的是键值对对象(Entry) Map 因为都是继承Map,所以要学会这些API,后面的类就都知道了 put 有两个操作,添加(并返回null)或者覆盖(返回被覆盖的值)…...

.net的一些知识点6
1.写个Lazy<T>的单例模式 public class SingleInstance{private static readonly Lazy<SingleInstance> instance new Lazy<SingleInstance>(() > new SingleInstance());private SingleInstance(){}public static SingleInstance Instace > instance…...

无须付费,安装即是完全版!
不知道大家有没有遇到过不小心删掉了电脑上超重要的文件,然后急得像热锅上的蚂蚁? 别担心,今天给大家带来一款超给力的数据恢复软件,简直就是拯救文件的“救星”! 数据恢复 专业的恢复数据软件 这款软件的界面设计得特…...

常见数据库对象与视图VIEW
常见的数据库对象 表 TABLE 数据字典 约束 CONSTRAINT 视图 VIEW 索引 INDEX 存储过程 PROCESS 存储函数 FUNCTION 触发器 TRIGGER 视图VIEW 1、引入 为什么使用视图? 视图可以帮助我们使用表的一部分,针对不同的用户制定不同的查询视图。 …...
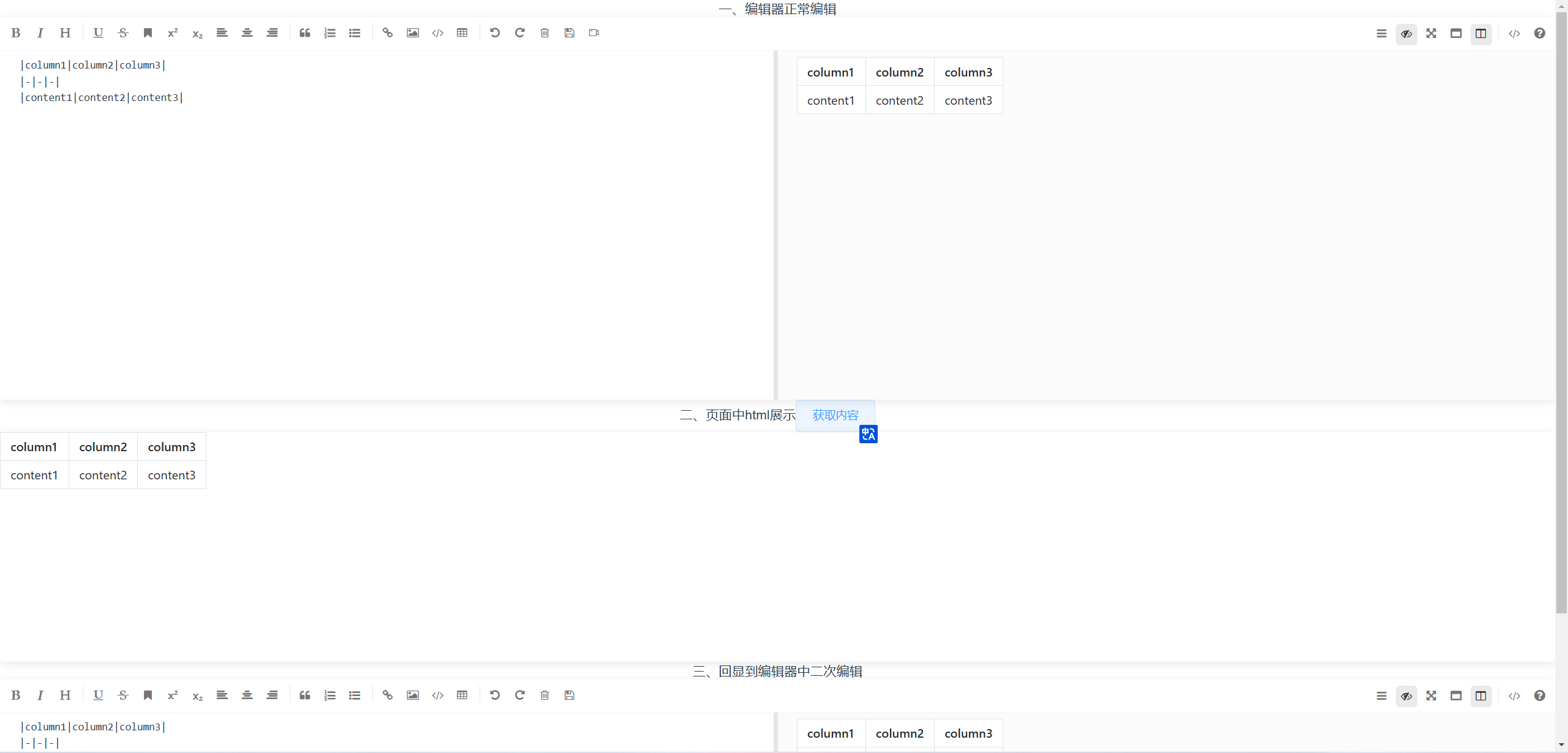
【Vue2】vue2项目中如何使用mavon-editor编辑器,数据如何回显到网页,如何回显到编辑器二次编辑
参考网站: 安装使用参考:vue2-常用富文本编辑器使用介绍 html网页展示、编辑器回显二次编辑参考:快速搞懂前端项目如何集成Markdown插件mavon-editor,并回显数据到网页 安装命令 npm install mavon-editor2.9.1 --save全局配置 …...

2、Python面试题解析:如何进行字符串插值?
Python字符串插值详解 字符串插值是将变量或表达式嵌入字符串中的一种技术,Python提供了多种方式实现字符串插值。以下是常见的几种方法及其详细解析和代码示例。 1. 百分号(%)格式化 这是Python早期版本中的字符串插值方法,类似…...

计算机网络-SSH基本原理
最近年底都在忙,然后这两天好点抽空更新一下。前面基本把常见的VPN都学习了一遍,后面的内容应该又继续深入一点。 一、SSH简介 SSH(Secure Shell,安全外壳协议)是一种用于在不安全网络上进行安全远程登录和实现其他安…...

doris:MySQL 兼容性
Doris 高度兼容 MySQL 语法,支持标准 SQL。但是 Doris 与 MySQL 还是有很多不同的地方,下面给出了它们的差异点介绍。 数据类型 数字类型 类型MySQLDorisBoolean- 支持 - 范围:0 代表 false,1 代表 true- 支持 - 关键字&am…...

mysql 存储过程和自定义函数 详解
首先创建存储过程或者自定义函数时,都要使用use database 切换到目标数据库,因为存储过程和自定义函数都是属于某个数据库的。 存储过程是一种预编译的 SQL 代码集合,封装在数据库对象中。以下是一些常见的存储过程的关键字: 存…...

C++ 中的 cJSON 解析库:用法、实现及递归解析算法与内存高效管理
在现代软件开发中,JSON(JavaScript Object Notation)作为一种轻量级的数据交换格式,因其易于阅读和编写、易于机器解析和生成的特性,被广泛应用于各种场景。C 作为一种强大的编程语言,自然也需要一个高效的…...

websocket自动重连封装
websocket自动重连封装 前端代码封装 import { ref, onUnmounted } from vue;interface WebSocketOptions {url: string;protocols?: string | string[];reconnectTimeout?: number; }class WebSocketService {private ws: WebSocket | null null;private callbacks: { [k…...

【C语言】球球大作战游戏
目录 1. 前期准备 2. 玩家操作 3. 生成地图 4. 敌人移动 5. 吃掉小球 6. 完整代码 1. 前期准备 游戏设定:小球的位置、小球的半径、以及小球的颜色 这里我们可以用一个结构体数组来存放这些要素,以方便初始化小球的信息。 struct Ball {int x;int y;float r;DWORD c…...

人工智能D* Lite 算法-动态障碍物处理、多步预测和启发式函数优化
在智能驾驶领域,D* Lite 算法是一种高效的动态路径规划算法,适用于处理环境变化时的路径重规划问题。以下将为你展示 D* Lite 算法的高级用法,包含动态障碍物处理、多步预测和启发式函数优化等方面的代码实现。 代码实现 import heapq impo…...

MySQL 8版本认证问题
目录 问题: Public Key Retrieval is not allowed原因: mysql 8.0 调整身份认证机制解决方法(三种) 问题: Public Key Retrieval is not allowed 连接MySQL8数据库的时候,报错内容如下:“Publi…...

Android 开发APP中参数配置与读取总结
以使用MQTT配置的参数 MQTT_BROKER_UR 、MQTT_USER_NAME、 MQTT_PASSWORD为例,说明配置设置和读取应用 项目中使用系统参数(如环境变量和gradle.properties文件中的属性)在Gradle构建脚本中,以下是一个详细的操作文档资料&…...

Admin.Net中的消息通信SignalR解释
定义集线器接口 IOnlineUserHub public interface IOnlineUserHub {/// 在线用户列表Task OnlineUserList(OnlineUserList context);/// 强制下线Task ForceOffline(object context);/// 发布站内消息Task PublicNotice(SysNotice context);/// 接收消息Task ReceiveMessage(…...

.Net框架,除了EF还有很多很多......
文章目录 1. 引言2. Dapper2.1 概述与设计原理2.2 核心功能与代码示例基本查询多映射查询存储过程调用 2.3 性能优化原理2.4 适用场景 3. NHibernate3.1 概述与架构设计3.2 映射配置示例Fluent映射XML映射 3.3 查询示例HQL查询Criteria APILINQ提供程序 3.4 高级特性3.5 适用场…...

PPT|230页| 制造集团企业供应链端到端的数字化解决方案:从需求到结算的全链路业务闭环构建
制造业采购供应链管理是企业运营的核心环节,供应链协同管理在供应链上下游企业之间建立紧密的合作关系,通过信息共享、资源整合、业务协同等方式,实现供应链的全面管理和优化,提高供应链的效率和透明度,降低供应链的成…...

前端导出带有合并单元格的列表
// 导出async function exportExcel(fileName "共识调整.xlsx") {// 所有数据const exportData await getAllMainData();// 表头内容let fitstTitleList [];const secondTitleList [];allColumns.value.forEach(column > {if (!column.children) {fitstTitleL…...

pikachu靶场通关笔记22-1 SQL注入05-1-insert注入(报错法)
目录 一、SQL注入 二、insert注入 三、报错型注入 四、updatexml函数 五、源码审计 六、insert渗透实战 1、渗透准备 2、获取数据库名database 3、获取表名table 4、获取列名column 5、获取字段 本系列为通过《pikachu靶场通关笔记》的SQL注入关卡(共10关࿰…...

Xen Server服务器释放磁盘空间
disk.sh #!/bin/bashcd /run/sr-mount/e54f0646-ae11-0457-b64f-eba4673b824c # 全部虚拟机物理磁盘文件存储 a$(ls -l | awk {print $NF} | cut -d. -f1) # 使用中的虚拟机物理磁盘文件 b$(xe vm-disk-list --multiple | grep uuid | awk {print $NF})printf "%s\n"…...

【生成模型】视频生成论文调研
工作清单 上游应用方向:控制、速度、时长、高动态、多主体驱动 类型工作基础模型WAN / WAN-VACE / HunyuanVideo控制条件轨迹控制ATI~镜头控制ReCamMaster~多主体驱动Phantom~音频驱动Let Them Talk: Audio-Driven Multi-Person Conversational Video Generation速…...

基于Java+MySQL实现(GUI)客户管理系统
客户资料管理系统的设计与实现 第一章 需求分析 1.1 需求总体介绍 本项目为了方便维护客户信息为了方便维护客户信息,对客户进行统一管理,可以把所有客户信息录入系统,进行维护和统计功能。可通过文件的方式保存相关录入数据,对…...

云原生安全实战:API网关Kong的鉴权与限流详解
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 一、基础概念 1. API网关(API Gateway) API网关是微服务架构中的核心组件,负责统一管理所有API的流量入口。它像一座…...

解读《网络安全法》最新修订,把握网络安全新趋势
《网络安全法》自2017年施行以来,在维护网络空间安全方面发挥了重要作用。但随着网络环境的日益复杂,网络攻击、数据泄露等事件频发,现行法律已难以完全适应新的风险挑战。 2025年3月28日,国家网信办会同相关部门起草了《网络安全…...
