C++数据结构 —— 二叉搜索树
目录
1.二叉搜索树的基本概念
1.1二叉搜索树的基本特征
2.二叉搜索树的实现
2.1数据的插入(迭代实现)
2.2数据的搜索(迭代实现)
2.3中序遍历(递归实现)
2.4数据的删除(迭代实现)
2.5数据的搜索(递归实现)
2.6数据的插入(递归实现)
2.7数据的删除(递归实现)
2.8类的完善
3.二叉搜索树的应用
4.完整代码
二叉搜索树
1.二叉搜索树的基本概念
二叉搜索树又称二叉排序树,它可以是一颗空树。二叉搜索树的作用是搜索,排序(二叉搜索树的中序遍历是一组递增有序数据)。
1.1二叉搜索树的基本特征
如果某颗二叉树(包括空树)满足以下性质,可以作为一颗二叉搜索树:
1.如果左子树不为空,其键值应小于根节点的键值。
2.如果右子树不为空,其键值应大于根节点的键值。
3.左右子树都满足上述条件。
没有二叉搜索树之前,常用的查找算法为二分查找。但是二分查找是有局限性的(必须针对有序数组)。二叉搜索树因其特性,例如我们需要查找Key值,只需要与根节点的键值做比较:若Key小于根节点的键值,则往根节点的左子树遍历;若Key值大于根节点的键值,则往根节点的右子树遍历。经计算,查找的次数等于二叉搜索树的深度。正因为如此,二叉搜索树并不是一个优秀的数据结构,因为一但碰到极端情况,二叉搜索树的搜索效率将会大打折扣。所以在往后的章节中,将会使其平衡。

2.二叉搜索树的实现
将二叉搜索树定义为一个类,现在将展示类的框架。往后所有的演示代码,都可以直接加入其中:
// 节点
template <class K>
struct BST_node
{BST_node<K>* _left; //左子树BST_node<K>* _right; //右子树K _key;BST_node(const K& _key):_key(key),_left(nullptr),_right(nullptr){}
};template <class K> //节点键值的数据类型
class BST
{typedef BST_node<K> Node;
public:private:Node* _root; //根节点
};2.1数据的插入(迭代实现)
bool insert(const K& key)
{if (_root == nullptr){_root = new Node(key);return true;}Node* prev = nullptr; // cur的父节点Node* cur = _root;while (cur){if (key < cur->_key) //如果比根节点的键值小{prev = cur;cur = cur->_left;}else if(key > cur->_key) //如果比根节点的键值大{prev = cur;cur = cur->_right;}else{// 我们不允许插入重复的数据return false;}}// 直到遍历到空,才施行插入cur = new Node(key);if (key < prev->_key){prev->_left = cur;}else if (key > prev->_key){prev->_right = cur;}return true;
}2.2数据的搜索(迭代实现)
bool find(const K& key)
{if (_root == nullptr){return false;}Node* cur = _root;while (cur){if (key < cur->_key){cur = cur->_left;}else if (key > cur->_key){cur = cur->_right;}else{// 找到了return true;}}return false;
}2.3中序遍历(递归实现)
void MidTraval() //此接口作公有
{__MidTraval(_root);cout << endl;
}void __MidTraval(Node* root) //此接口做私有
{if (root == nullptr){return;}__MidTraval(root->_left);cout << root->_key << " ";__MidTraval(root->_right);
}2.4数据的删除(迭代实现)
需要注意,要删除二叉搜索树的节点,就必须分两种情况讨论:
1.要删除节点的左子树或右子树为空。
2.要删除节点的左、右子树都不为空。

bool erase(const K& key)
{if (_root == nullptr){return false;}Node* prev = _root;Node* cur = _root;while (cur){if (key < cur->_key){prev = cur;cur = cur->_left;}else if (key > cur->_key){prev = cur;cur = cur->_right;}else{// 如果左子树为空if (cur->_left == nullptr){// 假设右子树不为空,则将右子树托孤给父节点if (_root == cur){_root = _root->_right;}else if (prev->_left == cur){prev->_left = cur->_right;}else if (prev->_right == cur){prev->_right = cur->_right;}delete cur;return true;}// 如果右子树为空else if (cur->_right == nullptr){//假设左子树不为空,则将左子树托孤给父节点if (_root == cur){_root = _root->_left;}else if (prev->_left == cur){prev->_left = cur->_left;}else if (prev->_right == cur){prev->_right = cur->_left;}delete cur;return true;}// 如果左右子树都不为空else{// 假设使用右子树的最小值替代Node* prev = _root;Node* minRight = cur->_right;while (minRight->_left) //二叉树特性,越往左越小{prev = minRight;minRight = minRight->_left;}cur->_key = minRight->_key;// 替换好后,就要删除minRightif (prev->_left == minRight){prev->_left = minRight->_right;}else if (prev->_right == minRight){prev->_right = minRight->_right;}delete minRight;return true;}}}return false;
}2.5数据的搜索(递归实现)
bool findR(const K& key)
{return __findR(_root, key);
}bool __findR(Node* root, const K& key) //此接口作私有
{if (root == nullptr){return false;}if (key < root->_key){return __findR(root->_left, key);}else if (key > root->_key){return __findR(root->_right, key);}return true;
}2.6数据的插入(递归实现)
bool insertR(const K& key)
{return __insertR(_root, key);
}bool __insertR(Node*& root, const K& key) //此接口作私有
{if (root == nullptr){root = new Node(key); //注意引用传参,root相当于root->left或root->right的别名return true;}if (key < root->_key){return __insertR(root->_left, key);}else if (key > root->_key){return __insertR(root->_right, key);}return false;
}2.7数据的删除(递归实现)
bool eraseR(const K& key)
{return __eraseR(_root, key);
}bool __eraseR(Node*& root, const K& key) //此接口作私有
{if (root == nullptr){return false;}if (key < root->_key){return __eraseR(root->_left, key);}else if (key > root->_key){return __eraseR(root->_right, key);}else{Node* del = root;if (root->_left == nullptr){// 此时root就是要删除的节点,并且是root的父节点的子节点的引用(root == root->_left...)root = root->_right;delete del;return true;}else if (root->_right == nullptr){root = root->_left;delete del;return true;}else{Node* prev = _root;Node* minRight = root->_right;while (minRight->_left) //二叉树特性,越往左越小{prev = minRight;minRight = minRight->_left;}root->_key = minRight->_key;// 替换好后,就要删除minRightif (prev->_left == minRight){prev->_left = minRight->_right;}else if (prev->_right == minRight){prev->_right = minRight->_right;}delete minRight;return true;}}return false;
}2.8类的完善
BST():_root(nullptr)
{}~BST()
{Destructor(_root);_root = nullptr;
}void Destructor(Node* root) //此函数作私有
{if (root == nullptr){return;}// 后序删除Destructor(root->_left);Destructor(root->_right);delete root;
}BST(const BST<K>& t)
{_root = Copy(t._root);
}Node* Copy(Node* root) //此接口作私有
{if (root == nullptr){return nullptr;}Node* ret = new Node(root->_key);ret->_left = Copy(root->_left);ret->_right = Copy(root->_right);return ret;
}BST<K>& operator==(BST<K> t) //现代写法
{swap(_root, t._root);return *this;
}3.二叉搜索树的应用
1.K模型:
K模型即只有key作为关键码,结构中只需要存储Key即可,关键码即为需要搜索到的值。上面模拟实现的搜索就是K模型。
例如将英文字典所有的英文单词存储二叉搜索树这个数据结构,那么可将英文单词看作关键码Key,假设我们想查找"hello"这个单词,直接去数据结构找即可。
2.KV模型:
每一个关键码key,都有与之对应的值Value,即<Key, Value>的键值对。该种方式在现实生活中非常常见。
例如英汉互译,一个英文单词对应了多个汉语翻译。我们将<英文单词,中文翻译的数组>这样的键值对放入二叉搜索树中。例如查找"hello"这个单词的中文翻译,只需要查找键值对的英文单词即可。
KV模型例题:
给定下面数组,求每种水果出现的次数:
string arr[] = { "苹果", "西瓜", "苹果", "西瓜", "苹果", "苹果", "西瓜", "苹果", "香蕉", "苹果", "香蕉" };第一步:先实现二叉搜索树(为了方便,这里只保留插入数据、查找和中序遍历的接口):
namespace KV {// 节点template <class Key,class Val>struct BST_node{BST_node<Key,Val>* _left; //左子树BST_node<Key,Val>* _right; //右子树Key _key;Val _val;BST_node(const Key& key,const Val& val):_key(key), _val(val),_left(nullptr), _right(nullptr){}};template <class Key,class Val>class BST{typedef BST_node<Key,Val> Node;public:bool insert(const Key& key,const Val& val){if (_root == nullptr){_root = new Node(key,val);return true;}Node* prev = nullptr;Node* cur = _root;while (cur){if (key < cur->_key){prev = cur;cur = cur->_left;}else if (key > cur->_key){prev = cur;cur = cur->_right;}else{return false;}}cur = new Node(key,val);if (key < prev->_key){prev->_left = cur;}else if (key > prev->_key){prev->_right = cur;}return true;}Node* find(const Key& key){if (_root == nullptr){return nullptr;}Node* cur = _root;while (cur){if (key < cur->_key){cur = cur->_left;}else if (key > cur->_key){cur = cur->_right;}else{// 找到了return cur;}}return nullptr;}bool erase(const Key& key){if (_root == nullptr){return false;}Node* prev = _root;Node* cur = _root;while (cur){if (key < cur->_key){prev = cur;cur = cur->_left;}else if (key > cur->_key){prev = cur;cur = cur->_right;}else{if (cur->_left == nullptr){if (_root == cur){_root = _root->_right;}else if (prev->_left == cur){prev->_left = cur->_right;}else if (prev->_right == cur){prev->_right = cur->_right;}delete cur;return true;}else if (cur->_right == nullptr){if (_root == cur){_root = _root->_left;}else if (prev->_left == cur){prev->_left = cur->_left;}else if (prev->_right == cur){prev->_right = cur->_left;}delete cur;return true;}else{Node* prev = _root;Node* minRight = cur->_right;while (minRight->_left){prev = minRight;minRight = minRight->_left;}cur->_key = minRight->_key;if (prev->_left == minRight){prev->_left = minRight->_right;}else if (prev->_right == minRight){prev->_right = minRight->_right;}delete minRight;return true;}}}return false;}void MidTraval() {__MidTraval(_root);cout << endl;}private:Node* _root = nullptr;void __MidTraval(Node* root){if (root == nullptr){return;}__MidTraval(root->_left);cout << root->_key << ":" << root->_val << endl;__MidTraval(root->_right);}}; }第二步:算法实现:
void test_count() {KV::BST<string, int> bt;string arr[] = { "苹果", "西瓜", "苹果", "西瓜", "苹果", "苹果", "西瓜", "苹果", "香蕉", "苹果", "香蕉" };for (auto& e : arr){KV::BST_node<string, int>* ret = bt.find(e);if (ret) //不为空,证明数据结构已有{ret->_val++; //次数++}else{bt.insert(e, 1);}}bt.MidTraval(); }
4.完整代码
二叉搜索树
相关文章:

C++数据结构 —— 二叉搜索树
目录 1.二叉搜索树的基本概念 1.1二叉搜索树的基本特征 2.二叉搜索树的实现 2.1数据的插入(迭代实现) 2.2数据的搜索(迭代实现) 2.3中序遍历(递归实现) 2.4数据的删除(迭代实现) 2.5数据的搜索(递归实现) 2.6数据的插入(递归实现) 2.7数据的删除(递归实现) 2.8类的完…...

Maven面试题及答案
1、Maven有哪些优点和缺点 优点: 1、简化项目依赖管理 2、方便与持续集成工具(Jenkins)整合 3、有助于多模块项目开发,比如一个模块开发好后发布到仓库,依赖该模块时可以直接从远程仓库更新,不用自己手动去编译 4、有很多插件&am…...

WebRTC系列-Qos系列之接收放RTX处理
文章目录 1. RTX详解1.1 RTX包头解析1.2 RTX包中的OSN2. RTX在WebRTC中处理2.1 组包2.2 解包2.3 发送及接收处理流程2.3.1 发送流程2.3.2 rtx标记的设置流程2.3.3 解析流程2.3.4 RTX解包在上一篇 WebRTC系列-Qos系列之接收NACK文章中分析了接收到nack后解析的主要流程。在WebR…...

国内能否炒伦敦金,2023国际十大正规伦敦金交易平台排名
在目前的投资市场环境中,现货黄金是一种屡见不鲜的投资选择,它依靠国际化的投资环境,成为了世界范围内投资者的重要选择对象。进行现货黄金投资,人们除了要认识市场发展基本现状之外,更要做好基本面和技术面分析工作&a…...

react路由 - react-router-dom
react路由 现代的前端应用大多都是 SPA(单页应用程序),也就是只有一个 HTML 页面的应用程序。因为它的用户体验更好、对服务器的压力更小,所以更受欢迎。为了有效的使用单个页面来管理原来多页面的功能,前端路由应运而…...
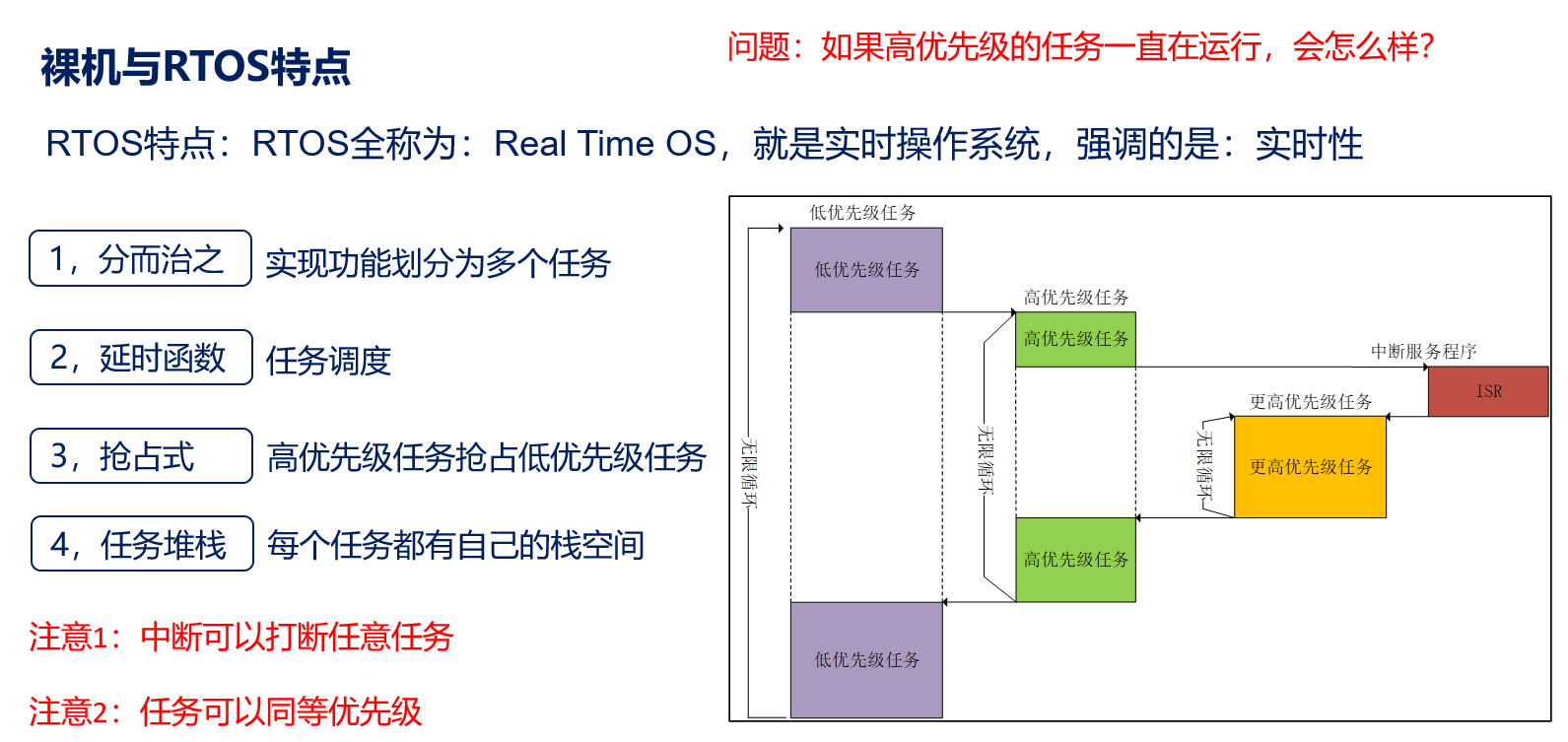
01-RTOS
对于裸机而言,对于RTOS而言即:对于裸机,打游戏意味着不能回消息 回消息意味着不能打游戏对于RTOS 打游戏和裸机的切换只需要一个时间片节拍 1ms 从宏观来看 就是同时进行的两件事(但要在这两件事情的优先级一样的情况下࿰…...

信息安全管理
信息安全管理信息安全管理信息安全风险管理信息安全管理体系应急响应与灾难恢复应急响应概况信息系统灾难修复灾难恢复相关技术信息安全管理 管理概念:组织、协调、控制的活动,核心过程的管理控制 管理对象和组成:包括人员在内相关资产&…...

深度学习tips
1、datasets_make函数中最后全部转化为numpy形式 datanp.array(data)否则会出现问题,比如数据是103216,经过trainloader生成tensor后(batch_size为30),发现生成的数据为: data.shape #(10,) data[0].shape…...

2023-2-13 刷题情况
替换子串得到平衡字符串 题目描述 有一个只含有 ‘Q’, ‘W’, ‘E’, ‘R’ 四种字符,且长度为 n 的字符串。 假如在该字符串中,这四个字符都恰好出现 n/4 次,那么它就是一个「平衡字符串」。 给你一个这样的字符串 s,请通过…...
[HSCSEC 2023] rev,pwn,crypto,Ancient-MISC部分
比赛后有讲解,没赶上,前20比赛完1小时提交WP,谁会大半夜的起来写WP。总的感觉pwn,crypto过于简单,rev有2个难的不会,其它不是我的方向都感觉过于难,一个都没作。revDECOMPILEONEOONE入门题,一个…...

SpringBoot 接入 Spark
本文主要介绍 SpringBoot 与 Spark 如何对接,具体使用可以参考文章 SpringBoot 使用 Spark pom 文件添加 maven 依赖 spark-core:spark 的核心库,如:SparkConfspark-sql:spark 的 sql 库,如:s…...

在线支付系列【23】支付宝开放平台产品介绍
有道无术,术尚可求,有术无道,止于术。 文章目录前言支付产品App 支付手机网站支付电脑网站支付新当面资金授权当面付营销产品营销活动送红包会员产品App 支付宝登录人脸认证信用产品芝麻 GO芝麻先享芝麻免押芝麻工作证安全产品交易安全防护其…...
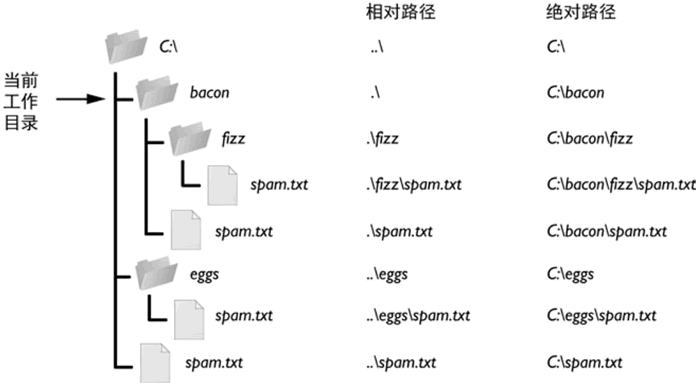
Python绝对路径和相对路径详解
在介绍绝对路径和相对路径之前,先要了解一下什么是当前工作目录。什么是当前工作目录每个运行在计算机上的程序,都有一个“当前工作目录”(或 cwd)。所有没有从根文件夹开始的文件名或路径,都假定在当前工作目录下。注…...

基于多进程的并发编程
一:不同平台基于多进程并发编程的实现 1.Windows平台 参考博文:Windows 编程(多进程) 更多API: 1)waitForSingleObject:等待一个内核对象变为已通知状态 2)GetExitCodeProcess:获取…...
:CBV和FBV)
Flask入门(4):CBV和FBV
目录4.CBV和FBV4.1 继承 views.View4.2 继承 views.MethodView4.CBV和FBV 前面的例子中,都是基于视图函数构建视图(FBV),和Django一样,Flask也有基于类构建视图(CBV)的方法。这种方式用的不多&…...
Qt OpenGL(三十九)——Qt OpenGL 核心模式-在雷达坐标系中绘制飞行的飞机
提示:本系列文章的索引目录在下面文章的链接里(点击下面可以跳转查看): Qt OpenGL 核心模式版本文章目录 Qt OpenGL(三十九)——Qt OpenGL 核心模式-在雷达坐标系中绘制飞行的飞机 一、场景 在之前绘制完毕雷达显示图之后,这时候,我们能匹配的场景就更广泛了,比如说…...

系统应用 odex 转 dex
说下为什会有这个需求,以某系统应用为例,我们通过 adb 获取到的 apk 反编译查看只有少部分代码和资源,关键代码看不到。 经过一系列操作,把 odex 转换为 dex 可以看到源码。 工具下载 Smali 下载 1、使用 adb shell pm list pa…...
【GPLT 三阶题目集】L3-013 非常弹的球
刚上高一的森森为了学好物理,买了一个“非常弹”的球。虽然说是非常弹的球,其实也就是一般的弹力球而已。森森玩了一会儿弹力球后突然想到,假如他在地上用力弹球,球最远能弹到多远去呢?他不太会,你能帮他解…...
vue项目第三天
论坛项目动态路由菜单以及渲染用户登录全局前置拦截器获取用户的菜单以及接口执行过程解析菜单数据,渲染伟动态路由。菜单数据将数据源解析为类似路由配置对象的格式(./xxx/xxx 这种格式)。下方是路由实例的代码,后面封装了很多方法这里也需要…...
【渝偲医药】实验室关于核磁共振波谱NMR的知识(原理、用途、分析、问题)
核磁共振波谱法(Nuclear Magnetic Resonance,简写为NMR)与紫外吸收光谱、红外吸收光谱、质谱被人们称为“四谱",是对各种有机和无机物的成分、结构进行定性分析的强有力的工具之一,亦可进行定量分析。 核磁共振&…...
详解)
后进先出(LIFO)详解
LIFO 是 Last In, First Out 的缩写,中文译为后进先出。这是一种数据结构的工作原则,类似于一摞盘子或一叠书本: 最后放进去的元素最先出来 -想象往筒状容器里放盘子: (1)你放进的最后一个盘子(…...

利用ngx_stream_return_module构建简易 TCP/UDP 响应网关
一、模块概述 ngx_stream_return_module 提供了一个极简的指令: return <value>;在收到客户端连接后,立即将 <value> 写回并关闭连接。<value> 支持内嵌文本和内置变量(如 $time_iso8601、$remote_addr 等)&a…...

通过Wrangler CLI在worker中创建数据库和表
官方使用文档:Getting started Cloudflare D1 docs 创建数据库 在命令行中执行完成之后,会在本地和远程创建数据库: npx wranglerlatest d1 create prod-d1-tutorial 在cf中就可以看到数据库: 现在,您的Cloudfla…...

基于服务器使用 apt 安装、配置 Nginx
🧾 一、查看可安装的 Nginx 版本 首先,你可以运行以下命令查看可用版本: apt-cache madison nginx-core输出示例: nginx-core | 1.18.0-6ubuntu14.6 | http://archive.ubuntu.com/ubuntu focal-updates/main amd64 Packages ng…...

从深圳崛起的“机器之眼”:赴港乐动机器人的万亿赛道赶考路
进入2025年以来,尽管围绕人形机器人、具身智能等机器人赛道的质疑声不断,但全球市场热度依然高涨,入局者持续增加。 以国内市场为例,天眼查专业版数据显示,截至5月底,我国现存在业、存续状态的机器人相关企…...

【解密LSTM、GRU如何解决传统RNN梯度消失问题】
解密LSTM与GRU:如何让RNN变得更聪明? 在深度学习的世界里,循环神经网络(RNN)以其卓越的序列数据处理能力广泛应用于自然语言处理、时间序列预测等领域。然而,传统RNN存在的一个严重问题——梯度消失&#…...

【第二十一章 SDIO接口(SDIO)】
第二十一章 SDIO接口 目录 第二十一章 SDIO接口(SDIO) 1 SDIO 主要功能 2 SDIO 总线拓扑 3 SDIO 功能描述 3.1 SDIO 适配器 3.2 SDIOAHB 接口 4 卡功能描述 4.1 卡识别模式 4.2 卡复位 4.3 操作电压范围确认 4.4 卡识别过程 4.5 写数据块 4.6 读数据块 4.7 数据流…...
【机器视觉】单目测距——运动结构恢复
ps:图是随便找的,为了凑个封面 前言 在前面对光流法进行进一步改进,希望将2D光流推广至3D场景流时,发现2D转3D过程中存在尺度歧义问题,需要补全摄像头拍摄图像中缺失的深度信息,否则解空间不收敛…...

376. Wiggle Subsequence
376. Wiggle Subsequence 代码 class Solution { public:int wiggleMaxLength(vector<int>& nums) {int n nums.size();int res 1;int prediff 0;int curdiff 0;for(int i 0;i < n-1;i){curdiff nums[i1] - nums[i];if( (prediff > 0 && curdif…...

Java-41 深入浅出 Spring - 声明式事务的支持 事务配置 XML模式 XML+注解模式
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...
