C++广度优先搜索
简介
老规矩,先来介绍一下什么是广度优先搜索(至于这么长时间没更新是为什么,我放在文章结尾了,感兴趣可以看看,以后也是如此)
广度优先搜索,从名字就能听出来,他和深度优先搜索关系匪浅,没错,他们是“孪生兄弟”。两者虽然是“孪生兄弟”但差别可是巨大无比:一个会深入每一条路径,也就是“不撞南墙不回头”;而另一个则侧重于搜索的广泛性。这么说吧一个是线性的搜索,另一个是面性的搜索。
接下来就是详细的解释了
广度优先搜索,以一个点为中心,不断向周围探索,先探索中心点的周围四个格子,再将中心按顺序转为一个个新的格子,再向自己的周围探索......就这样循环,向周围扩散式探索;比如指定A为中心点,先探索A四周的格子,依次为B、C、D、E。完成后再将中心点转为B,继续探索B的四周(探索过的除外)为1、2、3。再转为C,探索四周,转为D,探索四周,转为E,探索四周,再继续转为1,探索四周......2......3......这样循环下去,不理解的可以自己动手画个图,会对理解有帮助。
正文开始
迷宫出口
题目描述 :一天Extense在森林里探险的时候不小心走入了一个迷宫,迷宫可以 看成是由 n×n 的格点组成,每个格点只有 2 种状态, 0 和 1,前者表示可以通行后者表示不能通行。同时当Extense处在某个格点时,他只能移动到东南西北(或者说上下左右)四个方向之一的相邻格点上,Extense想要从点 A 走到点 B , 问在不走出迷宫的情况下能不能办到。 如果起点或者终点有一个不能通行(为 11),则看成无法办到。
输入 第 1 行是一个正整数 n (1≤n≤100),表示迷宫的规模是 n×n 的。 接下来是一个 n×n 的矩阵,矩阵中的元素为 0 或者 1。 再接下来一行是 4 个整数 表示入口和出口的坐标。 输出: 能办到则输出 YES,否则输出 NO。
样例
输入复制
3
0 1 1
0 0 1
1 0 0
1 1 3 3
输出复制
YES
#include<bits/stdc++.h>
using namespace std;
int a[110][110]={0};
int x[110]={0};
int y[110]={0};
int n=0;
int q=0,p=0;
int s1,s2,e1,e2;
bool jian_ce(int,int);
int main()
{cin>>n;for(int i=0;i<n;i++){for(int j=0;j<n;j++){cin>>a[i][j];}}cin>>s1>>s2>>e1>>e2;s1--;s2--;e1--;e2--;q++;x[q]=1;y[q]=1;p++;while(true){if(a[x[p]+1][y[p]]!=1&&x[p]+1<n){q++;x[q]=x[q-1]+1;y[q]=y[q-1];if(jian_ce(x[q],y[q])==true)return 0;}if(a[x[p]][y[p]+1]!=1&&y[p]+1<n){q++;x[q]=x[q];y[q]=y[q]+1;if(jian_ce(x[q],y[q])==true)return 0;}if(a[x[p]-1][y[p]]!=1&&x[p]-1>=0){q++;x[q]=x[q]-1;y[q]=y[q];if(jian_ce(x[q],y[q])==true)return 0;}if(a[x[p]][y[p]-1]!=1&&y[p]-1>=0){q++;x[q]=x[q];y[q]=y[q]-1;if(jian_ce(x[q],y[q])==true)return 0;}p++;}cout<<"NO";return 0;
}
bool jian_ce(int t1,int t2)
{if(t1==e1&&t2==e2){cout<<"YES";return true;}return false;
}至于为什么没更新,因为.........懒得q(≧▽≦q)
相关文章:

C++广度优先搜索
简介 老规矩,先来介绍一下什么是广度优先搜索(至于这么长时间没更新是为什么,我放在文章结尾了,感兴趣可以看看,以后也是如此) 广度优先搜索,从名字就能听出来,他和深度优先搜索关…...

SVN 提交与原有文件类型不一样的文件时的操作
SVN 提交与原有文件类型不一样的文件时的操作 背景 SVN 服务器上原本的文件是软链接类型的,但是我将它改成普通文件再上传。出现了以下提示: 解决过程 本来想着通过 svn rm 和 svn add 来解决,但是行不通。 最终解决方案 svn rm --keep-…...
活动预告 | Power Hour: Copilot 引领商业应用的未来
课程介绍 智能化时代,商业应用如何实现突破?微软全球副总裁 Charles Lamanna 将为您深度解析,剖析其中关键因素。 在本次线上研讨会中,Charles Lamanna 将分享他在增强商业运营方面的独到见解与实战策略,深度解读商业…...
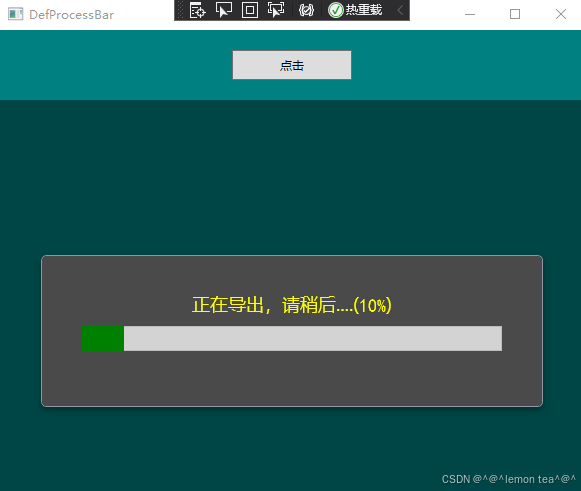
WPF 进度条(ProgressBar)示例一
本文讲述:WPF 进度条(ProgressBar)简单的样式修改和使用。 进度显示界面:使用UserControl把ProgressBar和进度值以及要显示的内容全部组装在UserControl界面中,方便其他界面直接进行使用。 <UserControl x:Class"DefProcessBarDemo…...

【C#】任务调度的实现原理与组件应用Quartz.Net
Quartz 是一个流行的开源作业调度库,最初由 Terracotta 开发,现在由 Terracotta 的一部分 Oracle 所有。它主要用于在 Java 应用程序中调度作业的执行。Quartz 使用了一种复杂的底层算法来管理任务调度,其中包括任务触发、执行、持久化以及集…...

UV - Python 包管理
文章目录 创建 uv 项目已有项目已有uv项目 创建 uv 项目 # 创建项目 uv init m3 # 创建环境 cd m3 uv venv --python 3.11 # 激活环境 source .venv/bin/activate # 添加库 uv add flask 如果创建项目后,给库取别的名字,add 的时候,会…...

pytorch torch.linalg模块介绍
torch.linalg 是 PyTorch 的 线性代数 (Linear Algebra) 子模块,它提供了许多 高效的矩阵操作和分解方法,类似于 NumPy 的 numpy.linalg 或 SciPy 的 scipy.linalg,但针对 GPU 加速和自动微分 进行了优化。 1. 矩阵基本运算 矩阵乘法 torc…...

光伏-报告显示,假期内,硅料端签单顺序发货相对稳定。若3月份下游存提产,则不排除硅料价格有上调预期。
据TrendForce集邦咨询报告显示,假期内,硅料端按照前期签单顺序发货,相对稳定。若3月份下游存提产,则不排除硅料价格有上调预期。 002306中科云网 旅游 | 公司为提供复合菜系特色餐饮的连锁企业,形成了以粤菜ÿ…...

【web自动化】指定chromedriver以及chrome路径
selenium自动化,指定chromedriver,以及chrome路径 对应这篇文章,可以点击查看,详情 from selenium import webdriverdef get_driver():# 获取配置对象option webdriver.ChromeOptions()option.add_experimental_option("de…...
面试题及参考答案)
顺丰数据分析(数据挖掘)面试题及参考答案
你觉得数据分析人员必备的技能有哪些? 数据分析人员需具备多方面技能,以应对复杂的数据处理与解读工作。 数据处理能力:这是基础且关键的技能。数据常以杂乱、不完整的形式存在,需通过清洗,去除重复、错误及缺失值数据,确保数据质量。例如,在电商销售数据中,可能存在价…...

Android studio:顶部导航栏Toolbar
主流APP在顶部都配有导航栏,在 Android 中,ActionBar 是默认启用的,它是位于屏幕顶部的一个工具栏,用来放置应用的标题、导航和操作菜单。 如果你想使用自定义的 Toolbar 来替代 ActionBar,应该先关闭它。可以通过设置…...

mmap 文件映射
🌈 个人主页:Zfox_ 🔥 系列专栏:Linux 目录 一:🔥 mmap介绍🦋 基本说明🦋 参数介绍🦋 返回值 二:🔥 demo代码🦋 写入映射🦋…...

基于微信小程序的医院预约挂号系统的设计与实现
hello hello~ ,这里是 code袁~💖💖 ,欢迎大家点赞🥳🥳关注💥💥收藏🌹🌹🌹 🦁作者简介:一名喜欢分享和记录学习的在校大学生…...

【Linux】Socket编程—UDP
🔥 个人主页:大耳朵土土垚 🔥 所属专栏:Linux系统编程 这里将会不定期更新有关Linux的内容,欢迎大家点赞,收藏,评论🥳🥳🎉🎉🎉 文章目…...

2025年物联网相关专业毕业论文选题参考,文末联系,选题相关资料提供
一、智能穿戴解决方案研究方向 序号解决方案论文选题论文研究方向1智能腰带健康监测基于SpringBoot和Vue的智能腰带健康监测数据可视化平台开发研究如何利用SpringBoot和Vue技术栈开发一个数据可视化平台,用于展示智能腰带健康监测采集的数据,如心率、血…...

如何在WPS和Word/Excel中直接使用DeepSeek功能
以下是将DeepSeek功能集成到WPS中的详细步骤,无需本地部署模型,直接通过官网连接使用:1. 下载并安装OfficeAI插件 (1)访问OfficeAI插件下载地址:OfficeAI助手 - 免费办公智能AI助手, AI写作,下载…...

DeepSeek之Api的使用(将DeepSeek的api集成到程序中)
一、DeepSeek API 的收费模式 前言:使用DeepSeek的api是收费的 免费版: 可能提供有限的免费额度(如每月一定次数的 API 调用),适合个人开发者或小规模项目。 付费版: 超出免费额度后,可能需要按…...

使用DeepSeek实现AI自动编码
最近deepseek很火,低成本训练大模型把OpenAI、英伟达等股票搞得一塌糊涂。那它是什么呢,对于咱们程序员编码能有什么用呢?DeepSeek 是一款先进的人工智能语言模型,在自然语言处理和代码生成方面表现出色。它经过大量代码数据训练&…...

30~32.ppt
目录 30.导游小姚-介绍首都北京❗ 题目 解析 31.小张-旅游产品推广文章 题目 解析 32.小李-水的知识❗ 题目 解析 30.导游小姚-介绍首都北京❗ 题目 解析 新建幻灯片-从大纲-重置-检查设计→主题对话框→浏览主题:考生文件夹(注意&#x…...

Java的匿名内部类转为lamada表达式
在Java中,匿名内部类通常用于创建没有命名类的实例。例如,你可能需要创建一个实现了某个接口的匿名类,或者在需要重写某个方法时使用它。在Java 8及更高版本中,你可以使用Lambda表达式来替代传统的匿名内部类,使得代码…...

网络编程(Modbus进阶)
思维导图 Modbus RTU(先学一点理论) 概念 Modbus RTU 是工业自动化领域 最广泛应用的串行通信协议,由 Modicon 公司(现施耐德电气)于 1979 年推出。它以 高效率、强健性、易实现的特点成为工业控制系统的通信标准。 包…...

设计模式和设计原则回顾
设计模式和设计原则回顾 23种设计模式是设计原则的完美体现,设计原则设计原则是设计模式的理论基石, 设计模式 在经典的设计模式分类中(如《设计模式:可复用面向对象软件的基础》一书中),总共有23种设计模式,分为三大类: 一、创建型模式(5种) 1. 单例模式(Sing…...
使用rpicam-app通过网络流式传输视频)
树莓派超全系列教程文档--(62)使用rpicam-app通过网络流式传输视频
使用rpicam-app通过网络流式传输视频 使用 rpicam-app 通过网络流式传输视频UDPTCPRTSPlibavGStreamerRTPlibcamerasrc GStreamer 元素 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 使用 rpicam-app 通过网络流式传输视频 本节介绍来自 rpica…...

在鸿蒙HarmonyOS 5中实现抖音风格的点赞功能
下面我将详细介绍如何使用HarmonyOS SDK在HarmonyOS 5中实现类似抖音的点赞功能,包括动画效果、数据同步和交互优化。 1. 基础点赞功能实现 1.1 创建数据模型 // VideoModel.ets export class VideoModel {id: string "";title: string ""…...
Cesium相机控制)
三维GIS开发cesium智慧地铁教程(5)Cesium相机控制
一、环境搭建 <script src"../cesium1.99/Build/Cesium/Cesium.js"></script> <link rel"stylesheet" href"../cesium1.99/Build/Cesium/Widgets/widgets.css"> 关键配置点: 路径验证:确保相对路径.…...

PPT|230页| 制造集团企业供应链端到端的数字化解决方案:从需求到结算的全链路业务闭环构建
制造业采购供应链管理是企业运营的核心环节,供应链协同管理在供应链上下游企业之间建立紧密的合作关系,通过信息共享、资源整合、业务协同等方式,实现供应链的全面管理和优化,提高供应链的效率和透明度,降低供应链的成…...

JVM垃圾回收机制全解析
Java虚拟机(JVM)中的垃圾收集器(Garbage Collector,简称GC)是用于自动管理内存的机制。它负责识别和清除不再被程序使用的对象,从而释放内存空间,避免内存泄漏和内存溢出等问题。垃圾收集器在Ja…...

2025季度云服务器排行榜
在全球云服务器市场,各厂商的排名和地位并非一成不变,而是由其独特的优势、战略布局和市场适应性共同决定的。以下是根据2025年市场趋势,对主要云服务器厂商在排行榜中占据重要位置的原因和优势进行深度分析: 一、全球“三巨头”…...

学习一下用鸿蒙DevEco Studio HarmonyOS5实现百度地图
在鸿蒙(HarmonyOS5)中集成百度地图,可以通过以下步骤和技术方案实现。结合鸿蒙的分布式能力和百度地图的API,可以构建跨设备的定位、导航和地图展示功能。 1. 鸿蒙环境准备 开发工具:下载安装 De…...

图解JavaScript原型:原型链及其分析 | JavaScript图解
忽略该图的细节(如内存地址值没有用二进制) 以下是对该图进一步的理解和总结 1. JS 对象概念的辨析 对象是什么:保存在堆中一块区域,同时在栈中有一块区域保存其在堆中的地址(也就是我们通常说的该变量指向谁&…...
