每日一题——括号生成
题解
给定 n 对括号,要求编写一个函数生成所有合法的括号组合。合法的括号组合必须满足每一对括号中的左括号必须先于右括号,并且括号数量必须平衡。
题目描述
输入:
- 一个整数
n,表示括号的对数,满足 0 ≤ n ≤ 10 0 \leq n \leq 10 0≤n≤10。
输出:
- 返回一个包含所有合法括号组合的字符串数组。
示例1
输入:
1
输出:
["()"]
示例2
输入:
2
输出:
["(())", "()()"]
题解思路
这个问题是一个典型的递归回溯问题。我们可以通过递归来生成所有可能的括号组合。具体步骤如下:
- 用递归函数生成括号的组合。
- 每次递归调用时,有两个选择:
- 如果左括号还没有用完,就添加一个左括号
'('。 - 如果右括号的数量小于左括号的数量,且右括号还没有用完,就添加一个右括号
')'。
- 如果左括号还没有用完,就添加一个左括号
- 当左右括号的数量都达到了
n时,表示一个合法的组合已经完成,将其加入结果数组。
时间复杂度和空间复杂度
- 时间复杂度:O( 2 n 2^n 2n),因为每一层递归有两种选择(添加左括号或右括号)。
- 空间复杂度:O( n n n),由于递归调用栈的深度是
n,每次递归都在2n长度的字符串上操作。
代码实现
#include <stdio.h>
#include <stdlib.h>
#include <string.h>/*** 深度优先搜索(DFS)函数,用于生成所有有效的括号组合* * @param left 左括号的数量* @param right 右括号的数量* @param ret 存储所有生成的括号组合的数组* @param path 当前路径,即当前生成的括号组合* @param n 括号对数* @param returnSize 当前已生成的括号组合数量*/
void DFS(int left, int right, char **ret, char* path, int n, int *returnSize) {// 如果左括号和右括号的数量都等于 n,说明生成了一个有效的括号组合if (left == n && right == n) {// 为当前括号组合分配内存,长度为 2n + 1(包括字符串终止符)ret[*returnSize] = malloc(sizeof(char) * (2 * n + 1));if (ret[*returnSize] == NULL) {printf("Memory allocation failed\n");exit(1);}// 将当前路径复制到结果数组中for (int i = 0; i < 2 * n; i++) {ret[*returnSize][i] = path[i];}ret[*returnSize][2 * n] = '\0'; // 添加字符串终止符// 增加已生成的括号组合数量(*returnSize)++;return;}// 如果左括号的数量小于 n,可以添加一个左括号if (left < n) {path[left + right] = '('; // 在当前路径中添加左括号DFS(left + 1, right, ret, path, n, returnSize); // 递归调用,继续生成}// 如果右括号的数量小于左括号的数量且小于 n,可以添加一个右括号if (right < left && right < n) {path[left + right] = ')'; // 在当前路径中添加右括号DFS(left, right + 1, ret, path, n, returnSize); // 递归调用,继续生成}
}/*** 主函数,生成所有有效的括号组合* * @param n 括号对数* @param returnSize 返回的括号组合数量* @return 存储所有有效括号组合的数组*/
char** generateParenthesis(int n, int *returnSize) {// 预分配足够大的空间存储结果,这里假设最多有 2000 种组合char** ret = (char**)malloc(sizeof(char*) * 2000);if (ret == NULL) {printf("Memory allocation failed\n");exit(1);}*returnSize = 0; // 初始化返回的括号组合数量为 0// 为当前路径分配内存,长度为 2n + 1(包括字符串终止符)char* path = (char*)malloc(sizeof(char) * (2 * n + 1));if (path == NULL) {printf("Memory allocation failed\n");exit(1);}// 调用 DFS 函数生成所有有效的括号组合DFS(0, 0, ret, path, n, returnSize);// 释放当前路径的内存free(path);return ret;
}解析
-
DFS函数的递归逻辑:
DFS(left, right, ret, str, n, returnSize)是递归的核心函数,left和right分别表示已使用的左括号和右括号数量。- 如果
left和right都达到了n,就将当前字符串str(存放括号组合)存入ret数组。 - 如果
left < n,我们可以继续添加左括号。 - 如果
right < left,我们可以继续添加右括号。
-
空间分配:
- 结果数组
ret被分配了2000个空间,可以容纳所有合法组合(理论上可能达到O(4^n)个组合,但实际上不会达到这么多)。 - 每个合法的括号组合是一个长度为2n的字符串,因此
str的长度是2n。
- 结果数组
-
返回值:
ret返回存放合法括号组合的数组,returnSize返回合法组合的数量。
总结
通过递归的方式,我们能够高效地生成所有合法的括号组合。递归回溯方法简洁而直观,适合解决此类组合生成的问题。
相关文章:

每日一题——括号生成
题解 给定 n 对括号,要求编写一个函数生成所有合法的括号组合。合法的括号组合必须满足每一对括号中的左括号必须先于右括号,并且括号数量必须平衡。 题目描述 输入: 一个整数 n,表示括号的对数,满足 0 ≤ n ≤ 1…...

实操部署DeepSeek,添加私有知识库
目录 一、环境介绍 PowerShell版本: wsl版本: 虚拟机版本: 本机IP: 虚拟机IP: 容器宿主机IP(host.docker.internal): Docker版本: Docker Compose版本ÿ…...

宜宾数字经济新标杆:树莓集团赋能区域产业转型升级
树莓集团在宜宾成为数字经济新标杆,有力地赋能区域产业转型升级。在传统产业数字化转型方面,树莓集团针对宜宾的制造业企业,引入工业互联网技术。 通过搭建工业互联网平台,实现企业生产设备的联网和数据采集,帮助企业…...

8.大规模推荐系统的实现
接下来我们将学习大规模推荐系统的实现。在实际应用中,推荐系统需要处理海量数据,并在短时间内生成推荐结果。这要求我们在设计和实现推荐系统时,考虑到数据的分布式存储与处理、计算的高效性和系统的可扩展性。在这一课中,我们将…...
第三届通信网络与机器学习国际学术会议(CNML 2025)
在线投稿: 学术会议-学术交流征稿-学术会议在线-艾思科蓝 通信网络机器学习 通信理论 通信工程 计算机网络和数据通信 信息分析和基础设施 通信建模理论与实践 无线传感器和通信网络 云计算与物联网 网络和数据安全 光电子学和光通信 无线/移动通信和技术 智能通信…...

MySQL两阶段提交策略
书接上一篇文章,MySQL通过不同的策略来保证事务的ACID:原子性、一致性、隔离性、持久性,通过锁机制实现隔离性,通过redoundobinlog三种日志实现事务的原子性、一致性和持久性。 本文主要讲MySQL的持久性的一个实现机制-两阶段提交…...
uniapp商城之购物车模块
文章目录 一、列表渲染二、删除单品1.封装删除API2.按钮绑定事件三、修改单品数量1.复用步进器组件2.属性和事件的绑定3.接口封装4.调用接口四、修改商品选中/全选1.单品选中绑定事件调用修改API2.计算全选状态3.绑定事件调用全选API并渲染单品选中状态五、底部结算信息1.计算选…...

STM32_USART通用同步/异步收发器
目录 背景 程序 STM32浮空输入的概念 1.基本概念 2. STM32浮空输入的特点 3. STM32浮空输入的应用场景 STM32推挽输出详解 1. 基本概念 2. 工作原理 3. 应用场景 使能外设时钟 TXE 和 TC的区别 USART_IT_TXE USART_IT_TC 使能串口外设 中断处理函数 背景 单片…...
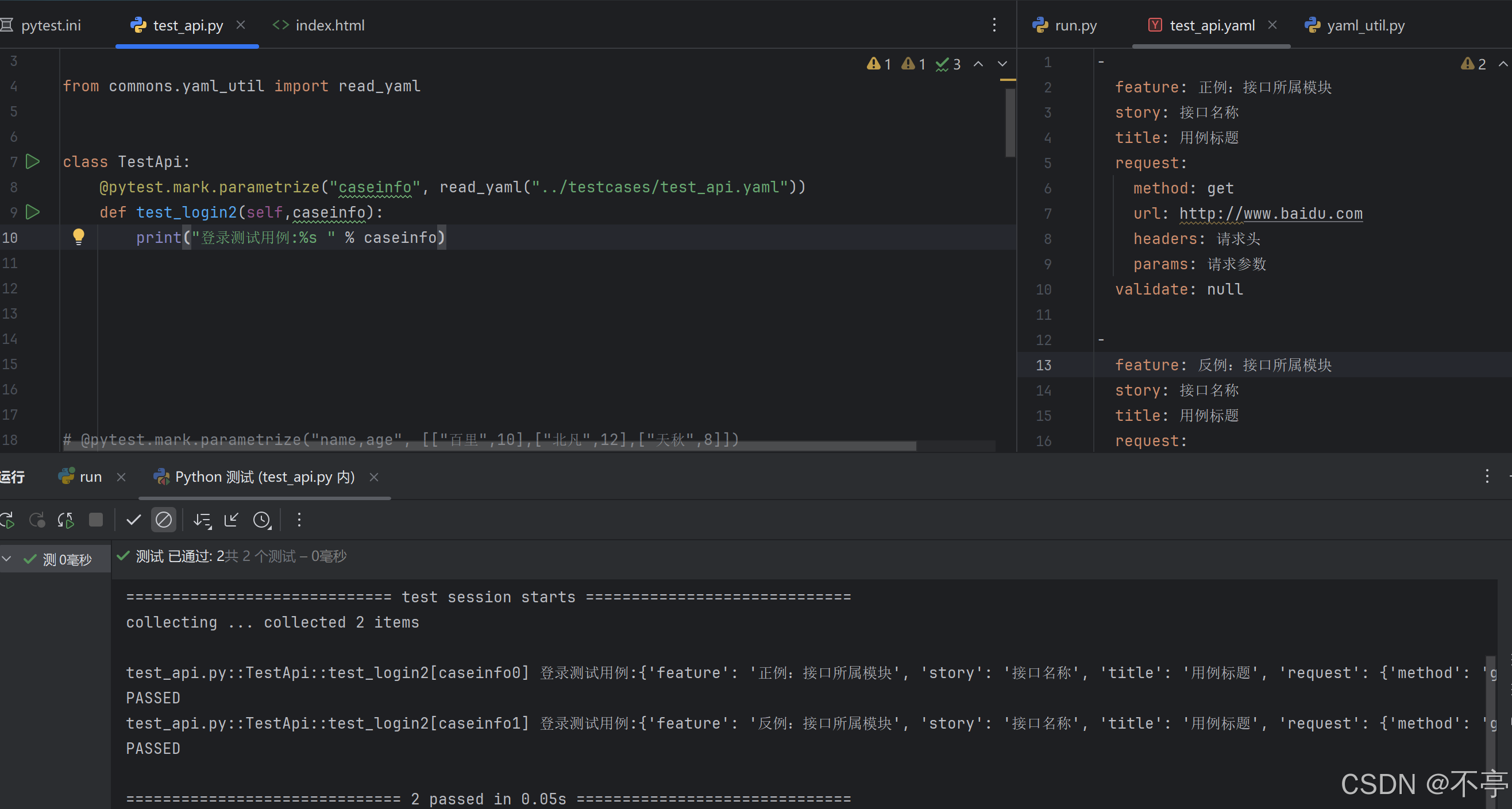
python自动化测试之Pytest框架之YAML详解以及Parametrize数据驱动!
一、YAML详解 YAML是一种数据类型,它能够和JSON数据相互转化,它本身也是有很多数据类型可以满足我们接口 的参数类型,扩展名可以是.yml或.yaml 作用: 1.全局配置文件 基础路径,数据库信息,账号信息&…...

python基础入门:6.3异常处理机制
Python异常处理全面指南:构建健壮程序的关键技术 # 完整异常处理模板 def process_file(file_path):"""文件处理示例函数"""file Nonetry:file open(file_path, r, encodingutf-8)data json.load(file)if not data:raise EmptyDa…...
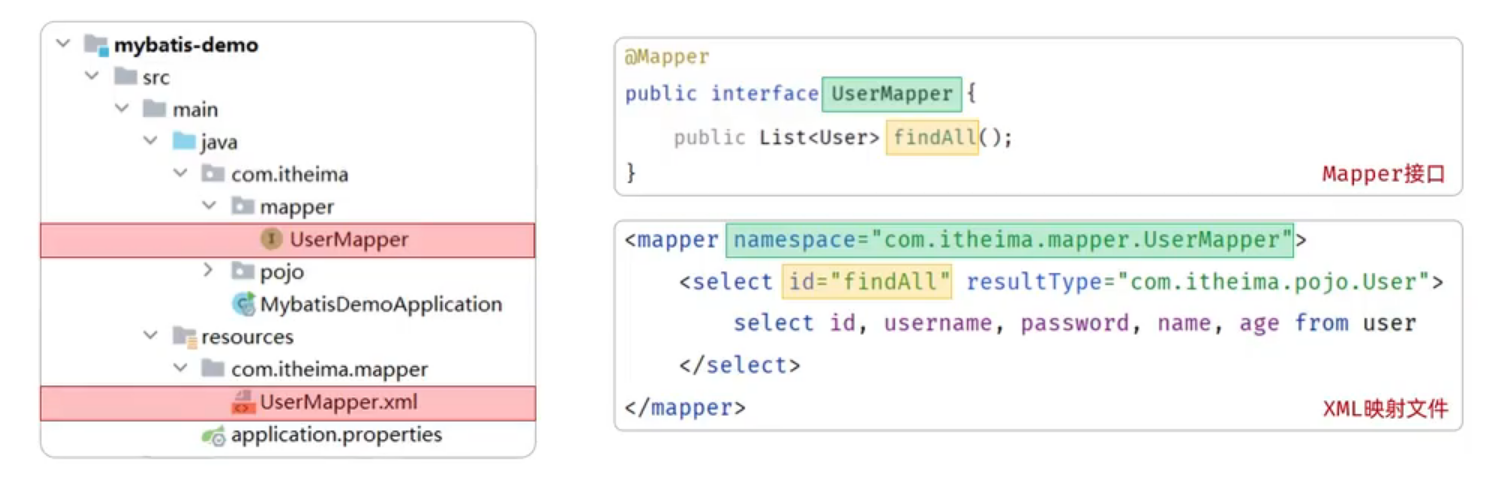
Mybatis快速入门与核心知识总结
Mybatis 1. 实体类(Entity Class)1.1 实体类的定义1.2 简化编写1.2.1 Data1.2.2 AllArgsConstructor1.2.3 NoArgsConstructor 2. 创建 Mapper 接口2.1 Param2.2 #{} 占位符2.3 SQL 预编译 3. 配置 MyBatis XML 映射文件(可选)3.1 …...
畅聊deepseek-r1,SiliconFlow 硅基流动注册+使用
文章目录 SiliconFlow 硅基流动注册使用注册创建API密钥使用网页端使用代码调用api调用支持的模型 SiliconFlow 硅基流动注册使用 注册 硅基流动官网 https://cloud.siliconflow.cn/i/XcgtUixn 注册流程 切换中文 邀请码: XcgtUixn 创建API密钥 账户管理 --&g…...
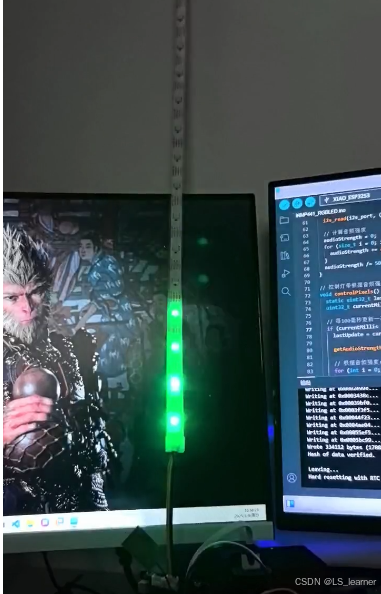
一个基于ESP32S3和INMP441麦克风实现音频强度控制RGB灯带律动的代码及效果展示
一个基于ESP32S3和INMP441麦克风实现音频强度控制RGB灯带律动的代码示例,使用Arduino语言: 硬件连接 INMP441 VCC → ESP32的3.3VINMP441 GND → ESP32的GNDINMP441 SCK → ESP32的GPIO 17INMP441 WS → ESP32的GPIO 18INMP441 SD → ESP32的GPIO 16RG…...
Springboot 中如何使用Sentinel
在 Spring Boot 中使用 Sentinel 非常方便,Spring Cloud Alibaba 提供了 spring-cloud-starter-alibaba-sentinel 组件,可以快速将 Sentinel 集成到你的 Spring Boot 应用中,并利用其强大的流量控制和容错能力。 下面是一个详细的步骤指南 …...
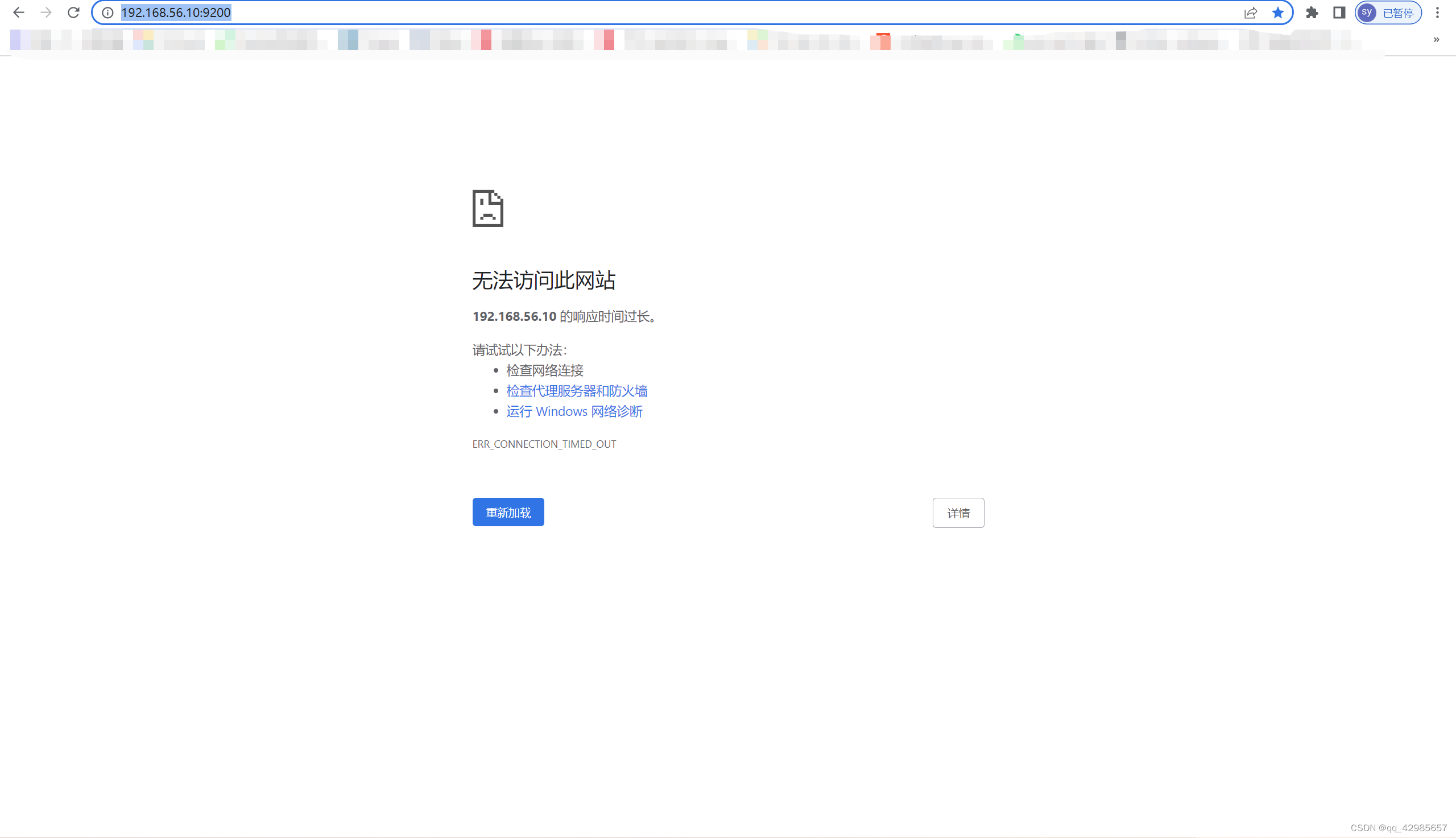
访问Elasticsearch服务 curl ip 端口可以 浏览器不可以
LINUX学习 在虚拟机上面的linux上面用docker 部署Elasticsearch项目后,在linux系统内部用curl ip 端口地址的形式可以访问到Elasticsearch。可以返回数据。 但是在本机的浏览器中输入ip 端口,会报错,找不到服务。 ping 和 trelnet均不通。 …...
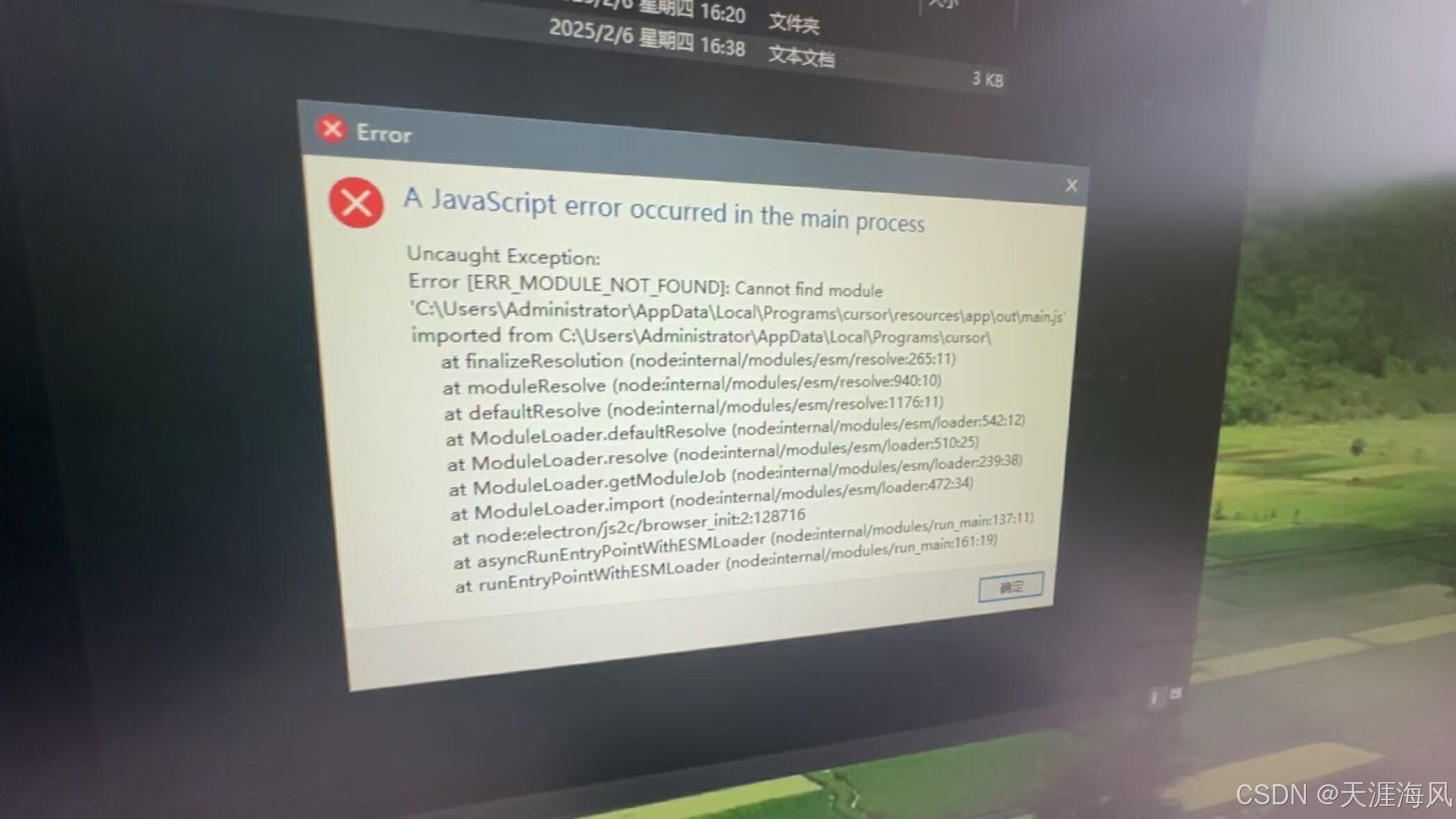
Curser2_解除机器码限制
# Curser1_无限白嫖试用次数 文末有所需工具下载地址 Cursor Device ID Changer 一个用于修改 Cursor 编辑器设备 ID 的跨平台工具集。当遇到设备 ID 锁定问题时,可用于重置设备标识。 功能特性 ✨ 支持 Windows 和 macOS 系统🔄 自动生成符合格式的…...
人工智能与低代码如何重新定义企业数字化转型?
引言:数字化转型的挑战与机遇 在全球化和信息化的浪潮中,数字化转型已经成为企业保持竞争力和创新能力的必经之路。然而,尽管“数字化”听上去是一个充满未来感的词汇,落地的过程却往往充满困难。 首先,传统开发方式…...
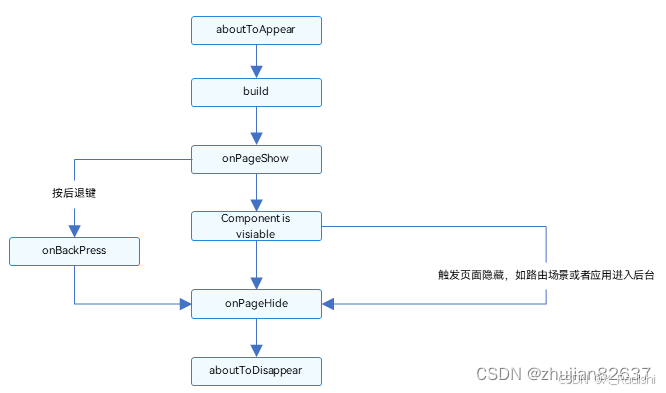
arkTS基础
arkTS基础 // 变量声明 let hi: string hello; hi hello,world; // 常量声明 const hi: string hello;// ArkTS是一种静态类型语言,所有数据的类型都必须在编译时确定 // 如果一个变量或常量的声明包含了初始值,那么开发者就不需要显式指定其类型。…...

C++20中的std::atomic_ref
一、std::atomic_ref 我们在学习C11后的原子操作时,都需要提前定义好std::atomic变量,然后才可以在后续的应用程序中进行使用。原子操作的优势在很多场合下优势非常明显,所以这也使得很多开发者越来习惯使用原子变量。 但是,在实…...

四、自然语言处理_08Transformer翻译任务案例
0、前言 在Seq2Seq模型的学习过程中,做过一个文本翻译任务案例,多轮训练后,效果还算能看 Transformer作为NLP领域的扛把子,对于此类任务的处理会更为强大,下面将以基于Transformer模型来重新处理此任务,看…...

黑马Mybatis
Mybatis 表现层:页面展示 业务层:逻辑处理 持久层:持久数据化保存 在这里插入图片描述 Mybatis快速入门 
day52 ResNet18 CBAM
在深度学习的旅程中,我们不断探索如何提升模型的性能。今天,我将分享我在 ResNet18 模型中插入 CBAM(Convolutional Block Attention Module)模块,并采用分阶段微调策略的实践过程。通过这个过程,我不仅提升…...

多种风格导航菜单 HTML 实现(附源码)
下面我将为您展示 6 种不同风格的导航菜单实现,每种都包含完整 HTML、CSS 和 JavaScript 代码。 1. 简约水平导航栏 <!DOCTYPE html> <html lang"zh-CN"> <head><meta charset"UTF-8"><meta name"viewport&qu…...

ArcGIS Pro制作水平横向图例+多级标注
今天介绍下载ArcGIS Pro中如何设置水平横向图例。 之前我们介绍了ArcGIS的横向图例制作:ArcGIS横向、多列图例、顺序重排、符号居中、批量更改图例符号等等(ArcGIS出图图例8大技巧),那这次我们看看ArcGIS Pro如何更加快捷的操作。…...

Swagger和OpenApi的前世今生
Swagger与OpenAPI的关系演进是API标准化进程中的重要篇章,二者共同塑造了现代RESTful API的开发范式。 本期就扒一扒其技术演进的关键节点与核心逻辑: 🔄 一、起源与初创期:Swagger的诞生(2010-2014) 核心…...

C++:多态机制详解
目录 一. 多态的概念 1.静态多态(编译时多态) 二.动态多态的定义及实现 1.多态的构成条件 2.虚函数 3.虚函数的重写/覆盖 4.虚函数重写的一些其他问题 1).协变 2).析构函数的重写 5.override 和 final关键字 1&#…...

Vue 3 + WebSocket 实战:公司通知实时推送功能详解
📢 Vue 3 WebSocket 实战:公司通知实时推送功能详解 📌 收藏 点赞 关注,项目中要用到推送功能时就不怕找不到了! 实时通知是企业系统中常见的功能,比如:管理员发布通知后,所有用户…...

数据库——redis
一、Redis 介绍 1. 概述 Redis(Remote Dictionary Server)是一个开源的、高性能的内存键值数据库系统,具有以下核心特点: 内存存储架构:数据主要存储在内存中,提供微秒级的读写响应 多数据结构支持&…...

负载均衡器》》LVS、Nginx、HAproxy 区别
虚拟主机 先4,后7...

Canal环境搭建并实现和ES数据同步
作者:田超凡 日期:2025年6月7日 Canal安装,启动端口11111、8082: 安装canal-deployer服务端: https://github.com/alibaba/canal/releases/1.1.7/canal.deployer-1.1.7.tar.gz cd /opt/homebrew/etc mkdir canal…...
