[c语言日寄]在不完全递增序中查找特定要素

【作者主页】siy2333
【专栏介绍】⌈c语言日寄⌋:这是一个专注于C语言刷题的专栏,精选题目,搭配详细题解、拓展算法。从基础语法到复杂算法,题目涉及的知识点全面覆盖,助力你系统提升。无论你是初学者,还是进阶开发者,这里都能满足你的需求!
【食用方法】1.根据题目自行尝试 2.查看基础思路完善题解 3.学习拓展算法
【Gitee链接】资源保存在我的Gitee仓库:https://gitee.com/siy2333/study
文章目录
- 前言
- 一、题目引入
- 不完全递增矩阵
- 问题描述
- 二、知识点分析
- 三、解法实现与分析
- 1. 暴力搜索
- 2. 逐行二分查找
- 四、总结
前言
查找类问题是一个非常常见的任务。无论是从简单的数组中查找一个特定的数字,还是从复杂的数据结构中检索信息,查找算法的效率和正确性都十分重要。今天,我们将探讨一个有趣的查找问题:在不完全递增序的矩阵中查找特定的元素。
一、题目引入
不完全递增矩阵
假设我们有一个二维矩阵,矩阵的每一行从左到右是递增的,但列与列之间并没有严格的递增关系。这种矩阵被称为“不完全递增序矩阵”。
例如,以下矩阵满足这一条件
1 3 5 7 2 4 6 8 10 11 12 13 9 14 15 16
在这个矩阵中,每一行都是递增的,但列与列之间并不完全递增。
问题描述
给定一个不完全递增序的矩阵和一个目标数字,编写一个程序来判断该数字是否存在于矩阵中。
假设矩阵如下,而且目标数字为 12:
| 1 | 3 | 5 | 7 |
|---|---|---|---|
| 2 | 4 | 6 | 8 |
| 10 | 11 | 12 | 13 |
| 9 | 14 | 15 | 16 |
此时,程序返回 true。
二、知识点分析
- 矩阵的特性
矩阵的每一行从左到右是递增的,这意味着我们可以利用这一特性来优化查找算法。虽然列与列之间没有严格的递增关系,但行的递增性仍然可以为我们提供一些线索。我们在接下来的文章中会利用这一点解题。 - 查找算法
在完全有序的矩阵中,我们可以从右上角或左下角开始查找,利用矩阵的有序性逐步缩小搜索范围(例如二分查找)。然而,在不完全递增序的矩阵中,这种方法不再适用。我们需要寻找一种新的策略来优化查找过程。 - 时间复杂度
对于一个 M×N 的矩阵,暴力搜索的时间复杂度为 O(M×N)。
三、解法实现与分析
1. 暴力搜索
最简单的查找方法是暴力搜索,即遍历矩阵的每一个元素,检查是否等于目标值。这种方法的时间复杂度为 O(M×N),效率较低。
#include <stdio.h>
#include <stdbool.h>#define M 4
#define N 4//暴力查找函数
bool find_brute_force(int matrix[M][N], int target) {for (int i = 0; i < M; i++) {for (int j = 0; j < N; j++) {if (matrix[i][j] == target) {return true;}}}return false;
}
//主函数
int main() {//定义数组int matrix[M][N] = {{1, 3, 5, 7},{2, 4, 6, 8},{10, 11, 12, 13},{9, 14, 15, 16}};int target = 12;//查找与输出if (find_brute_force(matrix, target)) {printf("Target %d found in the matrix.\n", target);} else {printf("Target %d not found in the matrix.\n", target);}return 0;
}
运行结果如下:

2. 逐行二分查找
虽然矩阵的列没有严格的递增关系,但每一行的递增性可以被利用。我们可以对每一行进行二分查找。这种方法的时间复杂度为 O(MlogN)。
#include <stdio.h>
#include <stdbool.h>#define M 4
#define N 4bool binary_search(int arr[], int target) {int left = 0, right = N - 1;while (left <= right) {int mid = left + (right - left) / 2;if (arr[mid] == target) {return true;} else if (arr[mid] < target) {left = mid + 1;} else {right = mid - 1;}}return false;
}bool find_row_wise(int matrix[M][N], int target) {for (int i = 0; i < M; i++) {if (binary_search(matrix[i], target)) {return true;}}return false;
}int main() {int matrix[M][N] = {{1, 3, 5, 7},{2, 4, 6, 8},{10, 11, 12, 13},{9, 14, 15, 16}};int target = 12;if (find_row_wise(matrix, target)) {printf("Target %d found in the matrix.\n", target);} else {printf("Target %d not found in the matrix.\n", target);}return 0;
}
运行结果如下:

四、总结
通过分析条件的特性,选择合适的查找算法和数据结构,是程序员的重要素质。对于这道题,即不完全递增序的矩阵,逐行二分查找是一种有效的优化策略。
关注窝,每三天至少更新一篇优质c语言题目详解~
[专栏链接QwQ] :⌈c语言日寄⌋CSDN
[关注博主ava]:siy2333
感谢观看~ 我们下次再见!!
相关文章:

[c语言日寄]在不完全递增序中查找特定要素
【作者主页】siy2333 【专栏介绍】⌈c语言日寄⌋:这是一个专注于C语言刷题的专栏,精选题目,搭配详细题解、拓展算法。从基础语法到复杂算法,题目涉及的知识点全面覆盖,助力你系统提升。无论你是初学者,还是…...

Golang的多团队协作编程模式与实践经验
Golang的多团队协作编程模式与实践经验 一、多团队协作编程模式概述 在软件开发领域,多团队协作编程是一种常见的工作模式。特别是对于大型项目来说,不同团队间需要协同合作,共同完成复杂的任务。Golang作为一种高效、并发性强的编程语言&…...

cv2.Sobel
1. Sobel 算子简介 Sobel 算子是一种 边缘检测算子,通过对图像做梯度计算,可以突出边缘。 Sobel X 方向卷积核: 用于计算 水平方向(x 方向) 的梯度。 2. 输入图像示例 假设我们有一个 55 的灰度图像,像素…...

Windows软件自动化利器:pywinauto python
Pywinauto WindowsAPP UI自动化 Windows软件自动化利器:pywinauto python...

关于 IoT DC3 中驱动(Driver)的理解
在开源IoT DC3物联网系统中,驱动(Driver)扮演着至关重要的角色,它充当了软件系统与物理设备之间的桥梁。驱动的主要功能是依据特定的通信协议连接到设备,并根据设备模板中配置的位号信息进行数据采集和指令控制。不同的…...

LogicFlow自定义节点:矩形、HTML(vue3)
效果: LogicFlow 内部是基于MVVM模式进行开发的,分别使用preact和mobx来处理 view 和 model,所以当我们自定义节点的时候,需要为这个节点定义view和model。 参考官方文档:节点 | LogicFlow 1、自定义矩形节点 custo…...

多模态本地部署ConVideoX-5B模型文生视频
文章目录 一、多模态概念1.多模态学习2. 人机交互3. 健康医疗4. 内容创作和娱乐 二、模型介绍三、环境安装1. 安装工具包2. 模型下载 四、运行代码五、代码解析六、效果生成七. 总结1. 模型介绍2. 部署环境3. 部署步骤4. 生成视频5. 应用场景 一、多模态概念 多模态࿰…...

html 点击弹出视频弹窗
一、效果: 点击视频按钮后,弹出弹窗 播放视频 二、代码 <div class="index_change_video" data-video-src="</...

业务干挂数据库,Oracle内存分配不足
📢📢📢📣📣📣 作者:IT邦德 中国DBA联盟(ACDU)成员,10余年DBA工作经验 Oracle、PostgreSQL ACE CSDN博客专家及B站知名UP主,全网粉丝10万 擅长主流Oracle、MySQL、PG、高斯…...

MongoDB 7 分片副本集升级方案详解(下)
#作者:任少近 文章目录 1.4 分片升级1.5 升级shard11.6 升级shard2,shard31.7 升级mongos1.8重新启用负载均衡器1.9 推荐MongoDB Compass来验证数据 2 注意事项: 1.4 分片升级 使用“滚动”升级从 MongoDB 7.0 升级到 8.0,即在其他成员可用…...

Webpack相关优化总结
在使用webpack时提供了各种配置,这里结合在业务中常用的配置汇总一下可以进行的一系列的webpack优化 缩小文件搜索范围 其原理是在构建时,会以用户配置的Entry为开始依次递归遍历每个Module,在遍历每个Module时会调用相应合适的Loader对原模…...

ollama实践笔记
目录 一、linux安装文件命令: 二、启动ollama 三、linux 如何把ollama serve做为服务方式启动 四、安装deepseek-r1 五、如何在网页中使用ollama? 5.1 安装Open WebUI【不推荐】 5.2 安装ollama-webui-lite 六、Ubuntu安装docker、只需要一句话…...

springCloud-2021.0.9 之 服务调服务 示例
文章目录 前言springCloud-2021.0.9 之 服务调服务 示例1. 主要用到的组件2. 效果3. 源码3.1. 服务A3.2. 服务B接受接口 前言 如果您觉得有用的话,记得给博主点个赞,评论,收藏一键三连啊,写作不易啊^ _ ^。 而且听说点赞的人每…...
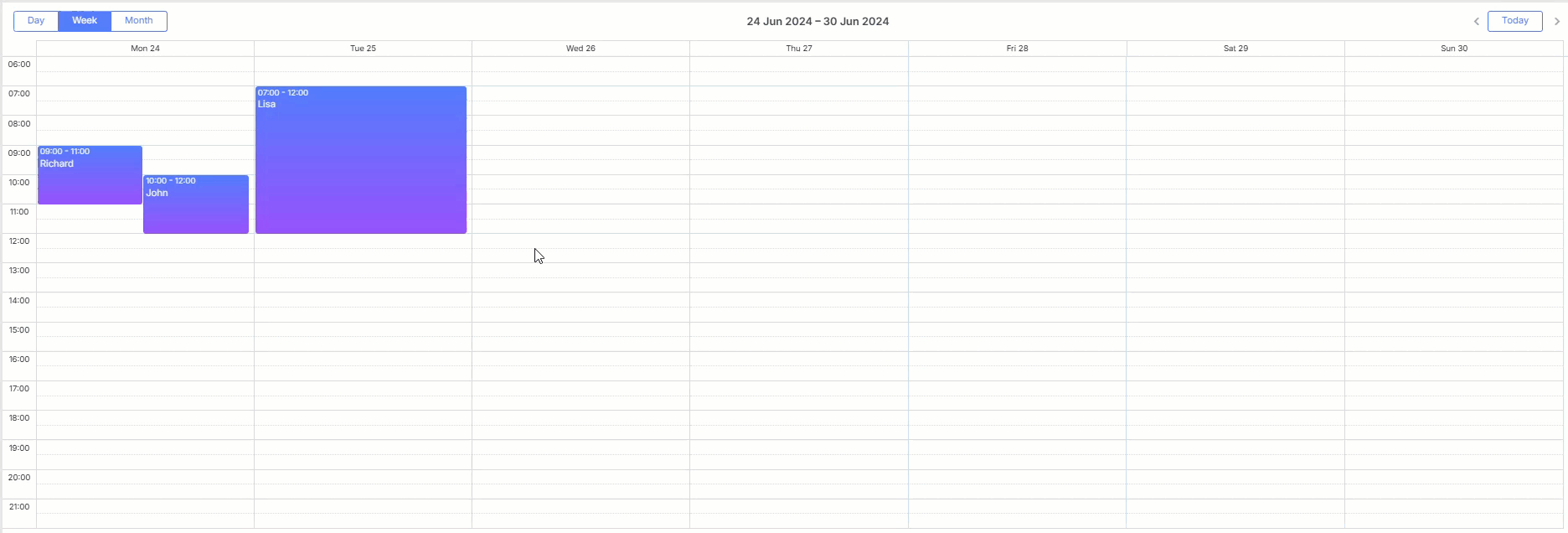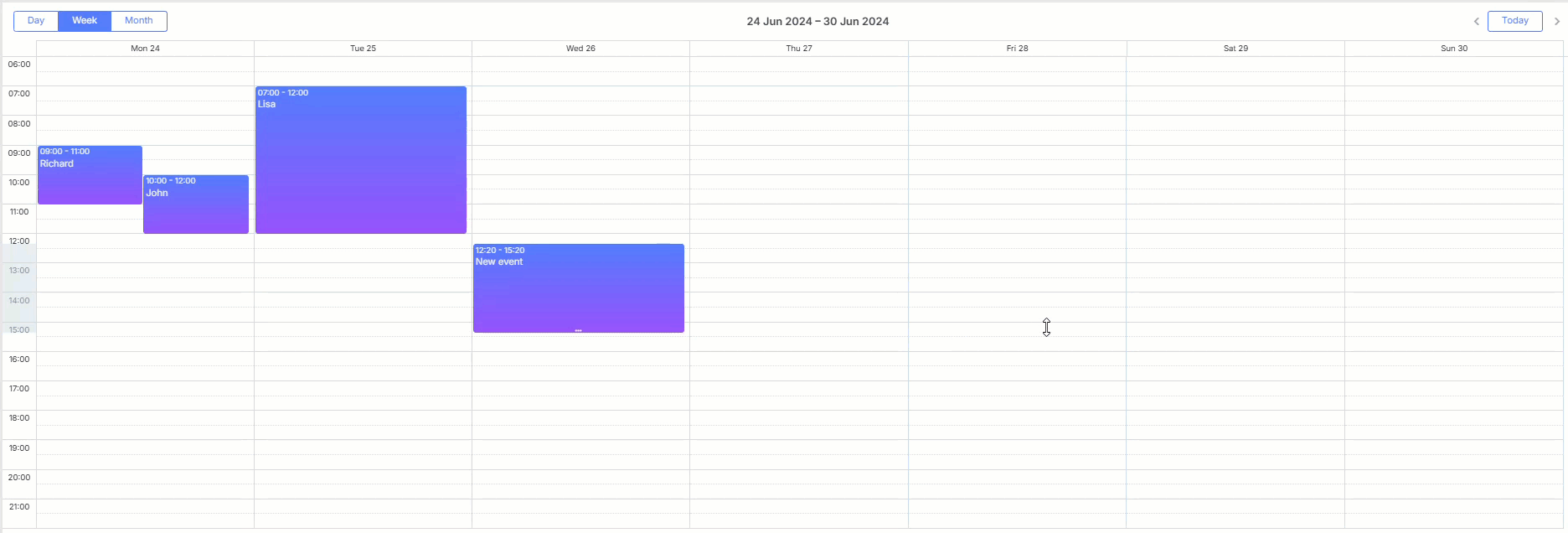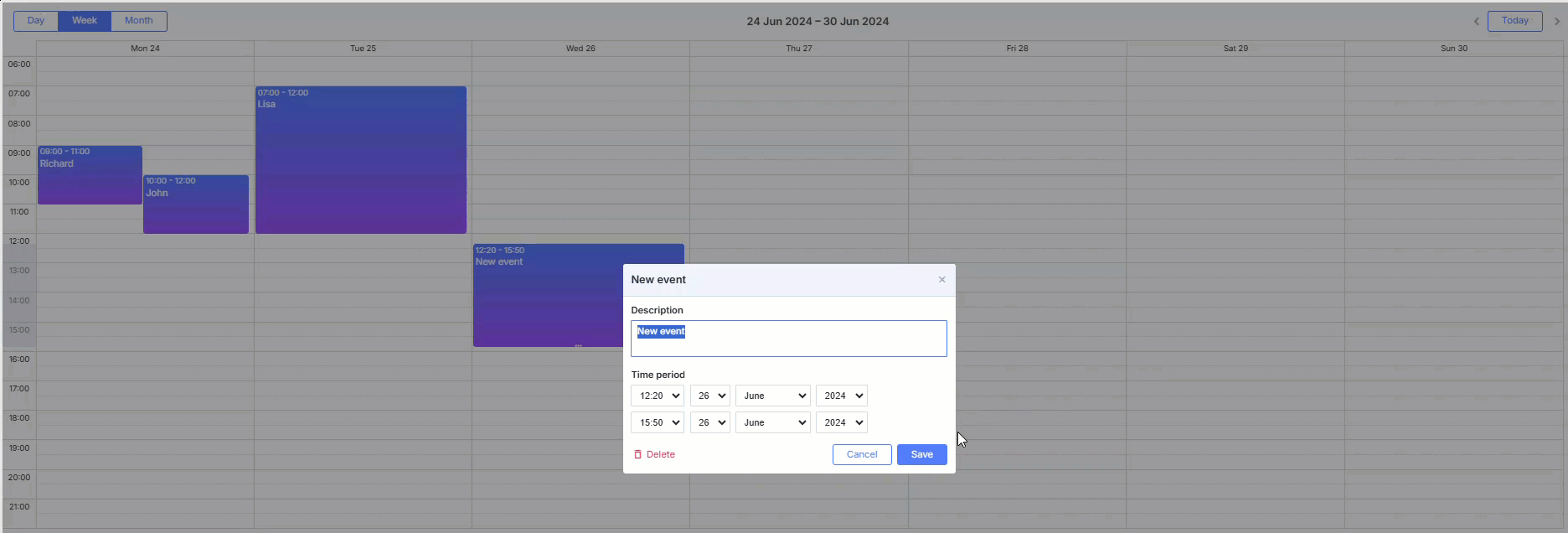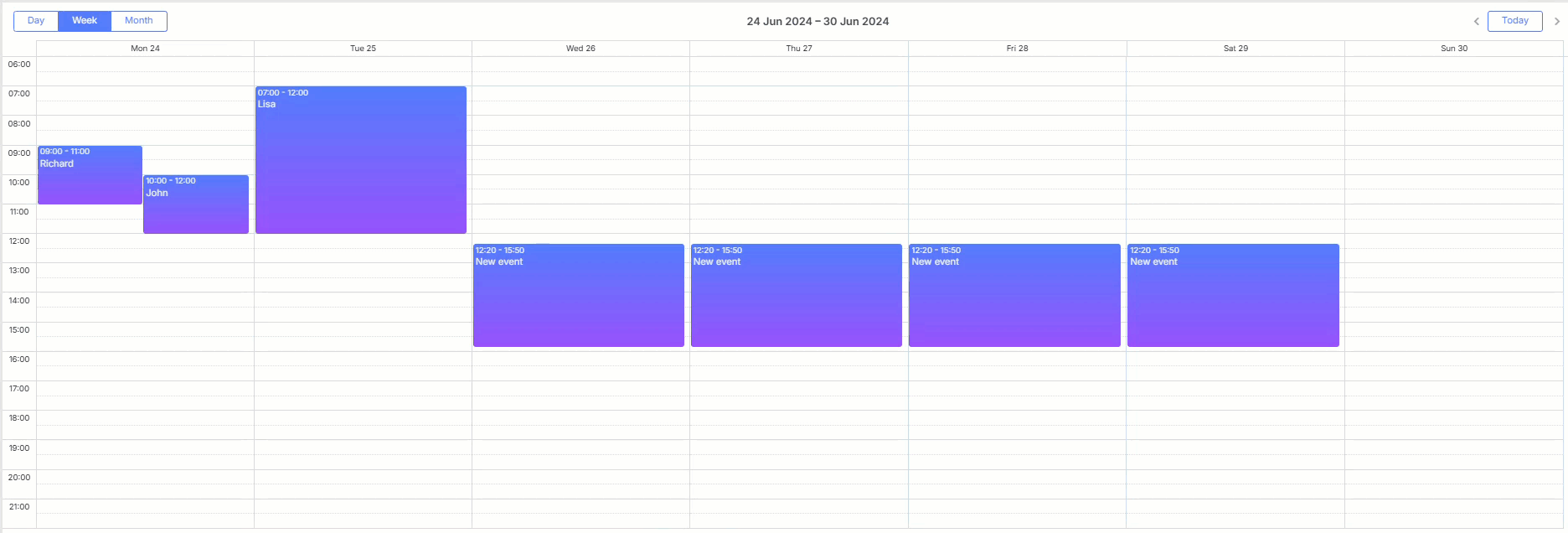
如何使用DHTMLX Scheduler的拖放功能,在 JS 日程安排日历中创建一组相同的事件
DHTMLX Scheduler 是一个全面的调度解决方案,涵盖了与规划事件相关的广泛需求。假设您在我们的 Scheduler 文档中找不到任何功能,并且希望在我们的 Scheduler 文档中看到您的项目。在这种情况下,很可能可以使用自定义解决方案来实现此类功能。…...

QxOrm生成json
下载Qxorm-1.5版本 使用vs打开项目,直接生成即可: lib目录中会生成dll和lib文件 新建Qt项目使用Qxorm: 将QxOrm中上面三个目录拷贝到新建的Qt项目中 pro文件添加使用QxOrm第三方库 INCLUDEPATH $$PWD/include/ LIBS -L"$$PWD/lib" LIBS…...
 模拟高清 寄存器手册 XS9922B 四通道 多合一模拟高清解码芯片)
XS9922B(CHIPUP) 模拟高清 寄存器手册 XS9922B 四通道 多合一模拟高清解码芯片
XS9922B 是一款 4 通道模拟复合视频解码芯片,支持 HDCCTV 高清协议和 CVBS 标 清协议,视频制式支持 720P/1080P 高清制式和 960H/D1 标清制式。芯片将接收到的高清 模拟复合视频信号经过模数转化,视频解码以及 2D 图像处理之后…...

Django创建超管用户
在 Django 中创建超级用户(superuser)可以通过命令行工具 createsuperuser 完成。以下是具体步骤: 1. 确保已进行数据库迁移 在创建超级用户前,确保已执行数据库迁移: python manage.py migrate 2. 创建超级用户 …...

基于Kotlin中Flow扩展重试方法
最近项目中统一采用Kotlin的Flow来重构了网络请求相关代码。 目前的场景是,接口在请求的时候需要一个accessToken值,因为此值会过期或者不存在,需要刷新,因此最终方案是在使用Flow请求的时候先获取accessToken值然后再进行接口请求…...

好好说话:深度学习扫盲
大创项目是和目标检测算法YOLO相关的,浅浅了解了一些有关深度学习的知识。在这里根据本人的理解做一些梳理。 深度学习是什么? 之前经常听到AI,机器学习,深度学习这三个概念,但是对于三者的区别一直很模糊。 AI&…...

【状态空间方程】对于状态空间方程矩阵D≠0时的状态反馈与滑模控制
又到新的一年啦,2025新年快乐~。前几个月都没更新,主要还是因为不能把项目上的私密工作写进去,所以暂时没啥可写的。最近在山里实习,突然想起年前遗留了个问题一直没解决,没想到这两天在deepseek的加持下很快解决了&am…...

铭豹扩展坞 USB转网口 突然无法识别解决方法
当 USB 转网口扩展坞在一台笔记本上无法识别,但在其他电脑上正常工作时,问题通常出在笔记本自身或其与扩展坞的兼容性上。以下是系统化的定位思路和排查步骤,帮助你快速找到故障原因: 背景: 一个M-pard(铭豹)扩展坞的网卡突然无法识别了,扩展出来的三个USB接口正常。…...

XCTF-web-easyupload
试了试php,php7,pht,phtml等,都没有用 尝试.user.ini 抓包修改将.user.ini修改为jpg图片 在上传一个123.jpg 用蚁剑连接,得到flag...

SkyWalking 10.2.0 SWCK 配置过程
SkyWalking 10.2.0 & SWCK 配置过程 skywalking oap-server & ui 使用Docker安装在K8S集群以外,K8S集群中的微服务使用initContainer按命名空间将skywalking-java-agent注入到业务容器中。 SWCK有整套的解决方案,全安装在K8S群集中。 具体可参…...

iOS 26 携众系统重磅更新,但“苹果智能”仍与国行无缘
美国西海岸的夏天,再次被苹果点燃。一年一度的全球开发者大会 WWDC25 如期而至,这不仅是开发者的盛宴,更是全球数亿苹果用户翘首以盼的科技春晚。今年,苹果依旧为我们带来了全家桶式的系统更新,包括 iOS 26、iPadOS 26…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(二)
HoST框架核心实现方法详解 - 论文深度解读(第二部分) 《Learning Humanoid Standing-up Control across Diverse Postures》 系列文章: 论文深度解读 + 算法与代码分析(二) 作者机构: 上海AI Lab, 上海交通大学, 香港大学, 浙江大学, 香港中文大学 论文主题: 人形机器人…...

<6>-MySQL表的增删查改
目录 一,create(创建表) 二,retrieve(查询表) 1,select列 2,where条件 三,update(更新表) 四,delete(删除表…...

在HarmonyOS ArkTS ArkUI-X 5.0及以上版本中,手势开发全攻略:
在 HarmonyOS 应用开发中,手势交互是连接用户与设备的核心纽带。ArkTS 框架提供了丰富的手势处理能力,既支持点击、长按、拖拽等基础单一手势的精细控制,也能通过多种绑定策略解决父子组件的手势竞争问题。本文将结合官方开发文档,…...

2024年赣州旅游投资集团社会招聘笔试真
2024年赣州旅游投资集团社会招聘笔试真 题 ( 满 分 1 0 0 分 时 间 1 2 0 分 钟 ) 一、单选题(每题只有一个正确答案,答错、不答或多答均不得分) 1.纪要的特点不包括()。 A.概括重点 B.指导传达 C. 客观纪实 D.有言必录 【答案】: D 2.1864年,()预言了电磁波的存在,并指出…...

Leetcode 3577. Count the Number of Computer Unlocking Permutations
Leetcode 3577. Count the Number of Computer Unlocking Permutations 1. 解题思路2. 代码实现 题目链接:3577. Count the Number of Computer Unlocking Permutations 1. 解题思路 这一题其实就是一个脑筋急转弯,要想要能够将所有的电脑解锁&#x…...

OkHttp 中实现断点续传 demo
在 OkHttp 中实现断点续传主要通过以下步骤完成,核心是利用 HTTP 协议的 Range 请求头指定下载范围: 实现原理 Range 请求头:向服务器请求文件的特定字节范围(如 Range: bytes1024-) 本地文件记录:保存已…...
