网络安全RSA加密
网络安全课相关知识:
RSA预备知识
1.1 快速幂算法
顾名思义,快速幂就是快速算底数的$n$次幂。其时间复杂度为${\rm{O(log n)}}$,与朴素的$O\left( n \right)$相比,效率有了极大的提高。具体可以参考百度百科:快速幂。
1.2 扩展欧几里得算法
扩展欧几里得算法(英语:Extended Euclidean algorithm)是欧几里得算法(又叫辗转相除法)的扩展。已知整数a、b,扩展欧几里得算法可以在求得a、b的最大公约数的同时,能找到整数x、y(其中一个很可能是负数),使它们满足贝祖等式
ax+by=gcd(a,b).
ax+by=gcd(a,b).
如果$a$是负数,可以把问题转化成
$\left| a \right|\left( { - x} \right){\rm{ }} + {\rm{ }}by{\rm{ }} = {\rm{ }}gcd\left( {\left| a \right|,b} \right)$($\left| a \right|$为a的绝对值),然后令$x\prime {\rm{ }} = {\rm{ }}\left( { - x} \right)$。具体可以参考维基百科:扩展欧几里得。
1.3 米勒-拉宾素性检验算法
要测试${\rm{N}}$是否为素数,首先将${\rm{N - 1}}$分解为${2^s}d$。在每次测试开始时,先随机选一个介于$[1,N - 1]$的整数$a$,之后如果对所有的$r \in [0,s - 1]$,若${a^d}\bmod N \ne 1$且${a^{{2^r}d}}\bmod N \ne - 1$,则$N$是合数。否则,$N$有$3/4$的概率为素数。
构成该算法的思想是,如果${a^d} \ne 1\left( {{\rm{mod n}}} \right)$以及$n = 1{\rm{ }} + {\rm{ }}{2^s}d$是素数,则值序列
admodn,a2dmodn,a4dmodn,…,a2sdmodn
admodn,a2dmodn,a4dmodn,…,a2sdmodn
将以$1$结束,而且在头一个$1$的前边的值将是$n-1$(当$p$是素数时,对于${y^2} \equiv 1\left( {mod p} \right)$,仅有的解是$y \equiv \pm 1\left( {mod p} \right)$,因为$\left( {y + 1} \right)\left( {y - 1} \right)$必须是$p$的倍数)。注意,如果在该序列中出现了$n-1$,则该序列中的下一个值一定是$1$,因为${\left( {n-1} \right)^2} \equiv {n^2}-2n + 1 \equiv 1\left( {mod n} \right)$。具体可以参考维基百科:米勒-拉宾素性检验。
一、RSA加密简介
RSA加密是一种非对称加密。可以在不直接传递密钥的情况下,完成解密。这能够确保信息的安全性,避免了直接传递密钥所造成的被破解的风险。是由一对密钥来进行加解密的过程,分别称为公钥和私钥。两者之间有数学相关,该加密算法的原理就是对一极大整数做因数分解的困难性来保证安全性。通常个人保存私钥,公钥是公开的(可能同时多人持有)。
二、RSA加密、签名区别
加密和签名都是为了安全性考虑,但略有不同。常有人问加密和签名是用私钥还是公钥?其实都是对加密和签名的作用有所混淆。简单的说,加密是为了防止信息被泄露,而签名是为了防止信息被篡改。这里举2个例子说明。
第一个场景:战场上,B要给A传递一条消息,内容为某一指令。
RSA的加密过程如下:
(1)A生成一对密钥(公钥和私钥),私钥不公开,A自己保留。公钥为公开的,任何人可以获取。
(2)A传递自己的公钥给B,B用A的公钥对消息进行加密。
(3)A接收到B加密的消息,利用A自己的私钥对消息进行解密。
在这个过程中,只有2次传递过程,第一次是A传递公钥给B,第二次是B传递加密消息给A,即使都被敌方截获,也没有危险性,因为只有A的私钥才能对消息进行解密,防止了消息内容的泄露。
第二个场景:A收到B发的消息后,需要进行回复“收到”。
RSA签名的过程如下:
(1)A生成一对密钥(公钥和私钥),私钥不公开,A自己保留。公钥为公开的,任何人可以获取。
(2)A用自己的私钥对消息加签,形成签名,并将加签的消息和消息本身一起传递给B。
(3)B收到消息后,在获取A的公钥进行验签,如果验签出来的内容与消息本身一致,证明消息是A回复的。
在这个过程中,只有2次传递过程,第一次是A传递加签的消息和消息本身给B,第二次是B获取A的公钥,即使都被敌方截获,也没有危险性,因为只有A的私钥才能对消息进行签名,即使知道了消息内容,也无法伪造带签名的回复给B,防止了消息内容的篡改。
但是,综合两个场景你会发现,第一个场景虽然被截获的消息没有泄露,但是可以利用截获的公钥,将假指令进行加密,然后传递给A。第二个场景虽然截获的消息不能被篡改,但是消息的内容可以利用公钥验签来获得,并不能防止泄露。所以在实际应用中,要根据情况使用,也可以同时使用加密和签名,比如A和B都有一套自己的公钥和私钥,当A要给B发送消息时,先用B的公钥对消息加密,再对加密的消息使用A的私钥加签名,达到既不泄露也不被篡改,更能保证消息的安全性。
网络安全学习路线
对于从来没有接触过网络安全的同学,我们帮你准备了详细的学习成长路线图。可以说是最科学最系统的学习路线,大家跟着这个大的方向学习准没问题。
同时每个成长路线对应的板块都有配套的视频提供:

需要网络安全学习路线和视频教程的可以在评论区留言哦~
最后
- 如果你确实想自学的话,我可以把我自己整理收藏的这些教程分享给你,里面不仅有web安全,还有渗透测试等等内容,包含电子书、面试题、pdf文档、视频以及相关的课件笔记,我都已经学过了,都可以免费分享给大家!
给小伙伴们的意见是想清楚,自学网络安全没有捷径,相比而言系统的网络安全是最节省成本的方式,因为能够帮你节省大量的时间和精力成本。坚持住,既然已经走到这条路上,虽然前途看似困难重重,只要咬牙坚持,最终会收到你想要的效果。
黑客工具&SRC技术文档&PDF书籍&web安全等(可分享)


结语
网络安全产业就像一个江湖,各色人等聚集。相对于欧美国家基础扎实(懂加密、会防护、能挖洞、擅工程)的众多名门正派,我国的人才更多的属于旁门左道(很多白帽子可能会不服气),因此在未来的人才培养和建设上,需要调整结构,鼓励更多的人去做“正向”的、结合“业务”与“数据”、“自动化”的“体系、建设”,才能解人才之渴,真正的为社会全面互联网化提供安全保障。
特别声明:
此教程为纯技术分享!本教程的目的决不是为那些怀有不良动机的人提供及技术支持!也不承担因为技术被滥用所产生的连带责任!本教程的目的在于最大限度地唤醒大家对网络安全的重视,并采取相应的安全措施,从而减少由网络安全而带来的经济损失

相关文章:

网络安全RSA加密
网络安全课相关知识: RSA预备知识 1.1 快速幂算法 顾名思义,快速幂就是快速算底数的$n$次幂。其时间复杂度为${\rm{O(log n)}}$,与朴素的$O\left( n \right)$相比,效率有了极大的提高。具体可以参考百度百科:快速幂。…...

Vue学习笔记4
Vue学习笔记 一、自定义创建项目 基于VueCli自定义创建项目架子 二、vuex基本认知 1、vuex概述 是什么:是vue的状态管理工具(插件),状态就是数据 大白话:vuex是一个插件,可以帮助我们管理vue通用的数…...

mariadb数据库的安装与部署
1、通过yum源安装mariadb数据库 yum -y install mariadb-server 2、启动mariadb数据库服务 systemctl start mariadb.service 3、配置mariadb数据库全局环境变量 systemctl enable mariadb.service 4、修改mariadb数据库默认密码,数据库默认密码为空 执行…...

单调队列与栈
一.题 1. 思路: 构建小压大的单调递减栈,对于每个栈的元素都进行处理并加到结果上 class Solution { public:int sumSubarrayMins(vector<int>& arr) {int stk[10000000],top 0;long long ans 0;for(int i 0;i<arr.size();i){while(top…...
)
Matlab 多项式曲线拟合(三维)
文章目录 一、简介二、实现代码三、实现效果参考资料一、简介 对于高维空间曲线的拟合,参数化是一种非常好的方式,可以让我们很容易得到我们想要的目标曲线。 假设给定一组数据点 ( u i , x i ) 、 ( u i ...

机器翻译同样的文本,是从英语翻译成日语更准确还是中文翻译成日语更准确
在大多数情况下,从英语翻译成日语会比从中文翻译成日语更准确,原因如下: 1. 语言结构的相似性 英语和日语的句子结构更接近,特别是在语法、从句使用、定语位置等方面。例如,日语和英语都使用 SVO 结构(主…...

MAC 系统关屏幕后电量消耗极快 Wake Requests
日志为 Wake Requests [*processdasd requestSleepService…info"com.apple.alarm.user-invisible-com.apple.calaccessd… 本人有效方法为: sudo pmset -a hibernatemode 25 sudo pmset -a standby 0 sudo pmset -a autopoweroff 0 会导致hibernatemode 25是…...

golangAPI调用deepseek
目录 1.deepseek官方API调用文档1.访问格式2.curl组装 2.go代码1. config 配置2.模型相关3.错误处理4.deepseekAPI接口实现5. 调用使用 3.响应实例 1.deepseek官方API调用文档 1.访问格式 现在我们来解析这个curl 2.curl组装 // 这是请求头要加的参数-H "Content-Type:…...

提供可传递的易受攻击的依赖项
问题如图所示: 原因:okhttp3.version 3.14.9 版本存在部分漏洞,在 maven 仓库是可以看到的 maven 地址: maven 下图中 Vulnerabilities 即为漏洞 处理:换一个无漏洞的版本即可...

2.14学习记录
Web flag直接读取不就行了? 代码审计: <?php highlight_file(index.php); # 我把flag藏在一个secret文件夹里面了,所以要学会遍历啊~ error_reporting(0); $J1ng $_POST[J]; $Hong $_POST[H]; $Keng $_GET[K]; $Wang $_GET[W]; $d…...
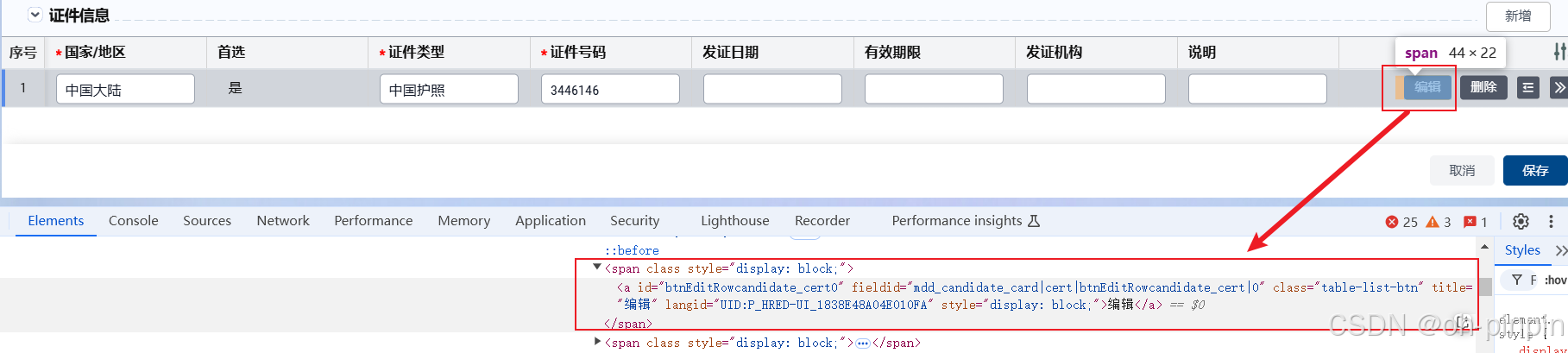
xpath定位--鼠标悬停显示的按钮
UI自动化定位界面元素的过程中,会遇到鼠标悬停才会显示的按钮,鼠标移开就不显示了,无法通过点击它直接定位到元素位置 搜索到这篇文档,办法很好用,特此记录下:chrome调试鼠标悬停后出现的元素_控制台元素调…...

鸿蒙Harmony打包脚本使用整理
最近整理鸿蒙打包相关事宜,遇到很多文档描述不清晰的问题,好在都通过鸿蒙团队的技术支持解决掉了。这里整理一下。 command-line-tools的命令官网基本都有,这里整理几个常用的,还有就是遇到的问题。 hvigorw位置:/comm…...

【C语言】C语言 停车场管理系统的设计与实现(源码)【独一无二】
👉博__主👈:米码收割机 👉技__能👈:C/Python语言 👉专__注👈:专注主流机器人、人工智能等相关领域的开发、测试技术。 系列文章目录 目录 系列文章目录一、设计要求二、设…...

在Autonomous DB中创建训练数据集
在Autonomous DB中创建训练数据集 概述背景步骤解析1. 定义公司术语表2. 使用SQL将数据转换为JSON格式3. 使用SPool命令将SQL查询结果输出为JSON文件4. 查看生成的JSON文件 结果示例结论 概述 在机器学习中,构建高质量的训练数据集是模型成功的关键,尤其…...

Adapting to Length Shift: FlexiLength Network for Trajectory Prediction
概要 轨迹预测在各种应用中发挥着重要作用,包括自动驾驶、机器人技术和场景理解。现有方法通常采用标准化的输入时长,集中于开发紧凑神经网络,以提高在公共数据集上的预测精度。然而,当这些模型在不同观测长度下进行评估时&#…...

张量循环运算:内存溢出原因及解决
写在前面:本博客仅作记录学习之用,部分图片来自网络,如需引用请注明出处,同时如有侵犯您的权益,请联系删除! 文章目录 内存溢出解决方法致谢 内存溢出 使用AlexNet遍历大量图像进行指标运算(LP…...

【Qt】:概述(下载安装、认识 QT Creator)
🌈 个人主页:Zfox_ 🔥 系列专栏:Qt 目录 一:🔥 介绍 🦋 什么是 QT🦋 QT 发展史🦋 Qt版本🦋 QT 优点 一:🔥 搭建Qt开发环境 ǹ…...

11、《Web开发性能优化:静态资源处理与缓存控制深度解析》
Web开发性能优化:静态资源处理与缓存控制深度解析 一、性能优化的核心战场:静态资源处理 现代Web应用静态资源体积占比普遍超过70%,以典型Vue项目为例: dist/ ├─ css/ # 38% 体积 ├─ js/ # 45% 体积 └─ img…...
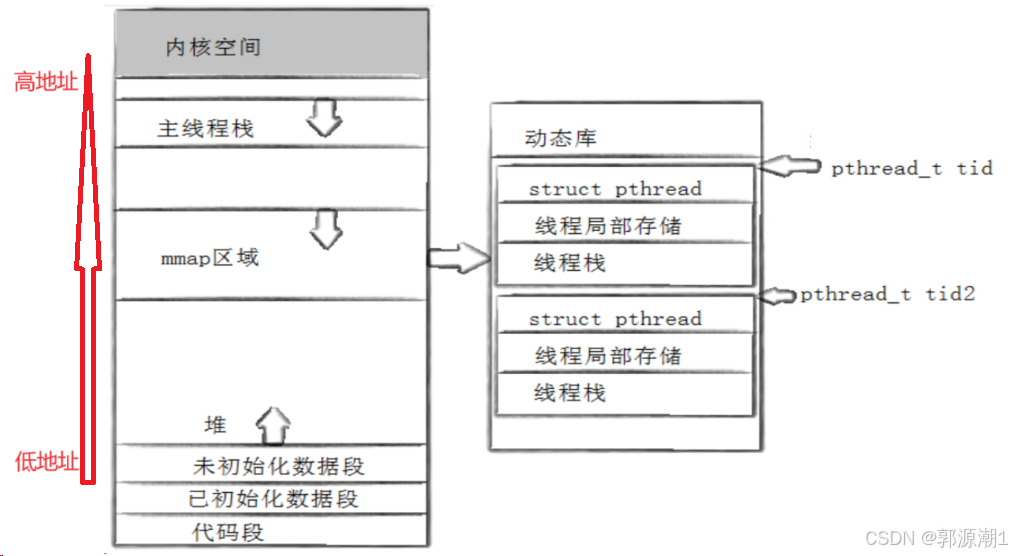
【Linux】多线程 -> 从线程概念到线程控制
线程概念 在一个程序里的一个执行路线就叫做线程(thread)。更准确的定义是:线程是“一个进程内部的控制序列”。一切进程至少都有一个执行线程。线程在进程内部运行,本质是在进程地址空间内运行。在Linux系统中,在CPU眼…...

用什么办法能实现ubuntu里面运行的自己开发的python程序能自动升级。
要实现Ubuntu中自己开发的Python程序自动升级,可以通过以下几种方式: 1. 使用 Git 仓库 定时任务 如果你的Python程序托管在Git仓库中,可以通过定时拉取最新代码来实现自动升级。 步骤: 确保Python程序在Git仓库中。在Ubuntu上…...

多云管理“拦路虎”:深入解析网络互联、身份同步与成本可视化的技术复杂度
一、引言:多云环境的技术复杂性本质 企业采用多云策略已从技术选型升维至生存刚需。当业务系统分散部署在多个云平台时,基础设施的技术债呈现指数级积累。网络连接、身份认证、成本管理这三大核心挑战相互嵌套:跨云网络构建数据…...
:OpenBCI_GUI:从环境搭建到数据可视化(下))
脑机新手指南(八):OpenBCI_GUI:从环境搭建到数据可视化(下)
一、数据处理与分析实战 (一)实时滤波与参数调整 基础滤波操作 60Hz 工频滤波:勾选界面右侧 “60Hz” 复选框,可有效抑制电网干扰(适用于北美地区,欧洲用户可调整为 50Hz)。 平滑处理&…...

(二)TensorRT-LLM | 模型导出(v0.20.0rc3)
0. 概述 上一节 对安装和使用有个基本介绍。根据这个 issue 的描述,后续 TensorRT-LLM 团队可能更专注于更新和维护 pytorch backend。但 tensorrt backend 作为先前一直开发的工作,其中包含了大量可以学习的地方。本文主要看看它导出模型的部分&#x…...

在 Nginx Stream 层“改写”MQTT ngx_stream_mqtt_filter_module
1、为什么要修改 CONNECT 报文? 多租户隔离:自动为接入设备追加租户前缀,后端按 ClientID 拆分队列。零代码鉴权:将入站用户名替换为 OAuth Access-Token,后端 Broker 统一校验。灰度发布:根据 IP/地理位写…...

spring:实例工厂方法获取bean
spring处理使用静态工厂方法获取bean实例,也可以通过实例工厂方法获取bean实例。 实例工厂方法步骤如下: 定义实例工厂类(Java代码),定义实例工厂(xml),定义调用实例工厂ÿ…...

DIY|Mac 搭建 ESP-IDF 开发环境及编译小智 AI
前一阵子在百度 AI 开发者大会上,看到基于小智 AI DIY 玩具的演示,感觉有点意思,想着自己也来试试。 如果只是想烧录现成的固件,乐鑫官方除了提供了 Windows 版本的 Flash 下载工具 之外,还提供了基于网页版的 ESP LA…...

Psychopy音频的使用
Psychopy音频的使用 本文主要解决以下问题: 指定音频引擎与设备;播放音频文件 本文所使用的环境: Python3.10 numpy2.2.6 psychopy2025.1.1 psychtoolbox3.0.19.14 一、音频配置 Psychopy文档链接为Sound - for audio playback — Psy…...
)
【服务器压力测试】本地PC电脑作为服务器运行时出现卡顿和资源紧张(Windows/Linux)
要让本地PC电脑作为服务器运行时出现卡顿和资源紧张的情况,可以通过以下几种方式模拟或触发: 1. 增加CPU负载 运行大量计算密集型任务,例如: 使用多线程循环执行复杂计算(如数学运算、加密解密等)。运行图…...

【OSG学习笔记】Day 16: 骨骼动画与蒙皮(osgAnimation)
骨骼动画基础 骨骼动画是 3D 计算机图形中常用的技术,它通过以下两个主要组件实现角色动画。 骨骼系统 (Skeleton):由层级结构的骨头组成,类似于人体骨骼蒙皮 (Mesh Skinning):将模型网格顶点绑定到骨骼上,使骨骼移动…...

CRMEB 框架中 PHP 上传扩展开发:涵盖本地上传及阿里云 OSS、腾讯云 COS、七牛云
目前已有本地上传、阿里云OSS上传、腾讯云COS上传、七牛云上传扩展 扩展入口文件 文件目录 crmeb\services\upload\Upload.php namespace crmeb\services\upload;use crmeb\basic\BaseManager; use think\facade\Config;/*** Class Upload* package crmeb\services\upload* …...
