项目BUG
项目BUG
前言
我创作这篇博客的目的是记录学习技术过程中的笔记。希望通过分享自己的学习经历,能够帮助到那些对相关领域感兴趣或者正在学习的人们。
项目BUG
1.低频率信号(100k或 200K以下)可以直接用一根导线焊接出几根导线来分几路,高频率信号只能用功分器来分几路。
2.Matlab滤波器设计。
https://mp.weixin.qq.com/s/6bBaNrBuIL2pVn2yEDM2Rw
https://mp.weixin.qq.com/s/MXIrxv0TaKPU4-AZuL6xPA
3.信号“加窗”的原因——减少泄漏。
https://mp.weixin.qq.com/s/c22XYeraj91MB860_D8Ldw
https://zhuanlan.zhihu.com/p/24318554
4.MATLAB 和 Simulink 在电子系统中的应用。
https://mp.weixin.qq.com/s/ofyJX1PqWioKtjRptjn-MA
5.Simulink中MATLAB Function 模块的输入输出可变大小问题、输入输出为结构体、调用外部函数not supported for code generation、输入输出为枚举、对于 Simulink® 信号、参数或数据存储内存,不能使用元胞数组
https://www.mathworks.com/help/simulink/ug/declare-variable-size-inputs-and-outputs_zh_CN.html
https://ww2.mathworks.cn/help/simulink/ug/create-structures-in-matlab-function-blocks.html
https://www.ilovematlab.cn/thread-603082-1-1.html
https://ww2.mathworks.cn/help/ecoder/ug/enumeration.html
7.器件电源设置
电压设置为典型值 15V -15V
电流设置为正常工作电流的3-4倍
器件技术参数表:

正电压:

负电压:

正常工作下的电流:


如果工作电压和电流偏离技术参数表正常工作电压和电流太大,说明异常
8.时钟同步
在两个时钟不同步的情况下,即使两个信号源都发送100MHz的信号,由于时钟频率不同步,两个信号源的信号会出现相位差和频率差。
相位差:由于时钟不同步,两个信号源的时钟边沿触发时间不一致,导致它们的信号相位存在差异。这意味着两个信号的波形会在时间上发生错位,可能会导致信号的重叠或不完整。
频率差:由于时钟频率不同步,两个信号源的时钟频率会存在微小的差异。这意味着两个信号的周期会略微不同,导致它们的频率不完全匹配。长时间运行下,频率差异可能会导致信号的累积相位偏移

9.几百Khz或更高使用模拟滤波器,几百Khz或更低使用数字滤波器
10.直流电压源如果CV(恒压模式)变成CC(恒流模式),则说明器件短路。

11交流电源的频率为50Hz。
12.两个信号频率为 f1 和 f2 的大周期信号的(包含f1和f2信号的完整周期)频率为1/f1与1/f2的公因数的倒数(有多个但要小于等于f1和f2)。可以计算f1和f2的最大公因数,如果没有(如f1为3和f2为4)则为1。比如说500和1000为500,3和4为1。
等于f1和f2)。可以计算f1和f2的最大公因数,如果没有(如f1为3和f2为4)则为1。比如说500和1000为500,3和4为1。
13.MATLAB中cpsd得到的结果为复数,因为互谱有幅值和相位信息,任一频率下的相位为两个信号的相位差,任一频率下的幅度为两个信号的功率大小。故取其绝对值即可得到互功率谱密度。
相关文章:

项目BUG
项目BUG 前言 我创作这篇博客的目的是记录学习技术过程中的笔记。希望通过分享自己的学习经历,能够帮助到那些对相关领域感兴趣或者正在学习的人们。 项目BUG 1.低频率信号(100k或 200K以下)可以直接用一根导线焊接出几根导线来分几路,高频率信号只能…...

wordpress部署nginx版的
一、通过nginx部署wordpress 1、用yum源安装nginx yum install -y nginx 2、安装php相关软件 前提安装webtatic rpm -Uvh https://mirror.webtatic.com/yum/el7/webtatic-release.rpm 通过yum源安装php相关软件 yum -y install php72w php72w-pdo php72w-mysqlnd php72w…...

【鸿蒙Next】优秀鸿蒙博客集锦
鸿蒙基础开发:多文件压缩上传及断点续传_鸿蒙 断点续传-CSDN博客...

【第2章:神经网络基础与实现——2.1 前馈神经网络的结构与工作原理】
老铁们好!今天我们要来一场长达两万字的超详细技术探险,我会像拆解乐高积木一样把前馈神经网络(Feedforward Neural Network)的每个零件摆在台面上,用最接地气的方式让你彻底搞懂这个深度学习基石的工作原理。准备好了吗?我们开始吧! 第一章:神经网络的 “乐高积木” 1…...

python-leetcode-阶乘后的零
172. 阶乘后的零 - 力扣(LeetCode) class Solution:def trailingZeroes(self, n: int) -> int:count 0while n > 5:n // 5count nreturn count...

Python:学生管理系统(继承性、多态性)。
输出样例如图: 题目内容: 利用继承、多态性等面向对象程序功能编写程序,实现学生管理系统,并包含以下内容: 第一,基类为学生类,并以此派生出本科生类、研究生类。 第二,本科生类包含…...

网络安全RSA加密
网络安全课相关知识: RSA预备知识 1.1 快速幂算法 顾名思义,快速幂就是快速算底数的$n$次幂。其时间复杂度为${\rm{O(log n)}}$,与朴素的$O\left( n \right)$相比,效率有了极大的提高。具体可以参考百度百科:快速幂。…...

Vue学习笔记4
Vue学习笔记 一、自定义创建项目 基于VueCli自定义创建项目架子 二、vuex基本认知 1、vuex概述 是什么:是vue的状态管理工具(插件),状态就是数据 大白话:vuex是一个插件,可以帮助我们管理vue通用的数…...

mariadb数据库的安装与部署
1、通过yum源安装mariadb数据库 yum -y install mariadb-server 2、启动mariadb数据库服务 systemctl start mariadb.service 3、配置mariadb数据库全局环境变量 systemctl enable mariadb.service 4、修改mariadb数据库默认密码,数据库默认密码为空 执行…...

单调队列与栈
一.题 1. 思路: 构建小压大的单调递减栈,对于每个栈的元素都进行处理并加到结果上 class Solution { public:int sumSubarrayMins(vector<int>& arr) {int stk[10000000],top 0;long long ans 0;for(int i 0;i<arr.size();i){while(top…...
)
Matlab 多项式曲线拟合(三维)
文章目录 一、简介二、实现代码三、实现效果参考资料一、简介 对于高维空间曲线的拟合,参数化是一种非常好的方式,可以让我们很容易得到我们想要的目标曲线。 假设给定一组数据点 ( u i , x i ) 、 ( u i ...

机器翻译同样的文本,是从英语翻译成日语更准确还是中文翻译成日语更准确
在大多数情况下,从英语翻译成日语会比从中文翻译成日语更准确,原因如下: 1. 语言结构的相似性 英语和日语的句子结构更接近,特别是在语法、从句使用、定语位置等方面。例如,日语和英语都使用 SVO 结构(主…...

MAC 系统关屏幕后电量消耗极快 Wake Requests
日志为 Wake Requests [*processdasd requestSleepService…info"com.apple.alarm.user-invisible-com.apple.calaccessd… 本人有效方法为: sudo pmset -a hibernatemode 25 sudo pmset -a standby 0 sudo pmset -a autopoweroff 0 会导致hibernatemode 25是…...

golangAPI调用deepseek
目录 1.deepseek官方API调用文档1.访问格式2.curl组装 2.go代码1. config 配置2.模型相关3.错误处理4.deepseekAPI接口实现5. 调用使用 3.响应实例 1.deepseek官方API调用文档 1.访问格式 现在我们来解析这个curl 2.curl组装 // 这是请求头要加的参数-H "Content-Type:…...

提供可传递的易受攻击的依赖项
问题如图所示: 原因:okhttp3.version 3.14.9 版本存在部分漏洞,在 maven 仓库是可以看到的 maven 地址: maven 下图中 Vulnerabilities 即为漏洞 处理:换一个无漏洞的版本即可...

2.14学习记录
Web flag直接读取不就行了? 代码审计: <?php highlight_file(index.php); # 我把flag藏在一个secret文件夹里面了,所以要学会遍历啊~ error_reporting(0); $J1ng $_POST[J]; $Hong $_POST[H]; $Keng $_GET[K]; $Wang $_GET[W]; $d…...
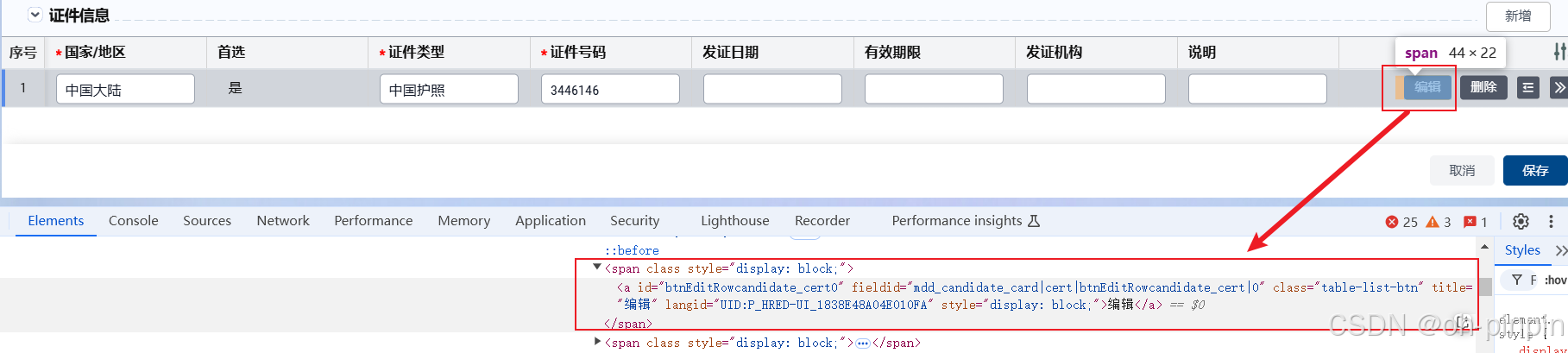
xpath定位--鼠标悬停显示的按钮
UI自动化定位界面元素的过程中,会遇到鼠标悬停才会显示的按钮,鼠标移开就不显示了,无法通过点击它直接定位到元素位置 搜索到这篇文档,办法很好用,特此记录下:chrome调试鼠标悬停后出现的元素_控制台元素调…...

鸿蒙Harmony打包脚本使用整理
最近整理鸿蒙打包相关事宜,遇到很多文档描述不清晰的问题,好在都通过鸿蒙团队的技术支持解决掉了。这里整理一下。 command-line-tools的命令官网基本都有,这里整理几个常用的,还有就是遇到的问题。 hvigorw位置:/comm…...

【C语言】C语言 停车场管理系统的设计与实现(源码)【独一无二】
👉博__主👈:米码收割机 👉技__能👈:C/Python语言 👉专__注👈:专注主流机器人、人工智能等相关领域的开发、测试技术。 系列文章目录 目录 系列文章目录一、设计要求二、设…...

在Autonomous DB中创建训练数据集
在Autonomous DB中创建训练数据集 概述背景步骤解析1. 定义公司术语表2. 使用SQL将数据转换为JSON格式3. 使用SPool命令将SQL查询结果输出为JSON文件4. 查看生成的JSON文件 结果示例结论 概述 在机器学习中,构建高质量的训练数据集是模型成功的关键,尤其…...

模型参数、模型存储精度、参数与显存
模型参数量衡量单位 M:百万(Million) B:十亿(Billion) 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的,但是一个参数所表示多少字节不一定,需要看这个参数以什么…...

大型活动交通拥堵治理的视觉算法应用
大型活动下智慧交通的视觉分析应用 一、背景与挑战 大型活动(如演唱会、马拉松赛事、高考中考等)期间,城市交通面临瞬时人流车流激增、传统摄像头模糊、交通拥堵识别滞后等问题。以演唱会为例,暖城商圈曾因观众集中离场导致周边…...

线程与协程
1. 线程与协程 1.1. “函数调用级别”的切换、上下文切换 1. 函数调用级别的切换 “函数调用级别的切换”是指:像函数调用/返回一样轻量地完成任务切换。 举例说明: 当你在程序中写一个函数调用: funcA() 然后 funcA 执行完后返回&…...

2.Vue编写一个app
1.src中重要的组成 1.1main.ts // 引入createApp用于创建应用 import { createApp } from "vue"; // 引用App根组件 import App from ./App.vue;createApp(App).mount(#app)1.2 App.vue 其中要写三种标签 <template> <!--html--> </template>…...

工程地质软件市场:发展现状、趋势与策略建议
一、引言 在工程建设领域,准确把握地质条件是确保项目顺利推进和安全运营的关键。工程地质软件作为处理、分析、模拟和展示工程地质数据的重要工具,正发挥着日益重要的作用。它凭借强大的数据处理能力、三维建模功能、空间分析工具和可视化展示手段&…...

解决本地部署 SmolVLM2 大语言模型运行 flash-attn 报错
出现的问题 安装 flash-attn 会一直卡在 build 那一步或者运行报错 解决办法 是因为你安装的 flash-attn 版本没有对应上,所以报错,到 https://github.com/Dao-AILab/flash-attention/releases 下载对应版本,cu、torch、cp 的版本一定要对…...

leetcodeSQL解题:3564. 季节性销售分析
leetcodeSQL解题:3564. 季节性销售分析 题目: 表:sales ---------------------- | Column Name | Type | ---------------------- | sale_id | int | | product_id | int | | sale_date | date | | quantity | int | | price | decimal | -…...

Linux --进程控制
本文从以下五个方面来初步认识进程控制: 目录 进程创建 进程终止 进程等待 进程替换 模拟实现一个微型shell 进程创建 在Linux系统中我们可以在一个进程使用系统调用fork()来创建子进程,创建出来的进程就是子进程,原来的进程为父进程。…...

elementUI点击浏览table所选行数据查看文档
项目场景: table按照要求特定的数据变成按钮可以点击 解决方案: <el-table-columnprop"mlname"label"名称"align"center"width"180"><template slot-scope"scope"><el-buttonv-if&qu…...
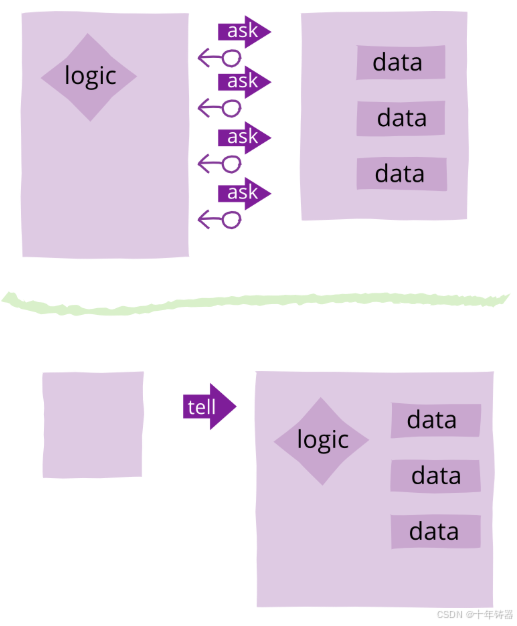
ABAP设计模式之---“Tell, Don’t Ask原则”
“Tell, Don’t Ask”是一种重要的面向对象编程设计原则,它强调的是对象之间如何有效地交流和协作。 1. 什么是 Tell, Don’t Ask 原则? 这个原则的核心思想是: “告诉一个对象该做什么,而不是询问一个对象的状态再对它作出决策。…...
