快速排序
目录
什么是快速排序:
图解:
递归法:
方法一(Hoare法):
代码实现:
思路分析:
方法二(挖坑法):
代码实现:
思路分析:
非递归法:
图解:
代码实现:
思路分析:
快速排序是不稳定的。
什么是快速排序:
任取待排序元素序列中的某元素作为基准值,按照该排序码将待排序集合分割成两子序列,左子序列中所有元素均小于基准值,右子序列中所有元素均大于基准值,然后最左右子序列重复该过程,直到所有元素都排列在相应位置上为止。
图解:

假设 0 下标的数字 3 作为我们的基准值,先看上图的left 和 right ,他们一开始是在start 和 end 的位置。
在走的过程中,right 先走,直到遇到比 3 小的数字停下来,再到 left 走,直到遇到比 3 大的数字停下来;然后交换 此时 left 下标 和 right 下标 的数字,然后不断重复此过程,直到left 与 right 相遇停止;再把最后left 和 right 相遇的 下标位置 与 我们设定的基准值 3 交换;这样就保证了此时的left 位置的下标的左边都是比他小的,右边都是比他大的。也可以说此时的left 下标的数据已经有序了。(用 par 记录left 和 right相遇的位置)
然后,再看此图:

因为使用了 par 记录了 left 和 righjt 相遇的的位置,那么下次划分 一段数据左边则 使用 start 和 par - 1 作为一段新的数据的 left 和 right ,右边 使用 par + 1 和 end 作为一段新的数据的 left 和 right ,不断细分排序重复下去,直到start 与 end 相遇停止划分;看上图绿色椭圆圈出来的start ,那是在 1 下标右边走划分出来的一段,此时start 大于了 end ,也算一种停止划分条件。
所以,停止划分的条件是 start >= end
递归法:
方法一(Hoare法):
代码实现:
public static void quickSortHoare(int[] arr) {quick(arr,0,arr.length - 1);}private static void quick(int[] arr, int start, int end) {if(start >= end) {return;}int par = parrtion(arr,start,end);//往左走quick(arr,start,par - 1);//往右走quick(arr,par + 1,end);}private static int parrtion(int[] arr, int left, int right) {int i = left;int ret = arr[left];while(left < right) {while(left < right && arr[right] >= ret) {right--;}while(left < right && arr[left] <= ret) {left++;}//交换swap(arr,left,right);}//交换swap(arr,i,left);return left;}private static void swap(int[] arr,int i,int j) {int tmp = arr[i];arr[i] = arr[j];arr[j] = tmp;}思路分析:
结合上面我们分析的图解,有个要注意的是 parrtion 方法里 的 left < right && arr[right] >= ret 和 left < right && arr[left] <= ret 这两个的循环条件,前提都要加上 left < right ,因为如果 对于一段已经有序的数据,假设我们使用对一个最小的数据作为基准值,第一个 arr[right] >= ret 循环 判断条件会一直让 right --,如果没有left < right 作为前提条件,会导致 right 越界。
方法二(挖坑法):
代码实现:
public static void quickSort2(int[] arr) {quick(arr,0,arr.length - 1);}private static void quick2(int[] arr, int start, int end) {if(start >= end) {return;}int par = parrtion2(arr,start,end);//往左走quick2(arr,start,par - 1);//往右走quick2(arr,par + 1,end);}private static int parrtion2(int[] arr, int left, int right) {int ret = arr[left];while(left < right) {while(left < right && arr[right] >= ret) {right--;}arr[left] = arr[right];while(left < right && arr[left] <= ret) {left++;}arr[right] = arr[left];}arr[left] = ret;return left;}private static void swap(int[] arr,int i,int j) {int tmp = arr[i];arr[i] = arr[j];arr[j] = tmp;}思路分析:
挖坑法 与 Hoare 法思路很相像,不同的是;
挖坑法 是把 right 找到比 基准值 小的时候,把此时 的 right 下标的值给到 left 下标;left 找到比 基准值 大的时候,把此时 的 left 下标的值给到 right 下标。
最后,由于一开始使用了 ret 存储了基准值,所以当 left 与 right 相遇时把 ret 给到 left 下标的位置。
非递归法:
图解:

快速排序非递归的方法我们借助了一个栈,用来存放数据的下标;
先把一段数据的 left 给到 栈里,再把 right 给到 栈里,然后排完一段序后,得到 par ,再把一段新的数据的 left 和 right 给到 栈里。
要注意,当:

这是分出来的一段数据,当par右边只剩一个元素时,那么右边剩下的一个元素是有序的,par 左边同理。
代码实现:
public static void quickSortNor(int[] arr) {int left = 0;int right = arr.length - 1;int par = parrtion3(arr,left,right);Stack<Integer> stack = new Stack<>();//左边有两个元素及以上if(left + 1 < par) {stack.push(left);stack.push(par - 1);}//右边有两个元素及以上if(par < right - 1) {stack.push(par + 1);stack.push(right);}while(!stack.isEmpty()) {right = stack.pop();left = stack.pop();par = parrtion3(arr,left,right);//左边有两个元素及以上if(left + 1 < par) {stack.push(left);stack.push(par - 1);}//右边有两个元素及以上if(par < right - 1) {stack.push(par + 1);stack.push(right);}}}private static int parrtion3(int[] arr, int left, int right) {int ret = arr[left];while(left < right) {while(left < right && arr[right] >= ret) {right--;}arr[left] = arr[right];while(left < right && arr[left] <= ret) {left++;}arr[right] = arr[left];}arr[left] = ret;return left;}思路分析:
结合上面的图解,一开始在循环外,我们排了一次序,得到了 par ,再把对应的 left 和 right 给到栈里。
当栈不为空时,栈弹出的第一个元素作为相应一段数据 right ,下一个是对应的 left ,原因是我们放入栈时是先 left 再 right;再对其排序后得到新的 par ,再结合图解分析。直到栈为空时结束。
快速排序是不稳定的。
相关文章:

快速排序
目录 什么是快速排序: 图解: 递归法: 方法一(Hoare法): 代码实现: 思路分析: 方法二(挖坑法): 代码实现: 思路分析: 非递…...

国内 ChatGPT Plus/Pro 订阅教程
1. 登录 chat.openai.com 依次点击 Login ,输入邮箱和密码 2. 点击升级 Upgrade 登录自己的 OpenAI 帐户后,点击左下角的 Upgrade to Plus,在弹窗中选择 Upgrade plan。 如果升级入口无法点击,那就访问这个网址,htt…...

易仓科技ai面试
请解释PHP中的面向对象编程的基本概念,并举例说明如何在PHP中定义一个类。 回答思路:需理解类、对象、继承和多态等基本概念,并能通过实例代码展示如何定义类及其属性和方法。 . 类(Class) 类是一个封装了数据和操作…...

LabVIEW用户界面(UI)和用户体验(UX)设计
作为一名 LabVIEW 开发者,满足功能需求、保障使用便捷与灵活只是基础要求。在如今这个用户体验至上的时代,为 LabVIEW 应用程序设计直观且具有美学感的界面,同样是不容忽视的关键任务。一个优秀的界面设计,不仅能提升用户对程序的…...

字玩FontPlayer开发笔记14 Vue3实现多边形工具
目录 字玩FontPlayer开发笔记14 Vue3实现多边形工具笔记整体流程临时变量多边形组件数据结构初始化多边形工具mousedown事件mousemove事件监听mouseup事件渲染控件将多边形转换为平滑的钢笔路径 字玩FontPlayer开发笔记14 Vue3实现多边形工具 字玩FontPlayer是笔者开源的一款字…...

低代码与 Vue.js:技术选型与架构设计
在当下数字化转型的浪潮中,企业对应用开发的效率和质量有着极高的追求。低代码开发平台的兴起,为企业提供了一条快速构建应用的捷径,而 Vue.js 作为热门的前端框架,与低代码开发平台的结合备受关注。如何做好两者的技术选型与架构…...

比较循环与迭代器的性能:Rust 零成本抽象的威力
一、引言 在早期的 I/O 项目中,我们通过对 String 切片的索引和 clone 操作来构造配置结构体,这种方法虽然能确保数据所有权的正确传递,但既显得冗长,又引入了不必要的内存分配。随着对 Rust 迭代器特性的深入了解,我…...

一文了解zookeeper
1.ZooKeeper是什么 简单来说,她是一个分布式的,开放源码的分布式应用程序协调服务 具体来说,他可以做如下事情: 分布式配置管理:ZooKeeper可以存储配置信息,应用程序可以动态读取配置信息。分布式同步&a…...

算法题(67):最长连续序列
审题: 需要我们在O(n)的时间复杂度下找到最长的连续序列长度 思路: 我们可以用两层for循环: 第一层是依次对每个数据遍历,让他们当序列的首元素。 第二层是访问除了该元素的其他元素 但是此时时间复杂度来到…...

大中型企业专用数据安全系统 | 天锐蓝盾终端安全 数据安全
天锐蓝盾系列产品是专门为大中型企业量身定制的数据安全防护产品体系,涵盖天锐蓝盾DLP、天锐蓝盾终端安全管理系统、天锐蓝盾NAC以及其他搭配产品,致力于实现卓越的数据安全防护、施行严格的网络准入控制以及构建稳固的终端安全管理体系。通过全方位的防…...

Deepseek解读 | UE像素流送与实时云渲染技术的差别
为了实现UE引擎开发的3D/XR程序推流,绝大多数开发者会研究像素流送(Pixel Streaming)的使用方法,并尝试将插件集成在程序中。对于短时、少并发、演示场景而言,像素流送可以满足基本需求。当3D/XR项目进入落地交付周期后…...

CTFSHOW-WEB入门-PHP特性109-115
题目:web 109 1. 题目: 2. 解题思路:题目要求获得两个参数,v1 v2,if语句中的意思是要求两个参数都包含字母,条件满足的话,执行 echo new 类名(方法()…...

模糊综合评价法:原理、步骤与MATLAB实现
引言 在复杂决策场景中,评价对象往往涉及多个相互关联的模糊因素。模糊综合评价法通过建立模糊关系矩阵,结合权重分配与合成算子,实现对多因素系统的科学评价。本文详细讲解模糊综合评价法的数学原理、操作步骤,并辅以MATLAB代码…...
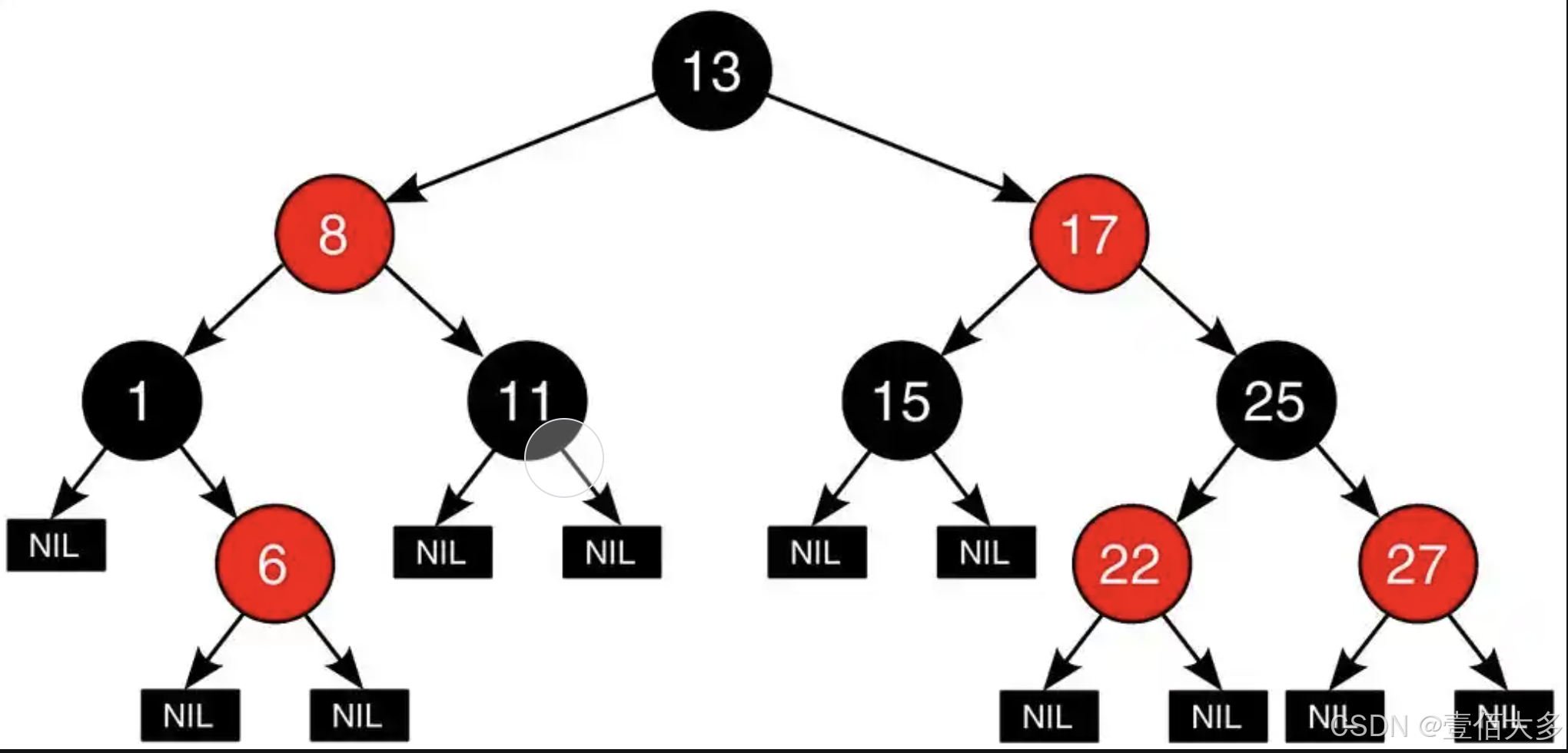
【数据结构-红黑树】
文章目录 红黑树红黑树介绍红黑树的五个基本性质红黑树的平衡原理红黑树的操作红黑树的操作 代码实现节点实现插入和查询操作 红黑树 红黑树介绍 红黑树(Red-Black Tree)是一种自平衡的二叉查找树(Binary Search Tree, BST)&…...

【STM32】舵机SG90
1.舵机原理 舵机内部有一个电位器,当转轴随电机旋转,电位器的电压会发生改变,电压会带动转一定的角度,舵机中的控制板就会电位器输出的电压所代表的角度,与输入的PWM所代表的角度进行比较,从而得出一个旋转…...

【Linux】Socket编程—TCP
🔥 个人主页:大耳朵土土垚 🔥 所属专栏:Linux系统编程 这里将会不定期更新有关Linux的内容,欢迎大家点赞,收藏,评论🥳🥳🎉🎉🎉 文章目…...

c++11 for auto不定参数
数量不定的模板参数。参数分为一个和一包两部分。 冒号的左边声明一个变量。右手边必须是一个容器。从容器(某种数据结构)中找出每一个元素设置到左边这个变量。11之前可以用容器的迭代器去取数据。或者标准库里的foreach...

C#+redis实现消息队列的发布订阅功能
代码 参考c#redis stream实现消息队列以及ack机制文章的思路,实现 SubscribeAttribute.cs using System;namespace DotnetQueue.Attributes {/// <summary>/// 订阅特性/// </summary>[AttributeUsage(AttributeTargets.Method, Inherited false)]pu…...

Docker容器基本操作
容器的基本操作 操作命令(全)命令(简)容器的创建docker container run <image name>docker run <image name>容器的列出(up)docker container lsdocker ps容器的列出(up和exit&…...

从无序到有序:上北智信通过深度数据分析改善会议室资源配置
当前企业普遍面临会议室资源管理难题,预约机制不完善和临时会议多导致资源调度不合理,既有空置又有过度拥挤现象。 针对上述问题,上北智信采用了专业数据分析手段,巧妙融合楼层平面图、环形图、折线图和柱形图等多种可视化工具&a…...

conda相比python好处
Conda 作为 Python 的环境和包管理工具,相比原生 Python 生态(如 pip 虚拟环境)有许多独特优势,尤其在多项目管理、依赖处理和跨平台兼容性等方面表现更优。以下是 Conda 的核心好处: 一、一站式环境管理:…...

调用支付宝接口响应40004 SYSTEM_ERROR问题排查
在对接支付宝API的时候,遇到了一些问题,记录一下排查过程。 Body:{"datadigital_fincloud_generalsaas_face_certify_initialize_response":{"msg":"Business Failed","code":"40004","sub_msg…...

工业安全零事故的智能守护者:一体化AI智能安防平台
前言: 通过AI视觉技术,为船厂提供全面的安全监控解决方案,涵盖交通违规检测、起重机轨道安全、非法入侵检测、盗窃防范、安全规范执行监控等多个方面,能够实现对应负责人反馈机制,并最终实现数据的统计报表。提升船厂…...

.Net框架,除了EF还有很多很多......
文章目录 1. 引言2. Dapper2.1 概述与设计原理2.2 核心功能与代码示例基本查询多映射查询存储过程调用 2.3 性能优化原理2.4 适用场景 3. NHibernate3.1 概述与架构设计3.2 映射配置示例Fluent映射XML映射 3.3 查询示例HQL查询Criteria APILINQ提供程序 3.4 高级特性3.5 适用场…...

vscode(仍待补充)
写于2025 6.9 主包将加入vscode这个更权威的圈子 vscode的基本使用 侧边栏 vscode还能连接ssh? debug时使用的launch文件 1.task.json {"tasks": [{"type": "cppbuild","label": "C/C: gcc.exe 生成活动文件"…...

有限自动机到正规文法转换器v1.0
1 项目简介 这是一个功能强大的有限自动机(Finite Automaton, FA)到正规文法(Regular Grammar)转换器,它配备了一个直观且完整的图形用户界面,使用户能够轻松地进行操作和观察。该程序基于编译原理中的经典…...
多光源(Multiple Lights))
C++.OpenGL (14/64)多光源(Multiple Lights)
多光源(Multiple Lights) 多光源渲染技术概览 #mermaid-svg-3L5e5gGn76TNh7Lq {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-3L5e5gGn76TNh7Lq .error-icon{fill:#552222;}#mermaid-svg-3L5e5gGn76TNh7Lq .erro…...

深入浅出深度学习基础:从感知机到全连接神经网络的核心原理与应用
文章目录 前言一、感知机 (Perceptron)1.1 基础介绍1.1.1 感知机是什么?1.1.2 感知机的工作原理 1.2 感知机的简单应用:基本逻辑门1.2.1 逻辑与 (Logic AND)1.2.2 逻辑或 (Logic OR)1.2.3 逻辑与非 (Logic NAND) 1.3 感知机的实现1.3.1 简单实现 (基于阈…...

iview框架主题色的应用
1.下载 less要使用3.0.0以下的版本 npm install less2.7.3 npm install less-loader4.0.52./src/config/theme.js文件 module.exports {yellow: {theme-color: #FDCE04},blue: {theme-color: #547CE7} }在sass中使用theme配置的颜色主题,无需引入,直接可…...

HubSpot推出与ChatGPT的深度集成引发兴奋与担忧
上周三,HubSpot宣布已构建与ChatGPT的深度集成,这一消息在HubSpot用户和营销技术观察者中引发了极大的兴奋,但同时也存在一些关于数据安全的担忧。 许多网络声音声称,这对SaaS应用程序和人工智能而言是一场范式转变。 但向任何技…...
