【机器学习】监督学习-决策树-CART(Classification and Regression Tree,分类与回归树)详尽版
CART(Classification and Regression Trees)法
CART(分类与回归树)是一种决策树算法,由 Breiman 等人在 1984 年提出。它用于构建分类树(Classification Tree)或回归树(Regression Tree),以解决分类和回归问题。
1. CART 方法概述
CART 方法的核心思想是通过递归二分(Binary Recursive Partitioning)将数据集划分成两个子集,最终构建一棵树。其目标是:
- 分类任务(Classification Tree):将数据划分成多个类别,并最大化类别的纯度(如基尼指数最小化)。
- 回归任务(Regression Tree):最小化均方误差(MSE),使得每个叶子节点的预测值与真实值尽可能接近。
2. CART 分类树
(1) 目标
给定数据集:
其中 xix_ixi 是特征向量, 是类别标签。CART 分类树的目标是找到一个分裂方式,使得每个叶子节点尽可能纯(即尽可能属于同一类别)。
(2) 纯度衡量
CART 使用基尼指数(Gini Index)来衡量节点的不纯度:
其中:
是类别 k 在数据集 D 中的概率。
- 基尼指数越小,数据越纯。
如果在某个特征 的某个阈值 s 处分裂数据集 D:
则分裂后的基尼指数为:
目标是找到最小化 的特征
和阈值 s。
(3) 生成分类树
- 计算所有可能分裂点的基尼指数,选择最优分裂点。
- 递归进行分裂,直到满足停止条件(如树的最大深度、样本数等)。
- 叶子节点的类别由该节点中样本的多数决定。
3. CART 回归树
(1) 目标
对于回归问题,CART 采用均方误差(MSE)来衡量误差:
其中 yˉ\bar{y}yˉ 是数据集 D 中所有样本的均值。
如果对数据进行分裂:
则分裂后的均方误差为:
目标是找到使 最小的分裂方式。
(2) 生成回归树
- 计算所有可能分裂点的 MSE,选择最优分裂点。
- 递归分裂,直到满足停止条件(如叶子节点的样本数小于某个阈值)。
- 叶子节点的输出是该节点样本的均值。
4. 剪枝(Pruning)
CART 生成的树容易过拟合,因此需要剪枝。常见的剪枝方法包括:
- 预剪枝(Pre-pruning):在树生长过程中设定阈值,如最大深度、最小样本数等,提前停止生长。
- 后剪枝(Post-pruning):先生成完整的树,再用交叉验证进行剪枝,移除对测试误差贡献不大的节点。
CART 采用代价复杂度剪枝(Cost Complexity Pruning, CCP),定义损失函数:
其中:
- R(T) 是训练误差(如基尼指数或 MSE)。
- ∣T∣ 是树的叶子节点个数。
- α 是正则化参数,控制复杂度。
选择最优 α 使得交叉验证误差最小。
5. CART 与其他决策树的对比
| 方法 | 目标函数 | 分裂标准 | 处理类别型变量 | 剪枝 |
|---|---|---|---|---|
| ID3 | 信息增益 | 信息增益最大化 | 不支持 | 无剪枝 |
| C4.5 | 信息增益比 | 信息增益比最大化 | 支持 | 预剪枝 |
| CART | Gini指数(分类)/ MSE(回归) | 最小化基尼指数或 MSE | 需要编码 | 后剪枝 |
- ID3 采用信息增益,但偏向于多值特征。
- C4.5 采用信息增益比,可以处理连续变量和缺失值。
- CART 采用基尼指数/MSE,并支持后剪枝,适用于分类和回归。
6. 实例
(1) CART 分类树
假设我们有如下 4 个样本,每个样本有两个特征 和一个类别标签
:
| 样本编号 | 特征 | 特征 | 类别 |
|---|---|---|---|
| 1 | 2.7 | 4.5 | 0 |
| 2 | 3.4 | 1.8 | 1 |
| 3 | 1.3 | 3.7 | 0 |
| 4 | 5.1 | 2.1 | 1 |
目标:构建 CART 分类树,找到最优特征及分裂点。
步骤 1:计算数据集的基尼指数
CART 采用 基尼指数(Gini Index) 作为分类的纯度衡量指标,其计算公式为:
其中:
是类别 k 在数据集中的比例。
- Gini(D) 越小,数据越纯。
我们计算初始数据集的基尼指数:
- 类别 0(Y=0) 的样本:2 个(样本 1, 3)。
- 类别 1(Y=1) 的样本:2 个(样本 2, 4)。
步骤 2:尝试不同的分裂点
CART 采用 二分法,在所有特征的可能切分点中选择使基尼指数最小的那个。
(1) 选取 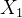 作为分裂特征
作为分裂特征
候选分裂点(取相邻样本的均值):
对每个分裂点计算基尼指数:
① 分裂点 
分裂后:
- 左子集:
→ 样本 {3},类别 {0}
- 右子集:
→ 样本 {1, 2, 4},类别 {0,1,1}
计算基尼指数:
加权基尼指数:
② 分裂点 
分裂后:
- 左子集:
→ 样本 {1, 3},类别 {0, 0}
- 右子集:
→ 样本 {2, 4},类别 {1, 1}
计算基尼指数:
③ 分裂点 
分裂后:
- 左子集:
→ 样本 {1, 2, 3},类别 {0, 1, 0}
- 右子集:
→ 样本 {4},类别 {1}
计算基尼指数:
最优分裂点:,基尼指数最低(0.0)。
步骤 3:递归构建子树
按照 进行分裂,得到:
- 左子树(
):样本 {1, 3},类别全为 0。
- 右子树(
):样本 {2, 4},类别全为 1。
由于子树的类别已纯净,停止分裂。
代码实现
从0开始完整实现
import numpy as np
import matplotlib.pyplot as plt
import matplotlib
import networkx as nxclass Node:def __init__(self, feature=None, threshold=None, left=None, right=None, value=None):self.feature = feature # 选择的特征self.threshold = threshold # 分裂点self.left = left # 左子树self.right = right # 右子树self.value = value # 叶子节点的类别class CARTClassifier:def __init__(self, max_depth=2):self.max_depth = max_depthself.root = Nonedef gini(self, y):"""计算 Gini 系数"""classes, counts = np.unique(y, return_counts=True)p = counts / len(y)return 1 - np.sum(p ** 2)def best_split(self, X, y):"""寻找最佳分裂特征和分裂点"""m, n = X.shapebest_feature, best_threshold, best_gini = None, None, float('inf')best_left_idx, best_right_idx = None, Nonefor feature in range(n):# 排序 X[:, feature] 以便找到最佳分裂点sorted_indices = np.argsort(X[:, feature])sorted_X = X[sorted_indices]sorted_y = y[sorted_indices]for i in range(1, m): # 从1开始,避免最左或最右的分裂if sorted_X[i, feature] == sorted_X[i-1, feature]: # 如果相邻元素相等,跳过continue# 计算分裂点threshold = (sorted_X[i, feature] + sorted_X[i-1, feature]) / 2left_idx = sorted_X[:, feature] <= thresholdright_idx = sorted_X[:, feature] > thresholdleft_gini = self.gini(sorted_y[left_idx])right_gini = self.gini(sorted_y[right_idx])gini_score = (len(left_idx) * left_gini + len(right_idx) * right_gini) / mif gini_score < best_gini:best_feature, best_threshold, best_gini = feature, threshold, gini_scorebest_left_idx, best_right_idx = left_idx, right_idxreturn best_feature, best_threshold, best_left_idx, best_right_idxdef build_tree(self, X, y, depth=0):"""递归构建决策树"""if len(set(y)) == 1 or depth >= self.max_depth:return Node(value=max(set(y), key=list(y).count))feature, threshold, left_idx, right_idx = self.best_split(X, y)if feature is None:return Node(value=max(set(y), key=list(y).count))left_subtree = self.build_tree(X[left_idx], y[left_idx], depth + 1)right_subtree = self.build_tree(X[right_idx], y[right_idx], depth + 1)return Node(feature, threshold, left_subtree, right_subtree)def fit(self, X, y):"""训练分类树"""self.root = self.build_tree(X, y)def predict_one(self, x, node):"""单样本预测"""if node.value is not None:return node.valueif x[node.feature] <= node.threshold:return self.predict_one(x, node.left)else:return self.predict_one(x, node.right)def predict(self, X):"""批量预测"""return np.array([self.predict_one(sample, self.root) for sample in X])def print_tree(self, node=None, depth=0):"""文本格式输出决策树"""if node is None:node = self.rootif node.value is not None:print(" " * depth + f"Leaf: Class {node.value}")returnfeature_name = f"X{node.feature + 1}" # 显示为 X1, X2, ...print(" " * depth + f"|--- {feature_name} <= {node.threshold:.3f}")self.print_tree(node.left, depth + 1)self.print_tree(node.right, depth + 1)def plot_tree(self):"""可视化决策树"""graph = nx.DiGraph()pos = {}def traverse(node, depth=0, x=0, parent=None):if node is None:returnnode_id = id(node)pos[node_id] = (x, -depth)label = f"X[{node.feature}] <= {node.threshold:.2f}" if node.value is None else f"Class {node.value}"graph.add_node(node_id, label=label)if parent is not None:graph.add_edge(parent, node_id)traverse(node.left, depth + 1, x - 2 ** (-depth), node_id)traverse(node.right, depth + 1, x + 2 ** (-depth), node_id)traverse(self.root)labels = nx.get_node_attributes(graph, 'label')plt.figure(figsize=(8, 6))nx.draw(graph, pos, with_labels=True, labels=labels, node_size=2000, node_color="lightblue", font_size=10)plt.title("CART 分类树可视化")plt.show()# 数据集
X = np.array([[2.7, 4.5], [3.4, 1.8], [1.3, 3.7], [5.1, 2.1]])
y = np.array([0, 1, 0, 1]) # 分类标签# 训练分类树
tree = CARTClassifier(max_depth=2)
tree.fit(X, y)# 预测
y_pred = tree.predict(X)
print("预测结果:", y_pred)# 输出树结构
tree.print_tree()# 设置支持中文的字体
matplotlib.rcParams['font.sans-serif'] = ['SimHei'] # 使用黑体
matplotlib.rcParams['axes.unicode_minus'] = False # 解决负号显示问题# 画出分类树
tree.plot_tree()
运行效果
预测结果: [0 1 0 1]
|--- X1 <= 3.050|--- X1 <= 3.050Leaf: Class 0Leaf: Class 1|--- X1 <= 3.200Leaf: Class 0Leaf: Class 1
sklearn实现
import numpy as np
import matplotlib.pyplot as plt
import matplotlib
from sklearn.tree import DecisionTreeClassifier, plot_tree, export_text# 数据集
X = np.array([[2.7, 4.5], [3.4, 1.8], [1.3, 3.7], [5.1, 2.1]])
y = np.array([0, 1, 0, 1]) # 分类标签# 训练 sklearn 的分类树
sklearn_tree = DecisionTreeClassifier(criterion="gini", max_depth=2)
sklearn_tree.fit(X, y)# 预测
y_pred_sklearn = sklearn_tree.predict(X)
print("sklearn 预测结果:", y_pred_sklearn)# 文本格式输出print(export_text(sklearn_tree, feature_names=["X1", "X2"]))# 设置支持中文的字体
matplotlib.rcParams['font.sans-serif'] = ['SimHei'] # 使用黑体
matplotlib.rcParams['axes.unicode_minus'] = False # 解决负号显示问题# 画出分类树
plt.figure(figsize=(8, 6))
plot_tree(sklearn_tree, feature_names=["X1", "X2"], class_names=["0", "1"], filled=True)
plt.title("sklearn 决策树")
plt.show()
运行效果
sklearn 预测结果: [0 1 0 1]
|--- X1 <= 3.05
| |--- class: 0
|--- X1 > 3.05
| |--- class: 1 
总结
- 计算整个数据集的基尼指数(初始为 0.5)。
- 依次尝试所有可能的分裂点,计算基尼指数,选择使基尼指数最小的
作为最优分裂点。
- 递归构建子树:
- 若子集数据的类别已经纯净,则停止分裂。
- 否则继续递归分裂,直到满足终止条件。
最终得到最优的二分决策树,能够对新的数据进行分类。
(2) CART 回归树
假设我们有如下 5 个样本,每个样本有一个特征 X 和对应的目标值 Y:
| 样本编号 | 特征 X | 目标值 Y |
|---|---|---|
| 1 | 1.0 | 2.0 |
| 2 | 2.0 | 2.5 |
| 3 | 3.0 | 4.0 |
| 4 | 4.0 | 4.5 |
| 5 | 5.0 | 5.0 |
目标:构建 CART 回归树,找到最优的分裂点,使得均方误差(MSE)最小。
步骤 1:计算数据集的总方差
回归树使用 均方误差(Mean Squared Error, MSE) 作为分裂标准:
其中:
是数据集的平均目标值。
计算整个数据集的均值:
计算整体均方误差:
步骤 2:尝试不同的分裂点
CART 采用 二分法,在所有可能的分裂点中选择使得 MSE 最小的点。
(1) 选取 X 作为分裂特征
候选分裂点(取相邻样本的均值):
对每个分裂点计算 MSE。
① 分裂点 X=1.5
分裂后:
- 左子集:X ≤ 1.5 → 样本 {1},Y={2.0}Y = \{2.0\}Y={2.0}。
- 右子集:X > 1.5 → 样本 {2, 3, 4, 5},Y={2.5, 4.0, 4.5, 5.0}。
计算左子集 MSE:
(只有一个样本)
计算右子集的均值:
计算右子集 MSE:
加权 MSE:
② 分裂点 X=2.5
分裂后:
- 左子集:X ≤ 2.5 → 样本 {1, 2},Y={2.0, 2.5}。
- 右子集:X > 2.5 → 样本 {3, 4, 5},Y={4.0, 4.5, 5.0}。
计算左子集均值:
计算左子集 MSE:
计算右子集均值:
计算右子集 MSE:
加权 MSE:
步骤 3:选择最优分裂点
- X = 1.5 时
。
- X = 2.5 时
(最小)。
- 其他分裂点的 MSE 更大。
最优分裂点:X = 2.5。
步骤 4:递归构建子树
按照 X = 2.5 进行分裂,得到:
- 左子树(X ≤ 2.5):均值为 2.25。
- 右子树(X > 2.5):均值为 4.5。
由于误差已足够小,停止分裂。
最终的回归树
如果输入新的 X 值:
- 若 X ≤ 2.5,则预测值为 2.25。
- 若 X > 2.5,则预测值为 4.5。
代码实现
从0开始完整实现
import numpy as np
import matplotlib.pyplot as plt
import matplotlib# 定义节点类
class Node:"""回归树节点"""def __init__(self, feature=None, threshold=None, left=None, right=None, value=None):self.feature = feature # 分裂的特征索引(这里只有 1 个特征,固定为 0)self.threshold = threshold # 分裂阈值self.left = left # 左子树self.right = right # 右子树self.value = value # 叶子节点的预测值# 定义 CART 回归树
class CARTRegressionTree:def __init__(self, min_samples_split=2, max_depth=None):self.min_samples_split = min_samples_split # 最小分裂样本数self.max_depth = max_depth # 最大树深self.root = None # 树的根节点def fit(self, X, y):"""训练回归树"""self.root = self._build_tree(X, y, depth=0)def _build_tree(self, X, y, depth):num_samples = X.shape[0]# 如果当前节点所有样本的目标值都相同,则无需继续分裂if len(np.unique(y)) == 1:return Node(value=y[0])# 叶子节点的预测值为当前节点样本目标值的均值leaf_value = np.mean(y)# 如果样本数不足或已达到最大深度,返回叶子节点if num_samples < self.min_samples_split or (self.max_depth is not None and depth >= self.max_depth):return Node(value=leaf_value)# 寻找最佳分裂:返回最佳特征、最佳分裂点以及左右分割的索引best_feature, best_threshold, best_mse, best_left_idx, best_right_idx = self._find_best_split(X, y)# 若没有找到有效的分裂(通常不会发生),返回叶子节点if best_feature is None:return Node(value=leaf_value)# 递归构建左右子树left_subtree = self._build_tree(X[best_left_idx], y[best_left_idx], depth + 1)right_subtree = self._build_tree(X[best_right_idx], y[best_right_idx], depth + 1)return Node(feature=best_feature, threshold=best_threshold, left=left_subtree, right=right_subtree)def _find_best_split(self, X, y):"""遍历所有候选分裂点,找到最优分裂"""best_mse = float("inf")best_feature, best_threshold = None, Nonebest_left_idx, best_right_idx = None, Nonen_features = X.shape[1]# 对每个特征(这里只有 1 个特征)for feature in range(n_features):# 取该特征上的所有唯一值并排序unique_vals = np.sort(np.unique(X[:, feature]))# 如果唯一值个数不足 2,则无法分裂if unique_vals.shape[0] < 2:continue# 候选分裂点:相邻唯一值的中点candidate_thresholds = (unique_vals[:-1] + unique_vals[1:]) / 2.0for threshold in candidate_thresholds:left_idx = X[:, feature] <= thresholdright_idx = X[:, feature] > threshold# 如果任一侧为空,则跳过if np.sum(left_idx) == 0 or np.sum(right_idx) == 0:continuemse = self._calculate_weighted_mse(y[left_idx], y[right_idx])if mse < best_mse:best_mse = msebest_feature = featurebest_threshold = thresholdbest_left_idx = left_idxbest_right_idx = right_idxreturn best_feature, best_threshold, best_mse, best_left_idx, best_right_idxdef _calculate_weighted_mse(self, y_left, y_right):"""计算左右子集的加权均方误差(这里用 SSE 再除以样本总数)"""def sse(y):mean_y = np.mean(y)return np.sum((y - mean_y) ** 2)left_sse = sse(y_left)right_sse = sse(y_right)total = len(y_left) + len(y_right)return (left_sse + right_sse) / totaldef predict(self, X):"""预测多个样本"""return np.array([self._predict_single(x) for x in X])def _predict_single(self, x):"""单个样本预测"""node = self.rootwhile node.value is None:if x[node.feature] <= node.threshold:node = node.leftelse:node = node.rightreturn node.valuedef print_tree(self, node=None, depth=0):"""以文本格式打印树结构"""if node is None:node = self.rootif node.value is not None:print(" " * depth + f"Leaf: {node.value:.2f}")returnprint(" " * depth + f"X[{node.feature}] <= {node.threshold:.2f}")self.print_tree(node.left, depth + 1)self.print_tree(node.right, depth + 1)# ----------------------------
# 测试代码
# 数据集
X = np.array([[1], [2], [3], [4], [5]])
y = np.array([2.0, 2.5, 4.0, 4.5, 5.0])# 训练从零实现的 CART 回归树(最大深度设为2)
tree = CARTRegressionTree(max_depth=2)
tree.fit(X, y)# 打印树结构,输出应为:
# X[0] <= 2.50
# X[0] <= 1.50
# Leaf: 2.00
# Leaf: 2.50
# X[0] <= 3.50
# Leaf: 4.00
# Leaf: 4.75
tree.print_tree()# 生成预测数据
X_test = np.linspace(0, 6, 10).reshape(-1, 1)
y_pred = tree.predict(X_test)# 可视化
matplotlib.rcParams['font.sans-serif'] = ['SimHei']
matplotlib.rcParams['axes.unicode_minus'] = Falseplt.scatter(X, y, color="red", label="训练数据")
plt.plot(X_test, y_pred, color="blue", label="CART 预测", linewidth=2)
plt.xlabel("X")
plt.ylabel("Y")
plt.title("手写 CART 回归树")
plt.legend()
plt.show()
运行效果
X[0] <= 2.50X[0] <= 1.50Leaf: 2.00Leaf: 2.50X[0] <= 3.50Leaf: 4.00Leaf: 4.75 
sklearn实现
import numpy as np
import matplotlib.pyplot as plt
import matplotlib
from sklearn.tree import DecisionTreeRegressor, export_text# 1. 构造数据集
X = np.array([1, 2, 3, 4, 5]).reshape(-1, 1)
y = np.array([2.0, 2.5, 4.0, 4.5, 5.0])# 2. 训练回归树模型
reg_tree = DecisionTreeRegressor(max_depth=2) # 限制树深度,避免过拟合
reg_tree.fit(X, y)# 3. 生成预测数据
X_test = np.linspace(0, 6, 100).reshape(-1, 1) # 测试数据(0到6之间均匀取100个点)
y_pred = reg_tree.predict(X_test)# 设置支持中文的字体
matplotlib.rcParams['font.sans-serif'] = ['SimHei'] # 使用黑体
matplotlib.rcParams['axes.unicode_minus'] = False # 解决负号显示问题# 4. 可视化结果
print(export_text(reg_tree, feature_names=["X"]))plt.scatter(X, y, color="red", label="训练数据")
plt.plot(X_test, y_pred, color="blue", label="回归树预测", linewidth=2)
plt.xlabel("X")
plt.ylabel("Y")
plt.title("CART 回归树示例")
plt.legend()
plt.show()
运行效果
|--- X <= 2.50
| |--- X <= 1.50
| | |--- value: [2.00]
| |--- X > 1.50
| | |--- value: [2.50]
|--- X > 2.50
| |--- X <= 3.50
| | |--- value: [4.00]
| |--- X > 3.50
| | |--- value: [4.75]
总结
- 计算整个数据集的均方误差。
- 依次尝试所有可能的分裂点,计算 MSE,选择 MSE 最小的分裂点(X = 2.5)。
- 递归构建子树,直到误差足够小。
7. 总结
- CART 是一个用于构建分类树和回归树的决策树算法。
- 采用 基尼指数(分类) 和 MSE(回归) 作为分裂标准。
- 采用 二分法 进行划分,保证树的可解释性。
- 通过 剪枝 避免过拟合,提高泛化能力。
- 相比 ID3 和 C4.5,CART 更适用于数值型数据和回归问题。
相关文章:

【机器学习】监督学习-决策树-CART(Classification and Regression Tree,分类与回归树)详尽版
CART(Classification and Regression Trees)法 CART(分类与回归树)是一种决策树算法,由 Breiman 等人在 1984 年提出。它用于构建分类树(Classification Tree)或回归树(Regression …...

Navicat 迁移数据库 传输数据
Navicat提供的数据传输功能,很好用,可以从一个数据库迁移到另外一个数据库。 步骤:菜单栏----工具—传输—选择源连接和数据库----选择目的地连接和数据库...

Jetpack Compose初体验
入门学习 由于工作需要,我们当前要在老代码的基础上使用 Compose 进行新页面的开发,这项工作主要落在我的身上。因此,我需要先了解 Compose。 这里我入门看的是写给初学者的Jetpack Compose教程,Lazy Layout,有兴趣可…...
-使用ceph-ansible部署实验记录)
ceph部署-14版本(nautilus)-使用ceph-ansible部署实验记录
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言一、环境信息二、部署步骤2.1 基础环境准备2.2 各节点docker环境安装2.3 搭建互信集群2.4 下载ceph-ansible 三、配置部署文件3.1 使用本地docker3.2 配置hosts…...

【C++】C++ 旅馆管理系统(含 源码+报告)【独一无二】
👉博__主👈:米码收割机 👉技__能👈:C/Python语言 👉专__注👈:专注主流机器人、人工智能等相关领域的开发、测试技术。 系列文章目录 目录 系列文章目录一、设计要求二、设…...

快速排序
目录 什么是快速排序: 图解: 递归法: 方法一(Hoare法): 代码实现: 思路分析: 方法二(挖坑法): 代码实现: 思路分析: 非递…...

国内 ChatGPT Plus/Pro 订阅教程
1. 登录 chat.openai.com 依次点击 Login ,输入邮箱和密码 2. 点击升级 Upgrade 登录自己的 OpenAI 帐户后,点击左下角的 Upgrade to Plus,在弹窗中选择 Upgrade plan。 如果升级入口无法点击,那就访问这个网址,htt…...

易仓科技ai面试
请解释PHP中的面向对象编程的基本概念,并举例说明如何在PHP中定义一个类。 回答思路:需理解类、对象、继承和多态等基本概念,并能通过实例代码展示如何定义类及其属性和方法。 . 类(Class) 类是一个封装了数据和操作…...

LabVIEW用户界面(UI)和用户体验(UX)设计
作为一名 LabVIEW 开发者,满足功能需求、保障使用便捷与灵活只是基础要求。在如今这个用户体验至上的时代,为 LabVIEW 应用程序设计直观且具有美学感的界面,同样是不容忽视的关键任务。一个优秀的界面设计,不仅能提升用户对程序的…...

字玩FontPlayer开发笔记14 Vue3实现多边形工具
目录 字玩FontPlayer开发笔记14 Vue3实现多边形工具笔记整体流程临时变量多边形组件数据结构初始化多边形工具mousedown事件mousemove事件监听mouseup事件渲染控件将多边形转换为平滑的钢笔路径 字玩FontPlayer开发笔记14 Vue3实现多边形工具 字玩FontPlayer是笔者开源的一款字…...

低代码与 Vue.js:技术选型与架构设计
在当下数字化转型的浪潮中,企业对应用开发的效率和质量有着极高的追求。低代码开发平台的兴起,为企业提供了一条快速构建应用的捷径,而 Vue.js 作为热门的前端框架,与低代码开发平台的结合备受关注。如何做好两者的技术选型与架构…...

比较循环与迭代器的性能:Rust 零成本抽象的威力
一、引言 在早期的 I/O 项目中,我们通过对 String 切片的索引和 clone 操作来构造配置结构体,这种方法虽然能确保数据所有权的正确传递,但既显得冗长,又引入了不必要的内存分配。随着对 Rust 迭代器特性的深入了解,我…...

一文了解zookeeper
1.ZooKeeper是什么 简单来说,她是一个分布式的,开放源码的分布式应用程序协调服务 具体来说,他可以做如下事情: 分布式配置管理:ZooKeeper可以存储配置信息,应用程序可以动态读取配置信息。分布式同步&a…...

算法题(67):最长连续序列
审题: 需要我们在O(n)的时间复杂度下找到最长的连续序列长度 思路: 我们可以用两层for循环: 第一层是依次对每个数据遍历,让他们当序列的首元素。 第二层是访问除了该元素的其他元素 但是此时时间复杂度来到…...

大中型企业专用数据安全系统 | 天锐蓝盾终端安全 数据安全
天锐蓝盾系列产品是专门为大中型企业量身定制的数据安全防护产品体系,涵盖天锐蓝盾DLP、天锐蓝盾终端安全管理系统、天锐蓝盾NAC以及其他搭配产品,致力于实现卓越的数据安全防护、施行严格的网络准入控制以及构建稳固的终端安全管理体系。通过全方位的防…...

Deepseek解读 | UE像素流送与实时云渲染技术的差别
为了实现UE引擎开发的3D/XR程序推流,绝大多数开发者会研究像素流送(Pixel Streaming)的使用方法,并尝试将插件集成在程序中。对于短时、少并发、演示场景而言,像素流送可以满足基本需求。当3D/XR项目进入落地交付周期后…...

CTFSHOW-WEB入门-PHP特性109-115
题目:web 109 1. 题目: 2. 解题思路:题目要求获得两个参数,v1 v2,if语句中的意思是要求两个参数都包含字母,条件满足的话,执行 echo new 类名(方法()…...

模糊综合评价法:原理、步骤与MATLAB实现
引言 在复杂决策场景中,评价对象往往涉及多个相互关联的模糊因素。模糊综合评价法通过建立模糊关系矩阵,结合权重分配与合成算子,实现对多因素系统的科学评价。本文详细讲解模糊综合评价法的数学原理、操作步骤,并辅以MATLAB代码…...
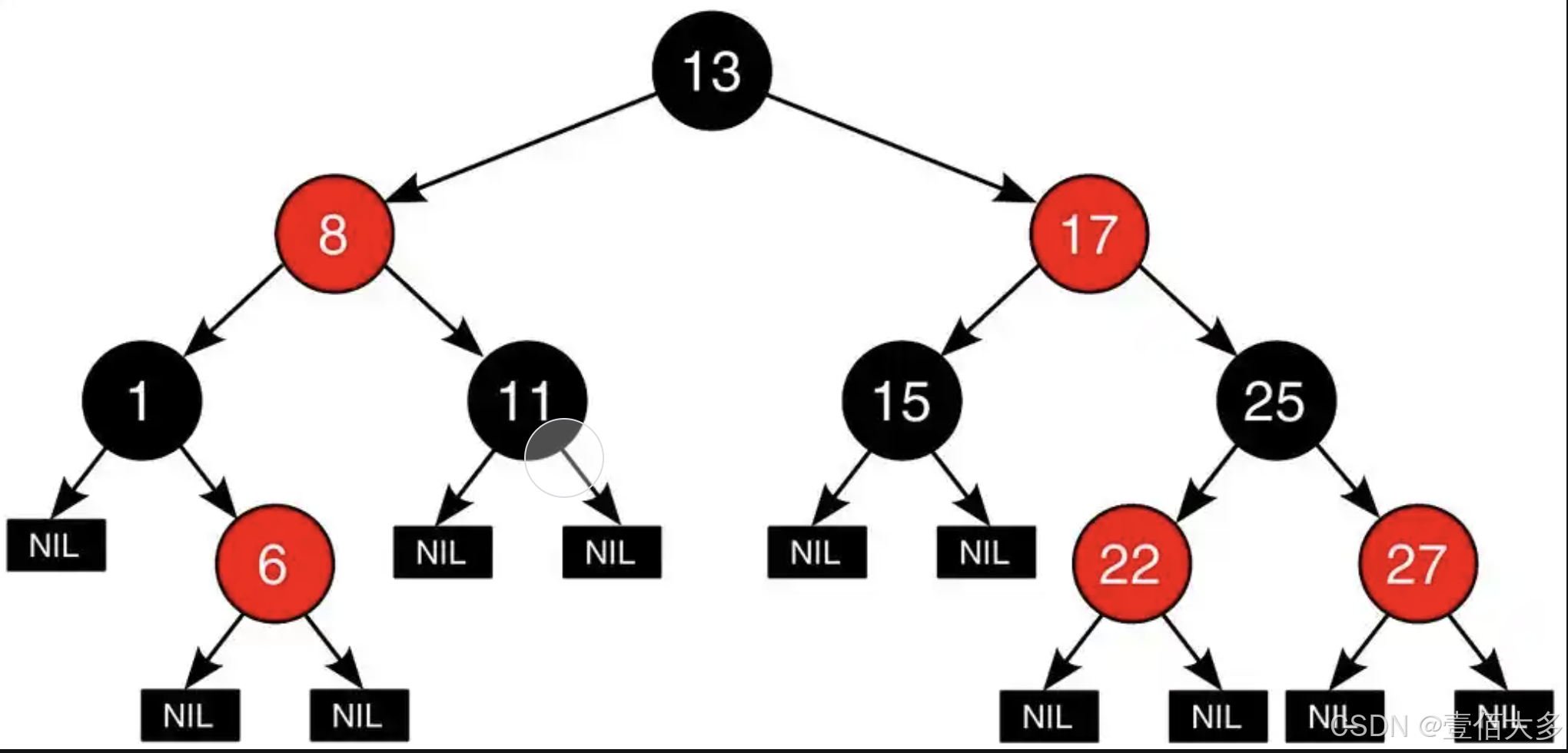
【数据结构-红黑树】
文章目录 红黑树红黑树介绍红黑树的五个基本性质红黑树的平衡原理红黑树的操作红黑树的操作 代码实现节点实现插入和查询操作 红黑树 红黑树介绍 红黑树(Red-Black Tree)是一种自平衡的二叉查找树(Binary Search Tree, BST)&…...

【STM32】舵机SG90
1.舵机原理 舵机内部有一个电位器,当转轴随电机旋转,电位器的电压会发生改变,电压会带动转一定的角度,舵机中的控制板就会电位器输出的电压所代表的角度,与输入的PWM所代表的角度进行比较,从而得出一个旋转…...

conda相比python好处
Conda 作为 Python 的环境和包管理工具,相比原生 Python 生态(如 pip 虚拟环境)有许多独特优势,尤其在多项目管理、依赖处理和跨平台兼容性等方面表现更优。以下是 Conda 的核心好处: 一、一站式环境管理:…...

简易版抽奖活动的设计技术方案
1.前言 本技术方案旨在设计一套完整且可靠的抽奖活动逻辑,确保抽奖活动能够公平、公正、公开地进行,同时满足高并发访问、数据安全存储与高效处理等需求,为用户提供流畅的抽奖体验,助力业务顺利开展。本方案将涵盖抽奖活动的整体架构设计、核心流程逻辑、关键功能实现以及…...

【HarmonyOS 5.0】DevEco Testing:鸿蒙应用质量保障的终极武器
——全方位测试解决方案与代码实战 一、工具定位与核心能力 DevEco Testing是HarmonyOS官方推出的一体化测试平台,覆盖应用全生命周期测试需求,主要提供五大核心能力: 测试类型检测目标关键指标功能体验基…...

关于nvm与node.js
1 安装nvm 安装过程中手动修改 nvm的安装路径, 以及修改 通过nvm安装node后正在使用的node的存放目录【这句话可能难以理解,但接着往下看你就了然了】 2 修改nvm中settings.txt文件配置 nvm安装成功后,通常在该文件中会出现以下配置&…...

基于服务器使用 apt 安装、配置 Nginx
🧾 一、查看可安装的 Nginx 版本 首先,你可以运行以下命令查看可用版本: apt-cache madison nginx-core输出示例: nginx-core | 1.18.0-6ubuntu14.6 | http://archive.ubuntu.com/ubuntu focal-updates/main amd64 Packages ng…...

服务器硬防的应用场景都有哪些?
服务器硬防是指一种通过硬件设备层面的安全措施来防御服务器系统受到网络攻击的方式,避免服务器受到各种恶意攻击和网络威胁,那么,服务器硬防通常都会应用在哪些场景当中呢? 硬防服务器中一般会配备入侵检测系统和预防系统&#x…...

[ICLR 2022]How Much Can CLIP Benefit Vision-and-Language Tasks?
论文网址:pdf 英文是纯手打的!论文原文的summarizing and paraphrasing。可能会出现难以避免的拼写错误和语法错误,若有发现欢迎评论指正!文章偏向于笔记,谨慎食用 目录 1. 心得 2. 论文逐段精读 2.1. Abstract 2…...

苍穹外卖--缓存菜品
1.问题说明 用户端小程序展示的菜品数据都是通过查询数据库获得,如果用户端访问量比较大,数据库访问压力随之增大 2.实现思路 通过Redis来缓存菜品数据,减少数据库查询操作。 缓存逻辑分析: ①每个分类下的菜品保持一份缓存数据…...

MySQL用户和授权
开放MySQL白名单 可以通过iptables-save命令确认对应客户端ip是否可以访问MySQL服务: test: # iptables-save | grep 3306 -A mp_srv_whitelist -s 172.16.14.102/32 -p tcp -m tcp --dport 3306 -j ACCEPT -A mp_srv_whitelist -s 172.16.4.16/32 -p tcp -m tcp -…...

在Ubuntu24上采用Wine打开SourceInsight
1. 安装wine sudo apt install wine 2. 安装32位库支持,SourceInsight是32位程序 sudo dpkg --add-architecture i386 sudo apt update sudo apt install wine32:i386 3. 验证安装 wine --version 4. 安装必要的字体和库(解决显示问题) sudo apt install fonts-wqy…...
