2517. 礼盒的最大甜蜜度(Maximum Tastiness of Candy Box)
2517. 礼盒的最大甜蜜度(Maximum Tastiness of Candy Box)
问题描述
给定一个正整数数组 price,其中 price[i] 表示第 i 类糖果的价格,另给定一个正整数 k。商店将 k 类不同糖果组合成礼盒出售。礼盒的甜蜜度是礼盒中任意两种糖果价格绝对差的最小值。
要求我们返回礼盒的最大甜蜜度。
示例
示例 1:
输入:
price = [13,5,1,8,21,2], k = 3
输出:
8
解释:
选出价格分别为 [13, 5, 21] 的三类糖果。礼盒的甜蜜度为 min(|13 - 5|, |13 - 21|, |5 - 21|) = min(8, 8, 16) = 8。
示例 2:
输入:
price = [1,3,1], k = 2
输出:
2
解释:
选出价格分别为 [1, 3] 的两类糖果。礼盒的甜蜜度为 min(|1 - 3|) = min(2) = 2。
示例 3:
输入:
price = [7,7,7,7], k = 2
输出:
0
解释:
从现有的糖果中任选两类糖果,甜蜜度都会是 0。
解题思路
1. 问题分析
我们需要从 price 数组中选择 k 类糖果,这些糖果的甜蜜度是由它们的价格差决定的,而我们需要找到一种选择方法,使得最大甜蜜度尽可能大。
- 甜蜜度的定义:礼盒中任意两种糖果价格的绝对差的最小值。
- 目标:最大化礼盒的最小价格差。
2. 关键观察
- 排序: 将
price数组排序后,糖果的价格差会变得更加规律。因为如果选择相邻的价格差,显然会更小。 - 二分查找: 为了找到最大甜蜜度,我们可以用二分查找来试探不同的甜蜜度,逐渐逼近最优解。
3. 解法步骤
-
排序: 首先对
price数组进行排序,使得选择的糖果价格差最小。 -
二分查找: 设定一个甜蜜度的范围,从
0到price[-1] - price[0]。在此范围内进行二分查找,检查是否可以选出k类糖果,使得它们的最小价格差大于等于当前的mid。 -
贪心选择: 对于每一个候选的甜蜜度
d,我们可以通过贪心算法来选择糖果。遍历价格数组,确保每个新选择的糖果价格与之前选择的糖果价格差不小于d,如果满足条件,则继续选择糖果。
4. 代码实现
from typing import Listclass Solution:def maximumTastiness(self, price: List[int], k: int) -> int:# 辅助函数:判断是否可以选出至少 k 个糖果,且其最小价格差大于等于 ddef f(d: int) -> int:cnt = 1 # 选择第一个糖果pre = price[0] # 上一个选择的糖果的价格for p in price:if p >= pre + d: # 当前糖果价格与前一个糖果价格差 >= dcnt += 1pre = p # 更新上一个选择的糖果return cntprice.sort() # 对价格数组进行排序left = 0 # 二分查找的左边界right = (price[-1] - price[0]) // (k - 1) + 1 # 二分查找的右边界# 二分查找最大甜蜜度while left + 1 < right:mid = (left + right) // 2if f(mid) >= k: # 如果可以选择 k 个糖果,返回 midleft = midelse:right = midreturn left
5. 时间复杂度
- 排序操作的时间复杂度为
O(n log n),其中n是price数组的长度。 - 二分查找的时间复杂度为
O(log(max_price - min_price))。 - 对每一个中间值
mid,我们需要遍历一次price数组,时间复杂度为O(n)。
因此,总的时间复杂度为 O(n log n + n log(max_price - min_price)),其中 n 是糖果数量,max_price - min_price 是糖果价格的范围。
6. 总结
本题通过对糖果价格数组排序,并利用二分查找和贪心策略来最大化糖果礼盒的甜蜜度。这个解法不仅高效,还能通过二分查找不断逼近最优解,从而找到最大的甜蜜度。
相关文章:
)
2517. 礼盒的最大甜蜜度(Maximum Tastiness of Candy Box)
2517. 礼盒的最大甜蜜度(Maximum Tastiness of Candy Box) 问题描述 给定一个正整数数组 price,其中 price[i] 表示第 i 类糖果的价格,另给定一个正整数 k。商店将 k 类不同糖果组合成礼盒出售。礼盒的甜蜜度是礼盒中任意两种糖…...

Golang 的字符编码与 regexp
前言 最近在使用 Golang 的 regexp 对网络流量做正则匹配时,发现有些情况无法正确进行匹配,找到资料发现 regexp 内部以 UTF-8 编码的方式来处理正则表达式,而网络流量是字节序列,由其中的非 UTF-8 字符造成的问题。 我们这里从 G…...

利用ollama 与deepseek r1大模型搭建本地知识库
1.安装运行ollama ollama下载 https://ollama.com/download/windows 验证ollama是否安装成功 ollama --version 访问ollama本地地址: http://localhost:11434/ 出现如下界面 ollama运行模型 ollama run llama3.2 ollama常用操作命令 启动 Ollama 服务…...

Java短信验证功能简单使用
注册登录阿里云官网:https://www.aliyun.com/ 搜索短信服务 自己一步步申请就可以了 开发文档: https://next.api.aliyun.com/api-tools/sdk/Dysmsapi?version2017-05-25&languagejava-tea&tabprimer-doc 1.引入依赖 <dependency>…...

CAS单点登录(第7版)21.可接受的使用政策
如有疑问,请看视频:CAS单点登录(第7版) 可接受的使用政策 概述 可接受的使用政策 CAS 也称为使用条款或 EULA,它允许用户在继续应用程序之前接受使用策略。此功能的生产级部署需要修改流,以便通过外部存…...
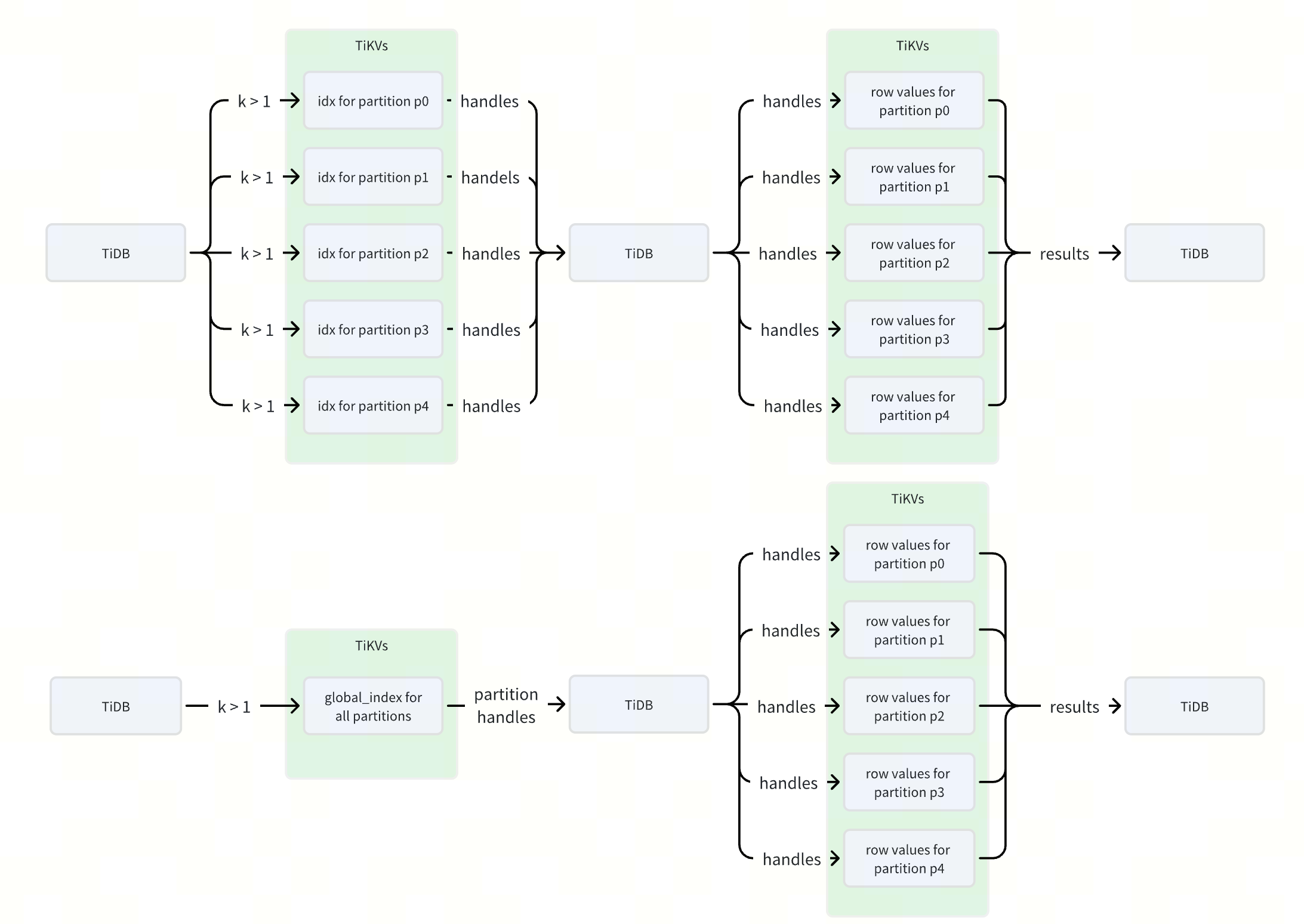
53倍性能提升!TiDB 全局索引如何优化分区表查询?
作者: Defined2014 原文来源: https://tidb.net/blog/7077577f 什么是 TiDB 全局索引 在 TiDB 中,全局索引是一种定义在分区表上的索引类型,它允许索引分区与表分区之间建立一对多的映射关系,即一个索引分区可以对…...

Pythong 解决Pycharm 运行太慢
Pythong 解决Pycharm 运行太慢 官方给Pycharm自身占用的最大内存设低估了限制,我的Pycharm刚开始默认是256mb。 首先找到自己的Pycharm安装目录 根据合适自己的改 保存,重启Pycharm...

库里存储的数据有大量回车时,该如何进行存取
如图,打印模板存了很多坐标性的字段数据: 大量带换行的文本数据存到库里之后取出,前端需要做非空、合法校验, 然后在循环中,使用eval 函数接收每一句字符串,去执行这句 JavaScript 代码。 let arrStr tem…...

【devops】Github Actions Secrets | 如何在Github中设置CI的Secret供CI的yaml使用
一、Github Actions 1、ci.yml name: CIon: [ push ]jobs:build:runs-on: ubuntu-lateststeps:- name: Checkout codeuses: actions/checkoutv3- name: Set up Gouses: actions/setup-gov4with:go-version: 1.23.0- name: Cache Go modulesuses: actions/cachev3with:path: |…...

体验 DeepSeek-R1:解密 1.5B、7B、8B 版本的强大性能与应用
文章目录 🍋引言🍋DeepSeek 模型简介🍋版本更新:1.5B、7B、8B 的区别与特点🍋模型评估🍋体验 DeepSeek 的过程🍋总结 🍋引言 随着大规模语言模型的持续发展,许多模型在性…...

一文说清楚什么是Token以及项目中使用Token延伸的问题
首先可以参考我的往期文章,我这里说清楚了Cookie,Seesion,Token以及JWT是什么 其实Token你就可以理解成这是一个认证令牌就好了 详细分清Session,Cookie和Token之间的区别,以及JWT是什么东西_还分不清 cookie、sessi…...

大模型-Tool call、检索增强
大模型 Tool call 心知天气:https://www.seniverse.com/ 例子:调用天气接口 API from openai import OpenAI import requests import json """ ##### 天气接口 API 密钥获取:https://www.free-api.com/doc/558 ##### &quo…...

【算法】【区间和】acwing算法基础 802. 区间和 【有点复杂,但思路简单】
题目 假定有一个无限长的数轴,数轴上每个坐标上的数都是 0。 现在,我们首先进行 n 次操作,每次操作将某一位置 x 上的数加 c。 接下来,进行 m 次询问,每个询问包含两个整数 l 和 r,你需要求出在区间 [l,r] …...

Ubuntu22.04通过Docker部署Jeecgboot
程序发布环境包括docker、mysql、redis、maven、nodejs、npm等。 一、安装docker 1、用如下命令卸载旧Docker: for pkg in docker.io docker-doc docker-compose docker-compose-v2 podman-docker containerd runc; do sudo apt-get remove $pkg; done 2、安装APT环境依赖包…...

HTML4
HTML 初体验 1.鼠标右键 > 新建 > 文本文档 > 输入以下内容,并保存 2.修改后缀为 .html ,然后双击打开即可 这里的后缀名,使用 .htm 也可以,但推荐使用更标准的 .html <marquee>尚硅谷,让天下没有难…...

STM32F10X 启动文件完整分析
最近在准备面试相关 顺便复盘总结一下之前的内容 启动文件在基于ARM的芯片是很重要的组成部分,它主要负责完成芯片上电启动时的一系列初始化工作和各种异常及中断的入口地址。 也是理解bootloader自举的关键点,所以需要理解一下 1. 向量表定义 启动文件…...

typescript快速入门之安装与运行
安装 安装ts环境,最好全局安装,这样就不需要开一个项目又安装 npm i -g typescript初始化 可以运行初始化配置文件,也可以手动生成;不生成的话会运行默认配置 使用默认配置 把ts文件转成js文件使用的是es3语言,语…...

React源码解读
配置React源码本地调试环境 本次环境构建采用了node版本为16、react-scripts 版本号为 3.4.4,源码下载地址 react源码调试: react源码调试环境 使用 create-react-app 脚手架创建项目 npx create-react-app react-test 进入刚刚下载的目录,弹射 crea…...

【DeepSeek-R1】 API申请(火山方舟联网版)
DeepSeek-R1 API申请(火山方舟联网版) 1、新建联网版应用2、开通信息增强服务3、开启联网内容插件4、创建接入点5、获取模型名称6、获取API Key 如果第一次注册账号,请先按照文章《【Deepseek-R1】 API申请(火山方舟)》…...

负载均衡集群——LVS-DR配置
一、简介 1.1 什么是集群? 两台及以上的计算机完成一个任务的模式称为集群。 常见的集群类型包括: LB(负载均衡)集群:按照不同的算法将前端的访问转发给后端计算点,使节点负载相对平衡。提高并发能力 缺…...

谷歌浏览器插件
项目中有时候会用到插件 sync-cookie-extension1.0.0:开发环境同步测试 cookie 至 localhost,便于本地请求服务携带 cookie 参考地址:https://juejin.cn/post/7139354571712757767 里面有源码下载下来,加在到扩展即可使用FeHelp…...

Go 语言接口详解
Go 语言接口详解 核心概念 接口定义 在 Go 语言中,接口是一种抽象类型,它定义了一组方法的集合: // 定义接口 type Shape interface {Area() float64Perimeter() float64 } 接口实现 Go 接口的实现是隐式的: // 矩形结构体…...

江苏艾立泰跨国资源接力:废料变黄金的绿色供应链革命
在华东塑料包装行业面临限塑令深度调整的背景下,江苏艾立泰以一场跨国资源接力的创新实践,重新定义了绿色供应链的边界。 跨国回收网络:废料变黄金的全球棋局 艾立泰在欧洲、东南亚建立再生塑料回收点,将海外废弃包装箱通过标准…...

ardupilot 开发环境eclipse 中import 缺少C++
目录 文章目录 目录摘要1.修复过程摘要 本节主要解决ardupilot 开发环境eclipse 中import 缺少C++,无法导入ardupilot代码,会引起查看不方便的问题。如下图所示 1.修复过程 0.安装ubuntu 软件中自带的eclipse 1.打开eclipse—Help—install new software 2.在 Work with中…...

C++使用 new 来创建动态数组
问题: 不能使用变量定义数组大小 原因: 这是因为数组在内存中是连续存储的,编译器需要在编译阶段就确定数组的大小,以便正确地分配内存空间。如果允许使用变量来定义数组的大小,那么编译器就无法在编译时确定数组的大…...
)
GitHub 趋势日报 (2025年06月06日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 590 cognee 551 onlook 399 project-based-learning 348 build-your-own-x 320 ne…...

在RK3588上搭建ROS1环境:创建节点与数据可视化实战指南
在RK3588上搭建ROS1环境:创建节点与数据可视化实战指南 背景介绍完整操作步骤1. 创建Docker容器环境2. 验证GUI显示功能3. 安装ROS Noetic4. 配置环境变量5. 创建ROS节点(小球运动模拟)6. 配置RVIZ默认视图7. 创建启动脚本8. 运行可视化系统效果展示与交互技术解析ROS节点通…...

[特殊字符] 手撸 Redis 互斥锁那些坑
📖 手撸 Redis 互斥锁那些坑 最近搞业务遇到高并发下同一个 key 的互斥操作,想实现分布式环境下的互斥锁。于是私下顺手手撸了个基于 Redis 的简单互斥锁,也顺便跟 Redisson 的 RLock 机制对比了下,记录一波,别踩我踩过…...

C# winform教程(二)----checkbox
一、作用 提供一个用户选择或者不选的状态,这是一个可以多选的控件。 二、属性 其实功能大差不差,除了特殊的几个外,与button基本相同,所有说几个独有的 checkbox属性 名称内容含义appearance控件外观可以变成按钮形状checkali…...
)
背包问题双雄:01 背包与完全背包详解(Java 实现)
一、背包问题概述 背包问题是动态规划领域的经典问题,其核心在于如何在有限容量的背包中选择物品,使得总价值最大化。根据物品选择规则的不同,主要分为两类: 01 背包:每件物品最多选 1 次(选或不选&#…...
