Java8适配的markdown转换html工具(FlexMark)
坐标地址:
<dependency><groupId>com.vladsch.flexmark</groupId><artifactId>flexmark-all</artifactId><version>0.60.0</version> </dependency>
工具类代码:
import com.vladsch.flexmark.ext.tables.TablesExtension;
import com.vladsch.flexmark.ext.toc.TocExtension;
import com.vladsch.flexmark.html.HtmlRenderer;
import com.vladsch.flexmark.parser.Parser;
import com.vladsch.flexmark.util.ast.Document;
import com.vladsch.flexmark.util.data.MutableDataSet;
import com.vladsch.flexmark.util.misc.Extension;import java.util.Arrays;public class MarkdownUtil {private static MutableDataSet options = new MutableDataSet();private static Parser parser;private static HtmlRenderer renderer;static {options.set(Parser.EXTENSIONS, Arrays.<Extension>asList(TocExtension.create(), TablesExtension.create()));parser = Parser.builder(options).build();renderer = HtmlRenderer.builder(options).build();}public static String markdownToHtml(String md) {Document document = parser.parse(md);return renderer.render(document);}}
工具类测试:
public class Main {public static void main(String[] args) {String markdownContent = "# 一级标题\n" +"## 二级标题\n" +"### 三级标题\n" +"#### 四级标题\n" +"##### 五级标题\n" +"###### 六级标题\n" +"## 段落\n" +"这是一段普通的段落。\n" +"## 列表\n" +"### 无序列表\n" +"- 项目1\n" +"- 项目2\n" +"- 项目3\n" +"### 有序列表\n" +"1. 项目1\n" +"2. 项目2\n" +"3. 项目3\n" +"## 链接\n" +"[百度](https://www.baidu.com)\n" +"## 图片\n" +"\n" +"## 表格\n" +"| 表头1 | 表头2 | 表头3 |\n" +"|-------|-------|-------|\n" +"| 单元格1 | 单元格2 | 单元格3 |\n" +"| 单元格4 | 单元格5 | 单元格6 |";String html = MarkdownUtil.markdownToHtml(markdownContent);System.out.println(html);}
}
输出结果:

相关文章:

Java8适配的markdown转换html工具(FlexMark)
坐标地址: <dependency><groupId>com.vladsch.flexmark</groupId><artifactId>flexmark-all</artifactId><version>0.60.0</version> </dependency> 工具类代码: import com.vladsch.flexmark.ext.tab…...

超全Deepseek资料包,deepseek下载安装部署提示词及本地部署指南介绍
该资料包涵盖了DeepSeek模型的下载、安装、部署以及本地运行的详细指南,适合希望在本地环境中高效运行DeepSeek模型的用户。资料包不仅包括基础的安装步骤,还提供了68G多套独立部署视频教程教程,针对不同硬件配置的模型选择建议,以…...

Postman - Postman 导入 JSON 文件(导入集合或环境变量)
一、Postman 中的 JSON 文件 在 Postman 中导入的 JSON 文件通常是指集合(Collection)或环境变量(Environments) 集合是 Postman 中用于管理 API 请求的一种方式,可以通过导入 JSON 文件来加载一个集合 环境变量是 P…...

傅里叶分析之掐死教程
https://zhuanlan.zhihu.com/p/19763358 要让读者在不看任何数学公式的情况下理解傅里叶分析。 傅里叶分析 不仅仅是一个数学工具,更是一种可以彻底颠覆一个人以前世界观的思维模式。但不幸的是,傅里叶分析的公式看起来太复杂了,所以很多…...

实在智能与宇树科技、云深科技一同获评浙江省“人工智能服务商”、 “数智优品”等荣誉
近日,浙江省经信厅正式公布《2024 年浙江省人工智能应用场景、应用标杆企业、人工智能服务商及 “数智优品” 名单》。 实在智能获评浙江省“人工智能服务商”,核心产品 “实在 Agent 智能体” 入选 “数智优品”。一同获此殊荣的还有宇树科技、云深处科…...

SpringAI系列 - RAG篇(三) - ETL
目录 一、引言二、组件说明三、集成示例一、引言 接下来我们介绍ETL框架,该框架对应我们之前提到的阶段1:ETL,主要负责知识的提取和管理。ETL 框架是检索增强生成(RAG)数据处理的核心,其将原始数据源转换为结构化向量并进行存储,确保数据以最佳格式供 AI 模型检索。 …...

Leetcode2080:区间内查询数字的频率
题目描述: 请你设计一个数据结构,它能求出给定子数组内一个给定值的 频率 。 子数组中一个值的 频率 指的是这个子数组中这个值的出现次数。 请你实现 RangeFreqQuery 类: RangeFreqQuery(int[] arr) 用下标从 0 开始的整数数组 arr 构造…...
)
北斗导航 | 周跳探测算法(matlab源码)
===================================================== github:https://github.com/MichaelBeechan CSDN:https://blog.csdn.net/u011344545 ===================================================== 周跳 1. 高次差法2. 相位减伪距法3. TurboEdit算法(MW+GF组合)4. 多项…...

Nginx实战_高性能Web服务器与反向代理的配置全解
1. 引言 1.1 Nginx简介 Nginx(发音为 “engine-x”)是一款轻量级、高性能的HTTP服务器和反向代理服务器。它以其高并发处理能力和低资源消耗而闻名,广泛应用于互联网企业中。Nginx不仅可以作为静态文件服务器,还可以通过反向代理功能与后端应用服务器协同工作。 1.2 Ngi…...

基于微信小程序的电影院订票选座系统的设计与实现,SSM+Vue+毕业论文+开题报告+任务书+指导搭建视频
本系统包含用户、管理员两个角色。 用户角色:注册登录、查看首页电影信息推荐、查看电影详情并进行收藏预定、查看电影资讯、在线客服、管理个人订单等。 管理员角色:登录后台、管理电影类型、管理放映厅信息、管理电影信息、管理用户信息、管理订单等。…...

MySQL智障离谱问题,删了库确还存在、也不能再创建同名库
1、问题 今天跟后端朋友接毕设单子的时候,后端穿过来的【weather.sql】这个文件没弄好,导致这个【weather】数据库的数据是错的,因此我用datagrip的GUI界面直接右键删除,结果就是tmd删不掉,ok,我只能在那新…...

基于单片机的多功能门铃控制系统设计(论文+源码)
1功能设计 本课题为基于单片机的多功能门铃控制系统设计,主要结合单片机技术,门铃控制技术进行设计,在多功能门铃控制系统的设计中,将其主要的设计功能确定如下: (1)可以实现门铃的基础功能…...

分享8款AI生成PPT的工具!含测评
随着人工智能技术的飞速进步,制作PPT变得愈发便捷,仅需输入主题指令,便能在瞬间获得一份完整的演示文稿。尤其在制作篇幅较长的PPT时,手动编写每一页内容并设计格式和排版,不仅效率低下,而且耗时耗力。 本…...

”无痕模式“真的无痕?
无痕模式(也称为 隐身模式): 不保存浏览历史:当你在无痕模式下浏览网页时,浏览器不会保存你的浏览历史。这意味着关闭无痕窗口后,其他人查看浏览器时看不到你访问过的网页记录。 不保存Cookies:…...

蓝桥杯班级活动
题目描述 小明的老师准备组织一次班级活动。班上一共有 n 名 (n 为偶数) 同学,老师想把所有的同学进行分组,每两名同学一组。为了公平,老师给每名同学随机分配了一个 n 以内的正整数作为 id,第 i 名同学的 id 为 ai。 老师希望通…...

PHP支付宝--转账到支付宝账户
官方参考文档: https://opendocs.alipay.com/open/62987723_alipay.fund.trans.uni.transfer?sceneca56bca529e64125a2786703c6192d41&pathHash66064890 可以使用默认应用,也可以自建新应用,此处以默认应用来讲解【默认应用默认支持…...

2.18寒假
今天在题单中看了搜索。 解析:两个一维数组,用于表示上下左右四个方向的偏移量,分别对应 x 轴和 y 轴的偏移,遍历四个方向(左、右、下、上),对于每个方向,检查目标位置是否未走过&am…...
的集成(二))
Docker 与持续集成 / 持续部署(CI/CD)的集成(二)
五、代码示例与解释 (一)Dockerfile 示例 以下是一个简单的基于 Python Flask 应用的 Dockerfile 示例: # 使用Python 3.10-slim作为基础镜像 FROM python:3.10-slim # 设置工作目录 WORKDIR /app # 复制项目文件到容器内的工作目录 C…...
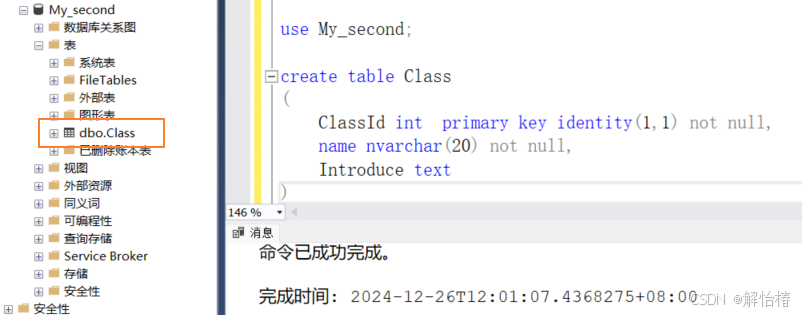
SQL Server的安装和简单使用
目录 一、SQL Server 1.1、简介 1.2、安装包 二、安装SQL Server 2.1、双击安装包 2.2、选择自己想要安装的位置 2.3、点击安装 2.4、安装完成之后会出现以下页面,按照序号依次点击 2.5、不用管密钥,点击下一步 2.6、选择【我接受】 2.7、是否…...
汉诺塔问题)
c/c++蓝桥杯经典编程题100道(19)汉诺塔问题
汉诺塔问题 ->返回c/c蓝桥杯经典编程题100道-目录 目录 汉诺塔问题 一、题型解释 二、例题问题描述 三、C语言实现 解法1:递归法(难度★) 解法2:迭代法(难度★★★) 四、C实现 解法1࿱…...

定时器任务——若依源码分析
分析util包下面的工具类schedule utils: ScheduleUtils 是若依中用于与 Quartz 框架交互的工具类,封装了定时任务的 创建、更新、暂停、删除等核心逻辑。 createScheduleJob createScheduleJob 用于将任务注册到 Quartz,先构建任务的 JobD…...
:爬虫完整流程)
Python爬虫(二):爬虫完整流程
爬虫完整流程详解(7大核心步骤实战技巧) 一、爬虫完整工作流程 以下是爬虫开发的完整流程,我将结合具体技术点和实战经验展开说明: 1. 目标分析与前期准备 网站技术分析: 使用浏览器开发者工具(F12&…...
)
python爬虫:Newspaper3k 的详细使用(好用的新闻网站文章抓取和解析的Python库)
更多内容请见: 爬虫和逆向教程-专栏介绍和目录 文章目录 一、Newspaper3k 概述1.1 Newspaper3k 介绍1.2 主要功能1.3 典型应用场景1.4 安装二、基本用法2.2 提取单篇文章的内容2.2 处理多篇文档三、高级选项3.1 自定义配置3.2 分析文章情感四、实战案例4.1 构建新闻摘要聚合器…...

SpringTask-03.入门案例
一.入门案例 启动类: package com.sky;import lombok.extern.slf4j.Slf4j; import org.springframework.boot.SpringApplication; import org.springframework.boot.autoconfigure.SpringBootApplication; import org.springframework.cache.annotation.EnableCach…...

手机平板能效生态设计指令EU 2023/1670标准解读
手机平板能效生态设计指令EU 2023/1670标准解读 以下是针对欧盟《手机和平板电脑生态设计法规》(EU) 2023/1670 的核心解读,综合法规核心要求、最新修正及企业合规要点: 一、法规背景与目标 生效与强制时间 发布于2023年8月31日(OJ公报&…...

标注工具核心架构分析——主窗口的图像显示
🏗️ 标注工具核心架构分析 📋 系统概述 主要有两个核心类,采用经典的 Scene-View 架构模式: 🎯 核心类结构 1. AnnotationScene (QGraphicsScene子类) 主要负责标注场景的管理和交互 🔧 关键函数&…...

[C++错误经验]case语句跳过变量初始化
标题:[C错误经验]case语句跳过变量初始化 水墨不写bug 文章目录 一、错误信息复现二、错误分析三、解决方法 一、错误信息复现 write.cc:80:14: error: jump to case label80 | case 2:| ^ write.cc:76:20: note: crosses initialization…...
claude3.7高阶玩法,生成系统架构图,国内直接使用
文章目录 零、前言一、操作指南操作指导 二、提示词模板三、实战图书管理系统通过4o模型生成系统描述通过claude3.7生成系统架构图svg代码转换成图片 在线考试系统通过4o模型生成系统描述通过claude3.7生成系统架构图svg代码转换成图片 四、感受 零、前言 现在很多AI大模型可以…...

Java求职者面试:微服务技术与源码原理深度解析
Java求职者面试:微服务技术与源码原理深度解析 第一轮:基础概念问题 1. 请解释什么是微服务架构,并说明其优势和挑战。 微服务架构是一种将单体应用拆分为多个小型、独立的服务的软件开发方法。每个服务都运行在自己的进程中,并…...

[electron]预脚本不显示内联script
script-src self 是 Content Security Policy (CSP) 中的一个指令,它的作用是限制加载和执行 JavaScript 脚本的来源。 具体来说: self 表示 当前源。也就是说,只有来自当前网站或者当前页面所在域名的 JavaScript 脚本才被允许执行。"…...
