小哆啦解题记:螺旋矩阵
小哆啦开始刷力扣的第二十八天
54. 螺旋矩阵 - 力扣(LeetCode)
🌪️ 一场螺旋风暴的较量
在一个阳光明媚的午后,小哆啦悠闲地坐在窗边啃着曲奇,突然,一道神秘的光芒闪过,小智从代码的虚空中出现。
“哆啦,我今天带来了一个特别有意思的题目!”小智眨着眼睛说。
“哦?是什么?”小哆啦眯起眼睛,嘴角还沾着饼干屑。
“螺旋矩阵! ”小智一挥手,白板上赫然出现了一道经典题目:
给你一个
m行n列的矩阵matrix,要求你按照顺时针螺旋顺序,返回矩阵中的所有元素。
示例:
输入:matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出:[1,2,3,6,9,8,7,4,5]
“这也太简单了吧!”小哆啦信心满满地说,“让我来个暴力解法!沿着顺时针走一圈不就好了嘛!”
🚀 第一回合:暴力解法上线
小哆啦撸起袖子,啪啪敲起键盘,写下了第一个版本:
function spiralOrder(matrix: number[][]): number[] {if (matrix.length === 0 || matrix[0].length === 0) return [];const m = matrix.length;const n = matrix[0].length;const result: number[] = [];const visited: boolean[][] = Array.from({ length: m }, () => Array(n).fill(false));let direction = 0; // 0: 右, 1: 下, 2: 左, 3: 上let row = 0, col = 0;const directions = [[0, 1], [1, 0], [0, -1], [-1, 0]];for (let i = 0; i < m * n; i++) {result.push(matrix[row][col]);visited[row][col] = true;const nextRow = row + directions[direction][0];const nextCol = col + directions[direction][1];if (nextRow >= 0 && nextRow < m && nextCol >= 0 && nextCol < n && !visited[nextRow][nextCol]) {row = nextRow;col = nextCol;} else {direction = (direction + 1) % 4;row += directions[direction][0];col += directions[direction][1];}}return result;
}
小哆啦按下运行键,屏幕上果然输出了**[1,2,3,6,9,8,7,4,5]**,结果完全正确!
时间复杂度: O(m * n)
空间复杂度: O(m * n)(额外的 visited 数组)
“哈哈哈,我是不是很厉害!”小哆啦得意地转头看向小智。
🌟 小智的灵魂拷问
小智推了推眼镜,嘴角勾起一抹淡淡的微笑:“哆啦,你确定这就是最优解吗?”
小哆啦一愣:“怎么不是?每个元素都访问了一遍,没多走一步啊!”
小智轻敲白板:“可是……你额外用了一个 visited 数组,空间复杂度已经飙到 O(m * n) 了,这不等于背着一大堆行李去爬山吗?”
小哆啦嘴角抽了抽:“那……那怎么改?”
⚡ 第二回合:边界收缩法登场
“我们可以巧妙利用边界收缩法,”小智耐心地解释道,“动态调整上下左右的边界来控制遍历路径,而不是额外用空间去标记访问过的格子。”
小哆啦听完恍然大悟:“等于说,我们把访问过的路径‘挤压’成边界,把矩阵变成一个收缩的战场!”
于是,在小智的引导下,小哆啦写出了第二版代码:
function spiralOrderOptimized(matrix: number[][]): number[] {if (matrix.length === 0 || matrix[0].length === 0) return [];let top = 0, bottom = matrix.length - 1;let left = 0, right = matrix[0].length - 1;const result: number[] = [];while (top <= bottom && left <= right) {for (let i = left; i <= right; i++) result.push(matrix[top][i]); // 从左到右top++;for (let i = top; i <= bottom; i++) result.push(matrix[i][right]); // 从上到下right--;if (top <= bottom) { // 防止重复遍历for (let i = right; i >= left; i--) result.push(matrix[bottom][i]); // 从右到左bottom--;}if (left <= right) { // 防止重复遍历for (let i = bottom; i >= top; i--) result.push(matrix[i][left]); // 从下到上left++;}}return result;
}
时间复杂度: O(m * n)
空间复杂度: O(1)
🎯 解法对比
| 解法 | 时间复杂度 | 空间复杂度 | 思路 |
|---|---|---|---|
| 暴力解法 | O(m * n) | O(m * n) | 模拟遍历,记录访问过的路径 |
| 边界收缩法 | O(m * n) | O(1) | 动态调整边界,避免额外空间 |
🎬 最终总结:
小哆啦从初出茅庐的暴力解法,到小智提点后的边界收缩法,这不仅是一次代码的升级,更是一场算法思维的蜕变。螺旋矩阵,看似只是绕圈圈,但真正高效的解法,藏在对边界和路径的精准把控之中。
“下次再有这种题目,我一定一眼就用边界收缩法!”小哆啦挥着拳头说道。
“算法的成长,就是不断突破自己思维边界的过程。”小智微微一笑。
如果你也有更妙的思路,欢迎在评论区和我们一起探讨!✨
相关文章:

小哆啦解题记:螺旋矩阵
小哆啦开始刷力扣的第二十八天 54. 螺旋矩阵 - 力扣(LeetCode) 🌪️ 一场螺旋风暴的较量 在一个阳光明媚的午后,小哆啦悠闲地坐在窗边啃着曲奇,突然,一道神秘的光芒闪过,小智从代码的虚空中出现…...

【C#】委托是什么
在 C# 中,委托(Delegate) 是一种类型安全的函数指针,可以将方法作为参数传递或者保存方法的引用。下面详细介绍一下委托的相关概念和用法: 1. 基本概念 类型安全:委托在声明时会指定方法的返回类型和参数…...

[Lc(2)滑动窗口_1] 长度最小的数组 | 无重复字符的最长子串 | 最大连续1的个数 III | 将 x 减到 0 的最小操作数
目录 1. 长度最小的字数组 题解 代码 ⭕2.无重复字符的最长子串 题解 代码 3.最大连续1的个数 III 题解 代码 4.将 x 减到 0 的最小操作数 题解 代码 1. 长度最小的字数组 题目链接:209.长度最小的字数组 题目分析: 给定一个含有 n 个 正整数 的数组…...

迷你世界脚本玩家接口:Player
玩家接口:Player 彼得兔 更新时间: 2024-07-28 17:49:05 继承自 Actor 具体函数名及描述如下: 序号 函数名 函数描述 1 getAttr(...) 玩家属性获取 2 setAttr(...) 玩家属性设置 3 getHostUin(...) 获取房主uin 4 isMainPlayer(...) …...

三、0-1搭建springboot+vue3前后端分离-springboot整合mybatis plus 之本地安装mysql
一、安装mysql: 官网下载:https://dev.mysql.com/downloads/mysql/?spm5176.28103460.0.0.40f75d27Stx4Xj 网盘分享:http://链接: https://pan.baidu.com/s/1mS_-VxrKAeRL3utBvD64gg?pwd6666 提取码: 6666 复制这段内容后打开百度网盘手机…...

市场趋势解析与交易策略优化
市场趋势解析与交易策略优化 在市场环境不断变化的情况下,理解市场趋势并优化交易策略是交易者稳健发展的关键。通过科学的方法识别市场动向,结合数据分析优化交易方案,可以提高交易效率并降低风险。本文将探讨趋势分析的要点,并介…...

Spring Boot 常用注解全解析:从核心到进阶的实践指南
目录 引言:为什么注解是Spring Boot开发者的“战略武器”? 一、核心启动注解 1.1 应用启动三剑客 二、Web开发注解 2.1 控制器层注解 三、依赖注入注解 3.1 依赖管理矩阵 四、数据访问注解 4.1 JPA核心注解 五、配置管理注解 5.1 配置绑定注解…...

如何优化FFmpeg拉流性能及避坑指南
FFmpeg作为流媒体处理的核心工具,其拉流性能直接影响直播/点播体验。本文从协议优化、硬件加速、网络策略三大维度切入,结合实战案例与高频踩坑点,助你突破性能瓶颈! 一、性能优化进阶:从协议到硬件的全链路调优 协议选…...

基础dp——动态规划
目录 一、什么是动态规划? 二、动态规划的使用步骤 1.状态表示 2.状态转移方程 3.初始化 4.填表顺序 5.返回值 三、试题讲解 1.最小花费爬楼梯 2.下降路径最小和 3.解码方法 一、什么是动态规划? 动态规划(Dynamic Programming&…...

通过微步API接口对单个IP进行查询
import requests import json# 微步API的URL和你的API密钥 API_URL "https://api.threatbook.cn/v3/ip/query" API_KEY "***" # 替换为你的微步API密钥 def query_threatbook(ip):"""查询微步API接口,判断IP是否为可疑"…...

LLM实践——DeepSeek技术报告学习(含实现逻辑梳理)
目录 一些基本概念:deepseek-r1-zerodeepseek-R1deepseek-R1 distill model: DeepSeek官网:https://www.deepseek.com/ 一些基本概念: post-training:旨在优化预训练模型的特定能力,包括任务适配性、安…...

Autojs无线连接vscode方法
1.获得电脑的IP 在电脑的CMD界面输入 ipconfig 然后找到ipv4的那一行,后面的即是你的电脑IP地址 2.打开vscode的autojs服务 安装autojs插件 在vscode界面按下ctrlshiftp 输入autojs 找到 点击 之后打开手机上的autojs 之后输入刚刚电脑上的地址 可以看到vsc…...

第一节:基于Winform框架的串口助手小项目---基础控件使用《C#编程》
本人于2025年3月2号学习C#编程,要学会一门编程语言,一定要有一个或多个项目的经验才能对着这门语言有深入的了解,为了深入了解和记录学习C#的学习过程,此文章作为足迹以此记录,为后期巩固学习以及参考奠定基础。内容涉…...

小红书湖仓架构的跃迁之路
作者:李鹏霖(丁典),小红书-研发工程师,StarRocks Contributor & Apache Impala Committer 本文整理自小红书工程师在 StarRocks 年度峰会上的分享,介绍了小红书自助分析平台中,StarRocks 与 Iceberg 结合后&#x…...

pytorch高可用的设计策略和集成放大各自功能
在使用 PyTorch 编写模型时,为确保模型具备高可用性,可从模型设计、代码质量、训练过程、部署等多个方面采取相应的方法,以下为你详细介绍: 模型设计层面 模块化设计 实现方式:将模型拆分成多个小的、独立的模块,每个模块负责特定的功能。例如,在一个图像分类模型中,可…...

神经网络前向微分和后向微分区别
1. 计算顺序 前向微分(前向模式) 从输入到输出逐层计算:沿计算图的正向顺序(输入层 → 输出层),同时计算函数值和导数。 每一步同步更新导数:每个中间变量的导数随值一起计算,例如&…...

Android 创建一个全局通用的ViewModel
(推荐)使用ViewModelStore 代码示例: class MyApplication : Application(), ViewModelStoreOwner {private val mViewModelStore ViewModelStore()override fun onCreate() {super.onCreate()}override val viewModelStore: ViewModelSto…...

windows 利用nvm 管理node.js 2025最新版
1.首先在下载nvm 下载链接 2. 下载最新版本的nvm 3. 同意协议 注意:选择安装路径 之后一直下一步即可 可以取消勾选 open with Powershell 勾选后它会自动打开Powershell 这里选用cmd 输入以下命令查看是否安装成功 nvm version 查看已经安装的版本 我之前自…...

基于物联网技术的电动车防盗系统设计(论文+源码)
1总体设计 本课题为基于物联网技术的电动车防盗系统,在此将整个系统架构设计如图2.1所示,其采用STM32F103单片机为控制器,通过NEO-6M实现GPS定位功能,通过红外传感器检测电瓶是否离开位,通过Air202 NBIOT模块将当前的数…...
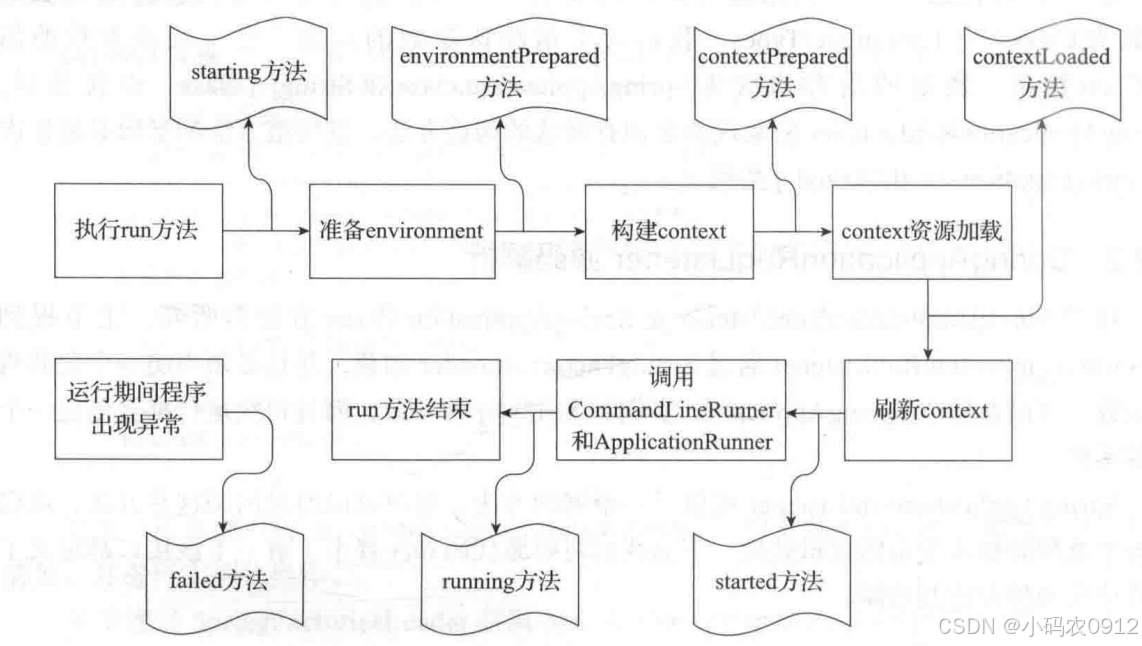
run方法执行过程分析
文章目录 run方法核心流程SpringApplicationRunListener监听器监听器的配置与加载SpringApplicationRunListener源码解析实现类EventPublishingRunListener 初始化ApplicationArguments初始化ConfigurableEnvironment获取或创建环境配置环境 打印BannerSpring应用上下文的创建S…...

黑马Mybatis
Mybatis 表现层:页面展示 业务层:逻辑处理 持久层:持久数据化保存 在这里插入图片描述 Mybatis快速入门 
从WWDC看苹果产品发展的规律
WWDC 是苹果公司一年一度面向全球开发者的盛会,其主题演讲展现了苹果在产品设计、技术路线、用户体验和生态系统构建上的核心理念与演进脉络。我们借助 ChatGPT Deep Research 工具,对过去十年 WWDC 主题演讲内容进行了系统化分析,形成了这份…...

Java 8 Stream API 入门到实践详解
一、告别 for 循环! 传统痛点: Java 8 之前,集合操作离不开冗长的 for 循环和匿名类。例如,过滤列表中的偶数: List<Integer> list Arrays.asList(1, 2, 3, 4, 5); List<Integer> evens new ArrayList…...

Java - Mysql数据类型对应
Mysql数据类型java数据类型备注整型INT/INTEGERint / java.lang.Integer–BIGINTlong/java.lang.Long–––浮点型FLOATfloat/java.lang.FloatDOUBLEdouble/java.lang.Double–DECIMAL/NUMERICjava.math.BigDecimal字符串型CHARjava.lang.String固定长度字符串VARCHARjava.lang…...

使用van-uploader 的UI组件,结合vue2如何实现图片上传组件的封装
以下是基于 vant-ui(适配 Vue2 版本 )实现截图中照片上传预览、删除功能,并封装成可复用组件的完整代码,包含样式和逻辑实现,可直接在 Vue2 项目中使用: 1. 封装的图片上传组件 ImageUploader.vue <te…...

2025盘古石杯决赛【手机取证】
前言 第三届盘古石杯国际电子数据取证大赛决赛 最后一题没有解出来,实在找不到,希望有大佬教一下我。 还有就会议时间,我感觉不是图片时间,因为在电脑看到是其他时间用老会议系统开的会。 手机取证 1、分析鸿蒙手机检材&#x…...
中关于正整数输入的校验规则)
Element Plus 表单(el-form)中关于正整数输入的校验规则
目录 1 单个正整数输入1.1 模板1.2 校验规则 2 两个正整数输入(联动)2.1 模板2.2 校验规则2.3 CSS 1 单个正整数输入 1.1 模板 <el-formref"formRef":model"formData":rules"formRules"label-width"150px"…...

AspectJ 在 Android 中的完整使用指南
一、环境配置(Gradle 7.0 适配) 1. 项目级 build.gradle // 注意:沪江插件已停更,推荐官方兼容方案 buildscript {dependencies {classpath org.aspectj:aspectjtools:1.9.9.1 // AspectJ 工具} } 2. 模块级 build.gradle plu…...

LINUX 69 FTP 客服管理系统 man 5 /etc/vsftpd/vsftpd.conf
FTP 客服管理系统 实现kefu123登录,不允许匿名访问,kefu只能访问/data/kefu目录,不能查看其他目录 创建账号密码 useradd kefu echo 123|passwd -stdin kefu [rootcode caozx26420]# echo 123|passwd --stdin kefu 更改用户 kefu 的密码…...

解读《网络安全法》最新修订,把握网络安全新趋势
《网络安全法》自2017年施行以来,在维护网络空间安全方面发挥了重要作用。但随着网络环境的日益复杂,网络攻击、数据泄露等事件频发,现行法律已难以完全适应新的风险挑战。 2025年3月28日,国家网信办会同相关部门起草了《网络安全…...
